Ensemble de Julia
En dynamique holomorphe, l'ensemble de Julia et l'ensemble de Fatou sont deux ensembles complémentaires l'un de l'autre, définis à partir du comportement d'une fonction (ou d'une application) holomorphe par composition itérée avec elle-même.
.jpg.webp)
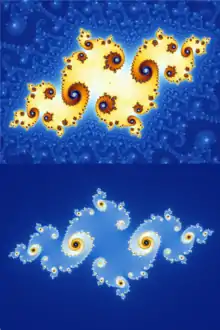
Alors que l'ensemble de Fatou est l'ensemble des points en lesquels un faible changement du point de départ entraîne un faible changement sur la suite de l'itération (stabilité), l'ensemble de Julia est quant à lui, essentiellement caractérisé par le fait qu'une petite perturbation au départ se répercute en un changement radical de cette suite (chaos).
Les ensembles de Julia offrent de nombreux exemples d'ensembles fractals.
Ces deux ensembles ont été nommés en l'honneur des mathématiciens français Pierre Fatou et Gaston Julia dont les travaux, au début du XXe siècle, sont à l'origine d'une nouvelle branche des mathématiques, la dynamique holomorphe.
Si f est la fonction engendrant le système dynamique, on a l'habitude de noter J(f) et F(f) les ensembles de Julia et Fatou qui lui sont associés.
La définition fut initialement donnée pour les fractions rationnelles[1] - [2] - [3] - [4] - [5] - [6] mais on peut l'étendre à d'autres classes de fonctions holomorphes. Les polynômes sont un cas particulier de fractions rationnelles. Pour ces derniers, une autre définition est souvent utilisée : l'ensemble de Julia est la frontière du bassin d'attraction de l'infini. L'équivalence des deux définitions est un théorème. Ci-dessous est présenté un cas particulier de polynôme du second degré.
Un exemple
Étant donnés deux nombres complexes, c et z0, définissons la suite (zn) par la relation de récurrence :
Pour une valeur donnée de c, l'ensemble de Julia correspondant est la frontière de l'ensemble des valeurs initiales z0 pour lesquelles la suite est bornée (l'ensemble de ces valeurs étant, lui, désigné comme l'ensemble de Julia rempli). En déplaçant le point c sur le plan complexe, nous pouvons donc imaginer un film sur lequel nous verrions défiler les ensembles de Julia correspondant aux points c parcourus.
La définition des ensembles de Julia dans ce cas particulier peut être associée à celle de l'ensemble de Mandelbrot qui est l'ensemble de toutes les valeurs de c pour lesquelles la suite (zn) est bornée, en prenant z0 = 0.
L'ensemble de Mandelbrot est un ensemble de paramètres c ayant une propriété particulière pour les ensembles de Julia : en effet, Julia et Fatou ont démontré que pour les points c appartenant à l'ensemble de Mandelbrot, l'ensemble de Julia correspondant est d'« une seule pièce » c'est-à-dire topologiquement connexe, et qu'inversement lorsque le point c traverse la frontière de l'ensemble de Mandelbrot, l'ensemble de Julia se brise en une poussière de Cantor formée de points non connectés mais dont tout voisinage contient un autre point de l'ensemble. Il y a équivalence entre cette propriété et la définition précédente d'un ensemble de Mandelbrot.
Animations
- Ensemble de Julia où c varie sur le cercle unité décalé de 0,25 + 0,5 i.
- Ensemble de Julia où c varie sur une courbe paramétrique.
- Ensemble de Julia où c varie sur un segment.
- Ensemble de Julia où c varie sur le cercle unité.
Images
.png.webp) Ensemble de Julia de z2 + c avec c = 0,3 + 0,5 i.
Ensemble de Julia de z2 + c avec c = 0,3 + 0,5 i..jpg.webp) Ensemble de Julia pour c = 0,285 + 0,01 i (courbes de niveau du nombre d'itérations).
Ensemble de Julia pour c = 0,285 + 0,01 i (courbes de niveau du nombre d'itérations)._II.jpg.webp) Le même ensemble avec une coloration différente (nombre d'itérations et pavage selon le secteur d'arrivée).
Le même ensemble avec une coloration différente (nombre d'itérations et pavage selon le secteur d'arrivée)..jpg.webp) Détail de l'ensemble de Julia pour c = –1,417022285618 + 0,0099534 i.
Détail de l'ensemble de Julia pour c = –1,417022285618 + 0,0099534 i..jpg.webp) Détail de l'ensemble de Julia pour c = –0,038088 + 0.9754633 i.
Détail de l'ensemble de Julia pour c = –0,038088 + 0.9754633 i..jpg.webp) Ensemble de Julia pour c = 0,285 + 0,013 i.
Ensemble de Julia pour c = 0,285 + 0,013 i..jpg.webp) Tracé d'un ensemble de Julia par itération inverse.
Tracé d'un ensemble de Julia par itération inverse. Ensembles de Julia de z2 + c pour différentes valeurs de c.
Ensembles de Julia de z2 + c pour différentes valeurs de c. Ensemble de Julia rempli pour c = 0,285 + 0,01 i.
Ensemble de Julia rempli pour c = 0,285 + 0,01 i. Ensemble de Julia rempli pour c = -1,476.
Ensemble de Julia rempli pour c = -1,476. Ensemble de Julia rempli pour c = −0,4 + 0,6 i.
Ensemble de Julia rempli pour c = −0,4 + 0,6 i. Ensemble de Julia rempli pour c = −0,8+0,156 i.
Ensemble de Julia rempli pour c = −0,8+0,156 i.
Notes et références
- Gaston Julia, « Mémoire sur l'itération des fonctions rationnelles », J. Math. Pures Appl., vol. 8, , p. 47-245 (lire en ligne).
- Pierre Fatou, « Sur les substitutions rationnelles », Comptes Rendus de l'Académie des Sciences de Paris, vol. 164, , p. 806-808 (lire en ligne).
- Fatou 1917, p. 992-995.
- Pierre Fatou, « Sur les équations fonctionnelles », Bull. Soc. Math. Fr., vol. 47, , p. 161-271 (lire en ligne).
- Pierre Fatou, « Sur les équations fonctionnelles », Bull. Soc. Math. Fr., vol. 48, , p. 33-94 (lire en ligne).
- Fatou 1920, p. 208-314.
Voir aussi
Articles connexes
Liens externes
- Jean-Christophe Yoccoz, « Ensembles de Julia de mesure positive et disques de Siegel des polynômes quadratiques », Séminaire Bourbaki, t. 48, 2005-2006, p. 385-402 (lire en ligne)
- Quelques ensemble de Julia sur YouTube
- Une application html pour générer des ensembles de Julia et voir le lien entre l'ensemble de Mandelbrot et les ensembles de Julia.
