Ensemble de Mandelbrot
En mathématiques, l'ensemble de Mandelbrot est une fractale définie comme l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes définie par récurrence par :
est bornée.


L'ensemble de Mandelbrot a été découvert par Gaston Julia et Pierre Fatou[1] avant la Première Guerre mondiale. Sa définition et son nom actuel sont dus à Adrien Douady, en hommage aux représentations qu'en a réalisées Benoît Mandelbrot dans les années 1980. Cet ensemble permet d'indicer les ensembles de Julia associés à la suite : à chaque point du plan complexe correspond un ensemble de Julia différent. Les points de l'ensemble de Mandelbrot correspondent précisément aux ensembles de Julia connexes, et ceux en dehors correspondent aux ensembles de Julia non connexes. Cet ensemble est donc intimement lié aux ensembles de Julia, ils produisent d'ailleurs des formes similairement complexes.
Les images de l'ensemble de Mandelbrot sont réalisées en parcourant les nombres complexes sur une région carrée du plan complexe et en déterminant pour chacun d'eux si le résultat tend vers l'infini ou pas lorsqu'on y itère une opération mathématique. On considère la partie réelle et imaginaire de chaque nombre complexe comme des coordonnées et chaque pixel est coloré selon la rapidité de divergence, ou si elle ne diverge pas.
Les images de l'ensemble de Mandelbrot exposent une limite élaborée qui révèle progressivement des détails récursifs toujours plus fins en augmentant le grossissement. La limite de l'ensemble est constituée de plus petites versions de la forme principale, donc la propriété fractale de l'autosimilarité s'applique à l'ensemble tout entier (et pas simplement à certaines parties).
L'ensemble de Mandelbrot est devenu populaire hors des mathématiques, comme inspiration artistique et comme exemple de structure complexe venant de l'application de règles simples. C'est l'un des exemples les plus connus de visualisation mathématique.
Historique

L'ensemble de Mandelbrot tire ses origines de la dynamique complexe, un domaine défriché par les mathématiciens français Pierre Fatou et Gaston Julia au début du XXe siècle...
La première représentation de cet ensemble apparaît en 1978 dans un article de Robert W. Brooks et Peter Matelski[2].
Le 1er mars 1980, au centre Thomas J. Watson de recherche IBM (dans l'État de New York), Benoît Mandelbrot obtient pour la première fois, une visualisation par ordinateur de cet ensemble[3]. Mandelbrot étudie l'espace des paramètres des polynômes quadratiques complexes dans un article publié en 1980[4].
En 1984, l'étude de l'ensemble de Mandelbrot commence réellement avec les travaux d'Adrien Douady et de John H. Hubbard[5], qui établissent ses propriétés fondamentales et baptisent l'ensemble en l'honneur de Mandelbrot.
En 1985, les mathématiciens Heinz-Otto Peitgen (en) et Peter Richter popularisent l'ensemble de Mandelbrot par des images de qualité qui frappent les esprits[6] - [7] - [8].
Dans le numéro d'août 1985 du magazine Scientific American, l'ensemble de Mandelbrot est présenté au grand public comme « l'objet mathématique le plus complexe jamais découvert » et présente l'algorithme qui permet de le tracer soi-même. La couverture de ce numéro reprend une image créée par Peitgen[9] - [10].
Les travaux de Douady et Hubbard coïncidaient avec un intérêt considérable pour la dynamique complexe et l'étude de l'ensemble de Mandelbrot a été le centre d'attention de ce domaine depuis. Parmi les mathématiciens qui apportèrent une contribution significative à l'étude de cet ensemble, il faut citer Tan Lei, Mikhail Lyubich, Curtis T. McMullen, John Milnor, Mitsuhiro Shishikura (en) et Jean-Christophe Yoccoz.
Propriétés
Définition
La théorie générale, développée par Pierre Fatou et Gaston Julia au début du XXe siècle, associe à toute fonction (suffisamment régulière) f(z, c) (à arguments et valeurs complexes) les ensembles de Julia Jc, définis (pour un c fixé) comme la frontière de l'ensemble des a complexes tels que la suite définie par z0 = a et zn+1 = f(zn, c) reste bornée (en module) ; pour la fonction particulière f(z, c) = z2 + c, on définit l'ensemble de Mandelbrot M comme l'ensemble des c pour lequel Jc est connexe. Fatou et Julia ont démontré[11] que cette définition est équivalente à celle donnée dans l'introduction, c'est-à-dire que c appartient à M si et seulement si la suite (zn) définie par z0 = 0 et zn+1 = zn2 + c reste bornée (en module) ; restant dans les réels, il s'agit donc des points de coordonnées (a,b) tels que les deux suites (xn) et (yn) définies par la récurrence x0 = y0 = 0 et xn+1 = xn2 – yn2 + a ; yn+1 = 2xnyn + b restent bornées.
Barrière du module égal à 2
Si la suite des modules des zn est strictement supérieure à 2 pour un certain indice alors, cette suite est croissante à partir de cet indice, et elle tend vers l'infini.
Pour que la suite (zn) soit bornée, il suffit donc qu'elle ne tende pas vers l'infini, et il faut qu'elle reste bornée par 2 (en module). Ceci fournit deux définitions de l'ensemble de Mandelbrot équivalentes à celle donnée en introduction, et prouve de plus que cet ensemble est inclus dans le disque fermé de centre 0 et de rayon 2.
Géométrie élémentaire
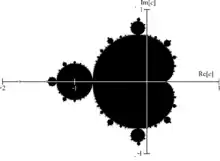
L'ensemble M de Mandelbrot est compact, symétrique par rapport à l'axe réel et contient le disque fermé de centre 0 et de rayon 1/4.
Son intersection avec l'axe réel est le segment [–2, 1/4].
Son aire est estimée autour de 1,50659177 ± 0,00000008[12].
Son centre de gravité est estimé à la position réelle –0,286 768 3 ± 0,000 000 1[12].
La principale structure remarquable est la cardioïde centrale, de centre et d'équation polaire . On peut aussi citer le disque de centre et de rayon .
Connexité
Douady et Hubbard ont montré, en 1985[13], que l'ensemble est connexe. Ce résultat n'était pas évident à l'observation des premiers tracés de Mandelbrot, qui faisait apparaître des « îlots » semblant détachés du reste. Pour ce faire, ils ont montré que le complémentaire de l'ensemble de Mandelbrot est conformément isomorphe au complémentaire dans ℂ du disque unité.
On conjecture que l'ensemble de Mandelbrot est localement connexe[14] - [15] - [16].
Autosimilarité



L'ensemble de Mandelbrot est autosimilaire dans le voisinage des points de Misiurewicz. Ces points sont denses sur toute la frontière de l'ensemble. On conjecture qu'il est également autosimilaire, à la limite, autour des points de Feigenbaum (ex. : −1,401 155 ou −0,152 8 + 1,039 7 i)[17].
Des versions réduites de l'ensemble de Mandelbrot apparaissent sur toute sa frontière, jusqu'à des grossissements infinis, avec de légères différences[18].
L'ensemble de Mandelbrot n'est pas, en général, strictement autosimilaire.
Universalité
L'ensemble de Mandelbrot M a un caractère universel pour de nombreuses fonctions holomorphes[18]. Des copies de M sont visibles sur les frontières de leurs bassins d'attraction, c'est-à-dire des ensembles des c pour lesquels les itérés f(f(…f(z)))) convergent vers un complexe donné. En voici quelques exemples, avec des fonctions transcendantes :
- (fonction cosinus)
- (fonction de Gauss)
On retrouve également M lors de l'itération d'une famille de fonctions cubiques telles que , par la méthode de Newton. L'ensemble des points ne convergeant pas vers une racine de ce polynôme prend la forme de M.
Là encore, l'autosimilarité n'est pas stricte.
 L'ensemble des points ne convergeant pas, pour une fonction cubique, par la méthode de Newton.
L'ensemble des points ne convergeant pas, pour une fonction cubique, par la méthode de Newton.![Points de non-convergence pour les itérées de f(z,c)=cos(z)+1/c, région [-0.09:-0.07]x[0.345:0.36].](https://img.franco.wiki/i/Mandelbrot_cosine_zoom.png.webp) Points de non-convergence pour les itérées de f(z,c)=cos(z)+1/c, région [-0.09:-0.07]x[0.345:0.36].
Points de non-convergence pour les itérées de f(z,c)=cos(z)+1/c, région [-0.09:-0.07]x[0.345:0.36].
Dimension de Hausdorff
La dimension de Hausdorff de la frontière de l'ensemble de Mandelbrot vaut 2. Ce résultat a été démontré en 1990 par Mitsuhiro Shishikura[19]. On ne sait pas si cette frontière a une mesure de Lebesgue (surface) positive.
Lien avec l'équation logistique

Les paramètres de M, dans l'intervalle réel [–2, 1/4], peuvent être mis en correspondance bijective avec ceux de l'équation logistique : la correspondance étant donnée par :
Lien avec les ensembles de Julia
L'ensemble de Mandelbrot M peut être défini comme l'ensemble des complexes c pour lesquels l'ensemble de Julia correspondant, Jc, est connexe. Mais, plus précisément, on a (à la limite) identité entre Jc et M au voisinage de c, lorsque c appartient à la frontière de M[20]. Ainsi, il y a une correspondance proche entre la géométrie de l'ensemble de Mandelbrot à un point donné et la structure de l'ensemble de Julia lui correspondant. Par exemple, un point est dans l'ensemble de Mandelbrot exactement là où l'ensemble de Julia correspondant est connexe.
Ce principe est exploité dans beaucoup de preuves et découvertes profondes sur l'ensemble de Mandelbrot. Par exemple, Mitsuhiro Shishikura a prouvé que la frontière de l'ensemble de Mandelbrot possède une dimension de Hausdorff de 2 et que l'ensemble de Julia correspondant à un point de cette frontière a aussi une dimension 2[21].
Jean-Christophe Yoccoz a prouvé que l'ensemble de Julia est un espace localement connexe pour certains paramètres, avant de l'établir également pour l'ensemble de Mandelbrot aux points correspondant à ces paramètres[22].
Bourgeons, antennes et périodicités
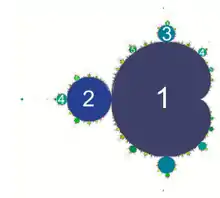
L'ensemble de Mandelbrot fait apparaître nombre de structures en forme de bourgeons entourant une structure principale en forme de cardioïde.
- La cardioïde est l'ensemble des points c qui convergent vers un point fixe (période 1). Ce sont les points de la forme pour tout appartenant au disque unité.
- Le bourgeon principal, à gauche de la cardioïde, lui est attaché au point c = –3/4. Il s'agit d'un disque centré en c = –1 et de rayon 1/4. Il s'agit de l'ensemble des points paramètres qui, à la limite, convergent vers un cycle de période 2.
- Les autres bourgeons tangents à la cardioïde sont les points admettant d'autres périodicités. Pour tout nombre rationnel p/q, avec p et q premiers entre eux, il existe un bourgeon presque circulaire tangent à la cardioïde au point . Chacun de ces bourgeons est appelé « bourgeon p/q ». Il s'agit de l'ensemble des points paramètres convergeant vers un cycle de période q.
- Enfin, chaque bourgeon porte lui-même des bourgeons, représentatifs d'une périodicité différente, selon le même schéma. Par exemple, le bourgeon à gauche du grand bourgeon de période 2 a une périodicité de période 4. Le bourgeon immédiatement à sa gauche est de période 8, puis 16, etc., suivant ainsi le motif de doublement de période du diagramme de bifurcation de l'équation logistique.

Les bourgeons sont également surmontés de filaments en forme d'antenne. Le nombre d'antennes est directement lié à la périodicité du bourgeon. Ainsi, compter le nombre d'antennes permet de déterminer la périodicité du bourgeon.
Dessiner l'ensemble
On a vu plus haut que dès que le module d'un zn est strictement plus grand que 2, la suite diverge vers l'infini, et donc c est en dehors de l'ensemble de Mandelbrot. Cela nous permet d'arrêter le calcul pour les points ayant un module strictement supérieur à 2 et qui sont donc en dehors de l'ensemble de Mandelbrot. Pour les points de l'ensemble de Mandelbrot, le calcul n'arrivera jamais à terme, donc il doit être arrêté après un certain nombre d'itérations déterminé par le programme. Il en résulte que l'image affichée n'est qu'une approximation du vrai ensemble.
Bien que cela n'ait aucune importance sur le plan mathématique, la plupart des programmes générant des fractales affichent les points en dehors de l'ensemble de Mandelbrot dans différentes couleurs. La couleur attribuée à un point n'appartenant pas à l'ensemble dépend du nombre d'itérations au bout desquelles la suite correspondante est déclarée divergente vers l'infini (par exemple quand le module est strictement supérieur à 2). Cela donne plusieurs zones concentriques, qui entourent l'ensemble de Mandelbrot. Les plus éloignées sont constituées des points c pour lesquels la suite (zn) tend « plus rapidement » vers l'infini. Ces différentes zones délimitent d'une manière plus ou moins précise l'ensemble de Mandelbrot.
Le nombre maximum d'itérations influe donc fortement sur la représentation de l'ensemble de Mandelbrot. En effet si la forme de base de l'ensemble ne varie pas outre mesure à partir de 100 itérations il n'en est pas de même pour tous les centres et tous les zooms de cet ensemble.
Cardioïde / bourgeon principal
Un moyen de limiter les calculs est de trouver au préalable les points appartenant à la cardioïde et au bourgeon principal, c'est-à-dire au disque de centre (–1, 0) et de rayon 1/4. Ces points coûtent particulièrement cher en calculs, puisqu'ils appartiennent à l'ensemble de Mandelbrot, et nécessitent donc d'aller jusqu'au maximum d'itérations. Avant de passer un point de coordonnées dans l’algorithme itératif, il faut donc vérifier :
- si avec alors le point appartient à la cardioïde, donc à l'ensemble de Mandelbrot ;
- si alors le point appartient au disque de centre (–1, 0) et de rayon 1/4, c'est-à-dire au bourgeon principal, et donc à l'ensemble de Mandelbrot.
Les autres bourgeons n'ont pas de test équivalent, puisqu'ils ne sont pas parfaitement circulaires. Il est néanmoins possible de vérifier si un point appartient à un cercle que l'on sait inscrit dans un de ces bourgeons, permettant à la plupart des points de ces derniers de ne pas lancer l'algorithme itératif.
Algorithme par perturbation
Il est possible de reformuler l'équation principale, de manière à raisonner sur la différence d'évolution par rapport à un point voisin. Cette méthode permet de ramener ces différences à une faible précision (vingtaine de chiffres significatifs), dans le domaine des unités de calcul en virgule flottante matérielles de l'ordinateur, qui sont beaucoup plus rapides que les bibliothèques d'arithmétique multiprécision qui ne sont pas autant accélérées matériellement. L'ensemble est ainsi calculé à partir d'un (ou plusieurs) points de référence, calculés de manière absolue.
Si on raisonne en absolu, les nombres mis en œuvre pour le calcul de l'ensemble peuvent atteindre des milliers de chiffres significatifs pour des grands niveaux de zoom, et s'accroissant davantage avec le zoom. Avec cet algorithme, la vitesse de calcul reste relativement constante selon le niveau de zoom, la vitesse de calcul dépendant plus de la complexité de la scène[23].
Cet algorithme est à la base d'un des programmes de calcul le plus rapide de l'ensemble de Mandelbrot en 2017 : Kalles Fraktaler[24].
Principe[23] :
Tous les , calculés à partir des de référence mémorisés, ont une faible précision, permettant d'utiliser les unités de calcul en virgule flottante matérielles de l'ordinateur pour les opérations les plus nombreuses et coûteuses.
Le calcul peut encore être davantage optimisé en exprimant en utilisant l'approximation[23] :
avec ne dépendant pas de , mais seulement de (série du point de référence à partir duquel on calcule les perturbations).
Donc, une fois calculés et mémorisés tous les pour le point de référence (), on peut rechercher directement pour tout point voisin (en faisant varier ), par recherche dichotomique, le qui provoque la divergence de la suite (puisqu'on n'a pas besoin du pour calculer ) et le calcul d'un point se fait avec une complexité en temps au lieu de , étant le nombre maximum d'itérations[25].
Un zoom commenté

L'ensemble de Mandelbrot doit beaucoup sa popularité à la variété et la beauté de ses structures et à la profondeur infinie de ses détails, mais aussi à la possibilité de l'explorer soi-même à l'aide des nombreux logiciels aujourd'hui disponibles.
La séquence d'exploration commentée ci-dessous est un zoom profond vers la valeur de c = –0,743643887037151 + 0,13182590420533i, à travers nombre de motifs caractéristiques. Le rapport de grossissement entre la dernière et la première image est d'environ 60 milliards (si la dernière image était en taille réelle, la première ferait une petite dizaine de fois la distance Terre-Lune). La séquence entière (et sa suite jusqu'à un grossissement d'environ 1030) peut être visionnée sur l'animation ci-contre.
| Étape | Description |
|---|---|
 | L'ensemble de Mandelbrot initial.
Nous allons zoomer sur la vallée située entre la cardioïde et le bourgeon principal. |
 | Cette vallée a été baptisée « vallée des hippocampes ». |
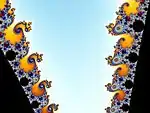 | À gauche, des spirales doubles, à droite les « hippocampes ».
Nous zoomons sur l'un d'eux. |
 | Un « hippocampe », tête en bas. Cet hippocampe est composé de 25 « antennes » consistant en 2 groupes de 12 et un filament relié à la cardioïde. Nous en déduisons que le bourgeon qui le porte a une périodicité de 25. Le point de rencontre de ces antennes est un « point de Misiurewicz ». Sur la plus longue antenne, celle qui mène à la « queue » de l'hippocampe, on reconnaît une copie réduite de l'ensemble de Mandelbrot, appelée aussi « satellite ».
Nous zoomons maintenant sur la queue de l'hippocampe. |
 | L'extrémité de la queue, enroulée en spirale, est aussi un point de Misiurewicz.
Nous zoomons sur le haut de l'image. |
 | Une section de la queue. Cette structure complexe est composée d'un seul et unique chemin qui mène jusqu'à l'extrémité de la queue. L'ensemble de Mandelbrot est un ensemble simplement connexe, ce qui signifie qu'il n'y a ni boucles, ni ilots.
Zoomons vers le centre de l'image. |
 | Un deuxième « satellite » (ou « minibrot ») apparait, au cœur de ce carrefour. Un exemple d'autosimilarité : La frontière de l'ensemble de Mandelbrot contient une infinité de copies de lui-même. Quel que soit le lieu on l'on zoome on en trouvera toujours au moins un. Les deux spirales sont le début d'une série de couronnes concentriques, avec le satellite en son centre.
Nous zoomons vers ce satellite. |
 | Chacune de ces couronnes est composée de spirales similaires. Leur nombre s'accroit en puissances de 2, un phénomène typique de l'environnement des satellites. Le chemin vers l'extrémité de la queue entre dans le satellite par le point d'inflexion de la cardioïde et ressort par l'extrémité son antenne. |
 | L'antenne du satellite. On peut distinguer plusieurs satellites du deuxième ordre.
Zoomons en haut à droite de l'image. |
 | La « vallée des hippocampes » du satellite. Toutes les structures déjà rencontrées précédemment réapparaissent. |
 | Spirales doubles et hippocampes. Contrairement à la première vallée, celle-ci est peuplée, en plus, de légères structures spirales. Dans un satellite d'ordre n cohabitent n+1 types de structures différentes. Pour ce satellite d'ordre 1 coexistent donc deux types de structures différentes.
Nous zoomons sur une double spirale, à gauche de la vallée. |
 | Double-spirale avec satellites du deuxième ordre.
Nous zoomons, maintenant, sur une des structures dentelées blanches en haut à droite de l'image. |
 | Ces structures légères rappellent celles de certains ensembles de Julia. Là encore, ce motif très torturé n'est constitué que d'un seul filament.
Nous zoomons sur le « double-crochet » que l'on distingue à droite de l'image. |
 | Ce double crochet rappelle, encore une fois, la forme en spirale de la queue d'un hippocampe.
Nous zoomons vers le motif central. |
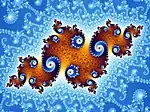 | Des îlots apparaissent, à la manière d'une poussière de Cantor. La forme générale est celle d'un ensemble de Julia Jc. Toutefois, contrairement à un ensemble de Julia, ces points sont tous connectés, car nous sommes toujours dans l'ensemble de Mandelbrot. La forme générale de cet ensemble n'est pas celle de l'ensemble de Julia associé à cette position. Il s'agit de l'ensemble de Julia que nous aurions obtenu si nous avions sélectionné, au début de notre exploration, un point à proximité d'une double spirale au lieu d'un hippocampe.
Ces structures sont elles-mêmes connectées à une structure centrale que nous pourrions découvrir si nous poussions encore plus loin le grossissement. En théorie, le grossissement pourrait ainsi être infini, et faire découvrir sans cesse de nouvelles structures. Pour en voir davantage, cliquer sur l'animation en haut à droite de cette section. |
Généralisations et variantes


L'ensemble de Mandelbrot peut être généralisé pour des puissances d réelles supérieures à 2 pour z ↦ zd + c. Ces généralisations sont parfois appelées « multibrot », mais pour certains auteurs (comme McMullen), le terme « ensemble de Mandelbrot » doit également désigner ces généralisations.
 Puissance 3
Puissance 3 Puissance 4
Puissance 4 Puissance 5
Puissance 5 Puissance 6
Puissance 6
Une modification de la méthode de traçage, proposée par Melinda Green en 1993, mène à une variante baptisée « Buddhabrot »[26]. On y voit la densité des points visités par les orbites correspondant aux valeurs de c qui divergent, donc choisies à l'extérieur de l'ensemble de Mandelbrot.

En 3 dimensions, il n'existe pas de structure de corps comparable à celle des nombres complexes, donc pas d'extension « naturelle ». Notons toutefois l'extension de Daniel White, réalisée en 2009, baptisée « Mandelbulb[27]. »
En 4 dimensions, l'extension naturelle au corps des quaternions a été étudiée par John Holbrook en 1987[28]. D'autres résultats théoriques ont été traités pour l'ensemble de Mandelbrot quaternionique [29] - [30] (voir vidéo) défini avec un polynôme quadratique de la forme .

En 2000, Dominic Rochon a utilisé l’anneau commutatif des nombres bicomplexes pour donner une nouvelle version de l’ensemble de Mandelbrot en dimension trois et quatre. De ses travaux émerge le « Tétrabrot »[31] - [32].
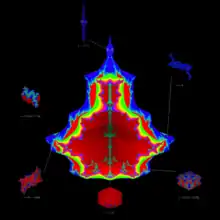
Il est aussi possible de généraliser encore, et de considérer plutôt des itérations quelconques .
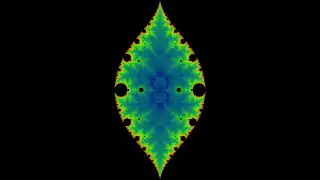 Une variante pour f(z,c)=cos(z/c)
Une variante pour f(z,c)=cos(z/c) f(z,c)=sinh(z)+1/c²
f(z,c)=sinh(z)+1/c²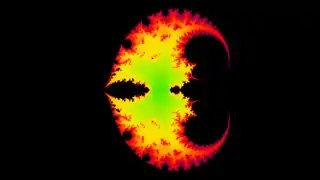 f(z,c)=cos(z)+1/c
f(z,c)=cos(z)+1/c f(z,c)=cz-1e-c (intégrande de la fonction Gamma)
f(z,c)=cz-1e-c (intégrande de la fonction Gamma) f(z,c)=sinh(z)+1/ck (k variant entre 0.1 et 10)
f(z,c)=sinh(z)+1/ck (k variant entre 0.1 et 10) f(z,c)=z²+sin(c3)
f(z,c)=z²+sin(c3) f(z,c)=z²+c3-δ, avec δ≈-1.401155 le point de Feigenbaum
f(z,c)=z²+c3-δ, avec δ≈-1.401155 le point de Feigenbaum f(z,c)=z²+(c3+0.7-0.2i)3+i (zoom en 0.36+0.7i)
f(z,c)=z²+(c3+0.7-0.2i)3+i (zoom en 0.36+0.7i)
Références culturelles
L'ensemble de Mandelbrot est l'un des objets mathématiques les plus populaires et les plus connus. Il est évoqué par divers artistes, dans des livres ou des musiques notamment :
- La musique de Jonathan Coulton Mandelbrot Set est un hommage à l'ensemble de Mandelbrot lui-même et à son « père », Benoît Mandelbrot. Les paroles rappellent entre autres la définition par récurrence de l'ensemble[33] - [34] - [35].
- Le second livre de la série Mode (livres) (en) de Piers Anthony, "Fractal Mode", décrit un monde qui est un modèle 3D parfait de l'ensemble[36].
- Le roman de Arthur C. Clarke "Le Fantôme venu des profondeurs" contient un lac artificiel créé pour répliquer la forme de l'ensemble de Mandelbrot[37].
- Le chanteur de heavy metal sud-coréen Norazo (en)a fait un clip musical Ni pal za ya (ton destin), qui commence avec une vidéo hypnotique de l'ensemble de Mandelbrot[38].
- L'album Jupiter's Darling du groupe de rock américain Heart présente un ensemble de Mandelbrot sur sa couverture. L'ensemble est tourné de manière que le cardioïde soit en haut et que la figure ressemble à un cœur.
Logiciels générateurs de fractales
- ChaosPro - (propriétaire - pour Windows)
- FractaNep (gratuit - pour Windows)
- Fractile Plus (gratuit pour iOS)
- Fractint (propriétaire - porté sur de nombreuses plates-formes)
- Gecif
- Gnofract 4D - (puissant et rapide - pour Linux, FreeBSD ou Mac OS X)
- Kalles Fraktaler (gratuit - pour Windows)
- Mandelbulb 3D (gratuit pour de nombreuses plateformes, exemple de réalisation : Vidéo)
- XaoS (Logiciel libre - Licence GPL, pour Windows, Mac OS X, Linux et systèmes type Unix)
Notes et références
- Voir à ce sujet : Jean-Pierre Louvet les fractales sur le site de futura-science ; en réalité, la première description précise de l'ensemble semble due à Brooks et Matelski (voir la section historique).
- (en) Robert Brooks et Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), in « Riemann Surfaces and Related Topics », ed. Kra and Maskit, Ann. Math. Stud. 97, 65–71 (ISBN 0-691-08264-2).
- (en) R. P. Taylor et J. C. Sprott, « Biophilic Fractals and the Visual Journey of Organic Screen-savers », Nonlinear Dynamics, Psychology, and Life Sciences, Society for Chaos Theory in Psychology & Life Sciences, vol. 12, no 1, (lire en ligne).
- (en) Benoît Mandelbrot, « Fractal aspects of the iteration of for complex », Annals NY Acad. Sci., vol. 357, , p. 249/259.
- Adrien Douady et John H. Hubbard, Étude dynamique des polynômes complexes, Prépublications mathématiques d'Orsay 2/4 (1984 / 1985).
- (en) Heinz-Otto Peitgen, The Beauty of Fractals, Heidelberg, Springer-Verlag, (ISBN 0-387-15851-0).
- (en) Frontiers of Chaos, Exhibition of the Goethe-Institut by H. O. Peitgen, P. Richter, H. Jürgens, M. Prüfer, D.Saupe.
- (en) James Gleick, Chaos : Making a New Science, Londres, Cardinal, , p. 229.
- (en) A. K. Dewdney (en), « Computer recreations : A computer microscope zooms in for a close look at the most complicated object in mathematics », Scientific American, , p. 16-24 (lire en ligne).
- Fractals: The Patterns of Chaos. John Briggs. 1992. p. 80.
- Cf. (en) A. Douady et J. Hubbard, « On the dynamics of polynomial-like mappings », ASENS, vol. 18, , p. 287-343 (lire en ligne) et (en) Paul Blanchard, « Complex analytic dynamics on the Riemann sphere », Bull. Amer. Math. Soc. (N. S.), vol. 11, no 1, , p. 1-246 (lire en ligne).
- Mrob.com.
- Douady et Hubbard 1985.
- http://smf4.emath.fr/en/InfoDiverses/Carnet/Douady/DepecheAFP.html
- http://www.math.cornell.edu/~hubbard/OrsayFrench.pdf
- « C.V. de Jean-Christophe Yoccoz », sur Académie des sciences.
- (en) J. Milnor, « Self-Similarity and Hairiness in the Mandelbrot Set », dans Computers in Geometry and Topology, M. Tangora (éditeur), Dekker, New York, p. 211-257.
- (en) Curtis T. McMullen, « The Mandelbrot set is universal », 1998, abstract.
- (en) Mitsuhiro Shishikura, « The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets », Ann. of Math., vol. 147, 1998, p. 225-267 (publication originale de 1991 Stony Brook IMS Preprint, arXiv:math.DS/9201282).
- (en) Tan Lei, « Lei.pdf Similarity between the Mandelbrot set and Julia Sets », Comm. Math. Phys., vol. 134, 1990, p. 587-617.
- (en) Mitsuhiro Shishikura, The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets, « math.DS/9201282 », texte en accès libre, sur arXiv.
- (en) J. H. Hubbard, Local connectivity of Julia sets and bifurcation loci: three theorems of J.-C. Yoccoz.
- « Superfractalthings Maths ».
- « Kalles Fraktaler 2 ».
- (en) Buddhabrot fractal method.
- Variantes en 3D.
- (en) J. A. R. Holbrook, « Quaternionic Fatou-Julia sets », Ann. Sc. Math. Quebec, vol. 1, 1987, p. 79-94.
- S. Bedding and K. Briggs, "Iteration of Quaternion Maps", Int. J. Bifur. Chaos Appl. Sci. Eng., 5:877–881, 1995. DOI 10.1142/S0218127495000661
- J. Gomatam, J. Doyle, B. Steves and I. McFarlane, "Generalization of the Mandelbrot Set: Quaternionic Quadratic Maps", Chaos, Solitons & Fractals, 5:971–985, 1995. DOI 10.1142/S0218127495000661
- Dominic Rochon, « A Generalized Mandelbrot Set For Bicomplex Numbers », Fractals, vol. 8, no 4, , p. 355–368 (DOI 10.1142/S0218348X0000041X)
- É. Martineau and D. Rochon, "On a Bicomplex Distance Estimation for the Tetrabrot", International Journal of Bifurcation and Chaos, 15(6):501–521, 2005. DOI 10.1142/S0218127405013873
- (en) « Never Trend Away: Jonathan Coulton on Benoit Mandelbrot », sur www.wired.com.
- (en) « Mandelbrot Set/Lyrics - JoCopedia, the Jonathan Coulton wiki », sur www.jonathancoulton.com.
- (en) Arthur Archibald Wonderfluff XIII, « Jonathan Coulton - Mandelbrot Set », sur www.youtube.com, .
- (en) Piers Anthony, Fractal Mode, HarperCollins, , 302 p. (ISBN 978-0-246-13902-3, lire en ligne).
- (en) Arthur C. Clarke, The Ghost From The Grand Banks, Orion, , 274 p. (ISBN 978-0-575-12179-9, lire en ligne).
- Vidéo : https://www.youtube.com/watch?v=s0UjELAUMjE.









![z\mapsto \lambda z(1-z),\quad \lambda\in[1,4],](https://img.franco.wiki/i/5086f195140d8764b510e9a5c076904e403f3631.svg)

























