Espace localement connexe

En topologie, on dit qu’un espace est connexe lorsqu’il est fait « d’une seule pièce ». La question naturelle qui suit est de savoir si tout espace topologique peut être décrit comme la réunion disjointe (dans la catégorie des espaces topologiques) de ses composantes connexes ; en d’autres termes, peut-on considérer que lorsqu’on connait toutes les « pièces » d’un espace topologique, on sait tout de cet espace ? Une condition nécessaire et suffisante pour cela est que toutes les composantes connexes soient ouvertes.

La réponse est donc en général négative. Par exemple, l’ensemble ℚ des nombres rationnels muni de sa topologie usuelle a pour composantes connexes les singletons — on dit alors que ℚ est totalement discontinu. Or une union disjointe (dans la catégorie des espaces topologiques) de singletons est un espace discret donc non homéomorphe à ℚ.

On dit alors qu’un espace topologique est localement connexe lorsqu’il est homéomorphe à l’union disjointe de ses composantes connexes et que cela est vrai aussi de chaque ouvert de cet espace.

Distinguer les espaces grâce à leurs composantes connexes est le stade zéro de la classification des espaces topologiques. De ce point de vue, l’utilisation des espaces localement connexes est motivée par la remarque suivante. Le foncteur π₀ qui à tout espace topologique associe l’ensemble de ses composantes connexes n’a pas les bonnes propriétés — il ne commute pas à toutes les limites inductives. Il les acquiert si on le restreint à la catégorie des espaces localement connexes.

Un espace topologique est dit localement connexe lorsque chacun de ses points admet une base de voisinages connexes.

• Un espace X est localement connexe si et seulement si, pour tout ouvert U de X, les composantes connexes de U sont ouvertes[1] (autrement dit : si les ouverts connexes forment une base de la topologie). En particulier, dans un espace localement connexe :
  • tout ouvert est localement connexe ;
  • les parties à la fois ouvertes et fermées sont exactement les unions de composantes connexes.
• La connexité locale est préservée par homéomorphisme. Ainsi, les variétés sont localement connexes car les espaces affines réels le sont.
• Tout produit fini, tout quotient d'espaces localement connexes est encore localement connexe.
• Un produit infini d'espaces localement connexes n'est pas toujours localement connexe (penser à {0, 1}^ℕ) mais il l'est si tous les facteurs sont, de plus, connexes[2].

Le « peigne » (en) est connexe, mais pas localement connexe.

• Tout espace localement connexe par arcs est localement connexe (puisque tout espace connexe par arcs est connexe). Les exemples les plus classiques sont ℝ, ℂ, ℝⁿ, etc.
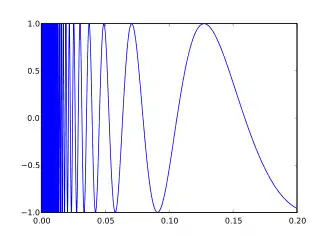
• Dans ℝ² muni de sa topologie usuelle, un exemple d'espace connexe qui n'est pas localement connexe est la « courbe sinus du topologue » (figure ci-dessus). Un exemple de même nature est la partie A = ({0}×ℝ)∪(ℝ×ℚ) : tout point de A possède dans A un voisinage connexe (à savoir A lui-même) mais ne possède pas forcément de base de voisinages connexes.
• Un autre exemple classique de partie connexe de ℝ² qui n'est pas localement connexe est le peigne (figure ci-contre).

La catégorie Locon des espaces localement connexes est une sous-catégorie pleine de la catégorie Top des espaces topologiques. Le foncteur d’inclusion i : Locon → Top est pleinement fidèle et admet un adjoint à droite L : Top → Locon. On dit alors que Locon est une sous-catégorie coréflexive de Top.

De ce fait, et comme Top est complète et cocomplète, la catégorie Locon est elle aussi complète et cocomplète.

Le foncteur L associe à tout espace topologique X, le même ensemble sous-jacent muni d’une nouvelle topologie, engendrée par les composantes connexes des ouverts de X.

Par exemple, L(ℚ) est l’ensemble des rationnels muni de la topologie discrète.

Grâce à la catégorie Locon, le foncteur π₀ admet à présent un adjoint à droite (et préserve donc toutes les limites inductives). C’est le foncteur Δ qui à tout ensemble X associe l’espace topologique ayant comme ensemble sous-jacent X et muni de la topologie discrète.