Courbe sinus du topologue

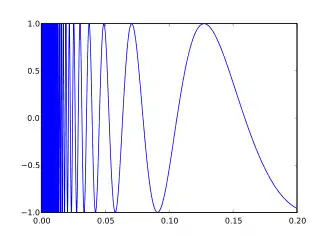
La courbe sinus du topologue T est définie comme la courbe représentative de la fonction f qui à tout x strictement positif associe sin(¹⁄_x) et qui vaut 0 en 0 :

${\displaystyle T=\left\{\left.\left(x,\sin {\frac {1}{x}}\right)\right|x\in ]0,1]\right\}\cup \{(0,0)\}.}$

Cette courbe est munie de la topologie induite par celle du plan euclidien.

L'ensemble des valeurs d'adhérence de la fonction f en 0 est égal à celui de la fonction sin en +∞, c'est-à-dire au segment [-1, 1] (en particulier, f n'a pas de limite en 0). Ce phénomène est illustré par l'accumulation d'oscillations de la courbe au voisinage de l'origine.

La courbe sinus du topologue T est connexe mais ni localement connexe ni connexe par arcs. C'est parce que l'ensemble contient le point (0,0) mais qu'il n'est pas possible de relier la fonction à l'origine ni de tracer un chemin.

L'espace T est l'image continue d'un espace localement compact (T est l'image de {−1} ∪ ]0, 1] par l'application g définie par g(−1) = (0,0) et g(x) = (x, sin(1/x)) pour x > 0), mais n'est pas localement compact lui-même.

La dimension topologique de T est 1.

Le « cercle polonais ».

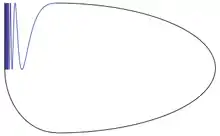
Deux variantes de la courbe sinus du topologue ont d'autres propriétés intéressantes.

La courbe sinus fermée du topologue peut être définie en prenant la courbe sinus du topologue et en ajoutant l'ensemble des points adhérents, ${\displaystyle \{(0,y)\mid y\in [-1,1]\}}$. Cet espace est fermé et borné et donc compact par le théorème de Borel-Lebesgue, mais a des propriétés similaires à la courbe sinus du topologue — il est connexe mais ni localement connexe ni connexe par arcs.

La courbe sinus prolongée du topologue peut être définie en prenant la clôture topologique de T et en ajoutant l'ensemble ${\displaystyle \{(x,1)\mid x\in [0,1]\}}$. Cet espace est connexe par arcs mais non localement connexe.

Le cercle polonais (de), obtenu en ajoutant à la courbe sinus fermée du topologue un arc joignant (0, –1) à (1, sin 1), n'est pas contractile, bien que tous ses groupes d'homotopie soient triviaux.

(en) Lynn Arthur Steen et J. Arthur Seebach, Jr., Counterexamples in Topology, Mineola, NY, Dover, 1995, 244 p. (ISBN 978-0-486-68735-3, lire en ligne), p. 137-138, lien Math Reviews