Ensemble de Multibrot
En mathématiques, l'ensemble de multibrot est l'ensemble des points c du plan complexe pour lesquels la suite de nombres complexes définie par récurrence par :
où d ≥ 2,
L'exposant d peut être généralisé à des valeurs négatives et fractionnelles[4].
Ce nom est la contraction de multiple et ensemble de Mandelbrot (ce dernier correspond au cas particulier où d=2).
Beaucoup de représentations graphiques sont disponibles, mais pour l'instant, aucune n'a réussi à afficher un empilement 3D de différentes images pour que l'évolution générale de la forme puisse être vue depuis un autre endroit que d'en haut.
Exemples[5]
Le cas de
est l'ensemble de Mandelbrot classique depuis lequel le nom est dérivé.
Les ensembles pour les autres valeurs de d présentent aussi des images fractales [6] lorsqu'ils sont tracés sur le plan complexe.
Chaque exemple des différentes puissances d ci-dessous est tracé à la même échelle. Les valeurs de c appartenant à l'ensemble sont noires. Les valeurs de c dont les valeurs ne sont pas bornées après itérations n'appartiennent pas à l'ensemble et sont représentées en différentes couleurs pour montrer leurs contours. Les couleurs dépendent du nombre d'itérations nécessaires pour que la valeur dépasse la magnitude définie.
Puissances positives
L'exemple d = 2 est l'ensemble de Mandelbrot original. Les exemples pour d > 2 sont souvent appelés ensembles de multibrot. Ces ensembles incluent l'origine et ont un périmètre fractal, avec (d − 1) axes de symétrie rationnel(s).
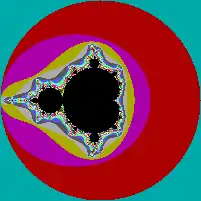 z z2 + c |
 z z3 + c |
 z z4 + c |
 z z5 + c |
 z z6 + c |
 z z96 + c |
 z z96 + c détail x40 |
Puissances négatives
Lorsque d est négatif, l'ensemble encercle l'origine mais ne l'inclut pas. Il y a un comportement complexe intéressant entre l'ensemble et l'origine, une zone en forme d'étoile avec (1 − d) axes de symétrie rationnel(s). L'ensemble semble avoir un périmètre circulaire, mais cette illusion est créée par le rayon maximal autorisé par l'algorithme et n'est pas la vraie limite de l'ensemble, qui s'étend en réalité dans toutes les directions jusqu'à l'infini.
 z z−2 + c |
 z z−3 + c |
 z z−4 + c |
 z z−5 + c |
 z z−6 + c |
Puissances fractionnelles
L'inclusion de puissances fractionnelles ne montre rien de particulier, si ce n'est l'apparition des axes de symétrie que l'on observe avec des puissances entières. La transition semble régulière, le nouvel axe "apparait" sans causer d'irrégularités par rapport aux formes précedemment obtenues.
Tracer l'ensemble
Toutes les images ci-dessus sont tracées avec l'algorithme d'Évasion du Temps qui identifie des points hors de l'ensemble de manière simple. On peut révéler beaucoup plus de détails fractals en traçant l'exposant de Liapounov[7] comme le montre l'exemple ci-dessous.
L'exposant de Liapounov est le taux de croissance de l'erreur d'une séquence donnée. On calcule d'abord la séquence d'itération avec N itérations, puis on calcule l'exposant avec
et si l'exposant est négatif, la séquence est stable. Les pixels blancs sur l'image sont les paramètres c pour lesquels l'exposant est positif, c'est-à-dire instable.
Les couleurs montrent la période des cycles auxquels les orbites sont attirées. Tous les points bleu foncé (extérieur) sont attirés par un point fixe et tous les points au milieu, en bleu plus clair, sont attirés par un cycle à deux périodes, et ainsi de suite.


Pseudocode
ALGORITHME D'ÉVASION DU TEMPS
=====================
Pour chaque pixel sur l'écran, faire :
{
x = x0 = x coordonnée du pixel
y = y0 = y coordonnée du pixel
itération = 0
max_itération = 1000
while ( x*x + y*y <= (2*2) AND itération < max_itération )
{
/* INSÉRER LE(S) CODE(S) POUR Z^d DEPUIS LE CODE CI-DESSOUS */
itération = itération + 1
}
if ( itération == max_itération )
then
colour = noir
else
colour = itération
plot(x0,y0,couleur)
}
La valeur complexe z a les coordonnées (x, y) sur le plan complexe et est élevée à des puissances différents dans la boucle d'itération par les codes montrés ci-dessus. Les puissances non présentes dans ce code sont obtenues en concaténant des codes montrés.
| z−1 | z2 (pour l'ensemble de Mandelbrot) | z3 | z5 | zn |
|---|---|---|---|---|
d=x^2+y^2 if d=0 then ESCAPE x = x/d + a y= -y/d + b |
xtmp=x^2-y^2 + a y=2*x*y + b x=xtmp |
xtmp=x^3-3*x*y^2 + a y=3*x^2*y-y^3 + b x=xtmp |
xtmp=x^5-10*x^3*y^2+5*x*y^4 + a y=5*x^4*y-10*x^2*y^3+y^5 + b x=xtmp |
xtmp=(x*x+y*y)^(n/2)*cos(n*atan2(y,x)) + a y=(x*x+y*y)^(n/2)*sin(n*atan2(y,x)) + b x=xtmp |
Notes et références
- (en) « Definition of multibrots » (consulté le )
- (en) « Multibrots » (consulté le )
- (en) « Homeomorphisms on Edges of the Mandelbrot Set, Wolf Jung, p. 23, The Multibrot set Md is the connectedness locus of the family of unicritical polynomials zd+c, d ≥ 2 »
- (en) « WolframAlpha Computation Knowledge Engine »
- (en) « http://www.nihilogic.dk/labs/javascript_canvas_fractals/ Javascript application "Multibrots, variations on the Mandelbrot theme created by raising z to higher powers, rather than the standard z2 of the Mandelbrot. »
- (en) « Animated morph of multibrots d = −7 to 7 » (consulté le )
- (en) Ken Shirriff, « An Investigation of Fractals Generated by z → 1/zn + c », Computers & Graphics, vol. 17, no 5, , p. 603–607 (DOI 10.1016/0097-8493(93)90012-x, lire en ligne, consulté le )
- P.-O. Parisé & D. Rochon. A study of dynamics of the tricomplex polynomial ηp+c, Non Lin. Din., (2015), https://link.springer.com/article/10.1007/s11071-015-2146-6



