Théorème de Stone-Weierstrass
En mathématiques, le théorème de Stone-Weierstrass est une généralisation du théorème d'approximation de Weierstrass[1] en analyse réelle, selon lequel toute fonction continue définie sur un segment peut être approchée uniformément par des fonctions polynomiales.
La généralisation par Marshall Stone étend ce résultat aux fonctions continues définies sur un espace compact[2] et à valeurs réelles, en remplaçant l'algèbre des fonctions polynomiales par une sous-algèbre ou un treillis vérifiant des hypothèses naturelles.
Théorème d'approximation de Weierstrass
Soit f une fonction continue de [a, b] dans ℝ.
Pour tout ε > 0, il existe une fonction polynomiale p à coefficients réels telle que pour tout x dans [a, b], |f(x) – p(x)| ≤ ε.
ou encore :
Il existe une suite (Pn) de polynômes convergeant uniformément vers f sur [a, b].
L'ensemble C([a, b]) des fonctions à valeurs réelles et continues sur [a, b], muni de la norme infinie , est une algèbre de Banach (c.-à-d. une ℝ-algèbre associative et un espace de Banach telle que pour tout f et g). L'ensemble des fonctions polynomiales forme une sous-algèbre de C([a, b]) et le théorème d'approximation de Weierstrass affirme que cette sous-algèbre est dense dans C([a, b]).
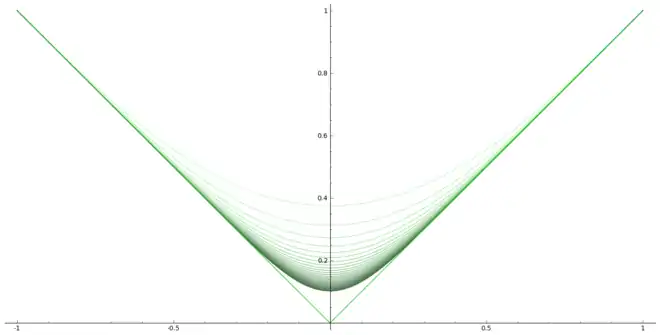
Ci-dessous, un exemple d'une suite de polynômes convergeant vers la fonction valeur absolue sur l'intervalle [–1, 1].
Autres versions et généralisations
Version trigonométrique
Pour toute fonction f continue périodique, il existe une suite de polynômes trigonométriques qui converge uniformément vers f.
Issu de la théorie des séries de Fourier, le théorème de Fejér donne un exemple constructif d'une telle suite.
Loi des grands nombres
S. Bernstein a donné une démonstration constructive et probabiliste du théorème de Weierstrass sur [0, 1], en prouvant qu'on pouvait prendre :
où les sont les polynômes de Bernstein.
En effet, si X est une variable aléatoire suivant la loi binomiale de paramètres (n, x), alors Pn(x) est l'espérance de f(X/n), c'est-à-dire la moyenne de f appliquée au nombre de succès de n expériences indépendantes de probabilité x. La convergence simple de Pn(x) vers f(x) pour tout x est une conséquence de la loi faible des grands nombres. En majorant la probabilité de l'écart entre X/n et x, on en déduit la convergence uniforme de Pn vers f.
Théorème de Stone-Weierstrass, version algébrique
Le théorème d'approximation se généralise dans deux directions :
- L'intervalle compact [a, b] peut être remplacé par un espace compact X.
- L'algèbre des fonctions polynomiales peut être remplacée par une autre sous-algèbre A de C(X) à condition qu'elle vérifie une propriété cruciale qui est de séparer les points (en) (un sous-ensemble A de C(X) sépare les points si pour toute paire {x, y} de points de X, il existe une fonction p de A telle que p(x) ≠ p(y)).
Dans ce cadre, le théorème s'écrit[3] :
Théorème — Soient X un espace compact et C(X) l'algèbre de Banach des fonctions continues de X dans ℝ. Une sous-algèbre est dense dans C(X) si (et seulement si) elle sépare les points et contient, pour tout point x de X, une fonction qui ne s'annule pas en x.
Puisque les polynômes sur [a, b] forment une sous-algèbre unifère de C([a, b]) qui sépare les points, le théorème de Weierstrass est une conséquence du théorème ci-dessus.
Le corps des réels peut être remplacé par celui des complexes, à condition de supposer que A est stable par conjugaison[3].
Ce théorème se déduit du théorème de Stone-Weierstrass « version treillis » (ci-dessous) et des deux lemmes suivants.
Lemme 1 — Pour tout réel a > 0, il existe une suite de polynômes qui converge uniformément sur [–a, a] vers la fonction x ↦ |x|.
Lemme 2 — Toute sous-algèbre fermée de C(X) est un treillis.
Fonctions entières
En 1885, Weierstrass[1] avait aussi démontré un théorème analogue pour les fonctions entières (les fonctions holomorphes dans tout le plan complexe), que Torsten Carleman a généralisé en 1927[5], en montrant que toute fonction continue sur R est limite uniforme (sur R) d'une suite de fonctions entières[6]. Suivant une remarque de Marcel Brelot, Wilfred Kaplan (en) a montré que la preuve de Carleman produisait même le résultat suivant :
Applications
Le théorème de Stone-Weierstrass permet de démontrer les quatre propositions suivantes :
- si f est une fonction continue à valeurs réelles définie sur le pavé [a, b] × [c, d] et si ε est réel strictement positif, alors il existe une fonction polynomiale p à deux variables telle que pour tous x dans [a, b] et y dans [c, d], |f(x,y) – p(x,y)| < ε.
- si X et Y sont deux espaces compacts et si f : X×Y → ℝ est une fonction continue alors, pour tout ε > 0, il existe n > 0 et des fonctions continues f1, f2, … , fn sur X et g1, g2, … , gn sur Y telles que ║f – ∑figi║ < ε
- Une mesure bornée sur [a, b] dont tous les moments sont nuls est nulle (cf. Problème des moments). Par exemple, si une fonction intégrable f de [0, 1] dans ℝ est telle quealors f est nulle presque partout (donc partout si elle est continue).
- Si X est un espace métrique compact (donc séparable) alors l'algèbre de Banach C(X) est séparable[9]. Il suffit en effet de choisir dans X une partie Y dénombrable dense, de définir sur X, pour tout élément y de Y, une fonction fy par fy(x) = d(x, y), et de prendre pour A la sous-ℝ-algèbre unifère de C(X) engendrée par ces fy : puisque A est dense dans C(X) d'après le théorème, la sous-ℚ-algèbre unifère engendrée par ces mêmes fy (dénombrable et dense dans A) est dense dans C(X).
- Si f est une fonction continue sur [a;b] alors f admet une primitive sur ce segment. Cette preuve fournit l'existence d'une primitive sans faire intervenir une notion d'intégrale.
Certains résultats valables pour des fonctions continues peuvent être ramenés au cas de fonctions indéfiniment dérivables en utilisant le théorème de Stone-Weierstrass. C'est ainsi qu'on obtient une démonstration du théorème du point fixe de Brouwer en utilisant le théorème de Stokes.
Théorème de Stone-Weierstrass, version treillis
Soit X un espace compact. Un sous-ensemble L de C(X) est appelé un treillis de C(X) si pour deux éléments quelconques f, g de L, les fonctions max(f,g) et min(f,g) appartiennent aussi à L. La version treillis du théorème de Stone-Weierstrass affirme que[3] :
Théorème — Si X est un espace compact avec au moins deux points et si L est un treillis de C(X) tel que, pour tous points distincts x et y de X et tous réels a et b, L contient une fonction f vérifiant f(x) = a et f(y) = b, alors L est dense dans C(X).
Cette version plus générale résulte immédiatement du lemme suivant.
Lemme 3 — Soit L un treillis de C(X). Pour qu'une fonction g de C(X) appartienne à l'adhérence de L, (il faut et) il suffit que pour tous x, y ∈ X et tout ε > 0, il existe une fonction f ∈ L telle que
Notes et références
- (de) Karl Weierstrass, « Über die analytische Darstellbarkeit sogenannter willkürlicher Functionen einer reellen Veränderlichen », Sitz'ber. K. Preuss. Akad. Wiss. Berlin, : I, p. 633-639 et II, p. 789-805.
- Un tel espace est par définition séparé.
- Laurent Schwartz, Topologie générale et analyse fonctionnelle, Hermann, , p. 372-376
- Cette démonstration est due à Henri Lebesgue, qui venait de passer l'agrégation de mathématiques, dans son premier article : Henri Lebesgue, « Sur l'approximation des fonctions », Bulletin des sciences mathématiques, vol. 22, , p. 278-287 (lire en ligne).
- Torsten Carleman, Sur un théorème de Weierstrass, Arkiv. Mat. Astron. Fys., vol. 20, no 4, 1927, p. 1-5.
- Carleman le formule, comme Weierstrass, en termes — plus connus en 1885 — d'une série de fonctions uniformément (car normalement) convergente (Weierstrass 1885, p. 637 : « es convergirt […] die Reihe […] unbedingt und gleichmässig »).
- (en) Wilfred Kaplan, « Approximation by entire functions », Michigan Math. J., vol. 3, no 1, , p. 43-52 (DOI 10.1307/mmj/1031710533, lire en ligne).
- Pinkus 2000, p. 51-54.
- Cf. (en) Charalambos D. Aliprantis et Kim C. Border, Infinite Dimensional Analysis: A Hitchhiker's Guide, Springer, , 3e éd. (ISBN 978-3-540-32696-0, lire en ligne), p. 353, qui démontrent aussi la réciproque : pour tout compact X, si C(X) est séparable alors X est métrisable. En effet, pour tout espace vectoriel normé séparable E, la boule unité du dual E', munie de la topologie faible-*, est métrisable, or pour E = C(X), X s'identifie naturellement à un sous-espace de cette boule.
Voir aussi
Articles connexes
Bibliographie
(en) Allan Pinkus, « Weierstrass and approximation theory », J. Approx. Theory, vol. 107, no 1, , p. 1-66 (DOI 10.1006/jath.2000.3508)
![{\displaystyle \|f\|=\sup _{x\in [a,b]}|f(x)|}](https://img.franco.wiki/i/5dbe733048ca82ed25955dda10885d40b83a99fe.svg)









![{\displaystyle E:\mathbb {R} \to \left]0,+\infty \right[}](https://img.franco.wiki/i/75af2aeecf2d93b910e4f3ea8b1a8c1f35ce33b9.svg)











