Polynôme de Bernstein

Les polynômes de Bernstein pour les premiers ordres sont :

• n = 0

${\displaystyle B_{0}^{0}(x)=1}$

• n = 1

${\displaystyle B_{0}^{1}(x)=1-x,\ B_{1}^{1}(x)=x}$

• n = 2

${\displaystyle B_{0}^{2}(x)=(1-x)^{2},\ B_{1}^{2}(x)=2x(1-x),\ B_{2}^{2}(x)=x^{2}}$

• n = 3

${\displaystyle B_{0}^{3}(x)=(1-x)^{3},\ B_{1}^{3}(x)=3x(1-x)^{2},\ B_{2}^{3}(x)=3x^{2}(1-x),\ B_{3}^{3}(x)=x^{3}}$

Polynômes de Bernstein de degré 3.

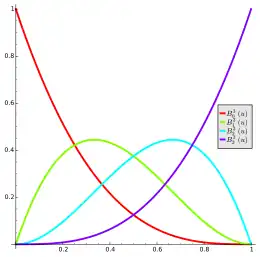
Ces polynômes présentent plusieurs propriétés importantes : ${\displaystyle \forall u\in [0,1]}$

• partition de l'unité :

${\displaystyle \qquad \sum _{i=0}^{m}B_{i}^{m}(u)=1,}$

• positivité :

${\displaystyle \forall i\in \{0,\ldots ,m\}\quad B_{i}^{m}(u)\geq 0,}$

• symétrie :

${\displaystyle \forall i\in \{0,\ldots ,m\}\quad B_{i}^{m}(u)=B_{m-i}^{m}(1-u),}$

• valeurs aux bords :

${\displaystyle \forall i\in \{0,\ldots ,m\}\quad B_{i}^{m}(0)=\delta _{i,0},B_{i}^{m}(1)=\delta _{i,m}}$

avec δ le symbole de Kronecker

• multiplicité des racines :

pour Bm
i, 0 est une racine de multiplicité i et 1, une racine de multiplicité m – i.

• formules de récurrence : pour m > 0,

${\displaystyle B_{i}^{m}(u)={\begin{cases}(1-u)B_{i}^{m-1}(u)&{\text{si }}i=0\\(1-u)B_{i}^{m-1}(u)+uB_{i-1}^{m-1}(u)&\forall i\in \{1,\dots ,m-1\}\\uB_{i-1}^{m-1}(u)&{\text{si }}i=m.\end{cases}}}$.

${\displaystyle B_{i}^{m}\prime (u)=m\left(B_{i-1}^{m-1}(u)-B_{i}^{m-1}(u)\right).}$

• décomposition sur la base canonique :

${\displaystyle B_{i}^{m}(u)={\binom {m}{i}}\sum _{k=0}^{m-i}{\binom {m-i}{k}}(-1)^{k}x^{i+k}=\sum _{l=i}^{m}{\binom {m}{l}}{\binom {l}{i}}(-1)^{l-i}x^{l}}$

et inversement

${\displaystyle u^{p}=\sum _{k=0}^{m-p}{\binom {m-p}{k}}{\frac {1}{\binom {m}{k}}}B_{m-k}^{m}(u)={\frac {1}{\binom {m}{p}}}\sum _{s=p}^{m}{\binom {s}{p}}B_{s}^{m}(u).}$