Polynôme minimal des valeurs spéciales trigonométriques

En mathématiques, et plus précisément en algèbre, on peut chercher à calculer le polynôme minimal d'un nombre de la forme $cos(r π)$ , $sin(r π)$ ou $tan(r π)$ avec $r$ rationnel, que nous appelons dans cet article une « valeur spéciale trigonométrique ».

Dans le polygone régulier convexe à n côtés, l'angle au centre est de mesure 2a avec a =

π

/n.

Le polynôme minimal d'un nombre algébrique $a$ est le polynôme unitaire à coefficients rationnels de plus petit degré dont $a$ est racine.

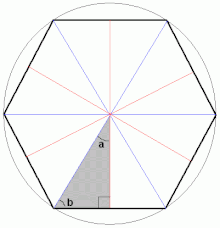
Les mesures d'angles de la forme $r π$ se rencontrent dans de nombreux problèmes géométriques ; en particulier, les mesures d'angles de la forme ${\frac {2\pi }{n}}$ (pour tout entier $n \geq 3$ ) correspondent aux angles au centre des polygones réguliers convexes.

Approche intuitive

Pour établir que

\cos(30^{\circ })={\frac {\sqrt {3}}{2}}

, on peut s'aider d'un triangle équilatéral.

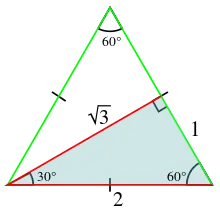
Lorsque l'on apprend la trigonométrie, on constate vite que le cosinus et le sinus des mesures de certains angles ont une forme particulière, qui fait intervenir des racines carrées. Ainsi, pour un angle de mesure 30 degrés, soit $π/6$ radians, le théorème de Pythagore permet de démontrer que :

\cos {\frac {\pi }{6}}={\frac {\sqrt {3}}{2}}

Cela revient à dire que $cos(π/6)$ est une des solutions de l'équation $x^{2}-{\frac {3}{4}}=0$ . L'autre solution de cette équation est $cos(5π/6)$ , qui est aussi de la forme $cos(r π)$ .

L'équation $x^{2}-{\frac {3}{4}}=0$ est polynomiale : elle s'exprime sous la forme $P (x) = 0$ , où $P$ est un polynôme. Comme $P$ est à coefficients rationnels, ses racines sont des nombres algébriques. De plus, $P$ est unitaire, c'est-à-dire que son coefficient dominant vaut 1, et irréductible sur $\mathbb {Q}$ , c'est-à-dire qu'il ne peut pas être factorisé en un produit de polynômes à coefficients rationnels[Note 1]. $P$ est donc de degré minimal parmi les polynômes à coefficients rationnels qui s'annulent en $cos(π/6)$ : c'est son polynôme minimal.

Les questions qui viennent naturellement sont :

quelle est la façon la plus pertinente d'écrire un multiple rationnel de π ?
La réponse[Note 2] est :
- ${\frac {2k\pi }{n}}$ si l'on s'intéresse à son cosinus,
- ${\frac {k\pi }{n}}$ si l'on s'intéresse à son sinus ou à sa tangente ;
son cosinus, son sinus et sa tangente sont-ils algébriques ?
La réponse est oui ;
peut-on toujours les exprimer à l'aide de racines carrées ?
La réponse est cette fois non ;
peut-on tout du moins toujours les exprimer à l'aide de racines n-ièmes ?
La réponse est oui si l'on s'autorise à travailler dans les nombres complexes ;
comment trouve-t-on les polynômes minimaux de ces nombres ?

On verra aussi que l'on peut réduire le degré de ces polynômes, quitte à ne plus travailler seulement avec des polynômes à coefficients rationnels.

Nature algébrique des valeurs spéciales trigonométriques

Le théorème

Théorème — Pour tout rationnel $r$ , les réels $cos(r π)$ , $sin(r π)$ et (si $cos(r π) \neq 0$ ) $tan(r π)$ sont algébriques.

Démonstration

On remarque d'abord que les deux exponentielles $\operatorname {e} ^{\mathrm {i} {\frac {2k\pi }{n}}}$ et $\operatorname {e} ^{-\mathrm {i} {\frac {2k\pi }{n}}}$ (avec $k$ et $n$ entiers) sont algébriques, en tant que racines $n$ -ièmes de l'unité. Comme l'ensemble des nombres algébriques, muni de l'addition et de la multiplication, est un corps, on en déduit que les trois nombres

\cos {\frac {2k\pi }{n}}={\frac {\operatorname {e} ^{\mathrm {i} {\frac {2k\pi }{n}}}+\operatorname {e} ^{-\mathrm {i} {\frac {2k\pi }{n}}}}{2}},\quad \sin {\frac {2k\pi }{n}}={\frac {\operatorname {e} ^{\mathrm {i} {\frac {2k\pi }{n}}}-\operatorname {e} ^{-\mathrm {i} {\frac {2k\pi }{n}}}}{2\operatorname {e} ^{\mathrm {i} {\frac {\pi }{2}}}}}\quad {\text{et}}\quad \tan {\frac {k\pi }{n}}={\frac {\sin {\frac {k\pi }{n}}}{\cos {\frac {k\pi }{n}}}}

sont algébriques.

Cette démonstration est courte mais utilise principalement le fait que l'ensemble des nombres algébriques est stable par somme et produit, ce qui est difficile à démontrer. On peut lui préférer une preuve utilisant des outils plus élémentaires (voir infra).

Degré algébrique

Le degré d'un nombre algébrique est le degré de son polynôme minimal. Derrick Lehmer a calculé le degré de $cos(2 k π/ n)$ [1] - [2] - [3] :

si $n > 2$ et $k$ sont premiers entre eux,

le degré de $cos(2 k π/ n)$ vaut $φ (n)/2$ [Note 3],

où $φ$ est la fonction indicatrice d'Euler. La démonstration[Note 4] utilise simplement l'irréductibilité du $n$ -ième polynôme cyclotomique (voir infra).

Grâce à l'identité trigonométrique $\sin \theta =\cos \left({\frac {\pi }{2}}-\theta \right)$ , on en déduit facilement[Note 5] que

le degré de sin(kπ/n) vaut[4] :
- $φ (n)$ n'est pas divisible par 4 ;
- $φ (n)/4$ si n est un multiple impair de 4;
- $φ (n)/2$ sinon, i.e. si n est un multiple de 8.

Quant au degré de $tan(k π/ n)$ , si $n > 4$ et $k$ et $n$ sont premiers entre eux, il vaut[5] - [4] :

$φ (n)/2$ si $n$ est divisible par 4 ;
$φ (n)$ sinon.

Rationalité

Les rationnels étant les nombres algébriques de degré 1, un corollaire[Note 6] - [6] de la section précédente est que pour les angles multiples rationnels de $π$ , les seules valeurs rationnelles des fonctions trigonométriques usuelles sont :

pour $cos$ et $sin$ [7] : $0$ , $\pm$ $1 / 2$ et $\pm1$ ;
pour $tan$ [8] : $0$ et $\pm1$ .

Expression des valeurs spéciales trigonométriques à l'aide de radicaux

Expression avec des racines carrées

Le polygone régulier à $n$ sommets est constructible (à la règle et au compas) si et seulement si $φ (n)$ est une puissance de 2. En effet, son angle au centre est ${\frac {2\pi }{n}}$ , or un corollaire du théorème de Wantzel affirme que si un nombre est constructible alors son degré est une puissance de $2$ , et la réciproque est fausse en général mais vraie pour les « valeurs spéciales trigonométriques ».

Gauss a donné dès 1796 (sous une forme plus explicite) cette condition suffisante sur l'entier $n$ pour que le polygone régulier à $n$ sommets soit constructible, affirmant qu'elle est aussi nécessaire, ce que Wantzel a confirmé : c'est le théorème de Gauss-Wantzel.

Par exemple, l'heptagone régulier, l'ennéagone régulier et le hendécagone régulier ne sont pas constructibles car $φ (7) = φ (9) = 6$ et $φ (11) = 10$ , tandis que pour les autres valeurs de $n$ de $3$ à $12$ , le $n$ -gone régulier est constructible, comme l'explicite le tableau suivant (pour plus de valeurs de $n$ , voir cette table pour $φ (n)$ et cet article pour les valeurs spéciales trigonométriques exprimables avec des racines carrées).

$n$	$φ (n)$	$cos(2π/ n)$	$sin(π/ n)$	$tan(π/ n)$
12	4	${\frac {\sqrt {3}}{2}}$	${\frac {{\sqrt {3}}-1}{2{\sqrt {2}}}}$	$2-{\sqrt {3}}$
10	4	${\frac {{\sqrt {5}}+1}{4}}$	${\frac {{\sqrt {5}}-1}{4}}$	${\sqrt {1-{\frac {2}{\sqrt {5}}}}}$
8	4	${\frac {1}{\sqrt {2}}}$	${\frac {\sqrt {2-{\sqrt {2}}}}{2}}$	${\sqrt {2}}-1$
6	2	${\frac {1}{2}}$	${\frac {1}{2}}$	${\frac {1}{\sqrt {3}}}$
5	4	${\frac {{\sqrt {5}}-1}{4}}$	${\sqrt {\frac {5-{\sqrt {5}}}{8}}}$	${\sqrt {5-2{\sqrt {5}}}}$
4	2	$0$	${\frac {1}{\sqrt {2}}}$	$1$
3	2	$-{\frac {1}{2}}$	${\frac {\sqrt {3}}{2}}$	${\sqrt {3}}$

Expression avec des racines n-ièmes

Le polynôme minimal de $2cos(2π/7)$ est[Note 4] $X 3 + X 2 - 2 X - 1$ , dont les deux autres racines sont $2cos(4π/7)$ et $2cos(6π/7)$ . Comme ces trois racines sont réelles, on est dans le casus irreducibilis, qui ne peut justement se résoudre dans les nombres réels qu'en repassant par la trigonométrie. Cela explique qu'on ne trouvera jamais une expression de $cos(2π/7)$ avec des racines carrées ou cubiques réelles dans un formulaire de trigonométrie : on ne peut qu'en donner une valeur approchée, ou indiquer son polynôme minimal, dont il est la seule racine positive.

Pourtant, une expression par radicaux de $cos(2π/7)$ existe, à condition d'autoriser l'emploi de racines carrées et cubiques de nombres complexes ; cette expression est donnée par la méthode de Cardan[Note 7] :

\cos {\frac {2\pi }{7}}={\frac {1}{6}}\left({\sqrt[{3}]{\frac {7+21{\sqrt {-3}}}{2}}}+{\sqrt[{3}]{\frac {7-21{\sqrt {-3}}}{2}}}-1\right)

Il en va de même pour $cos(π/9)$ [3], lui aussi algébrique de degré 3.

Qu'en est-il pour les polynômes de degré plus élevé encore ? Abel et Galois ont montré qu'il est impossible d'exprimer en général les racines d'un polynôme de degré 5 ou plus par radicaux. Nous avons vu cependant, dans la section précédente, que certaines valeurs de $cos(2π/ n)$ , de degrés aussi grands qu'on veut, s'expriment par racines carrées donc par radicaux (voir par exemple l'expression de $cos(π/2 m +1)$ , de degré $φ (2 m +2)/2 = 2 m$ ).

En fait, $cos(2π/ n)$ possède toujours une expression par radicaux (de nombres complexes)[9] - [10], puisque le groupe de Galois de son polynôme minimal est abélien donc résoluble (il est isomorphe à (ℤ/nℤ)^×/{1, –1}, comme quotient du groupe de Galois de la $n$ -ième extension cyclotomique par le sous-groupe d'ordre 2 engendré par la conjugaison). Plus simplement, $cos(r π)$ , $sin(r π)$ et $tan(r π)$ (avec $r$ rationnel) peuvent toujours s'exprimer trivialement par radicaux (complexes), puisque $\operatorname {e} ^{\mathrm {i} r\pi }$ est une racine de l'unité.

Polynômes à coefficients non rationnels

Considérons[Note 8] les quatre réels $cos k π / 12 = cos 2 k π / 24$ (pour $k$ premier avec $12$ ), de degré $φ (24) / 2 = 4$ . On les calcule facilement[3] :

\cos {\frac {\pi }{12}}={\frac {{\sqrt {6}}+{\sqrt {2}}}{4}},\quad \cos {\frac {5\pi }{12}}={\frac {{\sqrt {6}}-{\sqrt {2}}}{4}},\quad \cos {\frac {7\pi }{12}}=-\cos {\frac {5\pi }{12}},\quad \cos {\frac {11\pi }{12}}=-\cos {\frac {\pi }{12}}

$cos π / 12$ est par conséquent racine des trois polynômes suivants, du second degré, à coefficients fatalement non tous rationnels :

$\left(X-\cos {\frac {\pi }{12}}\right)\left(X-\cos {\frac {5\pi }{12}}\right)=X^{2}-{\frac {\sqrt {6}}{2}}X+{\frac {1}{4}}=P_{1}({\sqrt {6}},X)$ ;
$\left(X-\cos {\frac {\pi }{12}}\right)\left(X-\cos {\frac {7\pi }{12}}\right)=X^{2}-{\frac {\sqrt {2}}{2}}X-{\frac {1}{4}}=P_{2}({\sqrt {2}},X)$ ;
$\left(X-\cos {\frac {\pi }{12}}\right)\left(X-\cos {\frac {11\pi }{12}}\right)=X^{2}-{\frac {2+{\sqrt {3}}}{4}}=P_{3}({\sqrt {3}},X)$ ;

et le polynôme minimal $P$ peut se factoriser de trois façons :

P(X)=P_{1}({\sqrt {6}},X)P_{1}(-{\sqrt {6}},X)=P_{2}({\sqrt {2}},X)P_{2}(-{\sqrt {2}},X)=P_{3}({\sqrt {3}},X)P_{3}(-{\sqrt {3}},X)

Les six facteurs du second degré sont à coefficients dans un corps quadratique $\mathbb {Q} ({\sqrt {d}})$ ( $d$ égal à 6, 2 ou 3), c'est-à-dire la forme $a + b \sqrt d$ , avec $a$ et $b$ rationnels.

On trouve trois factorisations parce que le groupe de Galois de $P$ , (ℤ/24ℤ)^×/{1, –1}, est isomorphe à (ℤ/8ℤ)^× donc au groupe de Klein, qui a trois sous-groupes d'indice 2.

Dans le cas général $cos(2 k π/ n)$ (avec $n > 2$ et $k$ et $n$ premiers entre eux), on trouvera au moins une factorisation de ce type (produit de deux polynômes à coefficients dans un même corps quadratique et de degré $φ (n)/4$ ) si (et seulement si) $φ (n)$ est divisible par 4. Il n'y en aura qu'une si (ℤ/nℤ)^×/{1, –1} est cyclique.

Calculer le polynôme minimal à coefficients rationnels

Quelques polynômes annulateurs

Pour tout rationnel $r$ , il est facile[Note 9] de trouver un polynôme annulateur de $cos(r π)$ , $sin(r π)$ ou $tan(r π)$ .

Pour $cos(2 k π/ n)$ , on déduit de la formule de Moivre que $\cos(nt)=\Re \left((\cos t+\mathrm {i} \sin t)^{n}\right)=T_{n}(\cos t)$ , où $T n$ est un polynôme de degré $n$ à coefficients entiers (le $n$ -ième polynôme de Tchebychev de première espèce). Or pour $t = 2 k π/ n$ , $cos(nt) = cos(2 k π) = 1$ donc $cos(2 k π/ n)$ est racine du polynôme $T n (X) - 1$ .

On en déduit facilement des polynômes annulateurs de degré $2 n$ pour $sin(k π/ n)$ et $tan(k π/ n)$ , grâce aux formules de l'angle double :

\cos(2\theta )=1-2\sin ^{2}\theta ={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}

Cette seconde démonstration de l'algébricité des « valeurs spéciales trigonométriques » est constructive, car elle fournit une expression d'un polynôme annulateur, c'est-à-dire d'un polynôme $P$ tel que $P (x) = 0$ pour $x = cos(2 k π/ n)$ , $sin(k π/ n)$ ou $tan(k π/ n)$ . Mais vu leurs degrés, les polynômes trouvés par cette méthode ne sont pas minimaux si $n \geq 2$ (voir supra).

On peut souvent construire des polynômes annulateurs de degrés plus petits. Par exemple si $n$ est impair, $n = 2 m + 1$ , on a[Note 9] :

pour $x=\cos {\frac {2k\pi }{n}}\neq 1$ : $1+2\sum _{i=1}^{m}T_{i}(x)=0$ ;
donc pour $y=\sin {\frac {k\pi }{n}}\neq 0$ : $1+2\sum _{i=1}^{m}T_{i}(1-2y^{2})=0$ ;
et pour $z=\tan {\frac {k\pi }{n}}\neq 0$ : $1+2\sum _{i=1}^{m}T_{i}\left({\frac {1-z^{2}}{1+z^{2}}}\right)=0$ ,

ce qui fournit des polynômes annulateurs :

pour $x$ : de degré $n - 1 / 2$ ,
pour $y$ et $z$ : de degré $n - 1$ .

Si $n$ est premier, ils sont même de degré minimum, par identification directe (voir section suivante) ou simplement vu leurs degrés (voir supra)[11].

Polynôme minimal de $cos(2 k π/ n)$

La méthode de Lehmer (voir supra)[12] permet de calculer les polynômes minimaux des $cos(2 k π/ n)$ (pour $k$ et $n$ premiers entre eux) et d'en déduire ceux des $sin(k π/ n)$ . Nous la présentons ici uniquement dans le cas des cosinus[Note 4], sur l'exemple $n = 15$ .

Soit $Φ 15$ le 15^e polynôme cyclotomique usuel :

\Phi _{15}(z)=z^{8}-z^{7}+z^{5}-z^{4}+z^{3}-z+1

$Φ 15$ est de degré $\varphi (15)=8$ . On multiplie $Φ 15 (z)$ par $z^{-{\frac {8}{2}}}$ :

z^{-4}\,\Phi _{15}(z)=(z^{4}+z^{-4})-(z^{3}+z^{-3})+(z+z^{-1})-1

On obtient un nouveau polynôme $Φ 15 (t)$ à coefficients entiers en $t=z+z^{-1}$ , d'après le calcul fourni par les polynômes de Tchebychev :

z^{-4}\,\Phi _{15}(z)=\Theta _{15}(t)=2[T_{4}(t/2)-T_{3}(t/2)+T_{1}(t/2)]-1=(t^{4}-4t^{2}+2)-(t^{3}-3t)+t-1=t^{4}-t^{3}-4t^{2}+4t+1

Variante de calcul

On écrit les puissances de $z+z^{-1}$ de 0 à 4, calculées à l'aide du binôme de Newton, dans un tableau :

{\begin{matrix}(z+z^{-1})^{4}=&z^{4}&&+4z^{2}&&+6&&+4z^{-2}&&+z^{-4}\\(z+z^{-1})^{3}=&&z^{3}&&+3z&&+3z^{-1}&&+z^{-3}&\\(z+z^{-1})^{2}=&&&z^{2}&&+2&&+z^{-2}&&\\(z+z^{-1})^{1}=&&&&z&&+z^{-1}&&&\\(z+z^{-1})^{0}=&&&&&1&&&&\end{matrix}}

En tâtonnant un peu, on arrive à trouver des coefficients entiers tels qu'en multipliant les puissances de $z+z^{-1}$ par ces entiers, on obtienne l'expression de $z^{-4}\,\Phi _{15}(z)$ après avoir additionné les résultats : les coefficients de $(z+z^{-1})^{4}$ et $(z+z^{-1})^{3}$ doivent être respectivement égaux à 1 et –1 pour donner $(z^{4}+z^{-4})-(z^{3}+z^{-3})$ , puis le coefficient de $(z+z^{-1})^{2}$ doit être égal à –4 pour faire disparaître le terme en $z^{2}+z^{-2}$ qu'on vient d'introduire, etc.

{\begin{matrix}(z+z^{-1})^{4}=&z^{4}&&+4z^{2}&&+6&&+4z^{-2}&&+z^{-4}\\-(z+z^{-1})^{3}=&&-z^{3}&&-3z&&-3z^{-1}&&-z^{-3}&\\-4(z+z^{-1})^{2}=&&&-4z^{2}&&-8&&-4z^{-2}&&\\4(z+z^{-1})^{1}=&&&&4z&&+4z^{-1}&&&\\(z+z^{-1})^{0}=&&&&&1&&&&\\{\text{total}}=&z^{4}&-z^{3}&&+z&-1&+z^{-1}&&-z^{-3}&+z^{-4}\end{matrix}}

Cela a fonctionné parce que les polynômes cyclotomiques sont polynômes palindromiques, c'est-à-dire dont les coefficients sont identiques, qu'on les lise dans l'ordre des termes de degré croissant ou décroissant.

Pour $z=\operatorname {e} ^{\mathrm {i} {\frac {2k\pi }{n}}}$ , on a $z+z^{-1}=2\cos(2k\pi /n)$ . Or par définition, le polynôme cyclotomique $Φ n$ a justement pour racines les complexes $\operatorname {e} ^{\mathrm {i} {\frac {2k\pi }{n}}}$ avec $k$ et $n$ premiers entre eux. Le nombre $cos(2 k π/15)$ est donc racine de :

\Theta _{15}(2x)=16x^{4}-8x^{3}-16x^{2}+8x+1

De plus, puisque $Φ 15$ est irréductible sur $\mathbb {Q}$ , $Θ 15$ l'est aussi.

On en déduit le polynôme minimal commun à $cos(2π/15)$ , $cos(4π/15)$ , $cos(8π/15) = -cos(7π/15)$ et $cos(14π/15) = -cos(π/15)$ :

P(x)={\frac {1}{16}}\Theta _{15}(2x)=x^{4}-{\frac {1}{2}}x^{3}-x^{2}+{\frac {1}{2}}x+{\frac {1}{16}}

Listes de polynômes minimaux

Voici une liste des premiers polynômes minimaux[Note 10] de $cos(2π/ n)$ [13] - [Note 4], $sin(π/ n)$ [Note 5] - [14] et $tan(π/ n)$ [Note 11] - [15] pour $n\geq 3$ :

$n$	$\varphi (n)$	Polynôme minimal $C n$ de $cos(2π/ n)$	Polynôme minimal de $sin(π/ n)$	Polynôme minimal de $tan(π/ n)$
12	4	${\frac {1}{2}}C_{6}(2X^{2}-1)=X^{2}-{\frac {3}{4}}$	${\frac {1}{4}}C_{12}(2X^{2}-1)=C_{24}=X^{4}-X^{2}+{\frac {1}{16}}$	$X^{2}-4X+1$
11	10	$X^{5}+{\frac {1}{2}}X^{4}-X^{3}-{\frac {3}{8}}X^{2}+{\frac {3}{16}}X+{\frac {1}{32}}$	$-{\frac {1}{32}}C_{11}(1-2X^{2})=C_{44}=$ $X^{10}-{\frac {11}{4}}X^{8}+{\frac {11}{4}}X^{6}-{\frac {77}{64}}X^{4}+{\frac {55}{256}}X^{2}-{\frac {11}{1024}}$	$X^{10}-55X^{8}+330X^{6}-462X^{4}+165X^{2}-11$
10	4	$C_{5}(-X)=X^{2}-{\frac {1}{2}}X-{\frac {1}{4}}$	$C_{5}$	$X^{4}-2X^{2}+{\frac {1}{5}}$
9	6	$X^{3}-{\frac {3}{4}}X+{\frac {1}{8}}$	$-{\frac {1}{8}}C_{9}(1-2X^{2})=C_{36}=X^{6}-{\frac {3}{2}}X^{4}+{\frac {9}{16}}X^{2}-{\frac {3}{64}}$	$X^{6}-33X^{4}+27X^{2}-3$
8	4	${\frac {1}{2}}C_{4}(2X^{2}-1)=X^{2}-{\frac {1}{2}}$	${\frac {1}{4}}C_{8}(2X^{2}-1)=C_{16}=X^{4}-X^{2}+{\frac {1}{8}}$	$X^{2}+2X-1$
7	6	$X^{3}+{\frac {1}{2}}X^{2}-{\frac {1}{2}}X-{\frac {1}{8}}$	$-{\frac {1}{8}}C_{7}(1-2X^{2})=C_{28}=X^{6}-{\frac {7}{4}}X^{4}+{\frac {7}{8}}X^{2}-{\frac {7}{64}}$	$X^{6}-5X^{4}+3X^{2}-1$
6	2	$-C_{3}(-X)=X-{\frac {1}{2}}$	$C_{6}$	$X^{2}-{\frac {1}{3}}$
5	4	$X^{2}+{\frac {1}{2}}X-{\frac {1}{4}}$	${\frac {1}{4}}C_{5}(1-2X^{2})=C_{20}=X^{4}-{\frac {5}{4}}X^{2}+{\frac {5}{16}}$	$X^{4}-10X^{2}+5$
4	2	$X$	$C_{8}$	$X-1$
3	2	$X+{\frac {1}{2}}$	$C_{12}$	$-2\left(1+X^{2}\right)C_{3}\left({\frac {1-X^{2}}{1+X^{2}}}\right)=X^{2}-3$

Notes et références

Notes

Contrairement aux polynômes irréductibles sur $\mathbb {R}$ (qui sont de degré 1 ou 2) ou sur $\mathbb {C}$ (de degré 1), des polynômes irréductibles sur $\mathbb {Q}$ (comme $X 4 + 1$ ) existent en tout degré.
Voir « Écriture pertinente d'un multiple rationnel de $π$ » sur Wikiversité.
La fonction indicatrice d'Euler ne prenant que des valeurs paires à partir de $n = 3$ , $φ (n)/2$ est bien entier.
Voir le théorème correspondant dans « Polynôme minimal de $cos(r π)$ » sur Wikiversité, illustré par les exemples $n = 7$ ou $9$ et plus généralement, $n$ puissance d'un nombre premier.
Le polynôme minimal de $sin(π/ n)$ est égal à celui de $\cos {\frac {2\pi }{n/2}}$ si $8\mid n-2k$ et se déduit de celui de $cos(2π/ n)$ sinon : voir « Conséquences pour $sin(r π)$ » sur Wikiversité.
Bien qu'ayant été redémontré de nombreuses fois avant que Niven le mentionne comme simple corollaire, il porte le nom de « théorème de Niven ».
Avec la convention suivante : soit un nombre complexe $z=r\operatorname {e} ^{\mathrm {i} \theta }$ , où $r$ est un nombre réel positif et $θ$ est dans l'intervalle $]-π , π]$ , la racine $n$ -ième « principale » de $z$ est ${\sqrt[{n}]{z}}={\sqrt[{n}]{r}}\operatorname {e} ^{\mathrm {i} \theta /n}$ .
Beaucoup d'autres exemples, dont un plus détaillé que celui-ci, figurent dans « Polynômes annulateurs de nombres de la forme 2cos(2kπ╱n) » sur Wikiversité.
Voir « Polynômes de Tchebychev et polynômes annulateurs » sur Wikiversité.
Voir aussi « Polynômes annulateurs de nombres de la forme 2cos(2kπ╱n) » et « Polynômes annulateurs de nombres de la forme tan(kπ╱n) » sur Wikiversité.
Le polynôme minimal de $tan(k π/ n)$ se déduit de celui de $cos(2 k π/ n)$ par une formule de l'angle double, avec un calcul supplémentaire si $n$ est divisible par 4 : voir « Polynôme minimal de $tan(kπ/n)$ » sur Wikiversité, où les exemples $n = 8, 11, 12$ sont traités.

Références

(en) D. H. Lehmer, « A Note on Trigonometric Algebraic Numbers », Amer. Math. Monthly, n^o 40,‎ 1933, p. 165-166 (JSTOR 2301023). Son théorème 2 sur le degré de $sin(2 k π/ n)$ est faux.
(en) Ivan Niven, Irrational Numbers, Cambridge University Press, 1956 (lire en ligne), p. 37-39.
(en) Skip Garibaldi, « Somewhat More than Governors Need to Know about Trigonometry », Mathematics Magazine, vol. 81, n^o 3,‎ juin 2008, p. 191-200 (lire en ligne).
Pour une formulation plus compliquée mais équivalente, voir par exemple Niven 1956, p. 37-39.
(en) Jack S. Calcut, « Rationality and the Tangent Function », sur Oberlin College.
Niven 1956, p. 41, corollaire 3.12 et notes.
(en) R. S. Underwood, « On the irrationality of certain trigonometric functions », Amer. Math. Monthly, vol. 28, n^o 10,‎ 1921, p. 374-376 (JSTOR 2972160).
(en) R. S. Underwood, « Supplementary note on the irrationality of certain trigonometric functions », Amer. Math. Monthly, vol. 29, n^o 9,‎ 1922, p. 346 (JSTOR 2298729).
(en) Un survol de cette question sur le site de MathOverflow.
(en) Literka, « Mathematical Countryside » en calcule une pour $cos(2 k π/11)$ (de degré 5).
Ou encore, pour $y$ et $x$ , d'après le critère d'Eisenstein : cf. (en) Scott Beslin et Valerio De Angelis, « The Minimal Polynomials of sin (2π/p) and cos (2π/p) », Mathematics Magazine, vol. 77, n^o 2,‎ 2004, p. 146-149 (lire en ligne).
Reproduite par (en) William E. Heierman, « Minimal polynomials for trig functions of angles rationally commensurate with π » [« Polynômes minimaux pour les fonctions trigonométriques d'angles rationnellement commensurables avec π »],‎ 4 juin 2009, qui tente d'en déduire une méthode pour $tan(k π/ n)$ .
Extraite de (en) Wolfdieter Lang, « Minimal Polynomials of cos(2π/n) » ( A181875).
Déduite de (en) Wolfdieter Lang, « Minimal Polynomials of sin(2π/n) » ( A181872), mais se déduit aussi de la colonne « Polynôme minimal de $cos(2π/ n)$ » : cf. note précédente.
En partie ( $n = 8, 9, 10, 12$ ) déduite de (en) Kenneth W. Wegner, « Equations with Trigonometric Values as Roots », Amer. Math. Monthly, vol. 66, n^o 1,‎ 1959, p. 52-53 (JSTOR 2309924) et ( $n = 3, 6, 8, 12$ ) extraite de Calcut, p. 16, mais se déduit aussi de la colonne « Polynôme minimal de $cos(2π/ n)$ » : cf. note précédente.

Voir aussi

Bibliographie

(en) Peter Brown, The circle dividers, Parabola, vol. 36, n^o 1, 2000
(en) David Surowski et Paul McCombs, « Homogenous polynomials and the minimal polynomial of $cos(2π/ n)$ », Missouri Journal of Mathematical Sciences, vol. 15, n^o 1,‎ 2003, p. 4-14 (preprint)
(en) William Watkins et Joel Zeitlin, « The minimal polynomial of $cos(2π/ n)$ », Amer. Math. Monthly, vol. 100, n^o 5,‎ 1993, p. 471-474 (JSTOR 2324301)

Lien externe

(en) Eric W. Weisstein, « Trigonometry Angles », sur MathWorld

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.