Idéal de l'anneau des entiers d'un corps quadratique
En mathématiques, les idéaux de l'anneau des entiers d'un corps quadratique ℚ(√d) — cas le plus élémentaire d'un corps de nombres — offrent les premiers exemples de résultats généraux de la théorie algébrique des nombres, comme l'existence d'une décomposition de tout idéal en produit d'idéaux premiers ou la finitude du groupe des classes d'idéaux.
Ces résultats permettent la résolution de certaines équations diophantiennes, comme un cas relativement général de l'équation de Pell-Fermat ou des généralisations du théorème des deux carrés de Fermat.
Contexte
Un corps quadratique est une extension quadratique — extension finie de degré 2 — du corps ℚ des rationnels. C'est donc une extension simple, de la forme K = ℚ(√d) où d est entier sans facteur carré (non nécessairement positif), admettant deux plongements dans le corps ℂ des complexes.
Dans K, les « entiers » (algébriques) sont les racines de polynômes unitaires à coefficients dans l'anneau ℤ des entiers (relatifs). Ce sont des entiers quadratiques et ils forment un sous-anneau du corps. Cet anneau est noté OK, ou parfois ℤ[ω], car il est engendré par un élément ω, égal à (1 + √d)/2 si d est congru à 1 modulo 4 et à √d sinon.
Le début de cet article concerne plus généralement les sous-anneaux unitaires de ℤ[ω] contenant strictement ℤ. Ils sont de la même forme ℤ[ω'], mais pour des ω' plus généraux : pour un certain entier f non carré parfait, de même signe que d et tel que le radical de |f| soit égal à |d|, ω' = √f, ou éventuellement, mais seulement si f est congru à 1 modulo 4, ω' = (1 + √f)/2.
Anneau de Dedekind
Certains anneaux d'entiers quadratiques sont principaux (voire euclidiens). Cette propriété a pour conséquence les théorèmes classiques de l'arithmétique : identité de Bézout, lemme d'Euclide ou encore théorème fondamental de l'arithmétique.
Mais beaucoup ne sont pas principaux ni même factoriels[1]. Ernst Kummer, confronté à cette difficulté, découvre la notion de nombres idéaux (en), qui lui permet de démontrer le dernier théorème de Fermat dans les cas où l'exposant est un nombre premier régulier. Cette approche, finalisée par Richard Dedekind[2], permet d'offrir un palliatif à cette absence de factorialité. Si les éléments de l'anneau ne peuvent plus se décomposer en produit d'éléments premiers, en un certain sens les idéaux le peuvent.
Anneau intégralement clos
Le corps des fractions de tous les sous-anneaux ℤ[ω'] de OK est K et par construction, le seul d'entre eux qui est intégralement clos est OK (un anneau A est dit intégralement clos si ses éléments sont les seuls éléments entiers sur A de son corps des fractions). Mais les deux autres propriétés utiles des sections suivantes sont vraies pour tous les ℤ[ω'].
Anneau noethérien
Dans ℤ, tout élément non nul et non inversible est produit d'un nombre fini d'éléments irréductibles. Cette propriété est vraie (avec unicité de la décomposition) dans tout anneau factoriel, mais l'anneau des entiers d'un corps quadratique n'est pas toujours factoriel. Cependant, elle est vraie aussi (sans l'unicité) dans tout anneau (commutatif, unitaire, intègre) noethérien. Un anneau A est dit noethérien si chacun de ses idéaux est de type fini.
Pour tout idéal non nul M de ℤ[ω'] (avec ω' = √f ou (1 + √f)/2 comme précisé ci-dessus), il existe bien une famille finie, constituée de seulement deux éléments, génératrice du ℤ[ω']-module M et même base de ce ℤ-module :
Tout anneau unitaire d'entiers quadratiques est noethérien. Plus précisément, les idéaux non nuls de ℤ[ω'] sont les sous-ℤ-modules libres de rang 2 de la forme
c(ℤa ⊕ ℤ(b + ω')) avec a, b et c entiers tels que 0 ≤ b < a, 0 < c[3] et :
- si ω' = √f : b2 – f multiple de a ;
- si ω' = (1 + √f)/2 : b(b + 1) – (f – 1)/4 multiple de a.
Idéal premier, idéal maximal
En général, les idéaux de ℤ[ω] ne sont pas tous principaux. Cependant, tous les ℤ[ω'] vérifient une propriété usuelle des anneaux principaux :
Tout idéal premier non nul de ℤ[ω'] est maximal.
Cette propriété découle directement de la suivante :
Tout quotient de ℤ[ω'] par un idéal M non nul est fini : si M est de la forme c(ℤa ⊕ ℤ(b + ω')) ci-dessus, ℤ[ω']/M est d'ordre ac2[3].
Plus précisément, si l'idéal non nul M = c(ℤa ⊕ ℤ(b + ω')) est premier alors ac est un nombre premier p (car l'idéal M ⋂ ℤ = acℤ de ℤ est premier) donc M est soit de la forme ℤp ⊕ ℤ(b + ω'), soit égal à pℤ[ω'], et le corps fini ℤ[ω']/M est donc isomorphe soit à Fp, soit Fp2.
Produit d'idéaux
Les anneaux de Dedekind sont ceux qui, sans être nécessairement factoriels, vérifient la « factorialité pour les idéaux ». Plus précisément (cf. article détaillé) :
Théorème — Pour un anneau A (commutatif, unitaire, intègre), les propriétés suivantes sont équivalentes :
- A est de Dedekind, c'est-à-dire que
- tout idéal premier non nul de A est maximal,
- A est noethérien,
- A est intégralement clos ;
- Tout idéal de A est produit d'idéaux premiers ;
- Pour tout idéal non nul M, il existe un idéal non nul N tel que MN soit principal.
De plus, si A est de Dedekind, la décomposition de tout idéal non nul en produit d'idéaux premiers est unique (à l'ordre près des facteurs).
Comme exposé dans les sections précédentes, les propriétés 1 et 2 ci-dessus sont vérifiées par tous les sous-anneaux ℤ[ω'] de ℤ[ω] et la 3 ne l'est que par ℤ[ω]. Par conséquent, seul ce dernier vérifie la propriété de décomposition des idéaux en idéaux premiers.
Par exemple dans A := ℤ[√–3] (strictement inclus dans l'anneau des entiers d'Eisenstein), l'idéal 4A ne possède aucune décomposition en idéaux premiers. Comme tout idéal propre, il est inclus dans un idéal maximal M qui, dans cet exemple, est unique et égal à 2ℤ + (1 + √–3)ℤ. Il est encore strictement inclus dans M2, mais il contient strictement M3.
Idéal
Trace et norme d'un élément
La trace (relative) Tr(α) d'un élément α de ℚ(√d) est définie comme la trace de l'endomorphisme φα : x ↦ αx et sa norme (relative) comme le déterminant de φα. En notant σ la conjugaison dans ℚ(√d), ces deux rationnels sont Tr(α) = α + σ(α) et N(α) = ασ(α), et sont entiers si et seulement si α appartient à Oℚ(√d).
Norme d'un idéal
La norme d'un idéal non nul M de ℤ[ω'] est définie comme la valeur absolue du déterminant, dans une base du ℤ-module ℤ[ω'], d'une base du sous-module M (cette définition ne dépend pas des bases car les matrices de passages appartiennent à GL(2,ℤ) donc leurs déterminants valent ±1). On démontre alors (cf. article détaillé) :
La norme d'un idéal non nul M de ℤ[ω'] est l'ordre du quotient ℤ[ω']/M.
C'est d'ailleurs par cette méthode qu'on a calculé ci-dessus cet ordre, égal à ac2 si M est de la forme c(ℤa ⊕ ℤ(b + ω')).
Puisque la norme d'un idéal principal engendré par un élément α est égale[4] à la valeur absolue de la norme de α, on en déduit :
La valeur absolue de la norme d'un élément non nul α de ℤ[ω'] est l'ordre du quotient ℤ[ω']/αℤ[ω'].
Cette propriété peut s'interpréter géométriquement en disant que le nombre de points du réseau ℤ[ω'] qui appartiennent à un domaine fondamental du sous-réseau αℤ[ω'] est égal à l'aire relative de ce domaine fondamental : cf. § « Covolume » de l'article « Réseau (géométrie) ».
La norme des éléments est multiplicative par définition. La norme des idéaux l'est aussi (cf. article détaillé) :
La norme du produit de deux idéaux non nuls est égale au produit des normes de ces idéaux.
On sait déjà que l'anneau ℤ[ω] = Oℚ(√d) est de Dedekind (contrairement à ses sous-anneaux non triviaux), mais on peut à présent expliciter la dernière des trois caractérisations équivalentes du § « Produit d'idéaux », car l'identité N(α) = ασ(α) s'étend aux idéaux :
Dans Oℚ(√d), le produit d'un idéal M par son conjugué σ(M) est principal : c'est l'idéal engendré par leur norme commune N(M)[5].
Par exemple dans Oℚ(√–5), le produit de (7, 4 + √–5) par son conjugué est égal à (7).
Discriminant
Pour tout idéal M de ℤ[ω'], l'application (x, y) ↦ xy est une forme bilinéaire sur ce ℤ-module, appelée forme trace. Son déterminant ne dépend pas de la base choisie pour le ℤ-module, ce qui permet de définir le discriminant d'un idéal M comme le déterminant (dans n'importe quelle base) de la forme trace de M.
Pour M = ℤ[ω'], cette définition donne (cf. exemple 2 de l'article détaillé) :
Le discriminant de ℤ[ω'] est égal à f si ω' = (1 + √f)/2 et à 4f si ω' = √f. En particulier :
Le discriminant d'un idéal M de ℤ[ω'] est égal au carré de la norme de M que multiplie le discriminant de ℤ[ω'] :
.
Les définitions et cette proposition sont générales à tout anneau de Dedekind.
Groupe des classes
Le groupe des classes d'un anneau de Dedekind (commutatif) A est le quotient du monoïde des idéaux non nuls de A (muni de la multiplication, avec A comme élément neutre) par la relation d'équivalence
(Ce quotient est bien un groupe (commutatif), d'après la dernière des trois caractérisations équivalentes ci-dessus des anneaux de Dedekind ; pour A = ℤ[ω], l'inverse de la classe de M est la classe de σ(M) : cf. § « Norme d'un idéal ».)
Pour démontrer la proposition suivante (pour l'anneau des entiers de n'importe quel corps de nombres dans l'article détaillé, et pour le cas particulier d'un corps quadratique ici), on utilise des arguments géométriques, un peu de même nature que ceux utilisés plus haut pour interpréter la norme d'un élément :
Toute classe d'idéaux de Oℚ(√d) contient au moins un idéal de norme inférieure ou égale à la constante m définie par l'égalité suivante :
.
On en déduit :
Théorème — Le groupe des classes de Oℚ(√d) est fini.
En effet, chaque classe d'idéaux contient un idéal non nul de norme inférieure ou égale à m, et le nombre de ces idéaux est majoré par le nombre de triplets (a, b, c) d'entiers tels que 0 < ac2 ≤ m et 0 ≤ b < a. Par exemple pour d = –5, toute classe contient un idéal de norme inférieure à 4√5/π ≈ 2,8 et l'idéal de norme 2 est non principal, donc le groupe des classes est d'ordre 2[7]. On peut de plus remarquer que d = –1, –2, –3 et –7 (correspondant à m < 2) font bien partie des valeurs pour lesquelles Oℚ(√d) est principal (et même, en fait, de celles pour lesquelles il est euclidien).
Décomposition des nombres premiers
D'après les sections précédentes :
- tout idéal premier M de ℤ[ω] contient un idéal de la forme pℤ[ω] où p est un nombre premier, unique car
- inversement, d'après les propriétés de la norme, pour tout nombre premier p, tout éventuel idéal M de norme p est premier et vérifie : pℤ[ω] = Mσ(M). Par unicité de la factorisation en idéaux premiers, M et σ(M) sont alors les deux seuls idéaux de norme p s'ils sont distincts, ou M est le seul si σ(M) = M, et
- si pℤ[ω] = Mσ(M) avec σ(M) ≠ M — on dit dans ce cas que p est décomposé — alors d'après le théorème chinois généralisé, ℤ[ω]/pℤ[ω] ≃ ℤ[ω]/M × ℤ[ω]/σ(M) ≃ Fp × Fp ;
- si pℤ[ω] = M2 — on dit dans ce cas que p est ramifié — alors ℤ[ω]/pℤ[ω] ≃ Fp[X]/(X2).
Les idéaux premiers s'obtiennent donc comme les facteurs dans ℤ[ω] des nombres premiers (plus précisément : des idéaux principaux engendrés par ces nombres), et l'on peut prévoir le comportement de chacun d'eux :
Soit P le polynôme minimal de ω (égal à X2 – X – (d – 1)/4 si d ≡ 1 mod 4 et à X2 – d sinon). Dans ℤ[ω], un nombre premier p est :
- inerte si P n'a pas de racine dans Fp ;
- décomposé si P a deux racines distinctes dans Fp ;
- ramifié si P a une racine double dans Fp.
En effet, le comportement de p est donné par le type d'isomorphisme de ℤ[ω]/pℤ[ω], or ℤ[ω] ≃ ℤ[X]/(P) donc ℤ[ω]/pℤ[ω] ≃ ℤ[X]/(p, P) ≃ Fp[X]/(P) (en notant P la réduction mod p de P), et le type d'isomorphisme de Fp[X]/(P) correspond bien, dans chacun des trois cas, à celui calculé pour ℤ[ω]/pℤ[ω]. Ce raisonnement montre de plus que lorsque pℤ[ω] n'est pas premier, il est le produit de l'idéal premier (p, ω – c) par son conjugué, où c est une racine de P dans Fp.
Si p ≠ 2, le comportement est donc déterminé par le discriminant de P, égal au discriminant ∆ de ℤ[ω] (rappelons que ∆ = d ou 4d) : p est inerte si ∆ n'est pas un carré mod p, décomposé si ∆ est un carré non nul mod p, et ramifié si ∆ est divisible par p. La loi de réciprocité quadratique permet ensuite, connaissant les carrés modulo chaque facteur premier de ∆, de déterminer à quelle réunion de classes mod ∆ doit appartenir p pour que ∆ soit un carré mod p.
Si p = 2, l'étude directe de P dans F2[X] montre que p est inerte si d ≡ 5 mod 8, décomposé si d ≡ 1 mod 8 et ramifié sinon.
Remarquons que pour tout p, le cas ramifié était prévisible par un théorème général à l'anneau des entiers de tout corps de nombres : un nombre premier est ramifié si et seulement s'il divise le discriminant de l'anneau.
Notes et références
- Ces deux notions sont en fait équivalentes pour un anneau de Dedekind, or l'anneau des entiers de tout corps de nombres est de Dedekind.
- Richard Dedekind, Traité sur la théorie des nombres trad. C. Duverney, Tricorne, Genève, 2006 (ISBN 2829302893).
- (en) Henri Cohen, A Course in Computational Algebraic Number Theory, coll. « GTM » (no 138), , 4e éd. (1re éd. 1993) (lire en ligne), p. 225, prop. 5.2.1.
- En utilisant (α, αω') comme base de ce ℤ-sous-module si α ≠ 0, et en convenant que la norme de l'idéal nul est 0. Voir aussi Pierre Samuel, Théorie algébrique des nombres [détail de l’édition], p. 62.
- Cf. (en) Keith Conrad, « Factoring in quadratic fields », p. 13. Cette propriété se généralise à tout corps de nombres ((en) David Hilbert, The Theory of Algebraic Number Fields, Springer Verlag, , 351 p. (ISBN 978-3-540-62779-1, lire en ligne), p. 34), en particulier aux corps cyclotomiques ((en) Paulo Ribenboim, 13 Lectures on Fermat's Last Theorem, Springer, , 302 p. (ISBN 978-0-387-90432-0, lire en ligne), p. 80).
- Les démonstrations s'inspirent de Bas Edixhoven et Laurent Moret-Bailly, « Théorie algébrique des nombres », sur université de Rennes I, (cours de maîtrise de mathématiques), chap. 8.
- Cet exemple est détaillé dans Edixhoven et Moret-Bailly 2004, p. 56 et dans (en) Scott T. Chapman, Felix Gotti et Marly Gotti, « How do elements really factor in ℤ[√–5]? », dans Ayman Badawi et Jim Coykendall, Advances in Commutative Algebra: Dedicated to David F. Anderson, Springer, (arXiv 1711.10842), p. 171-196.
Voir aussi
Bibliographie
- (en) David A. Cox, Primes of the Form x2 + ny2, Wiley, (1re éd. 1989) (ISBN 978-1-11803100-1, lire en ligne)
- G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »] [détail de l’édition]
- (en) Kenneth Ireland et Michael Rosen, A Classical Introduction to Modern Number Theory, coll. « GTM » (no 84), (réimpr. 1998), 2e éd., 389 p. (ISBN 978-0-387-97329-6, lire en ligne)
- Jean-Pierre Serre, Cours d'arithmétique, [détail des éditions]
Articles connexes
Lien externe
(en) Eric W. Weisstein, « Quadratic Field », sur MathWorld

![{\displaystyle {\text{discr}}(\mathbb {Z} [\omega ])=\left|{\begin{matrix}1&\omega \\1&\sigma (\omega )\end{matrix}}\right|^{2}={\begin{cases}d&{\text{si }}d\equiv 1{\pmod {4}},\\4d&{\text{sinon.}}\end{cases}}}](https://img.franco.wiki/i/dd59d165208f4dabac69692f799ce8b3b5426569.svg)
![{\displaystyle {\text{discr}}(M)={\mathcal {N}}(M)^{2}~{\text{discr}}(\mathbb {Z} [\omega '])}](https://img.franco.wiki/i/e5e1ee85243519292e03c163df3f0b1b0a8c5f8e.svg)
![{\displaystyle {\text{Si}}\quad d>0,\quad m={\frac {\sqrt {\operatorname {discr} (\mathbb {Z} [\omega ])}}{2}}\quad {\text{et si}}\quad d<0,\quad m={\frac {2}{\pi }}{\sqrt {|\operatorname {discr} (\mathbb {Z} [\omega ])|}}}](https://img.franco.wiki/i/e9bfa67da178a2d4f7a49793594f16b2c24a5c1f.svg)

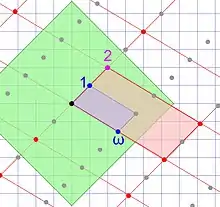
![{\displaystyle 2r^{2}=4~{\mathcal {N}}(J)~{\sqrt {{\text{discr}}\;(\mathbb {Z} [\omega ])}}\quad {\text{donc}}\quad r=\left(2~{\mathcal {N}}(J)~{\sqrt {{\text{discr}}\;(\mathbb {Z} [\omega ])}}\right)^{\frac {1}{2}}}](https://img.franco.wiki/i/769eacf44c3382bcc0c44894260ff5f14ae010c4.svg)

![{\displaystyle |{\mathcal {N}}(\pi )|\leq {\frac {1}{2}}~{\mathcal {N}}(J)~{\sqrt {\operatorname {discr} (\mathbb {Z} [\omega ])}}}](https://img.franco.wiki/i/8625fdea32c6492b01f7ab1c7d7a5da31f10fc01.svg)
![{\displaystyle {\mathcal {N}}(K)={\frac {|{\mathcal {N}}(\pi )|}{{\mathcal {N}}(J)}}\leq {\frac {{\frac {1}{2}}~{\mathcal {N}}(J)~{\sqrt {\operatorname {discr} (\mathbb {Z} [\omega ])}}}{{\mathcal {N}}(J)}}={\frac {\sqrt {\operatorname {discr} (\mathbb {Z} [\omega ])}}{2}}}](https://img.franco.wiki/i/42a459c68e1a667fcd5cf984430f180e0bfc00ab.svg)

![{\displaystyle \pi r^{2}=4~{\mathcal {N}}(J)~{\frac {1}{2}}~{\sqrt {|\operatorname {discr} (\mathbb {Z} [\omega ])|}}\quad {\text{donc}}\quad r=\left({\frac {2}{\pi }}~{\mathcal {N}}(J)~{\sqrt {|\operatorname {discr} (\mathbb {Z} [\omega ])}}|\right)^{\frac {1}{2}}}](https://img.franco.wiki/i/d8a0ae0a3b88328ed4e8455086142298d08eb0ff.svg)
![{\displaystyle {\frac {2}{\pi }}~{\mathcal {N}}(J)~{\sqrt {|\operatorname {discr} (\mathbb {Z} [\omega ])}}|}](https://img.franco.wiki/i/009b3ebe7ec4acea0e714f7de7e0c48c70a34015.svg)
![{\displaystyle {\mathcal {N}}(K)\leq {\frac {2}{\pi }}~{\sqrt {|\operatorname {discr} (\mathbb {Z} [\omega ])}}|}](https://img.franco.wiki/i/65c8b2ffaf2f0557b2652026615e09c05a5696ea.svg)