Solution idéale
En chimie physique, une solution est dite solution idéale si les interactions entre les molécules qui composent cette solution, toutes espèces confondues, sont toutes identiques. Autrement dit, les molécules des différentes espèces s'attirent ou se repoussent entre elles de la même façon que les molécules de chaque espèce à l'état pur s'attirent ou se repoussent entre elles. Les solutions idéales peuvent être définies pour n'importe quelle phase (gaz, liquide ou solide).
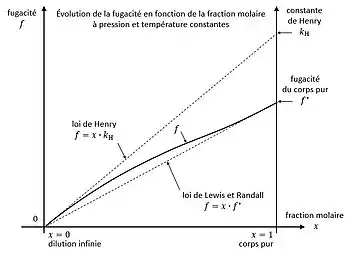
Dans une solution idéale les fugacités des divers corps, à pression et température données, varient linéairement par rapport à leur fraction molaire, par exemple selon la loi de Lewis et Randall ou selon la loi de Henry.
Une solution idéale est formellement définie en thermodynamique par la loi de Lewis et Randall.
Les grandeurs extensives d'une solution idéale ou réelle sont calculées à partir des grandeurs extensives des corps la constituant pris à l'état pur et de grandeurs de mélange qui traduisent la création d'entropie lors d'une opération de mélange.
Définition
Exemples de solutions idéales
Le mélange de gaz parfaits, tel que défini par le théorème de Gibbs, est le modèle de référence de la solution idéale. Ceci est inclus dans la définition même des gaz parfaits : en effet, dans un gaz parfait les interactions entre molécules sont toutes identiques, puisqu'elles sont nulles. Ainsi, dans un mélange d'espèces chimiques différentes à l'état de gaz parfaits toutes les interactions entre les diverses espèces sont nulles. Les mélanges gazeux réels qui se comportent à basse pression comme des gaz parfaits constituent donc des solutions idéales, par exemple l'air à la pression atmosphérique. Le modèle de la solution idéale permet d'étendre les propriétés du mélange de gaz parfaits à tout autre état de la matière (liquide et solide notamment), y compris ceux dans lesquels les interactions entre molécules ne sont pas nulles[3].
Les mélanges liquides réels de molécules de structures et de tailles similaires ont un comportement proche de la solution idéale[3] :
- les mélanges de paraffines linéaires C5 à C8, par exemple de n-heptane et n-octane ;
- les mélanges de benzène, toluène, xylènes ;
- les mélanges d'alcools, par exemple d'éthanol et de propanol.
Le comportement d'une solution liquide dans laquelle le soluté est très dilué est proche de celui d'une solution idéale. Les propriétés colligatives de cette solution peuvent alors être déterminées par plusieurs lois démontrées à l'aide de l'hypothèse de la solution idéale :
- loi de l'ébulliométrie concernant l'élévation du point d'ébullition du solvant ;
- loi de la cryométrie concernant l'abaissement du point de fusion du solvant ;
- loi de la tonométrie concernant l'abaissement de la pression de vapeur saturante du solvant ;
- loi de l'osmométrie concernant l'osmose.
Si une solution liquide idéale est en équilibre avec sa vapeur idéale, alors l'équilibre liquide-vapeur suit la loi de Raoult ou la loi de Henry. La vapeur (gaz en équilibre avec le liquide) est un mélange de gaz parfaits. Au contraire, si l'on mélange 1 litre d'eau avec 1 litre d'éthanol, on obtient un volume total d'environ 1,92 litre[4]. Le volume idéal étant de 2 litres, il y a donc contraction du mélange : les molécules d'eau et d'éthanol s'attirent plus fortement que les molécules de ces liquides purs. Le mélange eau-éthanol n'est donc pas une solution idéale, il présente d'ailleurs un azéotrope que la loi de Raoult est incapable de représenter (néanmoins tous les mélanges non idéaux ne présentent pas nécessairement d'azéotrope).
Le mélange cuivre-nickel (Cu-Ni) peut être considéré comme un mélange idéal, tant en phase liquide qu'en phase solide. Un équilibre liquide-solide idéal suit l'équation de Schröder-van Laar généralisée aux solutions idéales (équivalent pour les équilibres liquide-solide de la loi de Raoult des équilibres liquide-vapeur). Au contraire, les mélanges iodure de potassium-chlorure de potassium (KI-KCl) et or-cuivre (Au-Cu) présentent un point de fusion congruent (équivalent pour les équilibres liquide-solide de l'azéotrope des équilibres liquide-vapeur) qui prouve leur non idéalité[5] (néanmoins tous les mélanges non idéaux ne présentent pas nécessairement de point de fusion congruent).
Loi de Lewis et Randall
Du point de vue de la thermodynamique, une solution en phase (gaz, liquide ou solide), à pression et température , est idéale si la fugacité de chacun de ses constituants répond à la loi de Lewis et Randall (1923) :
| Loi de Lewis et Randall : |
Cette formulation est équivalente à celle donnée par la relation des potentiels chimiques :
avec :
- la pression totale du mélange ;
- la température du mélange ;
- la fraction molaire du constituant ;
- la fugacité du composant dans la solution idéale ;
- la fugacité du composant pur, aux mêmes , et phase que la solution idéale ;
- le potentiel chimique du composant dans la solution idéale ;
- le potentiel chimique du composant pur, aux mêmes , et phase que la solution idéale ; , l'enthalpie libre molaire du corps pur ;
- la constante universelle des gaz parfaits.
Par définition de la fugacité, nous avons les relations :
avec le potentiel chimique du composant à l'état de gaz parfait pur, aux mêmes et que la solution idéale.
Donc en substituant :
dans :
et en considérant que :
on obtient :
Exemple - Les gaz parfaits.
- La fugacité d'un gaz parfait pur est la pression : . La fugacité du même gaz parfait dans un mélange de gaz parfaits, quelle que soit sa fraction molaire , est sa pression partielle : . Un mélange de gaz parfaits est une solution idéale selon la loi de Lewis et Randall.
Cette loi n'est dans les faits vraie, pour les solutions réelles, que pour de fortes concentrations du corps , proches du corps pur.
Extension de la notion de solution idéale
La notion de solution idéale peut être étendue en prenant toute autre référence de concentration que le corps pur[3] :
| Solution idéale : |
avec :
- la fugacité du corps à la concentration , aux pression , température et phase de la solution idéale ;
- une concentration fixe du corps .
Une solution idéale est donc caractérisée, à pression et température données, par une évolution linéaire des fugacités des corps constituant ce mélange en fonction de leurs fractions molaires. La concentration de référence peut être différente d'un corps à un autre[3].
Cette formulation est équivalente à celle donnée par la relation des potentiels chimiques :
avec le potentiel chimique du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
Par définition de la fugacité, nous avons les relations :
avec le potentiel chimique du composant à l'état de gaz parfait pur, aux mêmes et que la solution idéale.
On substitue issue de la deuxième relation dans la première :
puis la relation entre fugacités.
Pour un corps , les états de référence les plus utilisés sont :
- l'état de corps pur, avec et ;
- l'état de dilution infinie dans un corps , avec et ; dans ce cas on a ;
- l'état liquide à une concentration de = 1 mol/l ; le terme est alors remplacé par , avec la concentration molaire du corps en phase liquide.
Le premier état donne la loi de Lewis et Randall. Le deuxième état donne, par la règle de L'Hôpital, la loi de Henry :
avec la constante de Henry du corps infiniment dilué dans le corps , qui est la pente à dilution infinie de la fugacité du corps dans le mélange binaire .
Grandeurs extensives d'une solution idéale
On considère une solution idéale constituée de espèces chimiques différentes sous la pression , à la température et dans une phase donnée (gaz, liquide ou solide). Chaque espèce est représentée par la quantité et la fraction molaire .
Enthalpie libre
L'enthalpie libre et le potentiel chimique sont liés par définition puisque :
- l'enthalpie libre molaire partielle du corps dans la solution idéale ;
- l'enthalpie libre molaire partielle du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
On obtient par définition de la solution idéale la relation :
Le théorème d'Euler sur les fonctions homogènes du premier ordre permet de calculer l'enthalpie libre de la solution idéale selon :
D'où l'enthalpie libre idéale[3] :
| Enthalpie libre idéale : |
Enthalpie
La relation de Gibbs-Helmholtz permet d'écrire pour l'enthalpie :
- l'enthalpie de la solution idéale ;
- l'enthalpie molaire partielle du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
En développant la première relation selon :
D'où l'enthalpie idéale[3] :
| Enthalpie idéale : |
Entropie
Par définition de l'enthalpie et de l'enthalpie libre, nous avons les relations sur l'entropie :
- l'entropie de la solution idéale ;
- l'entropie molaire partielle du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
D'où, étant donné les relations obtenues précédemment pour l'enthalpie et l'enthalpie libre, l'entropie idéale[3] :
| Entropie idéale : |
Volume
Le volume et l'enthalpie libre sont liés par l'une des équations d'état :
- le volume de la solution idéale ;
- le volume molaire partiel du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
En développant la première relation[3] :
D'où le volume idéal :
| Volume idéal : |
En conséquence, si l'on mélange plusieurs liquides, le volume de la solution idéale résultante est la somme des volumes de chacun des liquides purs. Au contraire, si l'on mélange 1 litre d'eau avec 1 litre d'éthanol, on obtient un volume total d'environ 1,92 litre[4]. Le volume idéal étant de 2 litres, il y a donc contraction du mélange : les molécules d'eau et d'éthanol s'attirent plus fortement que les molécules de ces liquides purs. Le mélange eau-éthanol n'est donc pas une solution idéale. Pour les gaz, cette loi correspond à la loi d'Amagat des mélanges de gaz parfaits.
Dans une solution liquide idéale constituée d'un soluté dissout dans un solvant , le soluté répond à la loi de Henry et le solvant à la loi de Lewis et Randall. Le volume idéal vaut :
avec :
- la quantité du soluté ;
- la quantité du solvant ;
- le volume molaire partiel du soluté à dilution infinie dans le solvant liquide ;
- le volume molaire du solvant liquide pur.
Énergie interne
Par définition de l'énergie interne et de l'enthalpie, nous avons les relations :
- l'énergie interne de la solution idéale ;
- l'énergie interne molaire partielle du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
D'où, étant donné les relations obtenues plus haut pour l'enthalpie et le volume, l'énergie interne idéale :
| Énergie interne idéale : |
Énergie libre
Par définition de l'énergie libre, nous avons les relations :
- l'énergie libre de la solution idéale ;
- l'énergie libre molaire partielle du corps à la concentration , aux mêmes pression, température et phase que la solution idéale.
D'où, étant donné les relations obtenues plus haut pour l'énergie interne et l'entropie, l'énergie libre idéale :
| Énergie libre idéale : |
Grandeurs de mélange idéales
La grandeur de mélange idéale exprime l'écart entre la grandeur thermodynamique extensive totale d'une solution idéale et la somme des mêmes grandeurs thermodynamiques extensives des corps pris à leur concentration de référence , aux mêmes quantité, pression, température et phase que la solution idéale :
| Grandeur de mélange idéale : |
On a ainsi :
- l'enthalpie libre de mélange idéale :
- l'enthalpie de mélange idéale :
- l'entropie de mélange idéale :
- le volume de mélange idéal :
- l'énergie interne de mélange idéale :
- l'énergie libre de mélange idéale :
Puisque pour tout corps on a , alors , et . Il y a création d'entropie lors d'une opération de mélange idéale.
Note : ne pas confondre grandeur du mélange idéal et grandeur de mélange idéale .
Grandeurs extensives des solutions réelles
On considère une solution réelle constituée de espèces chimiques différentes sous la pression , à la température et dans une phase donnée (gaz, liquide ou solide). Chaque espèce est représentée par la quantité et la fraction molaire .
Une grandeur extensive d'une solution réelle est calculée à partir de la grandeur extensive équivalente d'une solution idéale à laquelle on ajoute une grandeur extensive (selon le cas grandeur résiduelle ou grandeur d'excès ) représentant l'écart à l'idéalité.
Grandeurs de mélange
La grandeur de mélange exprime l'écart entre une grandeur thermodynamique extensive d'une solution réelle et la somme des mêmes grandeurs thermodynamiques extensives des corps pris à leur concentration de référence , aux mêmes quantité, pression, température et phase que la solution réelle
| Grandeur de mélange : |
Note : ne pas confondre grandeur du mélange et grandeur de mélange .
Cas d'un mélange gazeux
La solution idéale prise comme référence est un mélange de gaz parfaits dont les propriétés sont calculées à partir des propriétés des corps purs à l'état de gaz parfaits aux mêmes pression et température que le mélange gazeux réel. Selon le théorème de Gibbs, un mélange de gaz parfaits est une solution idéale. Les grandeurs extensives d'un mélange gazeux réel sont obtenues en additionnant aux grandeurs extensives du mélange de gaz parfaits les grandeurs résiduelles calculées à partir d'une équation d'état :
avec la grandeur des moles du corps à l'état de gaz parfait pur aux mêmes pression et température que le mélange gazeux réel.
Les grandeurs extensives d'un mélange gazeux réel sont donc calculées selon :
| Grandeurs extensives d'un mélange gazeux réel : |
La grandeur de mélange pour le mélange gazeux réel vaut donc :
En particulier pour l'enthalpie libre , en introduisant la fraction molaire et le coefficient de fugacité de chaque constituant :
- l'enthalpie libre des moles du corps à l'état de gaz parfait pur aux mêmes et que le mélange gazeux réel ;
- l'enthalpie libre de mélange idéale ;
- l'enthalpie libre résiduelle ;
- l'enthalpie libre de mélange ;
on a :
- l'enthalpie libre du mélange gazeux idéal, soit l'enthalpie libre du mélange de gaz parfaits correspondant ;
- l'enthalpie libre du mélange gazeux réel ;
soit :
ou, en notant la fugacité du constituant :
Ainsi, dans une solution gazeuse réelle le potentiel chimique du composant vaut :
avec :
- le potentiel chimique, ou enthalpie libre molaire partielle, du corps dans le mélange gazeux réel aux pression et température ;
- le potentiel chimique, ou enthalpie libre molaire partielle, du corps à l'état de gaz parfait pur aux pression et température ;
- la fugacité du corps dans le mélange gazeux réel ;
- la fraction molaire du corps dans le mélange gazeux réel ;
- le coefficient de fugacité du corps dans le mélange gazeux réel.
Ceci est également applicable aux liquides aux hautes pressions, pour lesquelles les équations d'état telles que celles de Soave-Redlich-Kwong ou Peng-Robinson représentent correctement les phases liquides. Aux basses pressions (moins de 10 bar), l'approche suivante par grandeur d'excès est préférable.
Cas d'un mélange liquide ou solide
Pour une phase liquide, la solution idéale prise comme référence est un mélange dont les propriétés sont calculées à partir des propriétés des corps purs liquides aux mêmes quantités, pression et température que le mélange liquide réel. Les grandeurs extensives du mélange liquide réel sont obtenues en additionnant aux grandeurs extensives du mélange liquide idéal les grandeurs d'excès calculées à partir d'un modèle de coefficients d'activité :
avec la grandeur des moles du corps liquide pur aux mêmes pression et température que le mélange liquide réel.
Les grandeurs extensives d'un mélange liquide réel sont donc calculées selon :
| Grandeurs extensives d'un mélange liquide réel : |
La grandeur de mélange pour le mélange liquide réel vaut donc :
En particulier pour l'enthalpie libre , en introduisant la fraction molaire et le coefficient d'activité de chaque constituant :
- l'enthalpie libre des moles du corps liquide pur aux mêmes et que le mélange liquide réel ;
- l'enthalpie libre de mélange idéale ;
- l'enthalpie libre d'excès ;
- l'enthalpie libre de mélange ;
on a :
- l'enthalpie libre du mélange liquide idéal ;
- l'enthalpie libre du mélange liquide réel ;
soit :
ou, en notant l'activité chimique du constituant :
Ainsi, dans une solution liquide réelle le potentiel chimique du composant vaut :
avec :
- le potentiel chimique, ou enthalpie libre molaire partielle, du corps dans le mélange liquide réel aux pression et température ;
- le potentiel chimique, ou enthalpie libre molaire partielle, du corps à l'état de liquide pur aux pression et température ;
- l'activité du corps dans le mélange liquide réel ;
- la fraction molaire du corps dans le mélange liquide réel ;
- le coefficient d'activité du corps dans le mélange liquide réel.
La même approche est appliquée aux solides, la solution idéale solide étant basée sur les propriétés des corps purs solides aux mêmes pression et température que le mélange réel. Il est alors nécessaire de disposer d'un modèle de coefficients d'activité pour les solides.
Notes et références
Notes
- (en) J. P. O'Connell et J. M. Haile, Thermodynamics : Fundamentals for Applications, Cambridge University Press, (ISBN 978-1-139-44317-3, lire en ligne), p. 435.
- Corriou 1985, p. 25-26.
- Schwartzentruber « Solution idéale ».
- Fiche INRS de l'éthanol.
- Tristan Ribeyre, Chimie : Un accompagnement au quotidien, Louvain-la-Neuve/Paris, De Boeck Supérieur, coll. « PC/PC* Tout-en-un - 2e année », , 1136 p. (ISBN 978-2-8041-8774-3, lire en ligne), p. 21-22.
Bibliographie
- Articles
- E. Darmois, « La thermodynamique des solutions », J. Phys. Radium, vol. 4, no 7, , p. 129-142 (lire en ligne, consulté le ).
- Ouvrages
- Jean-Pierre Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1026, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et cinétique chimique, pack Opérations unitaires. Génie de la réaction chimique, univers Procédés chimie - bio - agro », , p. 1-30.
- Jean-Pierre Corriou, Thermodynamique chimique : Équilibres thermodynamiques, vol. J 1028, Techniques de l'ingénieur, coll. « base documentaire : Thermodynamique et cinétique chimique, pack : Opérations unitaires. Génie de la réaction chimique, univers : Procédés chimie - bio - agro », , p. 1-31.
- Jean Vidal, Thermodynamique : application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », , 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne), p. 159.
Liens externes
- Jacques Schwartzentruber, École nationale supérieure des mines d'Albi-Carmaux, « Solution idéale », sur nte.mines-albi.fr, (consulté le ).
- Jacques Schwartzentruber, École nationale supérieure des mines d'Albi-Carmaux, « L'écart à l'idéalité », sur nte.mines-albi.fr, (consulté le ).











































































































































