Loi de la tonométrie

En chimie physique la loi de la tonométrie permet de quantifier l'abaissement de la pression de vapeur saturante d'un solvant en fonction de la quantité de soluté ajouté.

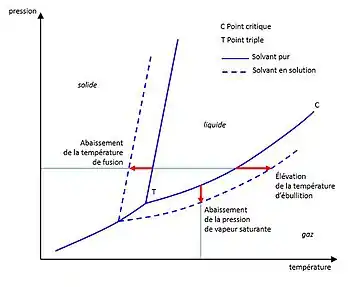
Diagramme de phases d'un solvant pur (courbes pleines) et du même solvant en présence d'un soluté (pointillés). Les propriétés colligatives se traduisent par un déplacement des courbes d'équilibre solide-liquide et gaz-liquide.

Elle est, avec la loi de la cryométrie et la loi de l'ébulliométrie, l'une des trois lois énoncées à partir de 1878 par François-Marie Raoult[1] concernant les propriétés colligatives d'une solution chimique liquide. Avec la loi de l'osmométrie, énoncée par Jacobus Henricus van 't Hoff en 1896 et concernant le phénomène de l'osmose, ces lois ont notamment permis d'établir des méthodes de détermination expérimentale de la masse molaire des espèces chimiques.

Remarque

Lorsque l'on parle des lois de Raoult[2] (au pluriel), on fait généralement allusion aux trois lois évoquées ci-dessus qu'il ne faut pas confondre avec la loi de Raoult (au singulier) concernant les équilibres liquide-vapeur idéaux.

Énoncé de la loi

Cas général

Lorsque l'on considère un solvant $s$ contenant un soluté $\sigma$ , la pression de vapeur saturante du solvant avec le soluté est plus basse que la pression de vapeur saturante du solvant seul à la même température. La loi de la tonométrie s'énonce ainsi :

« Dans une solution binaire, l'abaissement relatif de la pression de vapeur saturante du solvant est égal à la fraction molaire du soluté. »

Soit :

Loi de la tonométrie :

{\Delta P^{\text{sat}} \over P^{\text{sat}}}=x_{\sigma }

avec :

$P^{\text{sat}}$ la pression de vapeur saturante du solvant pur ;
$\Delta P^{\text{sat}}$ l'abaissement absolu de la pression de vapeur saturante du solvant en présence du soluté ;
$x_{\sigma }$ la fraction molaire du soluté.

Le terme ${\Delta P^{\text{sat}} \over P^{\text{sat}}}$ est l'abaissement relatif de la pression de vapeur saturante du solvant.

Autrement dit, à température constante, la pression de vapeur saturante $P^{\text{sat}}$ du solvant pur passe à $P=P^{\text{sat}}-\Delta P^{\text{sat}}$ en présence d'un soluté. La fraction molaire du soluté étant une grandeur positive, l'abaissement de pression est positif. Ainsi l'ajout d'un soluté fait-il diminuer la pression de vapeur saturante du solvant à température constante ( $\Delta P^{\text{sat}}>0$ , soit $P<P^{\text{sat}}$ ).

La loi de la tonométrie a été établie expérimentalement, mais elle peut se démontrer théoriquement. Cette loi n'est valable que sous les hypothèses suivantes :

la quantité de soluté est négligeable devant celle du solvant dans la solution liquide ;
la solution liquide se comporte comme une solution idéale ;
la phase gaz peut être considérée comme constituée de solvant pur, le soluté étant très peu volatil ;
la phase gaz est un gaz parfait, ce qui implique des pressions de l'ordre de la pression atmosphérique ;
le volume molaire de la phase liquide est négligeable par rapport à celui de la phase gaz, ce qui suppose d'être éloigné du point critique du solvant.

En fonction de la molalité

La loi de la tonométrie est souvent exprimée en fonction de la molalité $b_{\sigma }$ du soluté, qui représente la quantité de soluté pour 1 kg de solvant (en mol/kg) :

Loi de la tonométrie :

{\Delta P^{\text{sat}} \over P^{\text{sat}}}={M_{s} \over 1000}\cdot b_{\sigma }

avec $M_{s}$ la masse molaire du solvant (en g/mol).

Démonstration

On note :

$M_{s}$ la masse molaire du solvant (en g/mol) ;
$m_{s}$ la masse de solvant (en g) ;
$n_{s}$ la quantité de solvant (en mol) ;
$n_{\sigma }$ la quantité de soluté (en mol).

On a, par définition de la fraction molaire, pour le soluté :

x_{\sigma }={n_{\sigma } \over n_{s}+n_{\sigma }}

Si la quantité de soluté est négligeable devant celle du solvant :

n_{\sigma }\ll n_{s}

x_{\sigma }\approx {n_{\sigma } \over n_{s}}

La masse de solvant est donnée par :

m_{s}=M_{s}\cdot n_{s}

La molalité du soluté est donnée par définition par :

b_{\sigma }={n_{\sigma } \over m_{s}}={n_{\sigma } \over M_{s}\cdot n_{s}}

On a par conséquent le rapport :

x_{\sigma }\approx M_{s}\cdot b_{\sigma }

La masse molaire étant exprimée le plus souvent en g/mol et la molalité en mol/kg, il est nécessaire d'introduire un facteur de conversion :

x_{\sigma }\approx {M_{s} \over 1000}b_{\sigma }

Pour un soluté dissociatif

Si le soluté se dissocie dans la solution liquide, comme par exemple un sel se dissociant en ions, l'expression de la loi est modifiée par le facteur de van 't Hoff $i$ :

Loi de la tonométrie :

{\Delta P^{\text{sat}} \over P^{\text{sat}}}={M_{s} \over 1000}\cdot i\cdot b_{\sigma }

Démonstration

Pour un solvant pur au point d'ébullition, à température $T$ sous sa pression de vapeur saturante $P^{\text{sat}}$ correspondante, on a l'égalité des potentiels chimiques des deux phases gaz et liquide :

(1)

\mu ^{\text{g,*}}\!\left(P^{\text{sat}}\right)=\mu ^{\text{l,*}}\!\left(P^{\text{sat}}\right)

avec :

$\mu ^{\text{g,*}}$ le potentiel chimique en phase gaz pur ;
$\mu ^{\text{l,*}}$ le potentiel chimique en phase liquide pur.

On introduit, à température $T$ constante, un soluté dans le solvant liquide. La pression de vapeur saturante du solvant est modifiée et devient $P$ . Le potentiel chimique du solvant en phase liquide idéale $\mu ^{\text{l}}$ s'écrit, avec $x_{s}$ la fraction molaire du solvant dans cette phase :

\mu ^{\text{l}}\!\left(P\right)=\mu ^{\text{l,*}}\!\left(P\right)+RT\,\ln x_{s}

On considère qu'en phase gazeuse le solvant est le seul constituant. Au nouvel équilibre de phase on a toujours l'égalité des potentiels chimiques :

\mu ^{\text{g,*}}\!\left(P\right)=\mu ^{\text{l}}\!\left(P\right)

on a donc :

(2)

\mu ^{\text{g,*}}\!\left(P\right)=\mu ^{\text{l,*}}\!\left(P\right)+RT\,\ln x_{s}

En soustrayant les termes de la relation (1) dans la relation (2) on a :

(3)

\mu ^{\text{g,*}}\!\left(P\right)-\mu ^{\text{g,*}}\!\left(P^{\text{sat}}\right)=\mu ^{\text{l,*}}\!\left(P\right)-\mu ^{\text{l,*}}\!\left(P^{\text{sat}}\right)+RT\,\ln x_{s}

La relation de Gibbs-Duhem donne la variation du potentiel chimique du solvant pur à température constante :

\mathrm {d} \mu ^{*}={\bar {V}}^{*}\,\mathrm {d} P

avec ${\bar {V}}^{*}$ le volume molaire du solvant pur. On peut donc intégrer, en considérant une faible variation de pression sur laquelle le volume molaire peut être considéré comme constant :

\int _{P^{\text{sat}}}^{P}\mathrm {d} \mu ^{*}={\bar {V}}^{*}\int _{P^{\text{sat}}}^{P}\mathrm {d} P

\mu ^{*}\!\left(P\right)-\mu ^{*}\!\left(P^{\text{sat}}\right)={\bar {V}}^{*}\cdot \left(P-P^{\text{sat}}\right)

On peut par conséquent réécrire la relation (3) :

{\bar {V}}^{\text{g,*}}\cdot \left(P-P^{\text{sat}}\right)={\bar {V}}^{\text{l,*}}\cdot \left(P-P^{\text{sat}}\right)+RT\,\ln x_{s}

\left({\bar {V}}^{\text{g,*}}-{\bar {V}}^{\text{l,*}}\right)\cdot \left(P-P^{\text{sat}}\right)=RT\,\ln x_{s}

Le volume molaire du liquide étant négligeable devant celui du gaz ${\bar {V}}^{\text{g,*}}\gg {\bar {V}}^{\text{l,*}}$ :

{\bar {V}}^{\text{g,*}}\cdot \left(P-P^{\text{sat}}\right)\approx RT\,\ln x_{s}

En considérant le gaz comme un gaz parfait ${\bar {V}}^{\text{g,*}}=RT/P^{\text{sat}}$ :

{P-P^{\text{sat}} \over P^{\text{sat}}}=\ln x_{s}

Soit $x_{\sigma }=1-x_{s}$ la fraction molaire du soluté. Puisque $x_{\sigma }\approx 0$ , alors $\ln x_{s}=\ln \!\left(1-x_{\sigma }\right)\approx -x_{\sigma }$ par développement limité. On obtient finalement la loi de la tonométrie :

Loi de la tonométrie :

{P^{\text{sat}}-P \over P^{\text{sat}}}=x_{\sigma }

Applications

Tonométrie, détermination de la masse molaire du soluté

La tonométrie[3] est une technique permettant de déterminer la masse molaire d'un soluté.

On introduit une masse $m_{\sigma }$ de soluté dans une masse $m_{s}$ de solvant, on mesure l'augmentation $\Delta P^{\text{sat}}$ de la pression de vapeur saturante du solvant.

Démonstration

On note :

$n_{\sigma }$ la quantité du soluté ;
$n_{s}$ la quantité du solvant ;
$x_{\sigma }$ la fraction molaire du soluté ;
$m_{\sigma }$ la masse du soluté ;
$m_{s}$ la masse du solvant ;
$M_{\sigma }$ la masse molaire du soluté ;
$M_{s}$ la masse molaire du solvant ;

on a les relations :

x_{\sigma }={n_{\sigma } \over n_{\sigma }+n_{s}}

n_{\sigma }={m_{\sigma } \over M_{\sigma }}

n_{s}={m_{s} \over M_{s}}

ce qui conduit à :

x_{\sigma }={{m_{\sigma } \over M_{\sigma }} \over {m_{\sigma } \over M_{\sigma }}+{m_{s} \over M_{s}}}

En réécrivant on obtient, connaissant la masse molaire du solvant, la masse molaire du soluté.

La masse molaire $M_{\sigma }$ du soluté (en g/mol) est obtenue selon :

Masse molaire du soluté :

M_{\sigma }={m_{\sigma } \over m_{s}}\times {1-x_{\sigma } \over x_{\sigma }}\times M_{s}

avec $M_{s}$ la masse molaire du solvant (en g/mol).

Exemple

Le benzène a une masse molaire de 78 g/mol. À 80 °C sa pression de vapeur saturante est de 751,9 mmHg. Si l'on dissout 4,94 g de benzoate d'éthyle dans 200 g de benzène, à 80 °C la pression de vapeur saturante de celui-ci s'abaisse à 742,6 mmHg. Calculer la masse molaire du benzoate d'éthyle.

En appliquant la loi de la tonométrie, on obtient la fraction molaire du benzoate d'éthyle :

x_{\sigma }={\Delta P_{s}^{sat} \over P_{s}^{sat}}={751,9-742,6 \over 751,9}=0,01237

mol/mol

On obtient alors la masse molaire du benzoate d'éthyle :

M_{\sigma }={4,94 \over 200}\times {1-0,01237 \over 0,01237}\times 78=153,8

g/mol

Le benzoate d'éthyle a une masse molaire de 150 g/mol. La loi de la tonométrie est une bonne approche pour calculer les masses molaires, néanmoins elle reste liée à l'hypothèse de la solution idéale.

Loi de Raoult et solution idéale

Notons :

$x_{s}$ la fraction molaire du solvant ;
$x_{\sigma }$ la fraction molaire du soluté ;
$P_{s}^{\text{sat}}$ la pression de vapeur saturante du solvant pur ;
$P_{s}$ la pression de vapeur saturante abaissée du solvant.

En considérant la contrainte sur les fractions molaires : $x_{s}+x_{\sigma }=1$ , la loi de la tonométrie donne :

{P_{s}^{\text{sat}}-P_{s} \over P_{s}^{\text{sat}}}=x_{\sigma }=1-x_{s}

P_{s}^{\text{sat}}-P_{s}=P_{s}^{\text{sat}}-x_{s}\cdot P_{s}^{\text{sat}}

On obtient la loi de Raoult qui s'applique aux solutions idéales :

Loi de Raoult :

P_{s}=x_{s}\cdot P_{s}^{\text{sat}}

Dans une solution liquide idéale chacun des $N$ constituants $i$ se comporte comme un solvant, les autres constituants étant ses solutés. Chaque constituant contribue ainsi à la phase gaz par sa pression de vapeur saturante abaissée. Selon la loi de Dalton la pression totale $P$ au-dessus de la solution idéale s'écrit :

Solution idéale :

P=\sum _{i=1}^{N}P_{i}=\sum _{i=1}^{N}x_{i}P_{i}^{\text{sat}}

La pression de vapeur saturante abaissée $P_{i}$ du constituant $i$ est donc sa pression partielle.

Notes et références

Notes

Encyclopédie Universalis, « François Marie Raoult », sur Universalis.fr (consulté le 16 novembre 2020).
Académie nationale de Pharmacie, « Raoult (lois de) », sur dictionnaire.acadpharm.org (consulté le 16 novembre 2020).
Dictionnaire Larousse, « Tonométrie », sur Larousse.fr (consulté le 16 novembre 2020).

Bibliographie

Détermination des poids moléculaires : mémoires de MM. Avogadro, Ampère, Raoult, van 't Hoff, D. Berthelot, Gauthier-Villars, 1938 (lire en ligne), sur Gallica.
Mohamed Ayadim et Jean-Louis Habib Jiwan, Chimie générale, Louvain, Presses universitaires de Louvain, coll. « Cours universitaires », 2013, 376 p. (ISBN 978-2-87558-214-0, lire en ligne), p. 260-261.
Claude Friedli, Chimie générale pour ingénieur, Lausanne/Paris, PPUR presses polytechniques, 2002, 747 p. (ISBN 2-88074-428-8, lire en ligne), p. 308-310.
John C. Kotz et Paul M. Treichel Jr (trad. de l'anglais), Chimie des solutions, Bruxelles/Issy-les-Moulineaux, De Boeck Supérieur, coll. « Chimie générale », 2006, 358 p. (ISBN 978-2-8041-5232-1, lire en ligne), p. 23-26.
Claude Strazielle, Caractérisation par la détermination des masses moléculaires, vol. PE 595, Éditions techniques de l'ingénieur, 1984 (lire en ligne), p. 3-4.

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.