Histoire du calcul de la date de Pâques
Le calcul de la date de Pâques permet de déterminer le jour de Pâques et donc celui des célébrations qui s'y réfèrent (comme l'Ascension, trente-neuf jours après Pâques, et la Pentecôte, quarante-neuf jours après Pâques). La définition précise du jour de Pâques fut établie en 325 par le concile de Nicée. Les Pères du concile réunis par l'empereur Constantin la fixèrent ainsi :
« Pâques est le dimanche qui suit le 14e jour de la Lune qui atteint cet âge le 21 mars ou immédiatement après. »

Cette définition pose des problèmes redoutables de calcul astronomique et mathématique auxquels les savants s'attelèrent du IVe siècle au XXe siècle : il fallut attendre le VIe siècle pour qu'une méthode de calcul précise, élaborée, selon la tradition, par le moine byzantin Denys le Petit, soit progressivement adoptée par les Églises. Elle dut être modifiée lors de l'adoption du calendrier grégorien en 1582. Au XVIIIe siècle, les mathématiciens cherchèrent des procédés plus simples que les méthodes canoniques tout en respectant rigoureusement la définition du concile de Nicée.
Toutes les méthodes de calcul de la date de Pâques se fondent sur une Lune théorique et non sur la Lune réellement observée. De plus, les grandeurs astronomiques y sont supposées indéfiniment constantes. Or celles-ci (comme la durée du jour solaire ou celle du mois lunaire) varient sur le long terme. Les extrapolations du calcul de la date de Pâques sur plusieurs milliers d'années sont donc purement théoriques.
| Année | Occident | Orient |
|---|---|---|
| 2000 | 23 avril | 30 avril |
| 2001 | 15 avril | |
| 2002 | 31 mars | 5 mai |
| 2003 | 20 avril | 27 avril |
| 2004 | 11 avril | |
| 2005 | 27 mars | 1er mai |
| 2006 | 16 avril | 23 avril |
| 2007 | 8 avril | |
| 2008 | 23 mars | 27 avril |
| 2009 | 12 avril | 19 avril |
| 2010 | 4 avril | |
| 2011 | 24 avril | |
| 2012 | 8 avril | 15 avril |
| 2013 | 31 mars | 5 mai |
| 2014 | 20 avril | |
| 2015 | 5 avril | 12 avril |
| 2016 | 27 mars | 1er mai |
| 2017 | 16 avril | |
| 2018 | 1er avril | 8 avril |
| 2019 | 21 avril | 28 avril |
| 2020 | 12 avril | 19 avril |
| 2021 | 4 avril | 2 mai |
| 2022 | 17 avril | 24 avril |
| 2023 | 9 avril | 16 avril |
| 2024 | 31 mars | 5 mai |
| 2025 | 20 avril | |
| 2026 | 5 avril | 12 avril |
| 2027 | 28 mars | 2 mai |
| 2028 | 16 avril | |
| 2029 | 1er avril | 8 avril |
| 2030 | 21 avril | 28 avril |
| 2031 | 13 avril | |
| 2032 | 28 mars | 2 mai |
| 2033 | 17 avril | 24 avril |
| 2034 | 9 avril | |
| 2035 | 25 mars | 29 avril |
| 2036 | 13 avril | 20 avril |
| 2037 | 5 avril | |
| 2038 | 25 avril | |
| 2039 | 10 avril | 17 avril |
| 2040 | 1er avril | 6 mai |
Historique de la date de Pâques
De la Pâque juive aux Pâques chrétiennes

Pâques est la première fête célébrée dans les calendriers liturgiques chrétiens ; elle est attestée dès le IIe siècle. Elle commémore la Cène, la Passion et la Résurrection du Christ[1], événements dont les quatre évangiles situent le déroulement lors des festivités de la Pâque juive à Jérusalem, le 14 Nissan du calendrier juif.
La fête de Pâques[Note 1] était célébrée de façon diverse par les Églises chrétiennes primitives. Certaines des premières Églises continuaient à célébrer la Cène le jour de la Pâque juive, en particulier les Églises syriaques attachées à la tradition johannique qui identifiait le sacrifice du Christ à l'offrande pascale[2]. D'autres, telles l’Église de Rome, fêtaient Pâques le dimanche suivant la Pâque juive, mettant ainsi l'accent sur la Résurrection au lendemain du Shabbat[3].
Le calendrier hébreu étant lunisolaire, tous les mois commencent à la Nouvelle Lune ; le 14 du mois de Nissan correspond donc à la Pleine Lune[Note 2]. L'année du calendrier juif compte 12 ou 13 mois lunaires ; pour que Nissan reste le premier mois du printemps, l'intercalation d'un mois complémentaire était décidée par le Sanhédrin quand c'était nécessaire pour respecter le rythme des saisons[4].
Dès la fin du IIe siècle, l'évêque de Rome Victor Ier suscita plusieurs synodes en Palestine et en Syrie pour fixer à cette célébration une date commune à tous les chrétiens[5] - [6]. Le premier savant qui ait rédigé ses réflexions sur la détermination de la date de Pâques est Anatole de Laodicée (Saint Anatole), né à Alexandrie en 230, sacré évêque en 270, qui publia ses travaux dans le Canon Paschal [7] - [8] ; il utilisait deux cycles de 19 ans décalés de 3 ans. Irénée de Lyon[9] et Hippolyte de Rome[10] - [8], entre autres, suggérèrent aussi des solutions pour fixer la date de Pâques, fondées sur un cycle de 16 ans. En 314, le concile d'Arles déclara également que « la Pâque du Seigneur sera observée le même jour par tous » et demanda que la date en soit fixée par le pape Sylvestre. Cette décision ne fut guère suivie d'effets[3].
La définition du concile de Nicée
En 325, Constantin le Grand convoqua le concile de Nicée, pour mettre d'accord entre eux, sur l'orthodoxie de la foi, les trois cent dix-huit représentants du Christianisme. Ceux-ci clarifièrent la situation en s'accordant sur la définition suivante[13] - [14] :
« Pâques est le dimanche qui suit le 14e jour de la Lune qui atteint cet âge le 21 mars ou immédiatement après. »
Cette définition doit être assortie de quelques précisions : la date du est fixe et ne dépend pas de l'équinoxe de printemps, lequel peut tomber, selon les années, parfois le 19 et plus fréquemment le 20 ou le .
L'histoire est en réalité très complexe. D'une part, le cycle de Méton selon lequel il y a 19 années terrestres en 235 lunaisons jouissait encore du prestige qu'il avait acquis dans l'Antiquité pour laquelle il s'agissait d'une découverte majeure des vérités naturelles ; d'autre part les Églises d'Occident utilisaient des cycles divers dont on était bien conscient qu'il s'agissait de procédés pratiques mais sans véritable fondement naturel[Note 3]. Les Églises d'Orient, sous l'influence de la puissante Église d'Alexandrie s'étaient accordées sur le cycle de 19 ans. Les Pères du concile confièrent à l'évêque d'Alexandrie le soin de fournir une règle selon certaines prescriptions, fondées en particulier sur la date du printemps et l'aspect de la Lune. C'est donc une méthode proche de celle en vigueur alors à Alexandrie et fondée sur un cycle de 19 ans qui s'imposa. Si la définition du calcul de la date de Pâques entérinée par l'usage se fonde sur la date fixe du , c'est par souci de simplification, mais il était bien dans l'esprit du concile de prendre comme repère principal la date du printemps[Note 4]. Le quatorzième jour de la Lune signifie le treizième jour qui suit la Nouvelle Lune[Note 5] ; le terme Lune ne signifie pas ici la Lune réelle observée mais une Lune fictive, approchant assez bien la Lune réelle, appelée Lune pascale ou Lune ecclésiastique et déterminée à l'aide du cycle de Méton.
La décision des Pères, influencée par les croyances du temps, ne fut pourtant pas motivée par des raisons astronomiques, historiques ou théologiques, mais par des raisons politiques et pratiques : il fallait que Pâques ne tombe pas en même temps que la Pâque juive, non plus que les Pâques des Quartodécimains et autres mouvements hérétiques. Cela est souligné par une lettre encyclique de Constantin aux Églises[15] : « La fête de Pâques des chrétiens doit être célébrée le même jour par tous ; et pour le calcul de la date, il ne faut faire aucune référence aux Juifs. Ce serait humiliant et de plus il est possible pour eux d’avoir deux Pâques une même année. En conséquence, les Églises doivent se conformer aux pratiques suivies par Rome, l’Afrique, l’Italie, les Gaules, la Brittonie, la Libye, la Grèce, l’Asie, le Pont et la Cilicie. »
Il fut suggéré de prendre pour référence l'observation de la Lune pascale à Jérusalem[16] - [17], mais les temps de communication entre les Églises des diverses provinces de l'Empire auraient rendu impossible une célébration commune ; de plus, fixer la source de la célébration de Pâques à Jérusalem était contraire à l'esprit œcuménique de l'Église[Note 6]. Il fut donc décidé de se rapporter à une Lune théorique identique en tout lieu.
Des méthodes de calcul encore diverses
Les évêques revinrent donc du concile de Nicée avec une définition claire de la date de Pâques, mais sans méthode précise pour la calculer. Chaque Église utilisa alors sa solution particulière[18].
Pour déterminer la date de Pâques selon la définition du concile, les Alexandrins[19] se servaient du cycle de Méton (19 années terrestres font 235 mois lunaires) dans les tables de l'évêque d'Alexandrie Théophile (370-412) (tables allant de 380 à 480), puis dans celles de son neveu et successeur Cyrille (376-444) (tables allant 436 à 531). À Rome[19], après avoir utilisé au IIIe siècle une table pascale élaborée par saint Hippolyte (fondée sur un cycle de 16 ans)[20], on utilisa un cycle de 84 ans (4 cycles de Méton de 19 ans plus un cycle octaéride de 8 ans) connu sous le nom de « cycle d'Augustalis »[21] auquel on devait toutefois ajouter périodiquement un mois complémentaire lorsque l'écart entre la Lune et le Soleil atteignait 34 jours[22]. Les dates entre lesquelles la date de Pâques pouvait tomber étaient fixées pour la Lune entre les 14e et 20e jour du mois lunaire et, pour le Soleil, entre le et le [23]. Dès 280, l'alexandrin Anatole de Laodicée avait établi un cycle de 19 ans (cycle alexandrin), plus court et plus exact. La question fut résolue entre Rome et l’Orient par l’adoption du cycle oriental de 19 ans après qu’en 526, le pape Jean Ier eut chargé son primicier Boniface d’étudier le problème[22]. Convaincu de la justesse du cycle de 19 ans par Denys le Petit, moine byzantin qui vivait à Rome, le pape Boniface II promut le cycle alexandrin ; celui-ci mit longtemps à être adopté pas les Églises d'Occident[24]. On utilisa également un cycle de 95 ans (soit 5 fois 19 ans - voir ci-dessous la table pascale universelle de Périgueux)[25].
À partir de 457, Victorius d'Aquitaine fit adopter une nouvelle méthode fondée sur le « cycle de Méton » de 19 ans et sur le cycle solaire de 28 ans, créant ainsi le Computus Paschalis de (19 × 28 =) 532 ans[26]. Ce cycle fut en vigueur dans la Gaule mérovingienne à partir du concile d'Orléans de 541[3].
L'établissement du calendrier liturgique
Le calendrier liturgique se constitua progressivement à partir du IVe siècle autour de la date de célébration de Pâques. C'est tout d'abord le triduum, trois jours précédant Pâques, qui devint un temps de jeûne puis la célébration s'étendit à la semaine sainte dès 389[27]. À partir de la fin du IVe siècle, elle fut précédée des 40 jours de jeûne du carême[27]. Le temps pascal fut également étendu jusqu'à la Pentecôte, sept semaines après Pâques.
Le cycle des fêtes à dates fixes lié à Noël ne fut instauré qu'au Ve siècle, après que cette fête eut été fixée au pour remplacer la fête impériale de Sol Invictus[27].
La date de Pâques fixe encore de nos jours un grand nombre de fêtes et célébrations liturgiques qui lui sont liées par un nombre déterminé de jours, et sont par conséquent des fêtes mobiles. Les plus connues en Occident sont le Mardi Gras, le Mercredi des Cendres, la Mi-carême, le Vendredi saint et le Samedi saint, l'Ascension, la Pentecôte. En calendrier orthodoxe, les fêtes importantes sont le dimanche du Pardon, le dimanche du Jugement dernier et le lundi pur qui inaugure le grand carême.
La méthode canonique attribuée à Denys le Petit
Au milieu du VIe siècle, les diverses Églises chrétiennes adoptèrent progressivement une méthode de calcul de la date de Pâques élaborée, selon la tradition[Note 7] - [28] par le moine byzantin Denys le Petit (env. 470 - env. 540) qui travaillait à Rome dans l'entourage du pape. Cette méthode est compliquée mais exacte, car elle respecte exactement la définition du concile de Nicée. Elle prit le statut de « méthode canonique » mais mit fort longtemps à être comprise et appliquée localement.
Au VIIe siècle, en Grande-Bretagne, le sud de l'île suivait la pratique de Rome, tandis que les pays celtes — Irlandais, Gallois et Écossais — continuaient de suivre les coutumes celtiques. Oswiu de Northumbrie convoqua à l’abbaye de Whitby, en 663 et 664, un concile avec pour objet d'accorder les diverses Églises celtiques sur des problèmes de doctrine et de rite, dont le calcul de la date de Pâques. Le concile conclut, sur ce sujet, par l'adoption de la pratique de Rome, mais cette décision entra difficilement en application et il fallut la médiation de Théodore de Tarse, consacrée par le pape Vitalien, pour achever l'unification de ces Églises à partir de 669.
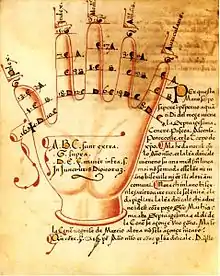
D'autres variantes locales subsistèrent longtemps, comme le montre ci-dessous la table pascale perpétuelle gravée sur le mur sud du chœur de l'église Saint-Étienne-de-la-Cité, ancienne cathédrale de Périgueux. Cette table, gravée au milieu du XIIe siècle, plus de six-cents ans après l'adoption de la méthode de Denys le Petit, ne suit pas le computus pascalis de 532 ans utilisé par celui-ci mais (avec des lacunes) un cycle de 95 ans en vigueur localement depuis huit siècles.
.JPG.webp)
Au treizième siècle, la méthode canonique était devenue en vigueur dans toutes les Églises chrétiennes à l'exception de l'Église copte et de quelques autres Églises qui suivaient leur propre calendrier (telles que les Églises chinoises, essentiellement nestoriennes au témoignage de Marco Polo[29]).
La réforme grégorienne

Par suite du décalage qui ne cessait de croître entre le calendrier et les saisons, le pape Grégoire XIII promut une réforme du calendrier qui prit effet à Rome le [30].
Ce nouveau calendrier, et le calcul de la date de Pâques qui en résultait, fut établi par les savants attachés au Pape Grégoire XIII, principalement le mathématicien allemand Christophorus Clavius[31] - [32] et l'astronome italien Luigi Giglio ou Lilius[33].
Le premier effet de la réforme, le plus spectaculaire, fut de supprimer dix jours du calendrier : ainsi, à Rome, en 1582, le lendemain du jeudi fut le vendredi .
Imposé par Grégoire XIII dans les États pontificaux, le calendrier grégorien fut aussi immédiatement adopté par l'Espagne, l'Italie, la Pologne et le Portugal. En France, Henri III l'adopta le jeudi , dont le lendemain fut le vendredi [34].
La réforme grégorienne intervient au mauvais moment : c'est l'époque des Guerres de religion où s'opposent la Réforme (globalement dans les pays du nord de l'Europe) et, dans le sud de l'Europe la Contre-Réforme, institutionnalisée par le Concile de Trente. La haine que se portent les adversaires interdit tout accord et toute concession. La Grande-Bretagne et les pays protestants n'adoptent le calendrier grégorien qu'au XVIIIe siècle, préférant, selon l'astronome Johannes Kepler, « être en désaccord avec le Soleil, plutôt qu'en accord avec le pape ». Lors de la modification du calendrier en Grande-Bretagne, le , les foules anti-papistes défilent aux cris de « nous voulons nos dix jours ! »[35]
Puisque la réforme grégorienne supprimait trois jours bissextiles tous les quatre-cents ans pour mieux approcher l'équation solaire, il fallait corriger de même l'âge de la Lune. Cette correction s'appelle la métemptose. On savait, de plus, que le cycle de Méton n'est pas absolument exact. Les astronomes promoteurs de la réforme en profitèrent pour introduire une correction du cycle, appelée proemptose[Note 8]. Ces modifications rendent le calcul de la date de Pâques grégorienne bien plus compliqué que pour la Pâques julienne[32].
Les Églises orthodoxes et le calendrier julien révisé
Les pays de tradition orthodoxe conservèrent le calendrier julien jusqu'au du début du XXe siècle. En 1918, après le révolution bolchevique, Moscou imposa le calendrier grégorien dans la nouvelle U.R.S.S.. En Grèce, dans les mois suivant le coup d'État du 11 septembre 1922, le parlement grec adopta également le calendrier grégorien. Si, pour les usages civils, les pays de culte majoritairement orthodoxe (essentiellement en Europe de l'Est et du Sud-Est) adoptèrent le calendrier grégorien avant 1927, ce ne fut pas le cas de leurs Églises nationales.
En , le congrès de Constantinople[Note 9] - [Note 10] proposa un calendrier julien révisé adoptant les règles du calendrier grégorien pour l'équation solaire et les fêtes fixes, mais fondant l'équation lunaire, et donc le calcul des fêtes mobiles — en particulier la célébration de Pâques — sur l'observation de la Lune à Jérusalem[36]. Les Églises orthodoxes refusèrent en majorité ces modifications et continuèrent de célébrer Pâques selon le calendrier julien :
Les Églises orthodoxes de Jérusalem, Russie, Macédoine, Serbie, Géorgie et Ukraine continuent d'utiliser le calendrier julien pour l'ensemble de leur calendrier liturgique. L'équation solaire du calendrier julien révisé fut acceptée par quelques Églises orthodoxes, dans l'espoir d'un meilleur dialogue avec l'Église d'Occident : le patriarcat œcuménique de Constantinople, les patriarcats d'Alexandrie et d'Antioche, les Églises orthodoxes de Grèce, Chypre, Roumanie et Pologne ainsi que celle de Bulgarie depuis 1963 [Note 11]. Elles fêtent donc Noël le selon le calendrier grégorien, ainsi que les fêtes fixes du calendrier liturgique, tandis que les fêtes mobiles, dont Pâques, restent calculées selon le calendrier julien. Cette réforme est cause des divisions au sein de ces Églises : les orthodoxes vieux-calendaristes la rejettent et s'en tiennent au calendrier julien.
Calcul canonique de la date de Pâques
Les éléments du calcul

Le calcul canonique de la date de Pâques utilise des éléments qui figurent encore fréquemment sur les calendriers, au bas du mois de février. Dans la reproduction ci-contre d'un calendrier (grégorien) de 2006, on trouve les éléments du comput :
- Épacte (0 en 2006, dans l'exemple ci-contre) ;
- Lettre dominicale (A en 2006)[Note 12] ;
- Cycle solaire (27 en 2006) ;
- Nombre d'or[Note 13] (12 en 2006) ;
- Indiction romaine (14 en 2006).
(L'Épacte, la Lettre dominicale, le Cycle solaire et le Nombre d'or présentés dans cet exemple concernent le calendrier grégorien ; ils auraient d'autres valeurs pour le calendrier julien. Quant à l'Indiction romaine, elle est indépendante du calendrier julien ou grégorien et ne sert pas au calcul de la date de Pâques[37].)
Principe du calcul canonique de la date de Pâques julienne
Le calcul canonique de la date de Pâques julienne a été établi au VIe siècle, selon la tradition, par le moine byzantin Denys le Petit. Ce calcul applique strictement la définition de la date de Pâques établie par le Concile de Nicée en 325. Le calcul canonique de la date de Pâques dépend de la périodicité à la fois de l'année solaire (année tropique) et du mois lunaire (mois synodique). Pour l'année solaire, il se fonde sur le calendrier julien qui, avec une année bissextile tous les quatre ans, pose que l'année solaire dure 365 jours un quart. Pour le mois lunaire, il se base sur le cycle de Méton selon lequel il y a presque exactement 235 mois lunaires en 19 années terrestres.
Le principe du calcul consiste à mettre en correspondance le cycle solaire (appelé aussi équation solaire), qui permet de calculer quels jours de l'année sont des dimanches, et le cycle lunaire (appelé aussi équation lunaire) qui permet, lui, de déterminer la date des Nouvelles Lunes. Pour une année donnée, l'équation solaire est spécifiée par l'un ou l'autre de deux paramètres : le Cycle solaire ou la Lettre dominicale qui sont équivalents (à une transformation près par une table ou une formule) ; l'équation lunaire est de même spécifiée par l'un ou l'autre de deux paramètres : le Nombre d'or ou l'Épacte qui sont aussi équivalents (à une transformation près par une table ou une formule).
Puisque, selon le cycle de Méton, il y a, en 19 ans, 235 Nouvelles Lunes, on peut répartir celles-ci sur un cycle de 19 années. Cela conduit à la construction d'un calendrier lunaire[38] qui donne, pour chacune des 19 années du cycle et par mois, les dates des Nouvelles Lunes[Note 14]. Pour une année donnée, connaissant sa position dans le cycle de 19 ans (son Nombre d'or), on trouve dans ce calendrier les Nouvelles Lunes de mars et d'avril, et par conséquent :
1. le quatorzième jour de la Lune qui tombe le ou immédiatement après.
D'autre part, les jours de la semaine de chaque année suivent un cycle de 28 ans (Cycle solaire ou équation solaire) qui permet de déterminer le jour de la semaine au 1er janvier de l'année (Lettre dominicale) d'où on déduit facilement les dates de l'année, en particulier celles de mars et d'avril, qui sont un dimanche. On trouve alors :
2. le premier dimanche qui tombe immédiatement après le quatorzième jour de la Lune qui tombe le ou immédiatement après.
C'est le dimanche de Pâques[Note 15].
Calcul canonique de la date de Pâques grégorienne
L'adoption, en 1582, de la réforme du calendrier julien promue par le Pape Grégoire XIII entraînait inévitablement des modifications du calcul de la date de Pâques. La suppression de trois années bissextiles tous les quatre-cents ans produisait des décalages entre le cycle solaire et le cycle lunaire qui devaient être pris en compte. De plus, les astronomes Clavius et Lilius, attachés au Pape Grégoire XIII, profitèrent de la réforme pour introduire une correction du Cycle de Méton dont on savait depuis longtemps qu'il n'était qu'une approximation. La suppression de trois jours bissextiles tous les quatre-cents ans se traduit dans le calcul de la date de Pâques par un décalage appelé métemptose. De plus, la correction du cycle de Méton conduit également à un décalage appelé proemptose.
Le calcul grégorien de la date de Pâques n'est pas une création ex nihilo mais une modification du calcul de la date de Pâques julienne. Le principe de ce calcul consiste à mettre en correspondance le cycle solaire (équation solaire), qui permet de calculer quels jours de l'année sont des dimanches, et le cycle lunaire (équation lunaire) permettant, lui, de déterminer la date des Nouvelles Lunes. Pour une année donnée, l'équation solaire est caractérisée par la Lettre dominicale qui spécifie le premier dimanche de janvier ; elle donne le moyen de calculer les jours de l'année qui sont un dimanche, en particulier en mars et avril. L'équation lunaire est caractérisée par l'Épacte, c'est-à-dire l'âge de la Lune au 1er janvier ; celle-ci permet de fixer les dates des Nouvelles Lunes de l'année, en particulier pour mars et avril. À l'aide de ces termes on détermine le dimanche qui tombe immédiatement après le quatorzième jour de la Lune qui tombe ou qui suit immédiatement le .
Les nouveautés apportées par le calendrier grégorien ont été reportées sur l'Épacte. Des règles de saut d'Épacte appliquent à l'Épacte les décalages de la date de Pâques dus à la métemptose et à la proemptose.
La date de Pâques orthodoxe
Les Églises orthodoxes fêtent Pâques selon le calendrier julien, à l'exception des Églises orthodoxes de Finlande et d'Estonie[Note 16]. Toutefois, pour des raisons pratiques, la date de Pâques orthodoxe est généralement exprimée dans le calendrier grégorien. Pour calculer la date de Pâques orthodoxe, il faut donc : calculer la date de Pâques julienne par l'un des algorithmes fournis dans les articles liés ; puis convertir la date du calendrier julien dans le calendrier grégorien[Note 17].
La correspondance des dates de Pâques dans les cultes romains et orthodoxe met en fait en jeu deux décalages, dont un seul est lié au calendrier. La date de Pâques est liée à celle de l'équinoxe de printemps, fixée au au moment où le mode de calcul a été établi ; ceci reste presque toujours vrai dans le calendrier grégorien mais est faux dans le calendrier julien du fait de la dérive séculaire. De plus, on n'utilise pas une observation de la vraie Lune, mais une Lune ecclésiastique pour déterminer Pâques. Catholiques et orthodoxes n'utilisent pas la même Lune ecclésiastique, même si les deux sont proches et toujours à moins d'une semaine d'écart. Dès lors, plusieurs décalages sont possibles :
- aucun décalage ;
- un décalage d'une semaine si un dimanche tombe entre les deux Lunes catholique et orthodoxe ;
- un décalage de quatre semaines et même cinq semaines si le des deux calendriers ne tombe pas dans la même lunaison.
Si bien que la fête de Pâques orthodoxe peut se trouver soit en même temps que la catholique (c'est le cas en 2010, 2014, 2017…), soit une semaine après (comme en 2012, 2015…), soit quatre semaines après (comme en 2021) ou même cinq semaines après (comme en 2008 ou 2013). Pâques tombe en mars ou en avril pour le culte romain (jamais en mai) ; en avril ou mai pour les orthodoxes (jamais en mars). Avec la dérive séculaire des deux calendriers, ce décalage est voué, d'ici un millénaire, à passer à quatre voire neuf semaines au lieu de zéro à cinq semaines actuellement.
Exemple
Pour 2006 :
- la date de Pâques romaine est le (en calendrier grégorien) ;
- la date de Pâques orthodoxe est le (en calendrier julien) ;
- la date de Pâques orthodoxe est le (en calendrier grégorien), soit un écart d'une semaine.
Propriétés des dates de Pâques julienne et grégorienne
La date de Pâques au plus tôt et au plus tard
Des raisonnements simples, à partir de la définition du concile de Nicée, permettent de définir les valeurs extrêmes que peut prendre la date de Pâques, au plus tôt et au plus tard en calendrier julien comme en calendrier grégorien :
Si le quatorzième jour de la Lune de mars se produit le et que ce jour est un samedi, le dimanche qui suit est le , et Pâques tombe le .
Si le quatorzième jour de la Lune de mars est le alors le prochain quatorzième jour de la Lune pascale se produit le , étant donné que le mois lunaire est réputé durer seulement 29 jours (au lieu de 30 jours) dans ce cas limite où l'épacte vaut 24. Si le est un dimanche, Pâques tombe le dimanche suivant, c'est-à-dire le .
« La date de Pâques est comprise entre le 22 mars et le 25 avril (inclus). »
Cela est valable que ces dates soient exprimées en calendrier julien ou en calendrier grégorien.
Date de Pâques orthodoxe
Le raisonnement ci-dessus s'applique au calendrier julien. Toutefois, si on transforme les dates juliennes en dates grégoriennes, on observe que :
« La date de Pâques julienne est comprise (en calendrier grégorien) entre le 4 avril et le 8 mai (inclus). »
Distribution des dates de Pâques juliennes
La date de Pâques julienne peut tomber n'importe lequel des jours de la période du au (du calendrier julien) (voir le § La date de Pâques au plus tôt et au plus tard ci-dessus). Les dates de Pâques juliennes suivent un cycle de 532 ans (soit les 19 ans du cycle de Méton combinés aux 28 ans du cycle solaire) ; c'est-à-dire que tous les 532 ans, les dates de Pâques se succèdent aux mêmes jours. Le calcul de la date de Pâques pour toutes les années d'un cycle de 532 ans permet de compter combien de fois Pâques tombe le , le …, le , le .
Le calcul (par ordinateur) du nombre de fois où la date de Pâques julienne tombe sur chacun des jours de la période - lors d'un cycle de 532 ans est résumé dans la table suivante :
| Date | Nombre d'occurrences | Date | Nombre d'occurrences |
|---|---|---|---|
| 4 | 20 | ||
| 8 | 16 | ||
| 8 | 16 | ||
| 12 | 20 | ||
| 16 | 16 | ||
| 16 | 16 | ||
| 20 | 20 | ||
| 16 | 16 | ||
| 16 | 20 | ||
| 20 | 16 | ||
| 1er avril | 16 | 16 | |
| 16 | 20 | ||
| 20 | 16 | ||
| 16 | 12 | ||
| 20 | 12 | ||
| 20 | 8 | ||
| 16 | 8 | ||
| 4 |
La distribution des dates de Pâques juliennes en calendrier julien, selon la table précédente, est représentée sur le diagramme ci-après[33] :
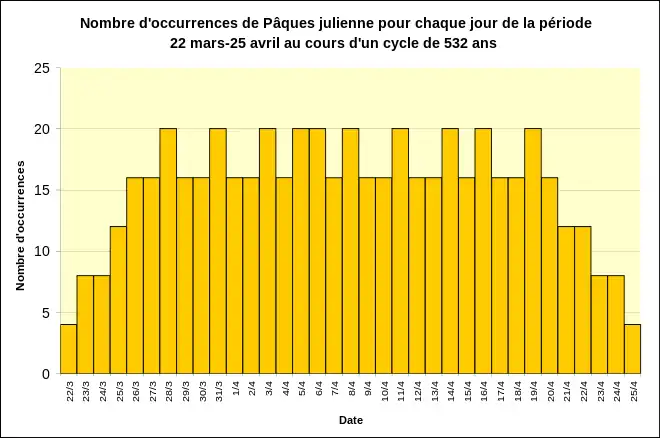
On constate que les dates extrêmes (proches du ou du juliens) sont moins susceptibles de recevoir la date de Pâques julienne. On observe aussi un pseudo-cycle de trois ans dû à la combinaison des divers cycles en œuvre.
Distribution des dates de Pâques grégoriennes
Comme pour les dates de Pâques juliennes, la date de Pâques grégorienne peut tomber n'importe lequel des jours de la période du au (du calendrier grégorien). Toutefois, le cycle des dates de Pâques grégoriennes est beaucoup plus long que celui de dates de Pâques juliennes ; en effet, la métemptose suit un cycle de 400 ans ; la proemptose suit, elle, un cycle de 25 siècles ; il faut aussi tenir compte de l'Épacte, qui a un cycle de 30 ans, et du Nombre d'or qui a un cycle de 19 ans. Finalement, les dates de Pâques grégoriennes suivent un cycle dont la période est le plus petit commun multiple de ces quatre nombres, c'est-à-dire 5 700 000 ans[Note 18].
Le calcul (par ordinateur) du nombre de fois où la date de Pâques grégorienne tombe sur chacun des jours de la période - lors d'un cycle de 5 700 000 ans est résumé dans la table suivante :
| Date | Nombre d'occurrences | Date | Nombre d'occurrences |
|---|---|---|---|
| 27550 | 192850 | ||
| 54150 | 186200 | ||
| 81225 | 192850 | ||
| 110200 | 186200 | ||
| 133000 | 192850 | ||
| 165300 | 189525 | ||
| 186200 | 189525 | ||
| 192850 | 192850 | ||
| 189525 | 186200 | ||
| 189525 | 192850 | ||
| 1er avril | 192850 | 197400 | |
| 186200 | 220400 | ||
| 192850 | 189525 | ||
| 186200 | 162450 | ||
| 192850 | 137750 | ||
| 189525 | 106400 | ||
| 189525 | 82650 | ||
| 42000 |
La distribution des dates de Pâques grégoriennes, selon la table précédente, est représentée sur le diagramme ci-après[33] :
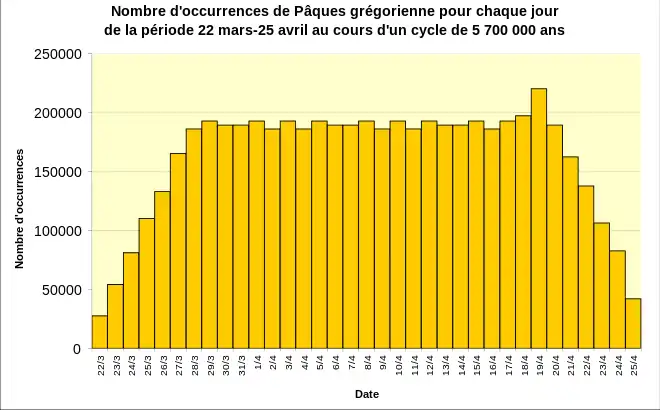
Comme pour les dates de Pâques julienne, la fréquence des dates de Pâques grégorienne est plus faible à proximité des bornes du et du . Pour le reste de la période, les occurrences sont à peu près égales, sauf pour le qui présente une fréquence plus élevée[Note 19].
Les méthodes algorithmiques de calcul de la date de Pâques
À partir du début du XVIIIe siècle, les mathématiciens recherchent des méthodes simplifiant le calcul de la date de Pâques. Le but est à la fois pratique : simplifier les calculs, et théorique : montrer que ce calcul complexe peut se réduire à une suite d'opérations arithmétiques élémentaires. Ainsi, ces mathématiciens se proposent de ramener le calcul de la date de Pâques à une suite d'opérations simples, essentiellement une série de divisions euclidiennes[39].
La première tentative de Gauss pour les Pâques grégoriennes, publiée en 1800, est une semi-réussite : tenant mal compte de la double exception sur l'Épacte (la métemptose et la proemptose), sa méthode est mise en défaut. Toutefois, Gauss, à la suite des remarques et suggestions de ses élèves et d'autres mathématiciens améliore plusieurs fois sa méthode et en publie une version quasi-définitive en 1816. Diverses améliorations ultérieures permettent finalement de publier un algorithme exact tant pour le calendrier julien que pour le calendrier grégorien. En 1814, Delambre publie un algorithme simple et exact pour le calendrier julien ; en revanche, sa solution pour le calendrier grégorien, qui fait appel à des tables et souffre d'exceptions, n'est pas satisfaisante[40]. En 1876, le journal Nature publie un algorithme, dit algorithme de Butcher, pour le calcul de la date de Pâques grégorienne, qui constitue une solution définitive et élégante du problème. La réunion de l'algorithme de Delambre pour les Pâques juliennes et celui de Butcher pour les Pâques grégoriennes est appelée algorithme de Meeus. Au cours du XXe siècle quelques autres algorithmes sont publiés pour apporter des simplifications de calcul au prix de certaines limitations quant aux périodes d'application ; depuis la diffusion des ordinateurs personnels, ces méthodes simplifiées n'ont plus grand intérêt. Dans les années 1980, John Conway publie une présentation originale du calcul de la date de Pâques grégorienne avec l'utilisation des jours-pivot.
Dans la suite, on présente de manière détaillée :
- l'algorithme de Gauss dans sa dernière version, à titre historique, parfaitement exact pour la période julienne et la période grégorienne ;
- l'algorithme de Meeus, parfaitement exact pour la période julienne et la période grégorienne ; c'est l'algorithme le plus connu et le plus utilisé ; il est très simple à programmer et peut être mis en œuvre avec un simple tableur ;
- l'algorithme de Conway, applicable seulement aux dates de Pâques grégoriennes mais qui utilise une méthode de calcul originale.
On cite ensuite, avec références, divers algorithmes publié de la fin du XIXe siècle jusqu'aux années 1960, dont plusieurs présentent des limitations.
L'algorithme de Gauss
La méthode de Gauss présente un grand intérêt historique car c'est la première tentative d'élaboration d'une méthode algorithmique de calcul de la date de Pâques. L'ambition de Gauss était de créer un algorithme unique qui serait universellement valable pour les Pâques juliennes comme pour les Pâques grégoriennes. En 1800[41], il publie la première méthode de calcul de la date de Pâques essentiellement fondé sur des opérations arithmétiques élémentaires. Toutefois, sa méthode tient mal compte des sauts d'Épacte pour la métemptose et la proemptose. À la suite de diverses corrections proposées par ses correspondants mathématiciens et ses élèves, il publie une version presque exacte en 1816[42]. La version publiée dans l'article détaillé, après diverses corrections, est valide pour toutes les années en calendrier julien et en calendrier grégorien. On pourra noter que le calcul pour les dates de Pâques juliennes est très voisin de l'algorithme de Delambre.
Gauss, prudent, et qui ne disposait pas des moyens actuels de calcul, limitait la validité de sa méthode à la période 1700-4099. Toutefois, des vérifications systématiques par ordinateur montrent que cet algorithme est universellement valide pour toute date à partir de 326 pour les Pâques juliennes et pour toute date à partir de 1583 pour les Pâques grégoriennes[Note 20].
L'algorithme de Meeus
L'histoire de cet algorithme est curieuse : en 1876, un « correspondant de New York » inconnu envoie au journal britannique Nature[43] un algorithme de la date de Pâques grégorienne pour une année quelconque. En 1877, Samuel Butcher, évêque de Meath, montre dans The ecclesiastical calendar[44] que cette méthode est exacte[Note 21] sans limite de date. L'algorithme est ensuite reproduit en 1922 par H. Spencer Jones dans son Astronomie générale[45], en 1977 par Old Farmer's Almanac, en 1988 par Peter Duffett-Smith, de l'Université de Cambridge[46] dans Practical Astronomy with your Calculator[47] et, en 1991, par Jean Meeus dans ses Algorithmes astronomiques[48].
Cette méthode est appelée « algorithme de Butcher ». La réunion de cet algorithme avec la méthode de Delambre constitue l'algorithme de Delambre-Butcher. Il est plus souvent connu sous le nom d'algorithme de Meeus, le livre de celui-ci[49] en ayant assuré la diffusion mondiale.
L'algorithme de Meeus a l'avantage de ne présenter aucune limitation de date ni pour les Pâques juliennes ni pour les Pâques grégoriennes[Note 22]. Cette méthode n'exige aucune instruction conditionnelle ni le recours à aucune table. Sa mise en forme est extrêmement simple et un simple tableur, sans aucune programmation, suffit. Mathématiquement, c'est la méthode la plus élégante. C'est aussi la plus connue et la plus utilisée des méthodes de calcul de la date de Pâques.
L'algorithme de Conway
L'intérêt principal de l'algorithme de Conway est d'introduire une présentation nouvelle du calcul de la date de Pâques grégorienne à l'aide du concept de Jour-pivot.
Il existe chaque année une série de dates mensuelles qui tombent toujours le même jour de la semaine. Cette série de dates est constante pour les dix derniers mois de l'année et varie pour janvier et février selon que l'année est ou non bissextile. Pour les années normales, cette série de dates est : (31/01, 28/02, 7/03, 4/04, 9/05, 6/06, 11/07, 8/08, 5/09, 10/10, 7/11, 12/12) et pour les années bissextiles, le 31/01 devient le 1/02 et le 28/02 devient le 29/02. On pourra vérifier sur le calendrier de 2006, année non bissextile, reproduit en tête de cet article, que le jour-pivot pour 2006 est un mardi. De plus les jours-pivot séculaires suivent un cycle de 400 ans. Conway utilise ces propriétés pour déterminer la Lune pascale et le dimanche de Pâques.
Les contrôles effectués par ordinateur prouvent que la méthode, dans la présentation qui en est donnée dans l'article détaillé, est exacte et donne les mêmes résultats que l'algorithme de Meeus pour un cycle de 5 700 000 ans à partir de 1583.
Autres méthodes algorithmiques du calcul de la date de Pâques
La recherche de méthodes simplifiées de calcul de la date de Pâques avait un grand intérêt à l'époque du calcul manuel : unifier les calculs, éviter le recours à des tables, gagner sur chaque opération arithmétique épargnait alors labeur, temps et risque d'erreur. Depuis l'apparition du calcul mécanique, la recherche de simplification est moins cruciale : écrire une ligne de programme en plus ou en moins n'est guère coûteux ; de plus, les temps de calcul, même pour des algorithmes peu optimisés, sont raisonnables[Note 23].
Des mathématiciens se sont attachés à mettre sous forme d'algorithmes programmables les méthodes canoniques de Denys le Petit pour le calendrier julien ou de Lilius-Clavius pour le calendrier grégorien (trois algorithmes de Henk Reints) ; d'autres ont proposé des méthodes simplifiées mais susceptibles de certaines restrictions (comme les algorithmes de Carter[50] ou de Thomas O'Beirne[51]).
Voici plusieurs de ces méthodes dans l'ordre chronologique de leur publication :
| Auteur | Note | Validité, référence |
|---|---|---|
| Christian Zeller | Astronome allemand (1822-1899) qui travailla et publia également en France. Il œuvra beaucoup sur les problèmes calendaires et la date de Pâques. On trouvera des références bibliographiques dans sa notice ainsi, que dans la bibliographie ci-après, plus particulièrement sur la date de Pâques. | Sa méthode pour le calendrier julien est aussi simple que celle de Delambre. En revanche, sa méthode pour le calendrier grégorien n'est pas universellement valable en l'état : l'algorithme original est limité à l'année 4200[52]. |
| Carter | La seule référence connue à l'algorithme de Carter est une note de travail du Royal Greenwich Observatory[53]. Cet algorithme daterait des années 1920 - 1930. | La méthode de Carter détermine la date de Pâques grégorienne dans le calendrier grégorien. Toutefois, cette méthode est limitée à la période 1900 - 2099[54]. |
| J.M.Oudin, Claus Tøndering | Dans les années 1930, J.-M. Oudin, pseudonyme de Frère Namase-Marie, décèle précisément les insuffisances de l'algorithme de Gauss concernant la proemptose. Ses corrections paraissent successivement en 1939[55] et, en 1940, dans le Bulletin astronomique[56]. Claus Tøndering est un ingénieur informaticien danois né en 1953 qui a repris, amélioré et diffusé l'algorithme de Oudin[57]. | Cet algorithme calcule la date de Pâques julienne en calendrier julien et la date de Pâques grégorienne en calendrier grégorien[58]. |
| Denys le Petit, Henk Reints | Le mathématicien néerlandais Henk Reints a mis sous forme algorithmique la méthode canonique de Denys le Petit pour la date de Pâques julienne. | Cet algorithme calcule la date de Pâques julienne en calendrier julien[59]. |
| Lilius-Clavius, Henk Reints | Le mathématicien néerlandais Henk Reints a aussi mis sous forme algorithmique la méthode canonique de Lilius-Clavius pour Pâques en date grégorienne. Cet algorithme calcule la date de Pâques grégorienne en calendrier grégorien. | L'algorithme détaillé est disponible sur le site en référence[59]. |
| Henk Reints | Cet algorithme grégorien est une simplification de l'algorithme de Lilius/Clavius présenté ci-dessus. Il a été développé par le mathématicien néerlandais Henk Reints. | Cet algorithme calcule la date de Pâques grégorienne en calendrier grégorien[60]. |
| Thomas O'Beirne | Thomas H. O'Beirne, de Glasgow, a publié son algorithme en 1965. | Cet algorithme est explicitement limité par son auteur aux années 1900-2099. Une seconde publication, légèrement modifiée, en 1966, n'indique pas de limitation. Dans le doute, on doit considérer que cet algorithme est limité aux années 1900-2099. Cet algorithme est disponible sur le site en référence[61]. |
| Louis-Aimé de Fouquières | Dans son ouvrage L’Heure milésienne[62], l’auteur propose une méthode dérivée de celles de Meeus et de John Conway, avec une variante originale pour le calcul de la correction des épactes 24 et 25 de la méthode canonique. Le texte introduit les concepts de reliquat pascal, écart pascal et quantième pascal pour aider à suivre la démarche de calcul. La méthode commence par une décomposition de l’année cible, plus intuitive que la suite de divisions entières présentée dans les autres algorithmes. Ainsi présentée, la méthode tient en cinq lignes de calcul. | La méthode donne le même résultat que la méthode de Meeus pour les 5 700 000 années postérieures à 1582. Le site web du calendrier milésien explique la méthode et propose un calculateur annuel ainsi qu’un lien vers le programme de comparaison entre la méthode de Meeus et la méthode milésienne[63]. |
Calcul de la date de Pâques au quotidien
L'algorithme de calcul de la date de Pâques (selon la méthode de Meeus) est inclus dans plusieurs tableurs et est disponible avec la fonction DIMANCHEDEPAQUES() dans LibreOffice Calc.
Notes et références
Notes
- La fête de Pâques chrétienne est normalement orthographiée avec un s et se distingue de la Pâque juive écrite au singulier. La locution date de Pâques est une ellipse pour date du jour de la fête de Pâques.
- C'est-à-dire le quatorzième jour de la Lune. Voir ci-après les détails sur la définition du Concile de Nicée.
- Rappelons que jusqu'au XVIe siècle on a pensé que les astres, situés dans l'orbe des parfaits étaient organisé selon une géométrie ordonnée et suivaient des règles géométriques complexes mais accessibles à l'entendement ; voir par exemple les constructions polyédriques de Kepler sur l'agencement des astres. Voir Kepler et l'agencement polyédrique des astres.
- Voir l'article Calendrier julien révisé#Équation lunaire
- Pour calculer les intervalles de temps, les Anciens incluaient dans le décompte le jour de début et le jour de fin. Ainsi, d'un dimanche au suivant, ils comptaient huit jours, et non pas sept selon notre méthode moderne de décompte (c'est la raison pour laquelle, dans le langage courant, on dit « dimanche en huit », et non pas « dimanche en sept », pour désigner le dimanche qui suit le dimanche prochain.) Aussi, pour déterminer le quatorzième jour de la Lune, il faut ajouter 13 à la date de la Nouvelle Lune : par exemple si la Nouvelle Lune est le 9 janvier, le quatorzième jour de la Lune est le 22 janvier.
- Ce sont les mêmes raison qui conduisirent le Conseil français du culte musulman à proposer, en 2012, une Lune de Ramadan universelle, fondée sur le calcul astronomique. Voir Détermination du Ramadan par le CFCM. Cette proposition fut suivie en 2013 de façon très inégale.
- S'il est presque certain que c'est Denys le Petit qui a défini l'Ère de l'Incarnation comme débutant le 25 décembre 753 AUC, reportée par commodité au 1er janvier 754 AUC, son rôle dans le calcul de la date de Pâques relève de la tradition, les sources sur ce sujet étant sujettes à caution.
- À l'époque de la réforme grégorienne, la dérive du cycle de Méton sur la Lune vraie était connue depuis longtemps. À l'aide des relevés astronomiques dont ils disposaient, parfois très anciens (datant des babyloniens), Clavius et Lilius estimèrent cette dérive à un jour tous les 312,5 ans. Toutefois, soit que les relevés qu'ils utilisèrent aient été entachés d'erreurs, soit que cette dérive ait changé dans le temps, leurs calculs paraissent de nos jours très sous-estimés. Avec une année terrestre tropique, évaluée aujourd'hui à 365,242 181 jours, et un mois lunaire synodique de 29,530 589 jours, un calcul simple conduit à une dérive du cycle de Méton sur la Lune vraie d'un jour tous les 218,9 ans. La proemptose est donc sous évaluée et il demeure dans le calcul grégorien de la date de Pâques, malgré cette correction, une dérive de la Lune vraie sur la Lune théorique d'environ un jour tous les 1043 ans.
- Cette réunion est aussi nommée Synode de Constantinople (de 1923) ou Synode d'Istanbul (de 1923). Le terme « synode » définit une réunion plus formelle qu'un « congrès ». Les références à Istanbul sont anachroniques. À la suite de la révolution d'Ataturk, il ne fut recommandé d'appeler la ville Istanbul qu'en 1928 et ce nom ne devint d'usage officiel que le 28 mars 1930. Voir Noms d'Istanbul.
- Le terme « panorthodoxe » est tendancieux : ce qualificatif fut imposé par les partisans du congrès, alors qu'une très petite minorité des Églises orthodoxes y participaient ; voir à ce sujet l'article Calendrier julien révisé.
- Certaines paroisses occidentales de l'Église orthodoxe russe célèbrent également la Nativité le 25 décembre grégorien, ainsi que celles des diocèses orthodoxes bulgares d'Amérique, avant et après le transfert en 1976 de ce diocèse de l'Église orthodoxe russe hors frontières à l'Église orthodoxe en Amérique.
- Attention. Il existe entre les lettres dominicales et leur correspondance numérique plusieurs conventions qui peuvent rendre la lecture des algorithmes incompréhensible si la convention adoptée par l'auteur n'est pas nettement précisée. Par exemple, certains posent : A=0, B=1,…, G=6 ; d'autres prennent A=1, B=2,…, G=7 ; d'autres comptent en sens rétrograde : G=0, F=1,…, G=6, etc. Dans cet article et les articles liés, la convention est : A=1, B=2,…, G=7.
- Aucun rapport avec la proportion géométrique de même nom.
- Cette répartition comporte un certain arbitraire. Le calendrier lunaire établi par Denys le Petit doit être considéré comme une hypothèse qui fonde les calculs ultérieurs
- Pour l'ensemble de ces calculs, voir l'ouvrage de Jean Lefort, La saga des calendriers, cité en référence.
- Voir Pâques#Célébrations religieuses.
- On pourra à cet effet utiliser les algorithmes donnés dans l'article Jour julien : convertir la date du calendrier julien en Jours juliens puis convertir les Jours juliens en date du calendrier grégorien.
- Ce cycle est purement théorique. Sur le long terme, tout bouge : la rotation de la Terre ralentit, donc la durée du jour s'allonge (de 1 à 2 ms par siècle) et la durée du jour lunaire varie en conséquence ; les divers cycles sur lesquels s'appuie le calcul de la date de Pâques sont variables à long terme. Or ce calcul suppose ces cycles constants. Le calcul de la date de Pâques sur d'aussi longues périodes est donc fictif.
- L’histogramme des dates de Pâques sur un cycle de 5 700 000 années a une forme de trapèze.
Les fréquences de la date de Pâques, plus faibles en début et en fin de période, sont dues à la combinaison des valeurs de l'Épacte avec celles de la lettre dominicale : Pâques au nécessite que l'Épacte vaille 23 et la lettre dominicale D, soit une seule possibilité ; le est obtenu avec deux possibilités : Épacte = 22 ou 23 et lettre dominicale E, etc. Il en résulte l'aspect quasi linéaire de l'accroissement des fréquences (quasi car les lettres dominicales ne sont pas équiprobables).
On atteint ensuite un plateau. Les irrégularités sont dues aux variations de fréquence de la lettre dominicale.
Pour le , la fréquence des dates de Pâques est un peu supérieur à celle obtenue pour le 4 et le : c’est l’effet direct de la correction de l'Épacte XXV pour la lettre dominicale C qui avance au les dates de Pâques qui seraient tombées le sans cette correction.
La fréquence élevée pour le résulte du traitement particulier des Épactes 24 et 25. L'Épacte 24 est assimilé à 25 pour le calcul de la date de Pâques, ce qui augmente d’un facteur 1,94 la probabilité de la Pleine Lune le par rapport à une Épacte normale ; ceci accroît en conséquence la fréquence des dates de Pâques liées à cette Pleine Lune, du 19 au .
Ce phénomène se produit aussi pour les jours suivant le : on peut constater que le trapèze est dissymétrique, les occurrences dans les derniers jours sont plus nombreuses que dans les premiers. Les sept derniers jours de la période, du 19 au , reçoivent plus fréquemment Pâques que les sept premiers, mais l’effet est surtout apparent pour le .
Micher Dorrer, Notes sur la date de Pâques, École polytechnique, 2012. - Vérification effectuée à l'aide de l'algorithme de Meeus.
- C'est-à-dire respectant exactement la définition du concile de Nicée.
- Logiquement, la date de Pâques julienne n'a pas de sens avant sa définition par le Concile de Nicée en 325, et la date de Pâques grégorienne n'a pas de sens avant 1583, le calendrier grégorien ayant pris effet le 15 octobre 1582.
- À titre d'exemple, le calcul du nombre d'occurrences de la date de Pâques grégorienne pour 5 700 000 ans (voir le § Distribution des dates de Pâques grégoriennes ci-dessus) par la méthode de Butcher prend, avec un PC ordinaire moyennement performant et d'une macro Excel peu rapide moins de 5 minutes (calcul effectué en janvier 2013).
Références
- Michel Rouche, Les origines du christianisme 30-451, Hachette, p. 48
- Pâque juive et Pâques chrétienne : un même calendrier ? Article de Jean-Paul Michaud sur le site Interbible
- Pierre Maraval, Le christianisme de Constantin à la conquête arabe, p. 236-238
- La Bible indique que Pessah doit avoir lieu quand l'orge est bon à couper. Aussi le mois précédent Nissan, Adar, était redoublé en Veadar en fonction du murissement des épis. Cf Jean Lefort, La saga des calendriers, Bibliothèque pour la science, , p. 93
- Michel Rouche, Les origines du christianisme 30-451, Hachette, p. 63
- Yves Chiron, Histoire des conciles, Perrin, , p. 9
- Jean-Paul Parisot, Françoise Suagher, Calendriers et chronologie, Paris, Masson, 1996 ; (ISBN 2-225-85225-1), p. 95.
- Voir L'art de vérifier les dates des faits historiques, des chartes, des chroniques et autres anciens monuments, depuis la naissance de Notre-Seigneur, Volume 1, par Maur-François Dantine, Charles Clémencet (dom), François Clément (dom), M. de Saint-Allais (Nicolas Viton), Ursin Durant, Valade, imprimeur du roi, rue Coquillière, 1818, fac-simile sur Google Books ici
- Irénée de Lyon, Démonstration de la prédication apostolique, Introduction, traduction et notes par Adelin Rousseau, moine de l'abbaye d'Orval, Éditions du Cerf, Paris, 1995, (2e éd. 2011), 420 p., (ISBN 2-204-05110-1)
- Élève d'Irénée de Lyon aurait eu le premier, selon la tradition, l'idée de dresser des tables permettant de trouver facilement la date de Pâques Consulté le 26/10/2013
- Texte liturgique grec
- Différences entre les textes de 325 et 381
- J. Lévy, Détermination de la date de Pâques, Paris, Annuaire du Bureau des longitudes, Lire ici.
- Actes du Concile de Nicée. Lire ici
- Voir ce site.
- Voir le site Les dates de Pâques
- Voir Calendrier julien révisé
- Observatoire de Paris, Le calcul des dates de Pâques. Lire ici.
- P. Rocher, Institut de mécanique céleste et de calcul des éphémérides, Observatoire de Paris. Voir : ce texte
- Voir La vie des saints et des festes de l'année Fac-simile Google, page 61
- Voir sur le cycle d'Augustalis
- Georges Briche, Rapports entre les colombaniens et les autorités ecclésiales, voir le fac-simile de l'ouvrage ici
- A. Cordiolani, Les computistes insulaires et les écrits pseudo-alexandrins, article, Bibliothèque de l'école des chartes, volume 106, no 1, pp. 5-34, fac-simile sur Persée ici
- Georges Briche Rapport entre colombaniens et autorités ecclésiales
- On trouvera des études détaillées de cette table sur les sites suivants : Étude classique d'Alfred Cordiolani (1961) et Easter dates in an inscription at Périgueux (en anglais)
- La vie des saints et l'histoire des festes de l'année, avec privilège du Roy ; à Paris, chez la Veuve Roulland, rue Saint-Jacques vis-à-vis Saint Yves ; MDCCXXIV ; page 29. Fac-simile sur Google Books
- Michel Rouche, Les origines du christianisme 30-451, Hachette, p. 149
- Voir ici une recension des sources primaires prétendues de la réforme de Denys le Petit.
- Le Devisement du monde ou Le livre des merveilles, rédigé en franco-provençal et disponible dans de nombreuses éditions francisées.
- Voir l'article Calendrier grégorien.
- Romani Calendarii ad Gregorio XIII, PM, Restituti explicatio, Rome, 1603.
- Voir le fac simile avec traduction en anglais de l'ouvrage de Clavius explicitant les calculs de la date de Pâques sur le site de l'University of Notre Dame, South Bend (Indiana), États-Unis.
- Jean Lefort, La saga des calendriers ; Paris, Éd. Bibliothèque Pour la Science, 1998, (ISBN 9782902900350).
- Jean Lefort, La Saga des Calendriers, p. 74
- La réforme grégorienne en Grande-Bretagne
- Une Pâques commune Article paru en 2011 sur le site Chrétiens de la Méditerranée
- Voir l'article Comput.
- Jean Lefort, La saga des calendriers : ou le frisson millénariste, Paris, Belin (http://www.editions-belin.com/ Site des Éditions Belin), coll. « Pour la Science », , 192 p. (ISBN 978-2-84245-003-8). On peut également consulter Vénance Grumel Traité d'Etudes byzantines -Tome I La Chronologie P.U.F. 1958, Chapitre III Le cycle lunaire pascal de 19 ans pages 31 à 55.
- Voir l'article Division euclidienne.
- Jean-Baptiste, Joseph Delambre, Astronomie théorique et pratique ; Paris, Vve Courcier, 1814 ; vol. 3, p. 715. Fac-simile de l'Astronomie théorique et pratique sur (https://books.google.fr/books/about/Astronomie_th%C3%A9orique_et_pratique.html?hl=fr&id=BDAVAAAAQAAJ Google Books].
- Voir l'original du texte de Gauss en allemand.
- Voir : « la version révisée de 1816 en allemand. »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?)
- Nature, 1876 April 20, vol. 13, p. 487.
- Samuel Butcher, The Ecclesiastical Calendar ; Its theory and construction ; Dublin, Hodges, Foster and Figgis, 1877, p. 225. Fac-simile sur Google Books. (livre posthume publié par ses fils)
- H. Spencer Jones, General Astronomy ; London, Longsman, Green, 1922 ; p. 73. Fac-simile sur Google Books.
- Voir sa page personnelle ici
- Peter Duffet-Smith Practical Astronomy with your Calculator, Cambridge University Press, 2 février 1989, 3e édition, 200 pages, (ISBN 978-0521356992)
- Jean Meeus, Astronomical Algorithms ; Richmond (Virginia, États-Unis), Willmann-Bell, 1991, pp. 67–68.
- Jean Meeus, op. cit.
- Voir : Algorithme de Carter.
- Voir Algorithme de O'Beirne.
- L'algorithme de Zeller détaillé est disponible sur ce site.
- Voir ce site.
- L'algorithme de Carter détaillé est disponible sur ce site.
- J.M. Oudin, Annales de la Société Scientifique de Bruxelles, Série I, 59 ; Bruxelles, 1939, pp. 225-226 ; Nouvelles formules, très simples, très rapides, en fonction, du seul millésime & Tables pour calculer la date de Pâques par ces formules.
- Bulletin astronomique ; mémoires et variétés, Volume 12-8 ; Paris, Gauthier-Villars, 1940, Étude sur la date de Pâques, pp. 391-410.
- Le site de Claus Tøndering concernant le calendrier est visible ici.
- Voir Calcul de la date de Pâques selon l'algorithme de Oudin-Tøndering ce site
- Voir ce site.
- Voir le site de Henk Reints (en néerlandais), .
- Voir ce site.
- Louis-Aimé de Fouquières, L'Heure milésienne. Mieux connaître le temps de la Terre avec le calendrier milésien., Paris, Edilivre, , 142 p. (ISBN 978-2-334-23604-1), p. 62-70
- « Calcul date de Pâques », sur www.calendriermilesien.org, (consulté le )
Voir aussi
Ouvrages généraux
- Jean-Paul Parisot et Françoise Suagher, Calendriers et chronologie, Paris, Masson, , 209 p. (ISBN 2-225-85225-1).
- Jean Lefort, La saga des calendriers, Paris, Éd. Bibliothèque Pour la Science, 1998, ( (ISBN 978-2-8424-5003-8)).
- Venance Grumel, Traité d'études byzantines - Tome Ier La Chronologie P.U.F., 1958.
- Harold Spencer Jones, General Astronomy, London, Edward Arnold and Company, 1924 ; ( (ISBN 0217219276)).
- Jean-Baptiste Joseph Delambre, Astronomie théorique et pratique, Paris, Vve Courcier, 1814. Fac-simile de l'Astronomie théorique et pratique sur Google Books.
- Dominique Ladiray, Benoît Quenneville, Désaisonnaliser avec la méthode X-11, Bureau du recensement des États-Unis—Chapitre 5 Modélisation de l'effet de Pâques.
Méthodes canoniques
- Denys le Petit, Liber de Paschate. Texte en latin. ;
- Christophorus Clavius, Opera mathematica (le cinquième volume contient une explication détaillée du calcul de la date de Pâques grégorienne) ; fac-simile de l'original en latin et traduction en anglais sur le site de University of Notre Dame [archive], South Bend (Indiana), États-Unis ici.
- Christophorus Clavius, Romani Calendarii ad Gregorio XIII, PM, Restituti explicatio, Rome, 1603.
Algorithme de Meeus
- Samuel Butcher, The Ecclesiastical Calendar ; Its theory and construction, Dublin, Hodges, Foster and Figgis, 1877, p. 225. Fac-simile sur Google Books.
- Jean Meeus, Astronomical algorithms, Richmond, Virginia, Willmann-Bell, 1991 (ISBN 0943396352).
Algorithme de Gauss
- Fac-simile de l'original du texte de Gauss sur ce site.
Algorithme de Conway
- John Horton Conway, Calendar Calculations (règle du Jour-pivot), Mathematical Surprises, janvier/, p. 46 ;
- John Horton Conway, Elwyn R. Berlekamp & Richard K. Guy, Winning Ways for your Mathematical Plays, Volume II, Games in Particular, pp. 795-800 ; New York Academic Press, 1982 ; (ISBN 0-12-091152-3) ;
- Sidney West Graham, The Doomsday Rule (La règle du jour-pivot), Université de Central Michigan, . À lire en anglais sur ce site.
Algorithme de Zeller
- Christian Zeller, Die Grundaufgaben der Kalenderrechnung auf neue und vereinfachte Weise gelöst, Württembergische Vierteljahrshefte für Landesgeschichte, Jahrgang V (1882), pp. 313-314.
- Christian Zeller, Problema duplex Calendarii fundamentale, Bulletin de la Société Mathématique de France, vol.11, (Séance du ), pp. 59-61.
- Christian Zeller, Kalender-Formeln ; Mathematisch-naturwissenschaftliche Mitteilungen des mathematisch-naturwissenschaftlichen Vereins in Württemberg, ser. 1, 1 (1885), pp. 54-58.
- Christian Zeller, Kalender-Formeln ; Acta Mathematica, vol.9 (1886-7), , pp. 131-136.
Algorithme de O'Beirne
- Thomas Hay O'Beirne, The regularity of Easter, Bulletin of the Institute of Mathematics and its Applications, 1966, vol 2, numéro 2, pp. 46-49.
- Thomas Hay O'Beirne, Puzzles and Paradoxes, New York, Oxford University Press, 1965, 238 p., dernière édition : 27/02/2002.
Articles connexes
- Pâques
- Pessa'h (Pâque juive)
- Comput ecclésiastique
- Calendrier liturgique romain
- Fêtes mobiles dans le rite romain
- Fêtes mobiles dans le rite byzantin
- Calcul canonique de la date de Pâques julienne
- Calcul canonique de la date de Pâques grégorienne
- Calcul de la date de Pâques selon la méthode de Gauss
- Calcul de la date de Pâques selon la méthode de Meeus
- Calcul de la date de Pâques selon la méthode de Conway
- Dates de passage du calendrier julien au calendrier grégorien par pays
- Modèle:Dates de Pâques
Liens externes
- Années classées par date de Pâques ;
- Comparaison de différents algorithmes (très documenté) ;
- Plusieurs algorithmes avec explications (et ponctuellement quelques fautes de frappe dans les formules, dommage) ;
- Sur le site de l’IMCCE :
- Tableau de Pâques de Dionysius Exiguus.
- Sur le site de la grande histoire du calendrier :