Sous-différentiel

En mathématiques, et plus précisément en analyse convexe, le sous-différentiel est un concept permettant de décrire la variation locale d'une fonction convexe (à valeurs réelles donc) non nécessairement différentiable dans un sens classique, celui auquel on attache aujourd'hui le nom de Fréchet. Au lieu d'être la pente de l'application linéaire tangente (c'est-à-dire, la dérivée) au point considéré, qui n'existe pas nécessairement, le sous-différentiel d'une fonction convexe est l'ensemble des pentes de toutes les minorantes affines de la fonction, qui sont exactes en ce point, c'est-à-dire qui ont en ce point la même valeur que la fonction convexe qu'elles minorent. Dans cette description, le mot pente peut être entendu comme un élément de l'espace dual. La convexité de la fonction assure qu'on peut lui trouver des minorantes affines exactes en presque tout point de son domaine ; on met donc à profit cette propriété pour définir le sous-différentiel. Si l'on peut trouver une minorante affine exacte en un point donné, on dit que la fonction convexe est sous-différentiable en ce point.

On sait que la notion de dérivée est fondamentale en analyse car elle permet d'approcher localement des fonctions par des modèles linéaires, plus simples à étudier. Ces modèles fournissent des renseignements sur les fonctions qu'ils approchent, si bien que de nombreuses questions d'analyse passent par l'étude des fonctions linéarisées (stabilité, inversibilité locale, etc). On rencontre beaucoup de fonctions convexes qui ne sont pas différentiables au sens classique, en particulier lorsque celles-ci résultent de constructions qui n'ont rien pour assurer la différentiabilité des fonctions qu'elles produisent. Il en est ainsi de la fonction duale associée à un problème d'optimisation sous contraintes, pour en citer un exemple emblématique. Pour ces fonctions convexes non lisses, le sous-différentiel joue donc un rôle similaire à celui de la dérivée des fonctions plus régulières.

La notion de sous-différentiel connaît diverses extensions aux fonctions non nécessairement convexes, par exemple aux fonctions localement lipschitziennes[1].

Connaissances supposées : l'algèbre linéaire, le calcul différentiel (notamment les propriétés de la dérivée directionnelle au sens de Dini pour les fonctions convexes prenant des valeurs infinies), les bases de l'analyse convexe (notamment les principales notions attachées aux ensembles et aux fonctions convexes, mais surtout la notion de fonction conjuguée).

Fonction d'une seule variable

Définition

Une fonction convexe non différentiable (en bleu) et deux de ses minorantes affines exactes en

x_{0}

(rouge). Le sous-différentiel de cette fonction en

x_{0}

est l'ensemble des pentes de ces minorantes affines exactes en

x_{0}

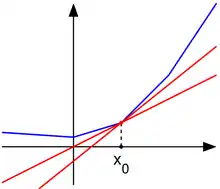
De manière rigoureuse, une sous-dérivée d'une fonction convexe $f:I\to \mathbb {R}$ en un point $x_{0}$ de l'intervalle ouvert $I$ est un nombre réel $s$ tel que

$f(x)\geqslant f(x_{0})+s(x-x_{0}),$

pour tout $x$ dans $I$ . On peut montrer que si $x_{0}$ est dans l'intérieur de $I$ , l'ensemble des sous-dérivées en $x_{0}$ est un intervalle fermé non vide, donc de la forme $[a,b]$ , avec des bornes $a$ et $b$ données par

${\begin{array}{rcl}a&=&\displaystyle \lim _{x\uparrow x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}},\\b&=&\displaystyle \lim _{x\downarrow x_{0}}{\frac {f(x)-f(x_{0})}{x-x_{0}}},\end{array}}$

qui sont finies et qui vérifient $a\leqslant b$ .

L'ensemble $[a,b]$ de toutes les sous-dérivées est appelé le sous-différentiel de la fonction $f$ en $x_{0}$ .

Exemples

Considérons la fonction f(x)=|x| qui est convexe. Alors, le sous-différentiel à l'origine est l'intervalle [−1, 1]. Le sous-différentiel en n'importe quel point x₀<0 est le singleton {−1} et le sous-différentiel en n'importe quel point x₀>0 est le singleton {1}.

Propriétés

Une fonction convexe f:I→R est différentiable en x₀ si et seulement si le sous-différentiel ne contient qu'un seul point, qui est alors la dérivée de f en x₀.

Un point x₀ est un minimum local de f si et seulement si zéro est contenu dans le sous-différentiel, c'est-à-dire, dans la figure ci-dessus, on peut tracer une droite horizontale "sous-tangente" au graphe de f en (x₀, f(x₀)). La dernière propriété est une généralisation du fait que la dérivée d'une fonction dérivable en un minimum local est nulle.

Fonction définie sur un espace euclidien

On suppose dans cette section que $\mathbb {E}$ est un espace euclidien (de dimension finie donc) dont le produit scalaire est noté $\langle \cdot ,\cdot \rangle$ et la norme associée $\|\cdot \|$ . On note par ailleurs

${\bar {\mathbb {R} }}:=\mathbb {R} \cup \{-\infty ,+\infty \}$ la droite réelle achevée,
$\operatorname {dom} \,f:=\{x\in \mathbb {E} :f(x)<+\infty \}$ le domaine d'une fonction $f:\mathbb {E} \to {\bar {\mathbb {R} }}$ , qui peut donc prendre la valeur $-\infty$ sur son domaine,
$\operatorname {Conv} (\mathbb {E} )$ l'ensemble des fonctions $f:\mathbb {E} \to {\bar {\mathbb {R} }}$ qui sont convexes (c'est-à-dire, leur épigraphe est convexe) et propres (c'est-à-dire, elles ne prennent pas la valeur $-\infty$ et ne sont pas identiquement égales à $+\infty$ ),
$\operatorname {C{\overline {onv}}} (\mathbb {E} )$ la partie de $\operatorname {Conv} (\mathbb {E} )$ formée des fonctions qui sont aussi fermées (c'est-à-dire, leur épigraphe est fermé),
$\operatorname {int} \,C$ l'intérieur et $\operatorname {intr} \,C$ l'intérieur relatif d'un convexe $C\subset \mathbb {E}$ .

Définition

La notion de sous-différentiel peut être généralisée à une fonction convexe de plusieurs variables réelles, pouvant également prendre la valeur $+\infty$ . Cette dernière extension trouve son utilité, par exemple en optimisation, lorsque la fonction résulte d'une construction qui n'assure pas a priori la finitude des valeurs qu'elle prend. Comme pour la notion de gradient, on a besoin que l'espace sur lequel est définie la fonction soit muni d'un produit scalaire si l'on veut construire des objets dans cet espace et non dans son dual. Les concepts seront mieux révélés en travaillant sur un espace euclidien abstrait, qui pourra, si on le souhaite, être vu comme $\mathbb {R} ^{n}$ muni du produit scalaire euclidien.

Sous-gradient — Soit $f:\mathbb {E} \to \mathbb {R} \cup \{+\infty \}$ , une fonction convexe et propre. On dit que $s\in \mathbb {E}$ est un sous-gradient de $f$ en $x\in \operatorname {dom} \,f$ si l'une des propriétés équivalentes suivantes est vérifiée :

$\forall \,d\in \mathbb {E} ,~f'(x;d)\geqslant \langle s,d\rangle$ ,
$\forall \,y\in \mathbb {E} ,~f(y)\geqslant f(x)+\langle s,y-x\rangle$ ,
$x$ minimise $y\in \mathbb {E} \mapsto f(y)-\langle s,y\rangle$ ,
$f^{*}(s)+f(x)\leqslant \langle s,x\rangle$ ,
$f^{*}(s)+f(x)=\langle s,x\rangle$ .

La lettre $s$ renvoie à slope (pente) ou sous-gradient (si l'on préfère). La propriété 1 exprime le fait que la fonction $d\in \mathbb {E} \mapsto \langle s,d\rangle$ est une minorante linéaire de la fonction dérivée directionnelle $f'(x;\cdot ):d\in \mathbb {E} \mapsto f'(x;d)\in \mathbb {R} \cup \{\pm \infty \}$ (que l'on sait toujours exister lorsque $f$ est convexe), exacte en $0$ . La propriété 2 exprime le fait que la fonction $y\in \mathbb {E} \mapsto f(x)+\langle s,y-x\rangle$ est une minorante affine de $f$ exacte en $x$ . Les propriétés 4 et 5 expriment la même chose que la propriété 2 en utilisant la fonction conjuguée $f^{*}$ de $f$ .

Sous-différentiel — L'ensemble des sous-gradients de $f$ en $x$ est appelé le sous-différentiel de $f$ en $x$ . Il est noté

$\partial f(x).$

On dit que $f$ est sous-différentiable en $x$ si $\partial f(x)\neq \varnothing$ . Par convention, $\partial f(x)=\varnothing$ si $x\notin \operatorname {dom} \,f$ .

Propriétés

Optimalité

La propriété 2 de la définition du sous-différentiel permet d'obtenir immédiatement une expression simple de l'optimalité d'un point.

Condition d'optimalité — Soit $f\in \operatorname {Conv} (\mathbb {E} )$ . Un point ${\bar {x}}\in \mathbb {E}$ minimise $f$ sur $\mathbb {E}$ si, et seulement si, $0\in \partial f({\bar {x}})$ .

Cette condition nécessaire et suffisante d'optimalité du premier ordre (ainsi qualifiée parce qu'elle ne fait intervenir que les « dérivées » premières de la fonction) est typique des problèmes d'optimisation convexes (voir la section Conditions du premier ordre sans contrainte de l'article Conditions d'optimalité).

Trouver les minimiseurs d'une fonction convexe propre revient donc à trouver les « zéros » de son sous-différentiel. Ce résultat est à rapprocher de celui selon lequel les minimiseurs d'une fonction convexe différentiable sont les points qui annulent son gradient. Ce résultat est plus riche qu'il ne paraît à première vue. En effet, du fait que la fonction peut prendre la valeur $+\infty$ , il traite également de la minimisation d'une fonction convexe sous contraintes convexes (l'ensemble admissible étant le domaine de la fonction).

Lorsque $f$ est polyédrique, on a les caractérisations supplémentaires suivantes[2], liées au concept de minimum saillant.

Caractérisations de l'intériorité relative et de l'unicité d'un minimiseur de fonction polyédrique — Soit $f\in \operatorname {C{\overline {onv}}} (\mathbb {E} )$ une fonction polyédrique. Alors

{\begin{array}{rcl}{\bar {x}}\in \operatorname {intr} {\bigl (}\operatorname {arg\,min} \,f{\bigr )}&\Longleftrightarrow &0\in \operatorname {intr} {\bigl (}\partial f({\bar {x}}){\bigr )},\\\operatorname {arg\,min} \,f=\{{\bar {x}}\}&\Longleftrightarrow &0\in \operatorname {int} {\bigl (}\partial f({\bar {x}}){\bigr )}.\end{array}}

La polyédricité de la fonction joue un rôle majeur dans les caractérisations précédentes. Ainsi chacune des implications de la première équivalence peut être fausse pour une fonction non polyédrique : l'implication " $\Rightarrow$ " est fausse pour la fonction $x\in \mathbb {R} \to \max(x^{2},x)$ en ${\bar {x}}=0$ et l'implication " $\Leftarrow$ " est fausse pour la fonction $x\in \mathbb {R} \to \max(0,x)^{2}$ en ${\bar {x}}=0$ . Pour la seconde équivalence, l'implication " $\Rightarrow$ " est fausse pour la fonction $x\in \mathbb {R} \to x^{2}$ en ${\bar {x}}=0$ , mais l'implication " $\Leftarrow$ " reste vraie même si $f$ n'est pas polyédrique.

Règle de bascule

Les sous-différentiels de $f$ et de sa conjuguée $f^{*}$ jouissent d'une belle règle de réciprocité, parfois appelée règle de bascule[3].

Règle de bascule —

Si $f\in \operatorname {Conv} (\mathbb {E} )$ , alors $s\in \partial f(x)\;\Longrightarrow x\in \partial f^{*}(s)$ .
Si $f\in \operatorname {C{\overline {onv}}} (\mathbb {E} )$ , alors $s\in \partial f(x)\Longleftrightarrow x\in \partial f^{*}(s)$ .

La réciproque n'a pas lieu au point 1, pour la fonction $f\in \operatorname {Conv} (\mathbb {R} )$ ci-dessous

f(x)=\left\{{\begin{array}{lll}0&{\mbox{si}}&x<0\\1&{\mbox{si}}&x=0\\+\infty &{\mbox{si}}&x>0\end{array}}\right.\qquad {\mbox{donc}}\qquad f^{*}(s)=\left\{{\begin{array}{lll}+\infty &{\mbox{si}}&s<0\\0&{\mbox{si}}&s\geq 0,\end{array}}\right.

puisque l'on a $0\notin \partial f(0)=\varnothing$ , alors que $0\in \partial f^{*}(0)={]-\infty ,0]}$ .

Sous-différentiabilité

Rappelons que l'on dit que $f\in \operatorname {Conv} (\mathbb {E} )$ est sous-différentiable en $x\in \operatorname {dom} \,f$ si $\partial f(x)\neq \varnothing$ . Affirmer qu'un ensemble est non vide est une propriété forte qui, dans certains cas, revient à montrer qu'un certain problème a une solution.

La propriété 1 définissant un sous-gradient $s$ , à savoir

$\forall \,d\in \mathbb {E} ,\quad f'(x;d)\geqslant \langle s,d\rangle ,$

montre clairement que $f$ ne peut être sous-différentiable en $x$ si la dérivée directionnelle $f'(x;\cdot )$ prend en une direction la valeur $-\infty$ puisque le membre de droite de l'inégalité ci-dessus est toujours fini. La réciproque de cette observation est le sujet de la proposition qui suit. Une telle situation se présente pour la fonction convexe définie par

$f(x)=\left\{{\begin{array}{ll}-{\sqrt {x}}&{\mbox{si}}~x\geqslant 0\\+\infty &{\mbox{sinon}}.\end{array}}\right.$

Cette fonction n'est pas sous-différentiable en zéro, parce que $f'(0;1)=-\infty$ . Évidemment, si $f'(x;d)=-\infty$ , alors $f'(x;-d)=+\infty$ , mais ce n'est pas la valeur $+\infty$ de la dérivée directionnelle qui empêche $f$ d'être sous-différentiable en $x$ . C'est ce que montre la fonction indicatrice de l'intervalle $[0,+\infty [$ , dont le sous-différentiel en zéro est l'intevalle ${]-\infty ,0]}$ .

Sous-différentiabilité — Si $f\in \operatorname {Conv} (\mathbb {E} )$ et $x\in \mathbb {E}$ , les propriétés suivantes sont équivalentes :

$f$ est sous-différentiable en $x$ ,
il existe $y\in \operatorname {intr} \,(\operatorname {dom} \,f)$ tel que $f'(x;y-x)>-\infty$ ,
$f'(x;\cdot )$ ne prend pas la valeur $-\infty$ .

Ces propriétés sont vérifiées si $x\in \operatorname {intr} \,(\operatorname {dom} \,f)$ .

Propriétés géométriques et topologiques

On note ci-dessous $\operatorname {aff} \,P$ l'enveloppe affine d'une partie $P\subset \mathbb {E}$ .

Propriétés géométriques et topologiques du sous-différentiel — Soient $f\in \operatorname {Conv} (\mathbb {E} )$ , $\mathbb {E} _{0}$ le sous-espace vectoriel parallèle à $\operatorname {aff} \,(\operatorname {dom} \,f)$ , $P_{\mathbb {E} _{0}}$ le projecteur orthogonal sur $\mathbb {E} _{0}$ et $x\in \operatorname {dom} \,f$ . On note $f|_{x+\mathbb {E} _{0}}$ la restriction de $f$ à $x+\mathbb {E} _{0}=\operatorname {aff} \,(\operatorname {dom} \,f)$ . Alors

$\partial f(x)=\partial f|_{x+\mathbb {E} _{0}}(x)+\mathbb {E} _{0}^{\perp }$ , en particulier $P_{\mathbb {E} _{0}}\partial f(x)=\partial f|_{x+\mathbb {E} _{0}}(x)$ ,
$\partial f(x)$ est convexe et fermé (éventuellement vide),
$x\in \operatorname {intr} \,(\operatorname {dom} \,f)~\Longleftrightarrow ~P_{\mathbb {E} _{0}}\partial f(x)$ est non vide et borné,
$x\in \operatorname {int} \,(\operatorname {dom} \,f)~\Longleftrightarrow ~\partial f(x)$ est non vide et borné.

Si $f$ ne prend que des valeurs réelles, alors $\operatorname {dom} \,f=\mathbb {E}$ et son sous-différentiel est un ensemble non vide, convexe et compact (par les points 2 et 4).

Formule du max

Le sous-différentiel peut être défini en utilisant la dérivée directionnelle (propriété 1 de la définition). La proposition suivante montre que l'on peut retrouver les dérivées directionnelles à partir du sous-différentiel : $f'(x;\cdot )$ est la fonction d'appui de $\partial f(x)$ .

Formule du max — Si $f\in \operatorname {Conv} (\mathbb {E} )$ et $x\in \operatorname {intr} \,(\operatorname {dom} \,f)$ , alors

$\forall \,d\in \mathbb {E$

Le supremum est atteint si $f'(x;d)<+\infty$ .

Le résultat précédent ne tient plus si $x$ est sur la frontière relative du domaine de $f$ . Voici un contre-exemple : $f$ est l'indicatrice de la boule-unité fermée de $\mathbb {R} ^{2}$ , pour la norme euclidienne, et $x=(-1,0)$ . Alors $f'(x;0)=0$ et si $d\neq 0$ :

$f'(x;d)=\left\{{\begin{array}{lll}0&{\mbox{si}}&d_{1}>0\\+\infty &{\mbox{si}}&d_{1}\leqslant 0.\end{array}}\right.$

Dès lors, la fonction $\delta _{x}:d\mapsto f'(x;d)$ n'est pas fermée et ne peut donc être la fonction d'appui d'un ensemble, en particulier elle n'est pas la fonction d'appui du sous-différentiel. D'ailleurs, ce dernier s'écrit $\partial f(x)=\{s\in \mathbb {R} ^{2}:s_{1}\leqslant 0,~s_{2}=0\}$ et

$\sigma _{\partial f(x)}(d)=\left\{{\begin{array}{lll}0&{\mbox{si}}&d_{1}\geqslant 0\\+\infty &{\mbox{si}}&d_{1}<0\end{array}}\right.$

est l'enveloppe convexe fermée de $\delta _{x}$ . Cette propriété est tout à fait générale pour les fonctions de $\operatorname {C{\overline {onv}}} (\mathbb {E} )$ .

La multifonction sous-différentiel

On peut voir $\partial f$ comme une multifonction ou fonction multivoque, qui à un élément de $\mathbb {E}$ fait correspondre une partie de $\mathbb {E}$ , c'est-à-dire un élément de l'ensemble ${\mathcal {P}}(\mathbb {E} )$ des parties de $\mathbb {E}$ . On note

$\partial f:\mathbb {E} \multimap \mathbb {E} :x\mapsto \partial f(x)$

cette correspondance.

Rappelons quelques notions d'analyse multifonctionnelle. Soit ${\displaystyle \varphi$ une multifonction. On définit le domaine, l'image et le graphe de $\varphi$ respectivement par

${\begin{array}{rcl}\operatorname {dom} \,\varphi &:=&\{x\in \mathbb {E$

On notera bien que l'on a choisi de définir le graphe comme une partie de $\mathbb {E} \times \mathbb {F}$ et pas de $\mathbb {E} \times {\mathcal {P}}(\mathbb {F} )$ . La multifonction réciproque $\varphi ^{-1}:\mathbb {F} \multimap \mathbb {E}$ de la multifonction ${\displaystyle \varphi$ est définie en $u\in \mathbb {F}$ par

$\varphi ^{-1}(u)=\{x\in \mathbb {E} :u\in \varphi (x)\}.$

Lorsque $\mathbb {E}$ est un espace euclidien dont le produit scalaire est noté $\langle \cdot ,\cdot \rangle$ et que $\mathbb {F} =\mathbb {E}$ , on dit que $\varphi$ est monotone si

$\forall \,(x,u)\in {\mathcal {G}}(\varphi ),~~\forall \,(y,v)\in {\mathcal {G}}(\varphi ):\qquad \langle v-u,y-x\rangle \geqslant 0.$

On dit que $\varphi$ est monotone maximale si $\varphi$ est monotone et si son graphe n'est pas strictement contenu dans le graphe d'un opérateur monotone. On vérifie facilement que cette dernière propriété s'écrit aussi

${\Bigl [}\langle v-u,y-x\rangle \geqslant 0,\quad \forall \,(x,u)\in {\mathcal {G}}(\varphi ){\Bigr ]}\quad \Longrightarrow \quad (y,v)\in {\mathcal {G}}(\varphi ).$

Dans le résultat ci-dessous, on note $f^{*}$ la conjuguée de $f$ .

La multifonction sous-différentiel — Si $f\in \operatorname {Conv} (\mathbb {E} )$ , alors

$\operatorname {intr} \,(\operatorname {dom} \,f)\subset \operatorname {dom} \,\partial f\subset \operatorname {dom} \,f$ ;
${\mathcal {R}}(\partial f)\subset \operatorname {dom} \,f^{*}$ ;
${\mathcal {G}}(\partial f)$ est fermé ;
la multifonction $\partial f$ est monotone.

Si $f\in \operatorname {C{\overline {onv}}} (\mathbb {E} )$ , alors

$\operatorname {intr} \,(\operatorname {dom} \,f^{*})\subset {\mathcal {R}}(\partial f)$ ;
$(\partial f)^{-1}=\partial f^{*}$ ;
la multifonction $\partial f$ est monotone maximale.

On rappelle que $f:\mathbb {E} \to \mathbb {R} \cup \{+\infty \}$ est fortement convexe, de module $\alpha >0$ , si pour tout $x_{0}$ et $x_{1}\in \operatorname {dom} \,f$ et pour tout $t\in [0,1]\subset \mathbb {R}$ , on a

$f((1-t)x_{0}+tx_{1})\leq (1-t)f(x_{0})+tf(x_{1})-{\frac {\alpha }{2}}\,t(1-t)\|x_{0}-x_{1}\|^{2}.$

Rappelons aussi qu'une multifonction ${\displaystyle \varphi$ est dit fortement monotone, de module $\alpha >0$ , si

$\forall \,(x,y)\in {\mathcal {G}}(\varphi ),\quad \forall \,(x',y')\in {\mathcal {G}}(\varphi ):\qquad \langle y-y',x-x'\rangle \geqslant \alpha \|x-x'\|^{2}.$

La forte convexité de $f$ peut s'exprimer par la forte monotonie de $\partial f$ [4].

Sous-différentiel fortement monotone — Pour une fonction $f:\mathbb {E} \to \mathbb {R} \cup \{+\infty \}$ et un réel $\alpha >0$ , les propriétés suivantes sont équivalentes :

$f$ est fortement convexe de module $\alpha$ ,
$\partial f$ est fortement monotone de module $\alpha$ ,
$\forall \,(x,s)\in {\mathcal {G}}(\partial f)$ et $\forall \,y\in \mathbb {E}$ , on a
$f(y)\geqslant f(x)+\langle s,y-x\rangle +{\frac {\alpha }{2}}\|y-x\|^{2}.$

Lien avec la différentiabilité

Rappelons les trois notions de différentiabilité d'une fonction $f:\mathbb {E} \to {\bar {\mathbb {R} }}$ dont il est question dans cette section. On suppose que $f$ est finie au point $x$ où sont prises ces dérivées.

On dit que $f$ a une dérivée partielle en $x$ suivant un vecteur $d\in \mathbb {E}$ si la fonction $t\in \mathbb {R} \mapsto f(x+td)$ est différentiable en $t=0$ .
On dit que $f$ est Gâteaux-différentiable en $x$ si la dérivée directionnelle $f'(x;d)$ existe pour tout $d\in \mathbb {E}$ et si $d\in \mathbb {E} \mapsto f'(x;d)$ est linéaire.
On dit que $f$ est Fréchet-différentiable en $x$ s'il existe un vecteur $D\in \mathbb {E}$ tel que
$\lim _{h\to 0 \atop h\neq 0}{\frac {f(x+h)-f(x)-\langle D,h\rangle }{\|h\|}}=0.$
Dans ce cas, le vecteur $D$ est appelé le gradient de $f$ en $x$ . On le note
$\nabla f(x).$
D'après la définition, si $f$ est Fréchet-différentiable en $x$ , $f$ prend des valeurs finies dans un voisinage de $x$ .

Ces trois propriétés sont de plus en plus fortes (la Fréchet-différentiabilité implique la Gâteaux-différentiabilité, qui implique elle-même la différentiabilité partielle). Pour une fonction convexe, les trois notions sont équivalentes[5], si bien qu'il n'y a alors pas lieu de faire de distinction entre celles-ci.

Gâteaux et Fréchet différentiabilité — Soient $f\in \operatorname {Conv} (\mathbb {E} )$ et $x\in (\operatorname {dom} \,f)^{\circ }$ . On note $n$ la dimension de $\mathbb {E}$ . Alors les propriétés suivantes sont équivalentes :

$f$ a des dérivées partielles en $x$ suivant $n$ directions linéairement indépendantes,
$f$ est Gâteaux-différentiable en $x$ ,
$f$ est Fréchet-différentiable en $x$ .

Le résultat suivant[6] établit un lien entre la différentiabilité et la sous-différentiabilité : en bref, une fonction est différentiable en un point si, et seulement si, elle est sous-différentiable en ce point et son sous-différentiel est un singleton.

Différentiabilité et sous-différentiabilité — Soient $f\in \operatorname {Conv} (\mathbb {E} )$ et $x\in (\operatorname {dom} \,f)^{\circ }$ .

Si $f$ est différentiable en $x$ , alors $\partial f(x)=\{\nabla f(x)\}$ .
Si $\partial f(x)$ est le singleton $\{D\}$ , alors $f$ est différentiable en $x$ et $\nabla f(x)=D$ .

Combinaison conique

Voici une conséquence immédiate de la définition du sous-différentiel.

Multiplication par un scalaire positif — Soit $\alpha \geqslant 0$ , $f\in \operatorname {Conv} (\mathbb {E} )$ et $x\in \mathbb {E}$ . Alors

$\partial (\alpha f)(x)=\alpha \,\partial f(x).$

On remarquera bien que le scalaire multiplie une fonction dans le membre de gauche de l'identité ci-dessus et un ensemble dans son membre de droite.

À l'inverse, comme le montrera un exemple ci-dessous, l'égalité entre le sous-différentiel de la somme de fonctions convexes et la somme des sous-différentiels n'est pas nécessairement assurée. On aura certainement l'égalité si toutes les fonctions ne prennent que des valeurs finies. On notera également que la somme se fait sur des fonctions dans le membre de gauche de l'identité et sur des ensembles dans celui de droite.

Sous-différentiel d'une somme — Soient $f_{1},\ldots ,f_{p}\in \operatorname {Conv} (\mathbb {E} )$ et $x\in \mathbb {E}$ . Alors

$\partial (f_{1}+\cdots +f_{p})(x)\supset \partial f_{1}(x)+\cdots +\partial f_{p}(x),$

avec égalité si

$\bigcap _{1\leqslant i\leqslant p}\,\operatorname {intr} \,(\operatorname {dom} \,f_{i})\neq \varnothing .$

Dans cette dernière condition, on peut remplacer $\operatorname {intr} \,(\operatorname {dom} \,f_{i})$ par $\operatorname {dom} \,f_{i}$ si $f_{i}$ est polyédrique.

Voici un exemple où l'égalité n'est pas assurée dans la formule de la somme ( $f_{2}$ est la fonction indicatrice de ${]-\infty ,0]}$ ):

$f_{1}:x\in \mathbb {R} \mapsto \left\{{\begin{array}{ll}-{\sqrt {x}}&{\mbox{si}}~x\geqslant 0\\+\infty &{\mbox{sinon}}\end{array}}\right.\qquad {\mbox{et}}\qquad f_{2}={\mathcal {I}}_{]-\infty ,0]}.$

Comme la somme $f=f_{1}+f_{2}$ est l'indicatrice de $\{0\}$ , on a $\partial f(0)=\mathbb {R}$ , alors que $\partial f_{1}(0)+\partial f_{2}(0)=\varnothing$ , parce que $\partial f_{1}(0)=\varnothing$ .

Pré-composition par une fonction affine

Le cadre est le suivant. On dispose d'une fonction affine $a:\mathbb {E} \to \mathbb {F}$ entre deux espaces euclidiens $\mathbb {E}$ et $\mathbb {F}$ . Celle-ci est supposée être définie en $x\in \mathbb {E}$ par

$a(x)=Ax+b,$

où $A:\mathbb {E} \to \mathbb {F}$ est linéaire et $b\in \mathbb {F}$ . On note ${\mathcal {R}}(a):=a(\mathbb {E} )$ l'Image directe de $\mathbb {E}$ par $a$ et $A^{*}$ l'application linéaire adjointe de $A$ pour les produits scalaires que l'on s'est donnés sur $\mathbb {E}$ et $\mathbb {F}$ , défini donc par la relation

$\forall \,x\in \mathbb {E} ,\quad \forall \,y\in \mathbb {F$

L'application affine $a$ est composée avec une application $g:\mathbb {F} \to {\bar {\mathbb {R} }}$ .

Sous-différentiel d'une pré-composition par une fonction affine — Dans le cadre défini ci-dessus, si $g\in \operatorname {Conv} (\mathbb {F} )$ , alors pour tout $x\in \mathbb {E}$ :

$\partial (g\circ a)(x)\supset A^{*}{\Bigl (}\partial g(a(x)){\Bigr )},$

avec égalité si l'une des conditions suivantes est vérifiée :

${\mathcal {R}}(a)\cap \operatorname {intr} \,(\operatorname {dom} \,g)\neq \varnothing$ ,
${\mathcal {R}}(a)\cap \operatorname {dom} \,g\neq \varnothing$ et $g$ est polyédrique.

Fonction marginale

Soient $\mathbb {E}$ et $\mathbb {F}$ deux espaces euclidiens et ${\displaystyle \varphi$ une fonction. On associe à cette dernière la fonction marginale $f:\mathbb {E} \to {\bar {\mathbb {R} }}$ définie par :

$f(x)=\inf _{y\in \mathbb {F} }\varphi (x,y).$

Le sous-différentiel de $f$ dépend de celui de $\varphi$ qui est supposé calculé pour le produit scalaire de $\mathbb {E} \times \mathbb {F}$ suivant : $\langle (x,y),(x',y')\rangle =\langle x,x'\rangle +\langle y,y'\rangle$ .

Sous-différentiel d'une fonction marginale — Dans le cadre défini ci-dessus, supposons que $\varphi \in \operatorname {Conv} (\mathbb {E} \times \mathbb {F} )$ et que $f\in \operatorname {Conv} (\mathbb {E} )$ . Si $x\in \mathbb {E}$ et $f(x)=\varphi (x,y)$ (l'infimum est atteint en $y\in \mathbb {F}$ ), alors

$\partial f(x)=\{s:(s,0)\in \partial \varphi (x,y)\}.$

Ce résultat appelle quelques remarques.

Il faut bien noter que, si la borne inférieure $\inf\{\varphi (x,y):y\in \mathbb {F} \}$ est atteinte en plusieurs $y$ , $\{s:(s,0)\in \partial \varphi (x,y)\}$ ne dépend pas du minimiseur $y$ choisi.

On a un autre éclairage sur cette indépendance par rapport à $y$ en observant que $\varphi$ est constante sur l'ensemble $M(x):=\{(x,y):$ $y$ minimise $\varphi (x,\cdot )\}$ , si bien que $\partial \varphi$ est aussi constant sur l'intérieur relatif de $M(x)$ . Cependant $\partial \varphi (x,y)$ peut varier lorsque $(x,y)$ passe de l'intérieur relatif de $M(x)$ à son bord. C'est le cas de la fonction définie par $\varphi (x,y)=\max(0,|y|-1)$ , dont la fonction marginale est nulle :

$M(x)=\{x\}\times [-1,1]\quad {\mbox{et}}\quad \partial \varphi (0,y)=\left\{{\begin{array}{ll}\{(0,0)\}&{\mbox{si}}~-1<y<1\\\{0\}\times [0,1]&{\mbox{si}}~y=1.\end{array}}\right.$
D'autre part, si $\varphi$ est différentiable en $(x,y)$ , où $y$ est un minimiseur quelconque de $\varphi (x,\cdot )$ , alors $f$ est également différentiable en $x$ (car son sous-différentiel est un singleton) et on a

$\nabla f(x)=\nabla _{x}\varphi (x,y).$
C'est comme s'il y avait un minimiseur unique $y(x)$ , fonction différentiable de $x$ , que l'on écrivait $f(x)=\varphi (x,y(x))$ et que l'on calculait $\nabla f(x)$ par une dérivation en chaîne :

$\nabla f(x)=\nabla _{x}\varphi (x,y)+y'(x)^{*}\nabla _{y}\varphi (x,y).$
On retrouverait le résultat ci-dessus en observant que $\nabla _{y}\varphi (x,y)=0$ car $y$ minimise $\varphi (x,\cdot )$ .
Le fait que $\varphi (x,\cdot )$ ait un minimum unique n'implique nullement la différentiabilité de la fonction marginale en $x$ . Par exemple, $f$ est la fonction marginale de $\varphi$ définie par $\varphi (x,y)=f(x)+y^{2}$ . Cette dernière a un minimum $y=0$ unique en $y$ quel que soit $x$ , alors que $f$ peut ne pas être différentiable.

Fonctions concave et convexe-concave

Certaines constructions conduisent naturellement à des fonctions concaves plutôt que convexes. Il en est ainsi, par exemple, lorsque l'on prend l'enveloppe inférieure d'une famille de fonctions linéaires (la fonction duale d'un problème d'optimisation est construite de cette manière). On peut alors prendre le sous-différentiel de la fonction opposée, qui est convexe, mais il est parfois plus naturel de se passer de la multiplication par moins un. Si $f$ est concave, on définit donc le sous-différentiel concave de cette fonction en un point $x$ où elle est finie, comme l'ensemble noté et défini par

${\overset {\frown }{\partial }}f(x):=-\partial (-f)(x).$

Certains auteurs ne mettent pas le signe $\frown$ au-dessus de $\partial$ ; il faut alors se rappeler que $f$ est concave. Si $f$ est concave différentiable, son sous-différentiel concave se réduit bien au gradient de $f$ . Les propriétés suivantes sont équivalentes :

$s\in {\overset {\frown }{\partial }}f(x)$ ,
$\forall \,d\in \mathbb {E} ,~f'(x;d)\leqslant \langle s,d\rangle$ ,
$\forall \,y\in \mathbb {E} ,~f(y)\leqslant f(x)+\langle s,y-x\rangle$ ,
$x$ maximise $y\in \mathbb {E} \mapsto f(y)-\langle s,y\rangle$ .

Il est aussi intéressant de définir le sous-différentiel d'une fonction convexe-concave. Si $\mathbb {E}$ et $\mathbb {F}$ sont deux espaces vectoriels, on dit que $f:\mathbb {E} \times \mathbb {F} \to {\bar {\mathbb {R} }}$ est convexe-concave si

pour tout $y\in \mathbb {F}$ , $x\mapsto f(x,y)$ est convexe et
pour tout $x\in \mathbb {E}$ , $y\mapsto f(x,y)$ est concave.

Le lagrangien d'un problème d'optimisation convexe avec contraintes a cette propriété. La situation est plus complexe que dans le cas d'une fonction concave, car il ne suffit pas de multiplier (une partie de) la fonction par $-1$ pour retrouver une fonction convexe et lui appliquer la notion de sous-différentiel convexe que l'on connait.

Sous-gradient d'une fonction convexe-concave — Soient $\mathbb {E}$ et $\mathbb {F}$ deux espaces vectoriels et $f:\mathbb {E} \times \mathbb {F} \to {\bar {\mathbb {R} }}$ une fonction convexe-concave. On dit que $(u,v)\in \mathbb {E}$ est un sous-gradient (convexe-concave) de $f$ en un point $(x,y)$ où $f$ prend une valeur finie si $(u,v)$ vérifie l'une des propriétés équivalentes suivantes :

$u\in \partial _{x}f(x,y)$ et $v\in {\overset {\frown }{\partial }}_{y}f(x,y)$ ,
$\forall \,x'\in \mathbb {E$ ,
$\forall \,y'\in \mathbb {F$ ,
$(x,y)$ est un point-selle de $(x',y')\in \mathbb {E} \times \mathbb {F} \mapsto f(x',y')-\langle u,x'\rangle -\langle v,y'\rangle$ .

On note ${\overset {\backsim }{\partial }}f(x,y)$ l'ensemble des sous-gradients et on le nomme le sous-différentiel (convexe-concave) de $f$ . Par convention, ce sous-différentiel est vide si $f(x)$ n'est pas fini.

De manière synthétique :

{\overset {\backsim }{\partial }}f(x,y):=\partial _{x}f(x,y)\times {\overset {\frown }{\partial }}_{y}f(x,y).

Dans cette définition, on a noté $\partial _{x}f(x,y)$ le sous-différentiel ordinaire en $x$ de la fonction convexe $x'\mapsto f(x',y)$ et ${\overset {\frown }{\partial }}_{y}f(x,y)$ le sous-différentiel concave en $y$ de la fonction concave $y'\mapsto f(x,y')$ . Certains auteurs ne mettent pas le signe $\backsim$ au-dessus de $\partial$ ; il faut alors se rappeler que $f$ est convexe-concave.

Exemples

Voici quelques exemples de sous-différentiels de fonctions convexes classiques.

Fonction indicatrice

On suppose ici que $\mathbb {E}$ est un espace euclidien et que $C$ est un convexe de $\mathbb {E}$ .

Le sous-différentiel de la fonction indicatrice ${\mathcal {I}}_{C}$ est le cône normal $N_{C}$ de $C$ :

\partial \,{\mathcal {I}}_{C}=N_{C}.

Norme

Soit $\|\cdot \|$ une norme sur un espace euclidien $\mathbb {E}$ , non nécessairement dérivée du produit scalaire $\langle \cdot ,\cdot \rangle$ de $\mathbb {E}$ . On introduit la norme duale

$\|s\|_{_{D}}:=\sup _{\|x\|\leqslant 1}\;\langle s,x\rangle$

et la boule-unité duale fermée

${\bar {B}}_{_{D}}:=\{s\in \mathbb {E$

Une norme est évidemment une fonction convexe (par l'inégalité triangulaire), partout sous-différentiable (elle ne prend que des valeurs finies). Son sous-différentiel est donné par les formules

\partial (\|\cdot \|)(x)=\operatorname {arg\,max} _{s\in {\bar {B}}_{_{D}}}\,\langle s,x\rangle =\{s\in {\bar {B}}_{_{D}}:\langle s,x\rangle =\|x\|\}.

En particulier :

si $x\neq 0$ , les sous-gradients $s\in \partial (\|\cdot \|)(x)$ sont sur la frontière de ${\bar {B}}_{_{D}}$ : $\|s\|_{_{D}}=1$ ;
$\partial (\|\cdot \|)(0)={\bar {B}}_{_{D}}$ .

La puissance $p>1$ d'une norme

$f:\mathbb {E} \to \mathbb {R} :x\mapsto f(x):={\frac {1}{p}}\,\|x\|^{p}$

est aussi une fonction convexe (composition de fonctions convexes dont la seconde est croissante) propre (elle ne prend que des valeurs finies) fermée (elle est continue) et partout sous-différentiable (elle ne prend que des valeurs finies). Son sous-différentiel est donné par les formules

\partial f(x)=\{s\in \mathbb {E

où $p':=p/(p-1)\in {]0,1[}$ est le nombre conjugué de $p$ :

${\frac {1}{p}}+{\frac {1}{p'}}=1.$

La dernière expression du sous-différentiel $\partial f(x)$ rappelle la dérivation en chaîne de la composition de $x\in \mathbb {E} \mapsto \|x\|$ et de $t\in \mathbb {R} \mapsto t^{p}/p$ .

Distance à un convexe

Soit $\|\cdot \|$ une norme sur un espace euclidien $\mathbb {E}$ , non nécessairement dérivée du produit scalaire $\langle \cdot ,\cdot \rangle$ de $\mathbb {E}$ . On introduit la norme duale

$\|s\|_{_{D}}:=\sup _{\|x\|\leqslant 1}\;\langle s,x\rangle$

et la boule-unité duale fermée

${\bar {B}}_{_{D}}:=\{s\in \mathbb {E$

Soit $C$ un ensemble convexe fermé non vide de $\mathbb {E}$ . On considère la fonction $\operatorname {dist} _{C}:\mathbb {E} \to \mathbb {R}$ , la distance à $C$ , définie par

$\operatorname {dist} _{C}(x)=\inf _{y\in C}\|x-y\|.$

C'est une fonction convexe propre et fermée (elle ne prend que des valeurs finies). On note ${\bar {x}}$ une projection d'un point $x$ sur $C$ : c'est une solution du problème $\inf\{\|x-y\|:y\in C\}$ . Cette dernière n'est pas nécessairement unique car la norme n'est pas nécessairement associée à un produit scalaire.

Le sous-différentiel en $x\in \mathbb {E}$ de la distance à $C$ est donné par la formule

\partial \,\operatorname {dist} _{C}(x)=\left\{s\in {\bar {B}}_{_{D}}\cap N_{C}({\bar {x}}):\langle s,x-{\bar {x}}\rangle =\|x-{\bar {x}}\|\right\}.

où $N_{C}(x):=\{d\in \mathbb {E$ pour tout $y\in C\}$ est le cône normal à $C$ en $x$ .

Lorsque la norme $\|\cdot \|$ est celle associée au produit scalaire $\langle \cdot ,\cdot \rangle$ , les boules-unités primale et duale coïncident (c'est-à-dire, ${\bar {B}}_{_{D}}={\bar {B}}$ ) et on a les propriétés suivantes :

si $x\notin C$ , alors $\operatorname {dist} _{C}$ est différentiable en $x$ et $\nabla \operatorname {dist} _{C}(x)=(x-{\bar {x}})/{\|x-{\bar {x}}\|}$ ;
si $x\in \operatorname {int} \,C$ , l'intérieur de $C$ , alors $\operatorname {dist} _{C}$ est différentiable en $x$ et $\nabla \operatorname {dist} _{C}(x)=0$ ;
si $x\in C\setminus (\operatorname {int} \,C)$ , la frontière de $C$ , alors $\partial \,\operatorname {dist} _{C}(x)={\bar {B}}\cap N_{C}(x)$ .

En l'absence de convexité d'un ensemble $P\subset \mathbb {E}$ , la distance $\operatorname {dist} _{P}$ n'est pas nécessairement différentiable sur le complémentaire de $P$ .

Valeur propre maximale

On note ${\mathcal {S}}^{n}$ l'ensemble des matrices réelles d'ordre $n$ symétriques, que l'on munit du produit scalaire canonique ${\displaystyle (A,B)\in {\mathcal {S}}^{n}\times {\mathcal {S}}^{n}\mapsto \langle A,B\rangle$ ( $\operatorname {tr} \,A$ désigne la trace de la matrice $A$ ). On note aussi ${\mathcal {S}}_{+}^{n}$ le cône de ${\mathcal {S}}^{n}$ formé des matrices semi-définies positives. On note enfin

$\lambda _{1}:{\mathcal {S}}^{n}\to \mathbb {R} :A\mapsto \lambda _{1}(A)$

l'application valeur propre maximale, qui à une matrice symétrique $A$ associe sa plus grande valeur propre (on rappelle qu'une matrice symétrique d'ordre $n$ a $n$ valeurs propres réelles). C'est une fonction propre, convexe et continue (donc fermée). Son sous-différentiel en $A\in {\mathcal {S}}^{n}$ est donné par la formule

\partial \lambda _{1}(A)=\operatorname {co} \,\{vv^{\top \!}:\|v\|_{2}=1,\;Av=\lambda _{1}(A)v\},

où $\operatorname {co} \,P$ désigne l'enveloppe convexe d'un ensemble $P$ . L'enveloppe convexe ci-dessus est compacte (par exemple, parce que le sous-différentiel d'une fonction convexe ne prenant que des valeurs finies, comme $\lambda _{1}$ , l'est).

On en déduit que :

si $\lambda _{1}(A)$ est simple, $\lambda _{1}(\cdot )$ est différentiable en $A$ et son gradient s'écrit alors $\nabla \lambda _{1}(A)=vv^{\top \!},$ où $\pm v$ sont les uniques vecteurs propres unitaires associés à la valeur propre maximale ;
$\partial \lambda _{1}(0)=\{S\in {\mathcal {S}}_{+}^{n}:\operatorname {tr} \,S=1\}$ ;
la dérivée directionnelle de $\lambda _{1}$ en $A\in {\mathcal {S}}^{n}$ dans la direction $D\in {\mathcal {S}}^{n}$ s'écrit $\lambda _{1}'(A;D)=\lambda _{1}(V^{\top \!}DV),$ où $V$ est une matrice dont les colonnes forment une base orthonormale de l'espace propre associé à $\lambda _{1}(A)$ .

Fonction spectrale

La présentation ci-dessous synthétise celles de Lewis (1996), Hiriart-Urruty (1998), Borwein et Lewis (2000).

On note ${\mathcal {S}}^{n}$ l'ensemble des matrices réelles d'ordre $n$ symétriques, que l'on munit du produit scalaire canonique ${\displaystyle (A,B)\in {\mathcal {S}}^{n}\times {\mathcal {S}}^{n}\mapsto \langle A,B\rangle$ , la trace de la matrice $AB$ . Par ailleurs, pour $x\in \mathbb {R} ^{n}$ , on note $[x]\in \mathbb {R} ^{n}$ le vecteur formé des composantes de $x$ en ordre décroissant.

On se donne une fonction $f:\mathbb {R} ^{n}\to {\bar {\mathbb {R} }}$ symétrique, c'est-à-dire qui vérifie

$\forall \,x\in \mathbb {R} ^{n}:\qquad f(x)=f([x]),$

ce qui revient à dire que l'on ne modifie pas la valeur de $f(x)$ en permutant les composantes de $x$ . On note

${\displaystyle \lambda$

la fonction donnant les valeurs propres de $A$ en ordre décroissant :

$\lambda _{1}(A)\geqslant \lambda _{2}(A)\geqslant \cdots \geqslant \lambda _{n}(A).$

On appelle fonction spectrale une fonction de la forme $f\circ \lambda$ , avec $f$ et $\lambda$ comme ci-dessus. Ce sont donc des fonctions définies sur ${\mathcal {S}}^{n}$ , mais dont les valeurs ne dépendent que du spectre des matrices.

On peut alors caractériser la convexité-fermeture de $(f\circ \lambda )$ à partir de celle de $f$ [7].

Convexité-fermeture d'une fonction spectrale — Dans le cadre défini ci-dessus, si $f$ est symétrique, alors

$(f\circ \lambda )\in \operatorname {C{\overline {onv}}} ({\mathcal {S}}^{n})\qquad \Longleftrightarrow \qquad f\in \operatorname {C{\overline {onv}}} (\mathbb {R} ^{n}).$

On peut aussi calculer le sous-différentiel de $(f\circ \lambda )$ à partir de celui de $f$ .

Sous-différentiel d'une fonction spectrale — Dans le cadre défini ci-dessus, si $f\in \operatorname {C{\overline {onv}}} (\mathbb {R} ^{n})$ est symétrique, alors les trois propriétés suivantes, reliant $A$ et $S\in {\mathcal {S}}^{n}$ , sont équivalentes :

$S\in \partial (f\circ \lambda )(A)$ ,
$\lambda (S)\in \partial f(\lambda (A))$ et $\langle S,A\rangle =\lambda (S)^{\top \!}\lambda (A)$ ,
il existe une matrice orthogonale $V$ et des vecteurs $a$ , $s\in \mathbb {R} ^{n}$ tels que

$V^{\top \!}AV=\operatorname {Diag} (a),\qquad V^{\top \!}SV=\operatorname {Diag} (s)\qquad {\mbox{et}}\qquad s\in \partial f(a).$

On peut enfin caractériser la différentiabilité de $(f\circ \lambda )$ à partir de celle de $f$ .

Différentiabilité d'une fonction spectrale — Dans le cadre défini ci-dessus, si $f\in \operatorname {C{\overline {onv}}} (\mathbb {R} ^{n})$ est symétrique, $(f\circ \lambda )$ est différentiable en $A$ si, et seulement si, $f$ est différentiable en $\lambda (A)$ . Dans ce cas, si $V$ est une matrice orthogonale telle que $A=V\;\operatorname {Diag} (\lambda (A))\;V^{\top \!}$ , on a

$\nabla (f\circ \lambda )(A)=V\;\operatorname {Diag} (\nabla f(\lambda (A)))\;V^{\top \!}.$

Les fonctions spectrales sont fréquemment rencontrées. En voici quelques-unes, construites à partir de fonctions $f\in \operatorname {C{\overline {onv}}} (\mathbb {R} ^{n})$ , donnant donc lieu à des fonctions $(f\circ \lambda )\in \operatorname {C{\overline {onv}}} ({\mathcal {S}}^{n})$ . Dans le tableau ci-dessous, les entiers $p$ et $q$ peuvent être choisis arbitrairement dans $\{0,\ldots ,n\}$ , un vecteur de $x\in \mathbb {R} ^{n}$ dont toutes les composantes sont strictement positives est signalé par $x>0$ , une matrice $A$ définie positive est signalée par $A\succ 0$ .

$f(x)$	$(f\circ \lambda )(A)$
$[x]_{1}=\max(x_{1},\ldots ,x_{n})$	$\lambda _{1}(A)$
$-[x]_{n}=-\min(x_{1},\ldots ,x_{n})$	$-\lambda _{n}(A)$
$\sum _{i=1}^{p}[x]_{i}-\sum _{i=n-q+1}^{n}[x]_{i}$	$\sum _{i=1}^{p}\lambda _{i}(A)-\sum _{i=n-q+1}^{n}\lambda _{i}(A)$
$\operatorname {l\!b} (x)=\left\{{\begin{array}{ll}-\sum _{i=1}^{n}\log \,x_{i}&{\mbox{si}}~x>0\\+\infty &{\mbox{sinon}}\end{array}}\right.$	$\operatorname {l\!d} (A)=\left\{{\begin{array}{ll}-\log \,\det \,A&{\mbox{si}}~A\succ 0\\+\infty &{\mbox{sinon}}\end{array}}\right.$
$\left\{{\begin{array}{ll}-\left(\sum _{i=1}^{n}\,x_{i}^{-1}\right)^{-1}&{\mbox{si}}~x>0\\+\infty &{\mbox{sinon}}\end{array}}\right.$	$\left\{{\begin{array}{ll}-\left(\operatorname {tr} \,A^{-1}\right)^{-1}&{\mbox{si}}~A\succ 0\\+\infty &{\mbox{sinon}}\end{array}}\right.$

Fonction définie sur un espace localement convexe

La présentation ci-dessous synthétise celle de Bonnans et Shapiro (2000).

Cadre

On suppose donnés deux espaces espaces vectoriels topologiques localement convexes $\mathbb {E}$ et $\mathbb {E} ^{*}$ sur $\mathbb {R}$ couplés, dans le sens où il existe une application bilinéaire continue

${\displaystyle \langle \cdot ,\cdot \rangle$

telle que

le dual topologique de $\mathbb {E}$ coïncide avec $\{\langle \cdot ,x^{*}\rangle :x^{*}\in \mathbb {E} ^{*}\}$ ,
le dual topologique de $\mathbb {E} ^{*}$ coïncide avec $\{\langle x,\cdot \rangle :x\in \mathbb {E} \}$ .

Comme exemples de tels couples d'espaces vectoriels topologiques localement convexes, citons

un espace de Banach et son dual topologique muni de la topologie faible,
un espace vectoriel normé réflexif et son dual topologique muni de la topologie forte.

Définitions

Les définitions de sous-gradient, de sous-différentiel et de sous-différentiabilité sont essentiellement les mêmes que celles introduites en dimension finie.

Sous-gradient, sous-différentiel, sous-différentiabilité — Soit $f:\mathbb {E} \to \mathbb {R} \cup \{+\infty \}$ , une fonction convexe et propre. On dit que $x^{*}\in \mathbb {E} ^{*}$ est un sous-gradient de $f$ en $x\in \operatorname {dom} \,f$ si l'une des propriétés équivalentes suivantes est vérifiée :

$\forall \,y\in \mathbb {E} ,~f(y)\geqslant f(x)+\langle x^{*},y-x\rangle$ ,
$x$ minimise $y\in \mathbb {E} \mapsto f(y)-\langle x^{*},y\rangle$ ,
$f^{*}(x^{*})+f(x)\leqslant \langle x^{*},x\rangle$ ,
$f^{*}(x^{*})+f(x)=\langle x^{*},x\rangle$ .

L'ensemble des sous-gradients de $f$ en $x$ est appelé le sous-différentiel de $f$ en $x$ ; il est noté

$\partial f(x).$

On dit que $f$ est sous-différentiable en $x$ si $\partial f(x)\neq \varnothing$ . Par convention, $\partial f(x)=\varnothing$ si $x\notin \operatorname {dom} \,f$ .

Annexes

Notes

Voir Clarke (1983).
La caractérisation de l'intériorité relative est peut-être due à Gilbert (2015). La caractérisation de l'unicité peut s'obtenir à partir de résultats plus généraux de Burke et Ferris (1993).
J.-B. Hiriart-Urruty (2013). Bases, outils et principes pour l’analyse variationnelle. Mathématiques et Applications 70. Springer Verlag.
Proposition 6 chez Rockafellar (1976).
Proposition IV.4.2.1 chez Hiriart-Urruty et Lemaréchal (2001).
Théorème 25.1 chez Rockafellar (1970).
Voir Davis (1957) et la section 5.2 chez Borwein et Lewis (2000).

Bibliographie

(en) A. Auslender, M. Teboulle (2003). Asymptotic Cones and Functions in Optimization and Variational Inequalitites. Springer Monographs in Mathematics. Springer, New York.
(en) J. F. Bonnans, A. Shapiro (2000). Perturbation Analysis of Optimization Problems. Springer Verlag, New York.
(en) J.M. Borwein, A.S. Lewis (2000). Convex Analysis and Nonlinear Optimization. Springer, New York.
(fr) H. Brézis (1973). Opérateurs Maximaux Monotones et Semi-groupes de Contractions Dans les Espaces de Hilbert. Mathematics Studies 5. North-Holland, Amsterdam. (ISBN 978-0-7204-2705-9).
(en) J.V. Burke, M.C. Ferris (1993). Weak sharp minima in mathematical programming. SIAM Journal on Control and Optimization, 31, 1340–1359. DOI
(en) C. Davis (1957). All convex invariant functions of Hermitian matrices. Archiv der Mathematik, 8, 26-278.
(en) F.H. Clarke (1983). Optimization and Nonsmooth Analysis. John Wiley & Sons, New York.
(en) J.Ch. Gilbert (2015). On the solution uniqueness characterization in the $\ell _{1}$ norm and polyhedral gauge recovery. Rapport INRIA.
(fr) J.-B. Hiriart-Urruty (1998). Optimisation et Analyse Convexe. Presses Universitaires de France, Paris.
(en) J.-B. Hiriart-Urruty, Cl. Lemaréchal (2001). Fundamentals of Convex Analysis. Springer. (ISBN 978-3-540-42205-1).
(en) A.S. Lewis (1996). Convex analysis on the Hermitian matrices. SIAM Journal on Optimization, 6, 164-177.
(en) R.T. Rockafellar (1970). Convex Analysis. Princeton Mathematics Ser. 28. Princeton University Press, Princeton, New Jersey.
(en) R.T. Rockafellar (1976). Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization, 14, 877–898.
(en) R.E. Showalter (1997). Monotone Operators in Banach Space and Nonlinear Partial Differential Equations. American Mathematical Society. (ISBN 978-0-8218-0500-8).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.