Altitudes et coordonnées géographiques sur les corps célestes
Que ce soit sur Terre ou sur d'autres corps célestes, il est nécessaire de définir un référentiel d'altitude et de coordonnées géographiques afin de pouvoir localiser différents objets (caractéristiques de surface, éléments de structure interne, atmosphériques ou extra-atmosphériques) par rapport à ces corps. Pour chacun de ces corps, des conventions ont donc été établies, qui sont ici détaillées.
Définition
Le groupe de travail de l'UAI sur les coordonnées cartographiques et les éléments de rotation
L'Union astronomique internationale (UAI) a donné au groupe de travail de l'UAI sur les coordonnées cartographiques et les éléments de rotation (en anglais IAU Working Group on Cartographic Coordinates and Rotational Elements, WGCCRE) la responsabilité de définir les éléments de rotation des planètes, des satellites, des astéroïdes (en fait, des planètes mineures en général) et des comètes du système solaire de façon systématique et de faire correspondre leurs coordonnées cartographiques rigoureusement aux éléments de rotation[1].
En pratique, le groupe de travail a accompli cette tâche en publiant un rapport après chaque assemblée générale (triennale) de l'UAI, lequel décrit les modèles recommandés actuels pour les coordonnées cartographiques et les éléments de rotation de tous les corps planétaires pour lesquels une telle connaissance existe, par exemple grâce aux missions spatiales[1].
Les rapports du groupe de travail
- ...
- Rapport ? (1980), faisant suite à l'assemblée générale de l'Union astronomique internationale de 1979et_al.''_1980_2-0">[2]
- ...
- Rapport 11 (2011), faisant suite à l'assemblée générale de l'Union astronomique internationale de 2009[3] ;
- Erratum aux rapports 10 et 11 (2011)[4] ;
- Système de coordonnées pour (4) Vesta (2013)[5] ;
- Pas de rapport 12 à la suite de l'assemblée générale de l'Union astronomique internationale de 2012 ;
- Rapport 13 (2018), faisant suite à l'assemblée générale de l'Union astronomique internationale de 2015[6] ;
- Correction au rapport 13 (2019)[7].
Source des définitions actuelles
Depuis , l'ensemble des définitions en vigueur sont regroupées dans le rapport 13 (Archinal et al. 2018, avec corrections dans Archinal et al. 2019), faisant suite à l'assemblée générale de l'Union astronomique internationale de 2015[6] - [7].
« Règles » générales
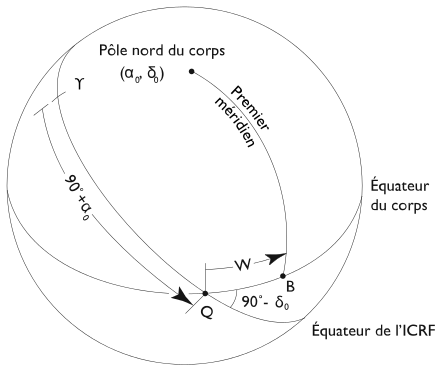
Altitude
Pour les objets sphéroïdaux dont l'aplatissement est négligeable, le niveau de référence des altitudes des altitudes correspond au rayon moyen du corps considéré. Dans les autres cas, si la forme est proche d'un ellipsoïde, un ellipsoïde aplati ou un ellipsoïde triaxial est habituellement utilisé.
Pôles et points cardinaux
En ce qui concerne les objets du système solaire, deux cas sont à distinguer, avec chacun leur convention.
Le premier cas est celui des planètes et de leurs satellites. Pour ces objets, le pôle de référence est le pôle nord, défini comme le pôle de rotation du corps qui se situe du côté nord du plan invariable. La définition de ce pôle est donc indépendante du fait que la rotation du corps soit prograde ou rétrograde. Le pôle sud est alors défini comme le pôle opposé. L'est et l'ouest sont alors définis de façon usuelle, avec l'est 90 degrés à droite du nord. La rotation s'effectue ainsi vers l'est pour les objets en rotation prograde (comme la Terre) mais vers l'ouest pour les objets en rotation rétrograde (comme Vénus).
Le deuxième cas est celui des planètes naines et des petits corps (planètes mineures et comètes) ainsi que de leurs satellites. Depuis 2006, pour ces objets, le pôle de référence est le pôle positif, défini selon la règle de la main droite. Ce pôle est souvent appelé par abus pôle nord, mais il doit être clair qu'il n'est pas défini de la même façon que pour les planètes et leurs satellites. Le pôle opposé est le pôle négatif, par abus appelé pôle sud. L'est et l'ouest sont définis en cohérence avec le fait d'associer le pôle positif au nord, avec pour conséquence le fait que la rotation de ces objets se fait toujours vers l'est. Cette convention a été choisie en raison du fait que les pôles de rotation de ces corps mineurs peuvent avoir une grande précession (par exemple dans le cas de la comète 2P/Encke) et que la rotation de certains est dans un état excité (par exemple les comètes 1P/Halley et 103P/Hartley et l'astéroïde (4179) Toutatis)[6].
Latitude
Pour les objets ayant une rotation « stable » (comprendre : dont l'axe ne varie pas de façon chaotique à relativement courte échelle de temps), la latitude est définie à partir de l'équateur, qui par définition est le plan médian orthogonal à l'axe de rotation. Le pôle nord a alors par définition une latitude de +90˚ (ou 90˚ Nord) et le pôle sud une latitude de -90˚ (ou 90˚ Sud).
Objet en rotation synchrone
Pour un objet A dont la rotation est synchrone avec sa révolution autour d'un objet B, la longitude zéro de A est définie par le point moyen de A faisant face à B. Par exemple, la Lune montrant (à l'excentricité de son orbite près) toujours la même face à la Terre, la longitude zéro de la Lune relie les pôles de cette dernière en passant par le centre de cette face.
Objet dans une autre résonance spin-orbite
Pour un objet en résonance spin-orbite dont l'excentricité orbitale n'est pas nulle, le méridien origine peut être choisi comme un des méridiens (en nombre fini) qui sont au point subsolaire lors des passages au périhélie. C'est en particulier ce qui a été choisi pour Mercure.
Autres objets
Pour ces objets, un point arbitraire sert de référence pour définir la longitude 0. Par exemple, sur Terre, il s'agit de l'observatoire de Greenwich, via lequel le méridien origine est défini comme étant le méridien de Greenwich.
Dans le système solaire
Soleil
La localisation d'une caractéristique spécifique sur le Soleil (par exemple, une tache solaire) est compliquée par le fait qu'il y a une inclinaison de 7,25 degrés entre le plan écliptique et le plan de l'équateur solaire ainsi qu'une véritable oscillation de l'axe de rotation solaire. (le pôle nord solaire et le pôle nord céleste ne sont alignés que deux fois par an). Par conséquent, pour spécifier un emplacement sur la surface solaire, trois coordonnées (P, B et L) sont nécessaires pour définir une grille. Les valeurs quotidiennes des coordonnées en temps universel coordonné (UTC) sont répertoriées dans The Astronomical Almanac, publié chaque année par l'US Naval Observatory.
Les termes utilisés pour faire référence aux coordonnées sont définis comme suit :
- angle P : angle de position entre le pôle nord géocentrique et le pôle nord de la rotation solaire mesuré vers l'est à partir du nord géocentrique. L'intervalle de valeurs de P est ±26,3 degrés.
- B0 : latitude héliographique du point central du disque solaire, également appelé l'angle B. La plage de Bo est de ±7,23 degrés, corrigeant l'inclinaison de l'écliptique par rapport au plan solaire équatorial.
Exemple : Si (P ; B0) = (-26,21° ; -6,54°), la latitude héliographique du point central du disque solaire est de -6,54 degrés (le pôle de rotation nord n'est pas visible) et l'angle entre la projection sur le disque du pôle nord géocentrique et le pôle de rotation nord solaire est de 26,21 degrés à l'ouest.
- L0 : longitude héliographique du point central du disque solaire. La valeur de longitude est déterminée par référence à un système de longitudes fixes tournant sur le Soleil à un taux de 13,2 degrés par jour (le taux de rotation moyen observé à partir des transits méridiens centraux des taches solaires). Le méridien de référence sur le Soleil est défini comme étant le méridien qui a traversé le nœud ascendant de l'équateur du Soleil le à 12 h 0 UTC et est calculé pour le jour actuel en supposant une période de rotation sidérale uniforme de 25,38 jours.
Une fois P, B0 et L0 connus, la latitude, la distance du méridien central et la longitude d'une entité solaire spécifique peuvent être déterminées comme suit :
- latitude : distance du méridien central (DMC ; CMD en anglais pour central meridian distance): distance angulaire en longitude solaire mesurée à partir du méridien central. Cette position est relative à la vue depuis la Terre et changera au fur et à mesure que le Soleil tourne. Par conséquent, cette coordonnée ne doit pas être confondue avec des positions héliographiques qui sont fixes par rapport à la surface solaire.
- longitude : distance angulaire depuis un méridien de référence (0 degrés de longitude héliographique), mesurée d'est en ouest (0 degrés à 360 degrés) le long l'équateur du Soleil. Il est calculé en combinant la DMC avec la longitude du méridien central au moment de l'observation, en interpolant entre les valeurs des éphémérides (pour 0 h 0 UT) en utilisant le taux synodique de rotation solaire (27,2753 jours, 13,2 degrés par jour)[8].
Mercure

Mercure ayant une rotation très lente sur elle-même, son aplatissement[N 1] est très faible, ce qui permet d'utiliser comme niveau zéro des altitudes le rayon moyen de la planète par rapport à son centre. Le rayon recommandé dans le rapport du WGCCRE paru en 2018 (Archinal et al. 2018) est 2 439,4 ± 0,1 kilomètreset_al.''_2018_10-0">[9]. La moyenne quadratique des déviations à cette boule est de 1 km, avec un maximum d'altitude à 4,6 km et un minimum à −2,5 kmet_al.''_2018_10-1">[9]. Le meilleur ellipsoïde triaxial donne des dimensions de (2 440,54 × 2 439,28 × 2 438,26) km[N 2], avec une incertitude de 0,04 km sur la longueur de chacun des trois demi-axeset_al.''_2018_10-2">[9].
Concernant les coordonnées à la surface de la planète, ce n'est que depuis 1970 que celles-ci sont correctement définies. En effet, avant 1965, les cartes réalisées à partir des observations faites sur Terre étaient établies alors qu'on pensait, comme Giovanni Schiaparelli l'avait affirmé en 1889[10], que la période de rotation de Mercure sur elle-même était la même que sa période de révolution autour du Soleil. C'était donc la face supposée toujours illuminée qui était cartographiée[11]. La référence 0 de longitude passait alors au centre de cette face.
 Carte de Giovanni Schiaparelli (avant 1911).
Carte de Giovanni Schiaparelli (avant 1911). Carte de Percival Lowell (1896).
Carte de Percival Lowell (1896). Carte d'Eugène Antoniadi (1934).
Carte d'Eugène Antoniadi (1934).
Cependant, en 1965, Gordon Pettengill et Rolf Dyce[12], de l'université Cornell, obtiennent une mesure fiable de la période de rotation de Mercure en utilisant le radiotélescope d'Arecibo[10]. Contrairement à la prédiction faite par Schiaparelli, Mercure n'est pas en rotation synchrone autour du Soleil mais est en résonance spin-orbite 3:2[10]. L'Union astronomique internationale redéfinit alors, en 1970, le méridien 0° de Mercure comme étant le méridien solaire au premier périhélie après le . Les longitudes sont mesurées de 0° à 360° en allant vers l'ouest.
Le système de coordonnées utilisé par Mariner 10, première sonde spatiale à explorer Mercure, se fonde sur le méridien de longitude 20˚ ouest qui coupe le petit cratère Hun Kal (1,5 km de diamètre) en son centre[13] - [14] (« Hun Kal » signifie « 20 » en maya), ce qui donne une légère erreur de moins de 0,5° par rapport au méridien 0° défini par l'UAI. Le cratère Hun Kal est depuis lors en quelque sorte le Greenwich de Mercure puisque c'est cette référence qui est toujours utilisée aujourd'hui. Le choix de Hun Kal s'explique par le fait que le « vrai » méridien origine (0˚ de longitude) était à l'ombre lorsque Mariner 10 photographia la région, cachant toute caractéristique proche de la longitude 0° qui aurait pu servir de référence. Pour définir la latitude, l'axe de rotation de Mercure était supposé normal (perpendiculaire) au plan orbital de la planète, ou de façon équivalente, l'équateur était supposé se trouver dans le plan de l'orbite de Mercure[13] — en réalité, l'inclinaison de l'axe de la planète n'est pas strictement nulle mais néanmoins très faible, (0,035 2 ± 0,001 7)° [soit (2,112 ± 0,102)'], ce qui correspond à un écart maximal entre les définitions des parallèles de 1,50 ± 0,07 kilomètre à la surface de la planète.
Le rapport du WGCCRE paru en 2018et_al.''_2018_10-3">[9] indique que le méridien de longitude 20˚ est défini par le cratère Hun Kal et donne comme paramètres :
- α0 = (281,0103 − 0,0328 T)°
- δ0 = (61,4155 − 0,0049 T)°
- W = (329,5988 ± 0,0037 + 6,138 510 8 d + 0,010 672 57 sin M1 − 0,001 123 09 sin M2 − 0,000 110 40 sin M3 − 0,000 025 39 sin M4 − 0,000 005 71 sin M5)°
où
- M1 = (174,791 085 7 + 4,092 335 d)°
- M2 = (349,582 171 4 + 8,184 670 d)°
- M3 = (164,373 257 1 + 12,277 005 d)°
- M4 = (339,164 342 9 + 16,369 340 d)°
- M5 = (153,955 428 6 + 20,461 675 d)°
où d et T sont les intervalles, respectivement en jours (86400 secondes) et en siècles juliens (36525 jours), depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
 Le cratère Hun Kal, indiqué par une flèche.
Le cratère Hun Kal, indiqué par une flèche. Image montrant les alentours de Hun Kal, lequel est presque invisible, minuscule proche du centre.
Image montrant les alentours de Hun Kal, lequel est presque invisible, minuscule proche du centre. Photo de Mercure prise par Mariner 10.
Photo de Mercure prise par Mariner 10. L'autre face de Mercure, non photographiée par Mariner 10, ici prise par MESSENGER.
L'autre face de Mercure, non photographiée par Mariner 10, ici prise par MESSENGER.
Vénus

Vénus ayant une rotation très lente sur elle-même (plus lente encore que Mercure), son aplatissement[N 1] est très faible, ce qui permet d'utiliser comme niveau zéro des altitudes le rayon moyen de la planète par rapport à son centre. Le rayon recommandé dans le rapport du WGCCRE paru en 2018 (Archinal et al. 2018) est 6 051,8 ± 1,0 kilomètreset_al.''_2018_10-4">[9]. La moyenne quadratique des déviations à l'ellipsoïde est de 1 km, avec un maximum d'altitude à 11 km et un minimum à −2 kmet_al.''_2018_10-5">[9].
Les longitudes sur Vénus sont mesurées en allant vers l'est depuis son méridien origine. À l'origine, ce premier méridien passait par la tâche brillante pour les radars située au centre de la caractéristique ovale Eve, située au sud d'Alpha Regio[15]. Après que les missions Venera furent achevées, le premier méridien fut redéfini comme passant par le pic central dans le cratère Ariadne[16] - [17].
Le rapport du WGCCRE paru en 2018et_al.''_2018_10-6">[9] indique que le méridien de longitude 0˚ est défini par le cratère Ariadne et donne comme paramètres :
- α0 = 272,76°
- δ0 = 67,16°
- W = (160,20 - 1,481 368 8 d)°
où d est l'intervalle, en jours (86400 secondes), depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Terre
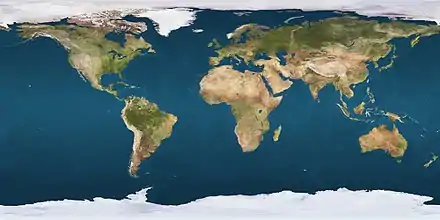
 Latitude et longitude sur la Terre.
Latitude et longitude sur la Terre.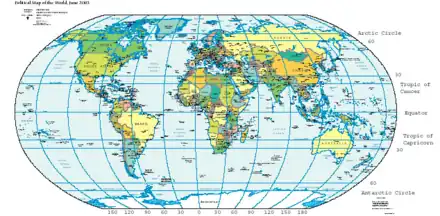 Carte du monde montrant la latitude et la longitude, suivant une projection de type Eckert VI ; version PDF large (pdf, 1,8 MB). La latitude est marquée suivant l'axe vertical, mais la longitude n'est pas mesurable directement par une mesure horizontale, car cette distance est réduite aux pôles, pour mieux correspondre aux distances terrestres réelles, sans pouvoir toutefois donner des distances exactes. Une telle déformation des distances (et des formes et angles) est inévitable avec n'importe quelle projection sur une carte plane.
Carte du monde montrant la latitude et la longitude, suivant une projection de type Eckert VI ; version PDF large (pdf, 1,8 MB). La latitude est marquée suivant l'axe vertical, mais la longitude n'est pas mesurable directement par une mesure horizontale, car cette distance est réduite aux pôles, pour mieux correspondre aux distances terrestres réelles, sans pouvoir toutefois donner des distances exactes. Une telle déformation des distances (et des formes et angles) est inévitable avec n'importe quelle projection sur une carte plane.
Lune
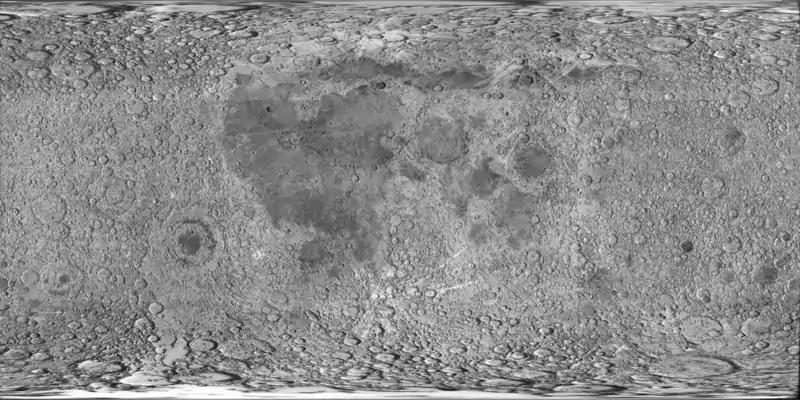
Tout point sur la Lune peut être spécifié par deux valeurs numériques, analogues de la latitude et la longitude terrestres. La longitude donne la position à l'est ou à l'ouest du premier méridien lunaire qui passe par le point faisant directement face à la Terre. La latitude donne la position au nord ou au sud de l'équateur lunaire. Ces deux coordonnées sont exprimés en degrés.
En pratique, le point de référence est le cratère Mösting A, un petit cratère en forme de bol, situé par 3,212, −5,211.
Sur la Lune, on mesure les altitudes des sommets relativement à une distance donnée à son centre. Dans les années 1990, la mission Clementine a publié des valeurs basées sur le chiffre de 1 737 400 mètres. Cette valeur est aussi celle recommandée par Archinal et al. (2018)et_al.''_2018_10-7">[9]. La moyenne quadratique des déviations à cette sphère est de 2,5 km, avec un maximum d'altitude à 7,5 km et un minimum à −5,6 kmet_al.''_2018_10-8">[9].
Mars

Sur Mars, en l'absence d'océan, l'origine des altitudes a été fixée de façon arbitraire : c'est l'altitude ayant une pression atmosphérique moyenne de 610 pascals. Cette pression a été choisie parce qu'elle est proche à la pression du point triple de l'eau (273,16 K et 611,73 Pa) et que le niveau ainsi défini est proche du niveau moyen de la surface martienne (sur Terre, c'est la pression atmosphérique à 35 kilomètres d'altitude). Cependant, la pression peut fortement varier à la surface de Mars et donc cette définition ne permet pas de définir précisément un niveau zéro. Le niveau zéro actuel, tel qu'indiqué par le rapport du WGCCRE paru en 2018, est défini par un ellipsoïde aplati de rayon équatorial (3 396,19 ± 0,1) km et de rayon polaire (3 376,20 ± 0,1) km. La moyenne quadratique des déviations à l'ellipsoïde est de 3,0 km, avec un maximum d'altitude à (22,64 ± 0,1) km (le mont Olympe) et un minimum à (−7,55 ± 0,1) kmet_al.''_2018_10-9">[9].
Le méridien 0 de Mars a été défini en 1830 par les astronomes allemands Wilhelm Beer et Johann Heinrich von Mädler en se fondant sur une petite formation circulaire proche de l'équateur dont ils se servirent pour déterminer la période de rotation de Mars. Cette formation circulaire fut reprise par la suite en 1877 par l'astronome italien Giovanni Schiaparelli qui en fit le méridien 0 de ses longitudes. L'astronome français Camille Flammarion la baptisa Sinus Meridiani (« Baie du méridien »), d'où provient le toponyme actuel Meridiani Planum désignant cette région. Le cratère Airy fut choisi dans cette région pour matérialiser plus précisément le méridien 0 et, à la suite de la cartographie de la surface de Mars obtenue en 1972 par la sonde Mariner 9 avec une résolution moyenne de l'ordre du kilomètre, le centre du petit cratère Airy-0, situé à l'intérieur du cratère Airy et large de 500 m seulement, a été choisi pour positionner le méridien 0 sur Mars[18]. Finalement, c'est l'atterrisseur Viking 1 qui sert de référence en ayant une longitude officiellement assignée de 47,951 37 degrés ouestet_al.''_2018_10-10">[9].
Le rapport du WGCCRE paru en 2018et_al.''_2018_10-11">[9] indique que la longitude de l'atterrisseur Viking 1 est définie comme étant 47,951 37 degrés ouest, ce qui maintient le méridien 0° à travers le cratère Airy-0, et donne comme paramètres :
- α0 = (317,269 202 − 0,109 275 47 T + 0,000 068 sin(198,991 226 + 19 139,481 998 5 T) + 0,000 238 sin(226,292 679 + 38 280,851 128 1 T) + 0,000 052 sin(249,663 391 + 57 420,725 159 3 T) + 0,000 009 sin(266,183 510 + 76 560,636 795 0 T) + 0,419 057 sin(79,398 797 + 0,504 261 5 T))°
- δ0 = (54,432 516 − 0,058 271 05T + 0,000 051 cos(122,433 576 + 19 139,940 747 6 T) + 0,000 141 cos(43,058 401 + 38 280,875 327 2 T) + 0,000 031 cos(57,663 379 + 57 420,751 720 5 T) + 0,000 005 cos(79,476 401 + 76 560,649 500 4 T) + 1,591 274 cos(166,325 722 + 0,504 261 5 T))°
- W = (176,049 863 + 350,891 982 443 297 d + 0,000 145 sin(129,071 773 + 19 140,032 824 4 T) + 0,000 157 sin(36,352 167 + 38 281,047 359 1 T) + 0,000 040 sin(56,668 646 + 57 420,929 536 0 T) + 0,000 001 sin(67,364 003 + 76 560,255 221 5 T) + 0,000 001 sin(104,792 680 + 95 700,438 757 8 T) + 0,584 542 sin(95,391 654 + 0,504 261 5 T))°
où d et T sont les intervalles, respectivement en jours (86400 secondes) et en siècles juliens (36525 jours), depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
En ce qui concerne les latitudes, deux systèmes sont actuellement en vigueur, bien que le second tende à se généraliser — aussi bien au sein de la NASA que de l'ESA — au détriment du premier depuis le début du siècle :
- Les latitudes ont initialement été déterminée dans un cadre planétographique consistant à les calculer directement à partir des distances extrapolées sur les clichés obtenus de la surface de la planète par rapport à un maillage de coordonnées projeté sur cette surface. Dans ce système, utilisé par le programme Viking, les longitudes sont exprimées de 0 à 360° W, c'est-à-dire en croissant vers l'ouest.
- Depuis le début du siècle, le système planétographique tend à être remplacé par le système planétocentrique, bien que les deux aient été validés par l'UAI en 2000 ; dans ce système, les latitudes sont calculées à partir de l'angle formé par un point de la surface avec le plan équatorial de Mars, tandis que les longitudes sont exprimées de 0 à 360° E, c'est-à-dire en croissant vers l'est.
Phobos (Mars I)
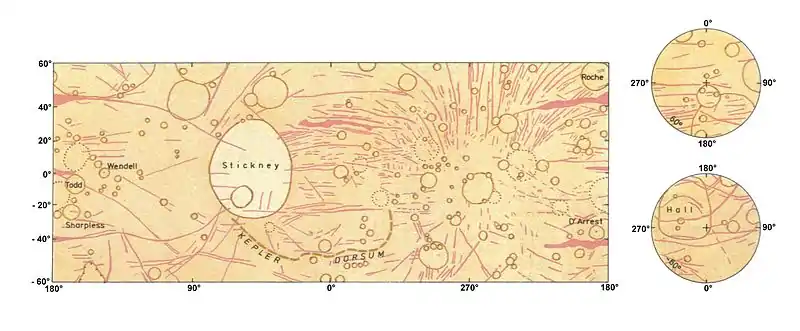
Le méridien de référence de Phobos est le méridien centré sur l'hémisphère faisant face à Mars, Phobos étant en rotation synchrone avec cette planète.
Phobos a un rayon moyen de (11,08 ± 0,04) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 13,0 km, un rayon équatorial le long de l'orbite de 11,4 km et un rayon polaire de 9,1 km. La moyenne quadratique des déviations à l'ellipsoïde est de 0,5 kmet_al.''_2018_10-12">[9].
Déimos (Mars II)
Le méridien de référence de Déimos est le méridien centré sur l'hémisphère faisant face à Mars, Déimos étant en rotation synchrone avec cette planète.
Déimos a un rayon moyen de (6,2 ± 0,25) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 7,8 km, un rayon équatorial le long de l'orbite de 6,0 km et un rayon polaire de 5,1 km. La moyenne quadratique des déviations à l'ellipsoïde est de 0,2 kmet_al.''_2018_10-13">[9].
Jupiter

Le niveau zéro des altitudes correspond à là où la pression vaut un bar. L'ellipsoïde aplati correspondant a un rayon équatorial de (71 492 ± 4) km et un rayon polaire de (66 854 ± 10) km. La moyenne quadratique des déviations à l'ellipsoïde est de 62,1 km, avec un maximum d'altitude à 31 km et un minimum à −102 kmet_al.''_2018_10-14">[9].
Métis (Jupiter XVI)
Métis a un rayon moyen de (21,5 ± 4) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 30 km, un rayon équatorial le long de l'orbite de 20 km et un rayon polaire de 17 kmet_al.''_2018_10-15">[9].
Adrastée (Jupiter XV)
Adrastée a un rayon moyen de (8,2 ± 4) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 10 km, un rayon équatorial le long de l'orbite de 8 km et un rayon polaire de 7 kmet_al.''_2018_10-16">[9].
Amalthée (Jupiter V)
Amalthée a un rayon moyen de (83,5 ± 3) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 125 km, un rayon équatorial le long de l'orbite de 73 km et un rayon polaire de 64 km. La moyenne quadratique des déviations à l'ellipsoïde est de 3,2 kmet_al.''_2018_10-17">[9].
Thébé (Jupiter XIV)
Thébé a un rayon moyen de (49,3 ± 4) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 58 km, un rayon équatorial le long de l'orbite de 49 km et un rayon polaire de 42 kmet_al.''_2018_10-18">[9].
Io (Jupiter I)

Io a un rayon moyen de 1 821,49 km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 1 829,4 km, un rayon équatorial le long de l'orbite de 1 819,4 km et un rayon polaire de 1 815,7 km. Le maximum d'altitude est de 13 km et le minimum de −3 kmet_al.''_2018_10-19">[9].
Io est en rotation synchrone avec Jupiter. Le méridien de référence de Io est le méridien centré sur l'hémisphère faisant face à Jupiter, car on suppose que les caractéristiques de surface de Io ne dureront pas assez longtemps pour servir de référence à long termeet_al.''_2018_10-20">[9].
Europe (Jupiter II)
Europe a un rayon moyen de (1 560,8 ± 0,3) km. L'ellipsoïde triaxial correspondant le mieux au satellite a un rayon équatorial sous-planétaire de 1 562,6 km, un rayon équatorial le long de l'orbite de 1 560,3 km et un rayon polaire de 1 559,5 km. La moyenne quadratique des déviations à l'ellipsoïde est de 0,32 kmet_al.''_2018_10-21">[9].
Le méridien de référence d'Europe est défini en fixant à 182° la longitude du cratère Cilixet_al.''_2018_10-22">[9].
Ganymède (Jupiter III)

Ganymède est sphérique, de rayon moyen de (2 631,2 ± 1,7) kmet_al.''_2018_10-23">[9].
Le méridien de référence de Ganymède est défini en fixant à 128° la longitude du cratère Anatet_al.''_2018_10-24">[9].
Callisto (Jupiter IV)
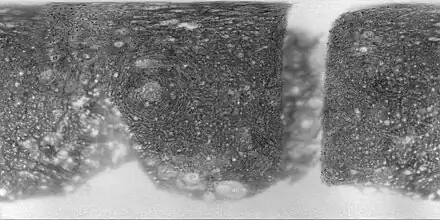
Callisto est sphérique, de rayon moyen de (2 410,3 ± 1,5) km. La moyenne quadratique des déviations à cette sphère est de 0,6 kmet_al.''_2018_10-25">[9].
Le méridien de référence de Callisto est défini en fixant à 326° la longitude du cratère Sagaet_al.''_2018_10-26">[9].
Saturne
Le niveau zéro des altitudes correspond à là où la pression vaut un bar. L'ellipsoïde aplati correspondant a un rayon équatorial de (60 268 ± 4) km et un rayon polaire de (54 364 ± 10) km. La moyenne quadratique des déviations à l'ellipsoïde est de 102,9 km, avec un maximum d'altitude à 8 km et un minimum à −205 kmet_al.''_2018_10-34">[9].
Mimas (Saturne I)
_map.jpg.webp)
Le méridien de référence de Mimas est défini en fixant à 162° la longitude du cratère Palomideset_al.''_2018_10-35">[9].
Encelade (Saturne II)

Le méridien de référence d'Encelade est défini en fixant à 5° la longitude du cratère Salihet_al.''_2018_10-36">[9].
Téthys (Saturne III)

Le méridien de référence de Téthys est défini en fixant à 299° la longitude du cratère Areteet_al.''_2018_10-37">[9].
Dioné (Saturne IV)
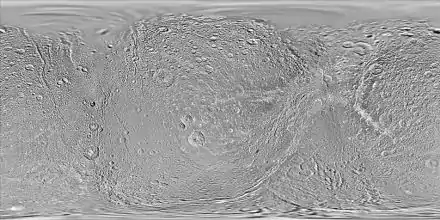
Le méridien de référence de Dioné est défini en fixant à 63° la longitude du cratère Palinureet_al.''_2018_10-38">[9].
Rhéa (Saturne V)

Le méridien de référence de Rhéa est défini en fixant à 340° la longitude du cratère Toreet_al.''_2018_10-39">[9].
Titan (Saturne VI)
Étant donné que la rotation de Titan est synchrone avec sa révolution autour de Saturne, le satellite présente toujours la même face à la planète, à la faible excentricité de son orbite près. Le méridien origine (longitude 0°) de Titan est pour cette raison défini comme étant le méridien passant par la position moyenne du centre de cette face. La longitude va ensuite en croissant vers l'ouest, de 0° à 360° ouest.

Japet (Saturne VIII)

Le méridien de référence de Japet est défini en fixant à 276° la longitude du cratère Almericet_al.''_2018_10-40">[9].
Uranus
Le niveau zéro des altitudes correspond à là où la pression vaut un bar. L'ellipsoïde aplati correspondant a un rayon équatorial de (25 559 ± 4) km et un rayon polaire de (24 973 ± 20) km. La moyenne quadratique des déviations à l'ellipsoïde est de 16,8 km, avec un maximum d'altitude à 28 km et un minimum à 0 kmet_al.''_2018_10-41">[9].
Miranda (Uranus V)
Le méridien de référence de Miranda est le méridien centré sur l'hémisphère faisant face à Uranus, Miranda étant en rotation synchrone avec cette planète[19].
Ariel (Uranus I)
Le méridien de référence d'Ariel est le méridien centré sur l'hémisphère faisant face à Uranus, Ariel étant en rotation synchrone avec cette planète[20].
Umbriel (Uranus II)
Le méridien de référence d'Umbriel est le méridien centré sur l'hémisphère faisant face à Uranus, Umbriel étant en rotation synchrone avec cette planète[21].
Titania (Uranus III)
Le méridien de référence de Titania est le méridien centré sur l'hémisphère faisant face à Uranus, Titania étant en rotation synchrone avec cette planète[21].
Obéron (Uranus IV)
Le méridien de référence d'Obéron est le méridien centré sur l'hémisphère faisant face à Uranus, Obéron étant en rotation synchrone avec cette planète[21].
Neptune
Le niveau zéro des altitudes correspond à là où la pression vaut un bar. L'ellipsoïde aplati correspondant a un rayon équatorial de (24 764 ± 15) km et un rayon polaire de (24 341 ± 30) km. La moyenne quadratique des déviations à l'ellipsoïde est de 8 km, avec un maximum d'altitude à 14 km et un minimum à 0 kmet_al.''_2018_10-42">[9].
Triton (Neptune I)
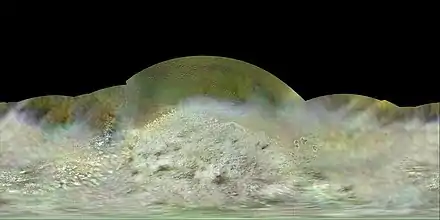
Le méridien de référence d'Triton est le méridien centré sur l'hémisphère faisant face à Neptune, Triton étant en rotation synchrone avec cette planète[22].
Cérès

Le système de coordonnées actuel sur Cérès est décrit par C. Raymond, du Jet Propulsion Laboratory, et T. Roatsch, du DLR, dans un document du [23].
Le petit cratère Kait, situé à 2,1 degrés de latitude sud et mesurant environ 800 mètres de diamètre, définit la longitude zéro[23].
Le système de coordonnées de Cérès défini par Raymond et Roatsch correspond aux équations suivantes[23] :
- α0 = (291,418 ± 0,03)°, δ0 = (66,764 ± 0,03)°, W = (170,650 + [952,153 2 ± 0,000 03] d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Le système de coordonnées de Cérès défini par Park et al. en 2016 correspond aux équations suivanteset_al.''_2016_26-0">[24] :
- α0 = (291,421 ± 0,007)°, δ0 = (66,758 ± 0,002)°, W = (170,65 + [952,153 2 ± 0,000 1] d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Le précédent système de coordonnées, utilisé dans Archinal et al. (2011), était fixé par rapport à une caractéristique brillante observée dans les données du télescope spatial Hubble (Thomas et al., 2005) et nommée "Feature #1" dans Li et al. (2006). Cette caractéristique, centrée à 1°E, 12°N sur leur carte (figure 5 de Li et al., 2006), est bien visible dans les filtres F330W et F220W et beaucoup plus petite et "muted" dans le filtre F555W. Un cratère brillant mesurant environ 32 kilomètres, nommé Haulani, est observé dans la région de Feature #1, entouré par un dépôt d'éjectas généralement plus brillant qui définissent ensemble une région de plus haut albédo. Cependant, l'équipe de Dawn n'a pas pu identifier avec suffisamment de confiance ou de précision la localisation de Haulani par rapport à Feature #1. L'équipe de Dawn a donc choisi un petit cratère situé près de Haulani, à savoir Kait, d'environ 800 mètres de diamètre, pour définir le premier méridien de Cérès. La localisation de ce cratère est à l'intérieur de l'enveloppe de la grande caractéristique identifiée dans les données de Hubble à laquelle le système précédent était fixé. Lorsque les paramètres de rotation seront plus précis, W0 sera ajusté de telle sorte que Kait reste à 0 degré de longitude[23].
Pluton
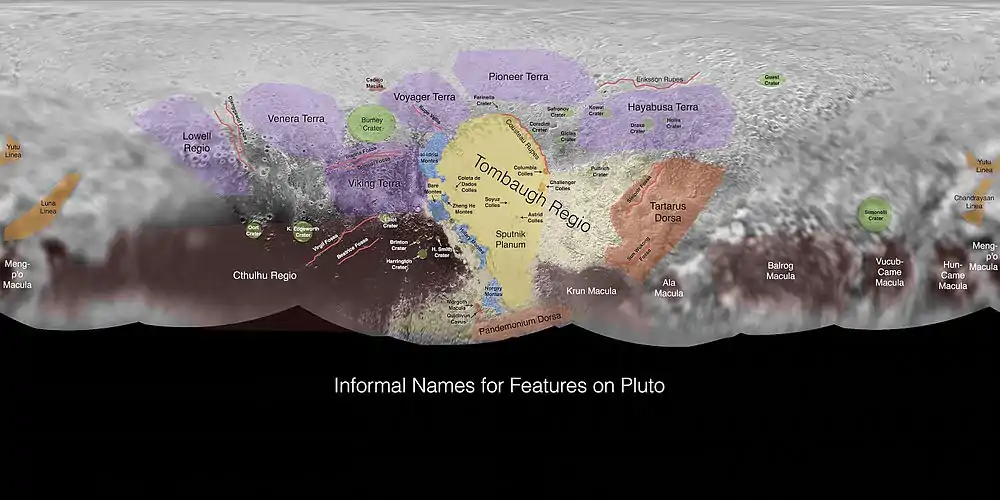
Le méridien de référence de Pluton est le méridien centré sur l'hémisphère faisant face à Charon[25]. En effet, Pluton et Charon étant en rotation synchrone et se montrant l'un à l'autre toujours la même face, le méridien origine ainsi défini est fixe sur la surface de Pluton.
Charon
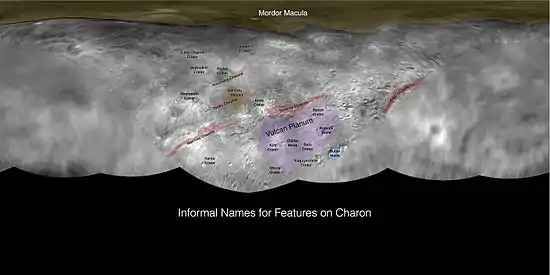
Le méridien de référence de Charon est le méridien centré sur l'hémisphère faisant face à Pluton. En effet, Pluton et Charon étant en rotation synchrone et se montrant l'un à l'autre toujours la même face, le méridien origine ainsi défini est fixe sur la surface de Charon.
Ainsi, les méridiens zéro de Pluton et de Charon se font toujours face.
(2) Pallas
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (2) Pallas le système de coordonnées défini par les équations suivantes :
- α0 = 33°, δ0 = -3°, W = (38 + 1 105,803 6 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à définir le premier méridien de Pallas par la direction (x positifs) du long axe du modèle de forme de Carry et al. (2010a).
(4) Vesta

La région sombre connue informellement sous le nom de région Olbers a en premier été identifiée et définie comme la localisation du premier méridien par Thomas et al. en 1997. Cette zone est facilement identifiée sur les images de la sonde spatiale Dawn comme une zone de faible albédo (c'est-à-dire sombre) qui consiste principalement en une dépression topographique dégradée.
Depuis , le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (4) Vesta le système de coordonnées défini par les équations suivantes :
- α0 = (309,031 ± 0,01)°, δ0 = (42,235 ± 0,01)°, W = (285,39 + 1 617,332 942 8 d)°
où d est l'intervalle, en jours (86400 secondes), depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à définir le premier méridien de Vesta en attribuant une longitude positive de 146° au cratère Claudia. Cette définition, qui suit les recommandations de l'UAI et du WGCCRE et les pratiques passées, conserve le fait que le premier méridien de Vesta passe à travers la région Olbers. Il est recommandé que ce système soit connu comme le « système de coordonnées de l'UAI pour (4) Vesta », auquel l'année de publication de l'annonce (2013) doit être ajoutée s'il est nécessaire de le distinguer de systèmes antérieurs ou postérieurs recommandés pour Vesta.
Cette définition est confirmée dans le rapport du WGCCRE paru en 2018et_al.''_2018_10-43">[9].
(21) Lutèce
Le rapport du WGCCRE paru en 2018et_al.''_2018_10-44">[9] indique, comme le précédent, que le méridien 0 degré de (21) Lutèce a (jusqu'à présent) été défini arbitrairement à partir des informations de la courbe de lumière et donne comme paramètres :
- α0 = (52 ± 5)°, δ0 = (12 ± 5)°, W = (94 + 1 057,751 5 d)°
où d est l'intervalle, en jours (86 400 secondes), depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
(243) Ida
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (243) Ida le système de coordonnées défini par les équations suivantes :
- α0 = 168,76°, δ0 = -2,88°, W = (265,95 + 1 864,628 007 0 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à la définition du premier méridien par le cratère Afon.
(433) Éros
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (433) Éros le système de coordonnées défini par les équations suivantes :
- α0 = (11,35 ± 0,02)°, δ0 = (17,22 ± 0,02)°, W = (326,07 + 1 639,388 647 45 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à la définition du premier méridien par un cratère anonyme.
(511) Davida
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (2) Pallas le système de coordonnées défini par les équations suivantes :
- α0 = 297°, δ0 = 5°, W = (268,1 + 1 684,419 354 9 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à définir le premier méridien par la direction du long axe qui pointait vers la Terre le à 7 h 50 temps universel (« 7.83 UT » dans l'original) (Conrad et al. 2007). Les valeurs apparaissant dans Conrad et al. 2007 ont été remplacées par celles au-dessus, qui apparaissent dans une publication des mêmes auteurs qui était en préparation lors de la publication du rapport de 2009.
(951) Gaspra
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (2) Pallas le système de coordonnées défini par les équations suivantes :
- α0 = 9,47°, δ0 = 26,70°, W = (83,67 + 1 226,911 485 0 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à définir le premier méridien par le cratère Charax.
(2867) Šteins
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (2) Pallas le système de coordonnées défini par les équations suivantes :
- α0 = 90°, δ0 = -62°, W = (93,94 + 1 428,852 332 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à définir le premier méridien par une caractéristique pas encore formellement nommée, mais baptisée le cratère Spinel par Jorda et al. (2010).
(11351) Leucos
Dans leur article de 2020, Stefano Mattola et ses collaborateur ont déterminé pour l'astéroïde (11351) Leucos une période de rotation de 445,683 ± 0,007 heures et le système de coordonnées défini par les équations suivantes :
- α0 = 248°, δ0 = +58° (± 3° autour de ce point), W = (60,014 + (19,385 96 ± 0,000 30) d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Ceci correspond à définir le premier méridien par l'axe X de l'astéroïde, défini par les auteurs comme celui qui coïncide avec la projection de l'axe principal de plus petite inertie sur le plan XY, plan lui-même défini comme étant celui qui passe par le centre de masse et est perpendiculaire à l'axe de rotation (axe Z)[26].
(25143) Itokawa
Dans son rapport de 2009, le groupe de travail de l'Union astronomique internationale sur les coordonnées cartographiques et les éléments de rotation recommande pour l'astéroïde (25143) Itokawa le système de coordonnées défini par les équations suivantes :
- α0 = 90,53°, δ0 = -66,30°, W = (0 + 712,143 d)°
où d est l'intervalle, en jours, depuis l'époque standard, c'est-à-dire J2000.0 = JD2451545.0, autrement dit le à 12 h TDB.
Seul le taux de rotation étant disponible, le méridien origine est actuellement arbitrairement défini avec W0 = 0°.
(101955) Bénou
Sur (101955) Bénou, le méridien origine est défini par un rocher de 30 mètres de large[27] nommé Simurgh Saxum[28].
(162173) Ryugu
Sur (162173) Ryugu, le méridien origine est défini par Catafo Saxum[29].
67P/Tchourioumov-Guérassimenko
Étant donné la forme de 67P/Tchourioumov-Guérassimenko, comète constituée d'un gros lobe, d'un plus petit lobe et d'un « cou » reliant ces deux lobes (voir photo dans la galerie), la définition des coordonnées semble beaucoup plus difficile. Néanmoins, à partir d'un modèle réaliste de la forme de la comète réalisé à partir des clichés de la sonde Rosetta, les équipes de cette mission ont pu définir un système de coordonnées sur la comète[30].
Comme pour tout corps, la latitude est définie par rapport à l'équateur de l'objet[30], c'est-à-dire le plan médian orthogonal à l'axe de rotation (axe nord-sud) de la comète[30]. Cet axe de rotation se trouve près de là où le « cou » de la comète rejoint le lobe principal[30]. Classiquement, le pôle nord et le pôle sud correspondent à l'intersection de cet axe de rotation avec la surface de la comète[30].
La longitude est pour sa part définie comme suit : l'extrémité du lobe le plus important est à la longitude 0˚ et l'extrémité du lobe secondaire est à 180˚[30].
Une animation montrant la comète en rotation avec indication des coordonnées est disponible ici[30].
 La comète 67P/Tchourioumov-Guérassimenko photographiée par la caméra NAVCAM de Rosetta. Le lobe principal est visible à gauche, le plus petit lobe est visible à droite, et le cou reliant les deux au centre.
La comète 67P/Tchourioumov-Guérassimenko photographiée par la caméra NAVCAM de Rosetta. Le lobe principal est visible à gauche, le plus petit lobe est visible à droite, et le cou reliant les deux au centre. « Tchouri » le . Le pôle nord de la comète est situé approximativement au centre à droite, là où le cou de la comète rejoint le lobe principal. Le méridien origine passe par les pôles et la partie extrémale du lobe principal (vers le bas à gauche).
« Tchouri » le . Le pôle nord de la comète est situé approximativement au centre à droite, là où le cou de la comète rejoint le lobe principal. Le méridien origine passe par les pôles et la partie extrémale du lobe principal (vers le bas à gauche).
81P/Wild (Wild 2)
En dehors du système solaire
Exoplanètes
Pour les exoplanètes que l'on pense être en rotation synchrone, le méridien de référence (longitude 0°) passe par le point substellaire moyen. Cette règle générale est analogue à celle utilisée pour les satellites en rotation synchrone autour de leur planète dans le système solaire.
Parmi les exoplanètes dans ce cas qui ont été cartographiées, nous pouvons citer :
- HD 189733 b[31]
- 55 Cancri eet_al.''_2016Figure_2_34-0">[32]
- WASP-43 b[33]
- CoRoT-2 bet_al.''_2018Figure_2_36-0">[34]
- WASP-18 b[35]
- TRAPPIST-1 e[36]
- Kepler-7 b
- LHS 3844 b[37]
- Wolf 1069 b[38]
- GJ 1214 b[39] - [40]
Notes et références
Notes
- L'aplatissement est défini comme l'écart relatif entre le rayon équatorial moyen et le rayon polaire moyen : .
- Demi-axe long = rayon équatorial long ; demi-axe intermédiaire = rayon équatorial court ; demi-axe court = rayon polaire.
Références
- IAU - WGCCRE, sur le site de l'USGS Astrogeology Science Center.
- et_al.''_1980-2" class="mw-reference-text">Davies et al. 1980.
- Archinal et al. 2011a.
- Archinal et al. 2011b.
- Archinal et al. 2013.
- Archinal et al. 2018.
- Archinal et al. 2019.
- "Solar coordinates" dans le Glossary of Solar-Terrestrial Terms.
- et_al.''_2018-10" class="mw-reference-text">Archinal et al. 2018.
- La capture de Mercure en résonance spin-orbite 3:2 s’explique par le mouvement chaotique de son orbite, Observatoire de Paris, .
- De Mercure à Pluton, planètes et satellites, Pierre Humbert, 1937, p. 10-19
- Gordon Pettengill et Rolf Dyce, « A Radar Determination of the Rotation of the Planet Mercury », Nature, no 206, , p. 1240 (lire en ligne)
- « USGS Astrogeology: Rotation and pole position for the Sun and planets (IAU WGCCRE) » (consulté le )
- Surface coordinates and cartography of Mercury, M. E. Davies et R. M. Batson, J. Geophys. Res., 80(17), 2417–2430 (1975). DOI 10.1029/JB080i017p02417
- Davies, M.E. et al., Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites, vol. 63, (DOI 10.1007/BF00693410, Bibcode 1996CeMDA..63..127D), p. 127
- « USGS Astrogeology: Rotation and pole position for the Sun and planets (IAU WGCCRE) » (consulté le )
- « The Magellan Venus Explorer's Guide » (consulté le )
- (en) ESA Mars Express News – 19 août 2004 « Where is zero degrees longitude on Mars? »
- Atlas of Uranian Satellites 1:2,000,000 Topographic Series Miranda, 1988.
- Atlas of Uranian Satellites 1:5,000,000 Topographic Series Ariel, 1988.
- Atlas of Uranian Satellites 1:10,000,000 Topographic Series Umbriel, Titania, and Oberon, 1988.
- Davies, Rogers et Colvin 1991.
- Raymond et Roatsch 2015.
- et_al.''_2016-26" class="mw-reference-text">Park et al. 2016.
- « Buie : Pluto Research », sur swri.edu (consulté le ).
- Mottola et al. 2020.
- [Lauretta et al. 2019] (en) D. S. Lauretta et al., « The unexpected surface of asteroid (101955) Bennu » [« La surface inattendue de l'astéroïde (101955) Bénou »], Nature, (lire en ligne)Voir la figure 1.c) : « A 30-m boulder that defines the prime meridian... », c'est-à-dire « Un rocher mesurant 30 mètres qui définit le premier méridien… ».
- (en) Union astronomique internationale, « First Official Names Given to Features on Asteroid Bennu » [« Premiers noms officiels donnés à des formations sur l'astéroïde Bénou »], Press Releases, no iau2002, (lire en ligne)
- « Jan. 21, 2019. What's new », sur JAXA Hayabusa2 project (consulté le ).
- (en) Finding my way around comet Churyumov-Gerasimenko, Emily Lakdawalla, .
- « More Informative Mapping of Exoplanetary Peekaboos », sur aasnova.org (consulté le ).
- et_al.''_2016Figure_2-34" class="mw-reference-text">Demory et al. 2016, Figure 2.
- (en) George Dvorsky, « This Extreme Exoplanet Just Got Its Own Weather Map », sur gizmodo.com, io9, (consulté le ).
- et_al.''_2018Figure_2-36" class="mw-reference-text">Dang et al. 2018, Figure 2.
- https://arxiv.org/pdf/1901.08640.pdf : Figure 1.
- (en) « Detectability of Molecular Signatures on TRAPPIST-1e through Transmission Spectroscopy Simulated for Future Space-Based Observatories - Astrobiology », sur astrobiology.com (consulté le ).
- Tobias G. Meier, Dan J. Bower, Tim Lichtenberg, Paul J. Tackley et Brice-Olivier Demory, « Hemispheric Tectonics on LHS 3844b », The Astrophysical Journal Letters, vol. 908, no 2, , p. L48 (arXiv 2103.02374).
- D. Kossakowski, « The CARMENES search for exoplanets around M dwarfs, Wolf 1069 b: Earth-mass planet in the habitable zone of a nearby, very low-mass star », Astronomy & Astrophysics, (arXiv 2301.02477, lire en ligne).
- https://arxiv.org/abs/2305.06240
- https://www.mpia.de/news/science/2023-06-gj1214b
Bibliographie
Rapports du groupe de travail de l'UAI sur les coordonnées cartographiques et les éléments de rotation et documents analogues
- [Davies et al. 1980] M. E. Davies et al., « Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements of the Planets and Satellites », Celestial mechanics, vol. 22, , p. 205-230 (lire en ligne)
- [Seidelmann et al. 2007] P. K. Seidelmann et al., « Report of the IAU/IAG Working Group on Cartographic Coordinates and Rotational Elements: 2006 » [« Rapport du groupe de travail de l'UAI/AIG sur les coordonnées cartographique et les éléments de rotation : 2006 »], Celestial Mechanics and Dynamical Astronomy, no 98, , p. 155-180 (DOI 10.1007/s10569-007-9072-y, Bibcode 2007CeMDA..98..155S, lire en ligne)
- [Archinal et al. 2011a] B. A. Archinal et al., « Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009 » [« Rapport du groupe de travail de l'UAI sur les coordonnées cartographique et les éléments de rotation : 2009 »], Celestial Mechanics and Dynamical Astronomy, no 109, , p. 101-135 (DOI 10.1007/s10569-010-9320-4, Bibcode 2011CeMDA.109..101A, lire en ligne)
- [Archinal et al. 2011b] B. A. Archinal et al., « Erratum to: Reports of the IAU Working Group on Cartographic Coordinates and Rotational Elements:2006 & 2009 » [« Erratum à : Rapports du groupe de travail de l'UAI sur les coordonnées cartographique et les éléments de rotation : 2006 & 2009 »], Celestial Mechanics and Dynamical Astronomy, no 110, , p. 401-403 (DOI 10.1007/s10569-011-9362-2, Bibcode 2011CeMDA.110..401A, lire en ligne)
- [Archinal et al. 2013] B. A. Archinal et al., « Recommended Coordinate System for (4) Vesta » [« Système de coordonnées recommandé pour (4) Vesta »], site de l'USGS Astrogeology Science Center, (lire en ligne)
- [Archinal et al. 2018] B. A. Archinal et al., « Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015 » [« Rapport du groupe de travail de l'UAI sur les coordonnées cartographique et les éléments de rotation : 2015 »], Celestial Mechanics and Dynamical Astronomy, no 130, (en ligne le ), p. 22 (DOI 10.1007/s10569-017-9805-5, lire en ligne)
- [Archinal et al. 2019] B. A. Archinal et al., « Correction to: Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015 » [« Correction à : Rapport du groupe de travail de l'UAI sur les coordonnées cartographique et les éléments de rotation : 2015 »], Celestial Mechanics and Dynamical Astronomy, no 131, (en ligne le ), p. 61 (DOI 10.1007/s10569-019-9925-1, lire en ligne)
Autres articles
- [Dang et al. 2018] « Detection of a westward hotspot offset in the atmosphere of hot gas giant CoRoT-2b » [« Détection d'un décalage du point chaud vers l'ouest dans l'atmosphère de la géante gazeuse chaude CoRoT-2 b »], Nature Astronomy, (DOI 10.1038/s41550-017-0351-6, arXiv 1801.06548.pdf, lire en ligne)Les co-auteurs de l'article sont, outre Lisa Dang, Nicolas B. Cowan, Joel C. Schwartz, Emily Raucher, Michael Zhang, Heather A. Knutson, Michael Line, Ian Dobbs-Dixon, Drake Deming, Sudarsan Sundararajan, Jonathan J. Fortney et Ming Zhao.
L'article a été reçu le 15 août 2017, accepté le 28 novembre de la même année puis publié en ligne le 22 janvier 2018. - [Demory et al. 2016] Brice-Olivier Demory et al., « A map of the large day–night temperature gradient of a super-Earth exoplanet » [« Une carte du grand gradient de température d'une exoplanète de type super-Terre »], Nature, vol. 532, , p. 207 (DOI 10.1038/nature17169, lire en ligne)
- « Chapter 2. Cartographic Standards », Planetary Data System, National Aeronautics and Space Administration, date indéterminée (lire en ligne)
- [Park et al. 2016] (en) R. S. Park et al., « A partially differentiated interior for (1) Ceres deduced from its gravity field and shape » [« Un intérieur partiellement différencié pour (1) Cérès déduit de son champ de gravité et de sa forme »], Nature, vol. 537, no 7621, , p. 515-517 (DOI 10.1038/nature18955, Bibcode 2016Natur.537..515P)Les co-auteurs de l'article sont, outre R. S. Park, A. S. Konopliv, B. G. Bills, N. Rambaux, J. C. Castillo-Rogez, C. A. Raymond, A. T. Vaughan, A. I. Ermakov, M. T. Zuber, R. R. Fu, M. J. Toplis, C. T. Russell, A. Nathues, F. Preusker.
- [Raymond et Roatsch 2015] C. Raymond et T. Roatsch, « Ceres Coordinate System Description » [« Description du système de coordonnées de Cérès »], PDS Asteroid/Dust Archive, (lire en ligne).

