Topologie (circuits électriques)
La topologie d'un circuit électronique est la forme prise par le réseau d'interconnexions des composantes du circuit. Des valeurs différentes des composantes sont considérées comme formant la même topologie. La topologie ne se préoccupe pas de la disposition physique des composantes d'un circuit, ni de leur position sur un schéma électrique (diagramme de circuit). Similairement au concept mathématique de topologie, elle ne se préoccupe que des connexions qui existent entre les composantes. Il peut y avoir de nombreux schémas de circuits et dispositions physiques correspondant tous à la même topologie.
À strictement parler, remplacer une composante par une autre d'un type totalement différent constitue toujours la même topologie. Cependant, dans certains contextes, elles peuvent être grossièrement décrites comme des topologies différentes. Par exemple, interchanger les inductances et les condensateurs dans un filtre passe-bas donne un filtre passe-haut. Ces topologies peuvent être décrites comme des topologies passe-haut et passe-bas même si la topologie du réseau est identique. Un terme plus juste pour ces classes d'objets (c'est-à-dire un réseau où on spécifie le type de composante, mais pas la valeur absolue) est réseau prototype .
La topologie des réseaux électroniques est liée à la topologie mathématique. En particulier, pour les réseaux contenant seulement des dispositifs à deux terminaux, on peut considérer la topologie de circuit comme une application de la théorie des graphes. Dans une analyse de réseau d'un point de vue topologique d'un tel circuit, les nœuds du réseau sont les sommets et les mailles les arêtes de la théorie des graphes.
On peut étendre la théorie des graphes standard pour traiter les composantes actives et les dispositifs multi-terminaux tels que les circuits intégrés. On peut aussi utiliser les graphes dans l'analyse de réseaux infinis.
Schémas électriques (diagrammes de circuits)
Les schémas électriques de cet article suivent les conventions habituelles en électronique[1]. Les lignes représentent les conducteurs, les petits cercles pleins les jonctions des conducteurs et les petits cercles ouverts les bornes de connexion à l'extérieur. Dans la plupart des cas, les rectangles représentent les impédances. Un schéma de circuit réalisable utiliserait des symboles spécifiques pour les résistances, inductances, condensateurs et autres composantes, mais la topologie ne se préoccupe pas du type de composante dans le réseau. Le symbole pour une impédance générale est donc utilisé à la place.
Nomenclature des topologies
Souvent les topologies possèdent un nom référant à leur apparence sur un diagramme. La plupart des circuits peuvent être dessinés de diverses manières et, par conséquent, avoir une variété de noms. Par exemple, les trois circuits illustrés à la figure 1.1 semblent tous différents, mais leurs topologies sont identiques[2].
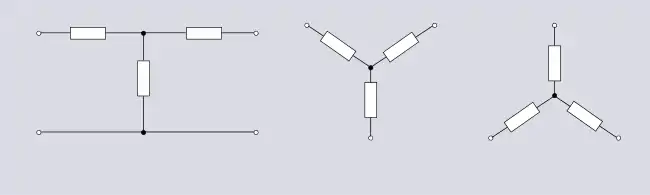
Cet exemple montre la convention courante consistant à nommer les topologies selon une lettre de l'alphabet similaire. L'alphabet grec peut également être utilisé, comme dans la topologie Π (pi) et la topologie Δ (delta).
Topologies en série et parallèles
Pour un réseau à deux mailles, seulement deux topologies sont possibles: en série et parallèle.
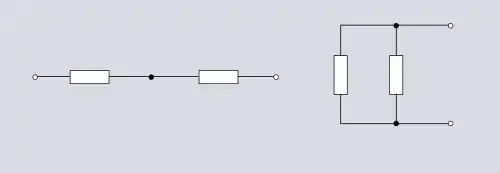
Même pour cette topologie simple, il existe des variations dans la façon de représenter le circuit.
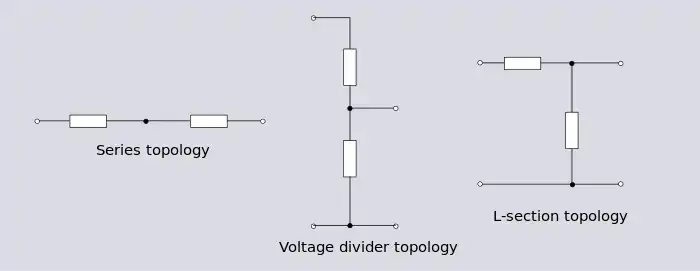
Pour un réseau à trois mailles, quatre topologies possibles existent.
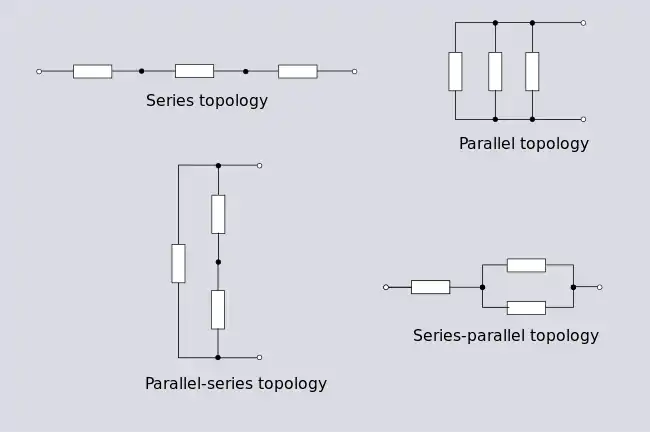
À noter que la topologie en série-parallèle ('parallel-series' sur le diagramme) est une autre représentation de la topologie Delta discutée plus loin.
On peut construire des topologies en série et parallèles en y ajoutant toujours plus de mailles jusqu'à l'infini. Le nombre de topologies uniques pouvant être obtenues avec n mailles est de 2n-1. Le nombre total de topologies uniques pouvant être obtenues avec au plus n mailles est de 2n-1[3].
Topologies Y et Δ
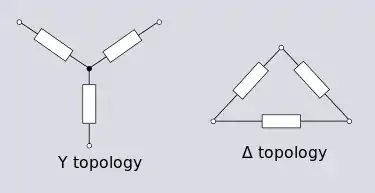
Les topologies Y et Δ sont importantes en analyse de réseau linéaire, car elles constituent les réseaux à trois terminaux les plus simples possibles. Une transformée Y-Δ existe pour les circuits linéaires. Il s'agit d'une transformation importante, car certains réseaux ne peuvent être analysés en termes de combinaisons en série et parallèles. On rencontre souvent ces réseaux dans les circuits de puissance triphasés puisque ce sont les deux topologies les plus courantes pour les enroulements de moteur ou de transformateur triphasés.
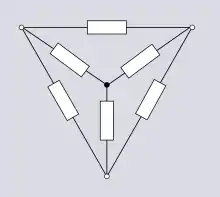
Un exemple d'un tel réseau est illustré à la figure 1.6, où on a un réseau Y connecté en parallèle avec un réseau Δ. Supposons que l'on veuille calculer l'impédance entre deux nœuds du réseau. Souvent, cela peut se faire par applications successives des règles de combinaison des impédances série ou parallèle. C'est toutefois impossible dans ce réseau, car il faut utiliser la transformée Y-Δ en plus des règles en série et parallèle[4]. La topologie Y se nomme également topologie en étoile. Cependant, la topologie en étoile peut aussi référer au cas plus général de n mailles connectées au même nœud plutôt que trois[5].
Topologies de filtre simples
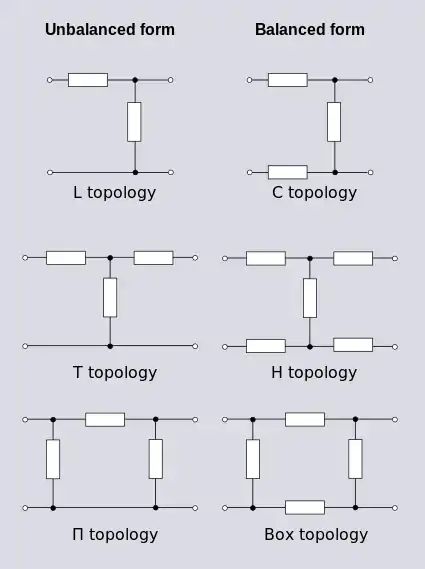
Les topologies dans la figure 1.7 sont communément utilisées dans la conception de filtres et d'atténuateurs. La topologie en L est identique à celle du diviseur de potentiel. La topologie en T est identique à celle en Y. La topologie en Π est identique à celle en Δ.
On peut voir toutes ces topologies comme des sections de topologie en échelle. Les sections plus longues seraient décrites comme une topologie en échelle. On analyse et on caractérise souvent ces types de circuits en termes de réseau à deux ports[6].
Topologie de pont
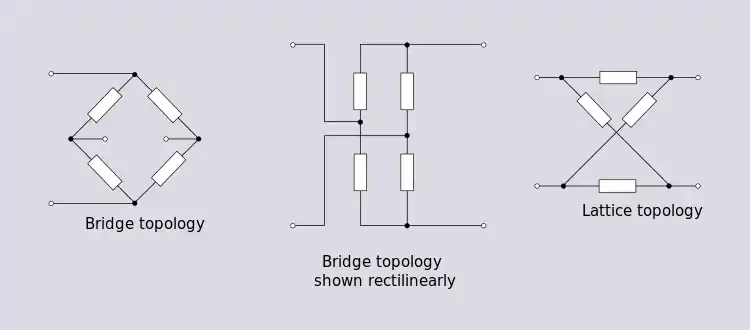
La topologie de pont est une topologie importante avec de nombreuses utilisations dans des applications linéaires et non linéaires. Parmi ces nombreuses applications se trouvent le redresseur de pont, le pont de Wheatstone et l'égaliseur de phase de réseau. La topologie de pont peut être représentée de plusieurs façons dans les schémas de circuits. La première représentation de la figure 1.8 est la représentation traditionnelle d'un circuit en pont. La deuxième montre clairement l'équivalence entre la topologie de pont et une topologie dérivée par des combinaisons en série et parallèles. La troisième est plus communément appelée topologie en treillis. Bien que l'équivalence topologique n'y soit pas évidente, on peut la voir en visualisant qu'on déplace le nœud supérieur gauche à droite du nœud supérieur droit.
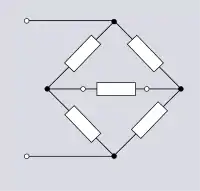
Il est normal de qualifier un réseau de topologie de pont uniquement si on l'utilise comme un réseau à deux ports où les ports d'entrée et de sortie sont chacun constitués d'une paire de nœuds diagonalement opposés. On peut considérer la topologie de boîte de la figure 1.7 identique à la topologie de pont, mais dans le cas du filtre, les ports d'entrée et de sortie seront chacun une paire de nœuds adjacents. On inclut parfois dans la topologie de pont la composante de chargement (ou d'indication nulle) sur le port de sortie du pont, tel qu'illustré à la figure 1.9[7].
Topologies pontée en T et à double T
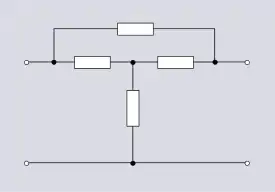
La topologie pontée en T est dérivée de la topologie de pont. De nombreuses topologies dérivées existent.
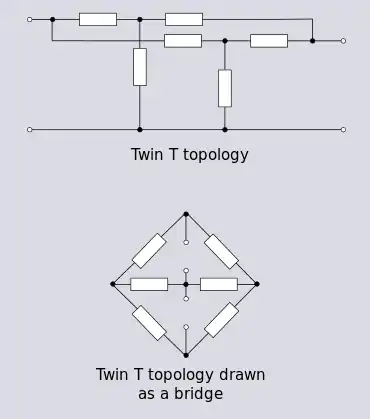
Une topologie à double T existe aussi avec des applications pratiques où il est souhaitable que les entrées et les sorties partagent une borne de masse. Un exemple d'un tel cas est lorsque les connexions d'entrée et de sortie sont faites avec une topologie coaxiale. Une topologie de pont normale ne permet pas la connexion entre une borne d'entrée et de sortie. Pour cette raison, la topologie à double T est utilisée dans les cas où un pont serait par ailleurs utilisé pour des applications d'équilibrage ou de mesure nulle. Cette topologie est également utilisée dans l' oscillateur à double T comme générateur d'onde sinusoïdale. La partie inférieure de la figure 1.11 montre une topologie à double T redessinée dans le but de souligner la connexion avec la topologie de pont[8].
Topologies infinies
On peut étendre la topologie en échelle à l'infini. Elle est très utilisée dans la conceptions de filtres. La topologie en échelle présente de nombreuses variantes. Voir les pages sur la topologie de filtre électronique et le filtre d'image composite.
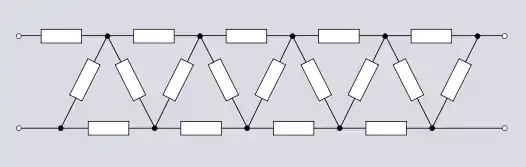
La forme équilibrée de la topologie en échelle peut être considérée comme le graphe de l'arête d'un prisme d'ordre arbitraire. L'arête d'un anti-prisme forme une topologie en anti-échelle. La topologie en anti-échelle présente une application dans les circuits multiplicateurs de tension, dont le générateur Cockcroft-Walton. Il existe également une version pleine onde du générateur Cockcroft-Walton utilisant une topologie double en anti-échelle[9].
On peut aussi former des topologies infinies en cascadant plusieurs sections de topologies simples, comme des sections en treillis ou pontées en T. On rencontre de telles chaînes infinies de sections de réseau dans l'analyse théorique et la simulation artificielle des lignes de transmission, mais elles sont rarement utilisées comme mise en œuvre réalisable d'un circuit[10].
Composants avec plus de deux terminaux
Les circuits contenant des composantes avec trois terminaux ou plus augmentent considérablement le nombre possible de topologies. Inversement, le nombre de circuits différents représentés par une topologie diminue. Dans de nombreux cas, le circuit est facilement reconnaissable à partir de la topologie, même avec des composantes spécifiques non identifiées.
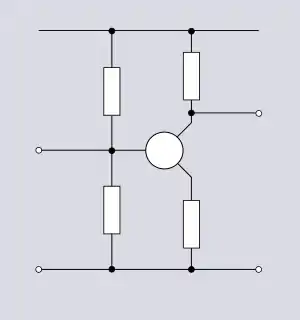 Figure 1.14 . Topologie d'amplificateur de base, tel l'amplificateur à transistor à jonction bipolaire à émetteur commun |
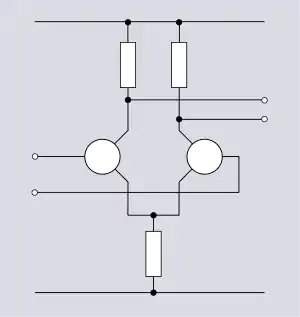 Figure 1.15 . Amplificateur équilibré, tel l'amplificateur de paire à longue queue |
Avec des circuits plus complexes, la description peut spécifier une fonction de transfert entre les ports du réseau au lieu de la topologie des composantes[11].
Théorie des graphes
La théorie des graphes est la branche des mathématiques traitant des graphes. En analyse de réseau, on utilise largement les graphes pour représenter le réseau analysé. Le graphe d'un réseau ne capture que les aspects du réseau liés à sa connectivité (ou topologie). Il est utile de représenter et généraliser un réseau, car de nombreuses équations de réseau sont invariantes sur des réseaux de même topologie, dont les équations dérivées des lois de Kirchhoff et du théorème de Tellegen[12].
Histoire
On utilisa la théorie des graphes dans l'analyse de réseau de réseaux passifs linéaires presque dès le moment de la formulation des lois de Kirchhoff. Gustav Kirchhoff lui-même utilisa les graphes comme représentation abstraite d'un réseau dans son analyse des boucles de circuits résistifs en 1847[13]. On généralisa ensuite cette approche aux circuits RLC, remplaçant les résistances par des impédances. En 1873, James Clerk Maxwell fournit le complémentaire de cette analyse avec l'analyse des nœuds[14] - [15]. Maxwell fut également responsable du théorème topologique selon lequel le déterminant de la matrice d'admission nodale est égal à la somme de tous les produits des entrées dans l'arbre. En 1900, Henri Poincaré introduisit l'idée de représenter un graphe par sa matrice d'incidence [16], fondant ainsi le domaine de la topologie algébrique. En 1916, Oswald Veblen appliqua la topologie algébrique de Poincaré à l'analyse de Kirchhoff[17]. Veblen fut également responsable de l'introduction de l'arbre couvrant pour faciliter le choix d'un ensemble compatible de variables de réseau[18].
Le catalogage complet des graphes de réseau appliqués aux circuits électriques commença avec Percy MacMahon en 1891. Il limita son enquête aux combinaisons en série et parallèles. MacMahon nomma ces graphes chaînes de joug[note 1]. En 1932, Ronald M. Foster classa les graphes par leur nullité ou leur rang et fournit des diagrammes montrant tous ceux avec un petit nombre de nœuds. Ce travail naquit d'une enquête préalable lors de sa collaboration avec George Campbell en 1920 sur des répéteurs téléphoniques à quatre ports. Il produisit 83 539 graphes distincts[19].
Pendant longtemps, la topologie de la théorie des circuits électriques ne s'est préoccupée que les réseaux passifs linéaires. Les développements récents dans le domaine des dispositifs et circuits semi-conducteurs ont cependant nécessité de nouveaux outils topologiques. Une énorme augmentation de la complexité des circuits a conduit à l'utilisation de l'analyse combinatoire dans la théorie des graphes dans le but d'améliorer l'efficacité du calcul informatique[18].
Graphes et schémas électriques
On classe généralement les réseaux selon le type d'éléments électriques les composant. Dans un schéma électrique, ces types d'éléments possèdent chacun leur symbole unique. Les réseaux résistifs sont des réseaux à un seul élément, composés uniquement d'éléments R. De même, les réseaux capacitifs ou inductifs sont de type à un élément, respectivement C ou L. Les circuits RC, RL et LC sont des réseaux simples à deux éléments. Le circuit RLC, quant à lui, est le plus simple réseau à trois éléments. Le réseau en échelle LC couramment utilisé dans les filtres passe-bas peut avoir de nombreux éléments, mais demeure quand même un autre exemple de réseau de type à deux éléments[20].
Inversement, la topologie ne s'intéresse qu'à la relation géométrique entre les éléments d'un réseau, et non au type d'éléments. Le cœur d'une représentation topologique d'un réseau est le graphe du réseau. Les éléments sont représentés comme les arêtes du graphe. Une arête est dessinée comme une ligne terminée par des points ou de petits cercles desquels d'autres arêtes (éléments) peuvent émaner. En analyse de circuits, les arêtes du graphe se nomment des mailles. Les points sont appelés les sommets du graphe et représentent les nœuds du réseau. Les termes nœud et sommet peuvent être utilisés de manière interchangeable lors de la discussion de graphes de réseaux. La figure 2.2 montre une représentation graphique du circuit de la figure 2.1[21].
De plus, les graphes utilisés dans l'analyse de réseau sont généralement à la fois des graphes orientés, pour capturer la direction du flux et de la tension du courant, et des graphes étiquetés, pour capturer l'unicité des mailles et des nœuds. Par exemple, un graphe composé d'un carré de mailles serait toujours le même graphe topologique si on échangeait deux mailles, à moins que les mailles ne soient étiquetées de manière unique. Dans les graphes dirigés, les deux nœuds auxquels une maille se connecte sont désignés comme les nœuds source et cible. En règle générale, ceux-ci seront indiqués par une flèche dessinée sur la maille[22].
Incidence
L'incidence est l'une des propriétés de base d'un graphe. Une arête connectée à un sommet est dite incidente sur ce sommet. L'incidence d'un graphe peut être capturée dans une matrice appelée matrice d'incidence. En fait, la matrice d'incidence est une représentation mathématique alternative du graphe où le dessin devient superflu. Les lignes de la matrice correspondent aux nœuds et les colonnes, aux mailles. Les éléments de la matrice sont soit zéro, pour aucune incidence, soit un, pour une incidence entre le nœud et la maille. La direction dans les graphes dirigés est indiquée par le signe de l'élément[18] - [23].
Équivalence
Les graphes sont équivalents si l'on peut transformer l'un en l'autre par déformation. La déformation peut inclure les opérations de translation, de rotation et de réflexion, le pli et l'étirement des mailles, et le croisement ou le nouage des mailles. On qualifie de congruents deux graphes équivalents par déformation[24].
Dans le domaine des réseaux électriques, il existe deux transformations supplémentaires qu'on considère comme aboutissant à des graphes équivalents sans qu'elles ne produisent de graphes congruents. La première est l'échange de mailles connectées en série. Il s'agit du double échange de mailles connectées en parallèle qu'on peut obtenir par déformation sans qu'une règle spéciale ne soit nécessaire. La seconde concerne les graphes divisés en deux ou plusieurs parties distinctes, c'est-à-dire un graphe avec deux ensembles de nœuds où chaque ensemble possède un nœud dépourvu de maille incidente. Deux de ces parties distinctes sont considérées comme un graphe équivalent à un seul où les parties sont jointes en combinant un nœud de chacun en un seul nœud. De même, un graphe qu'on peut diviser en deux parties distinctes en divisant un nœud en deux est également considéré comme équivalent[25].
Arbres et liens
Un arbre est un graphe dans lequel tous les nœuds sont connectés par des mailles, soit directement ou indirectement, sans former de boucles fermées. Puisqu'il n'y a pas de boucles fermées, il n'y a pas de courant dans un arbre. Dans l'analyse de réseau, nous nous intéressons aux arbres couvrants, c'est-à-dire aux arbres connectant chaque nœud dans le graphe du réseau. Ici, sauf indication contraire, un arbre couvrant est défini par un arbre non qualifié. Un graphe de réseau donné peut contenir plusieurs arbres différents. Les mailles retirées d'un graphe pour former un arbre se nomment liens, tandis que les mailles restant dans l'arbre se nomment brindilles. Pour un graphe à n nœuds, le nombre de mailles dans chaque arbre, t, doit être;
Une relation importante pour l'analyse des circuits est:
où b est le nombre de mailles du graphe et ℓ, le nombre de liens retirés pour former l'arbre[26].
Ensembles des liens et ensembles des coupes
Le but de l'analyse de circuit est de déterminer tous les courants et tensions de maille du réseau. Ces variables de réseau ne sont pas toutes indépendantes. Les tensions de maille sont liées aux courants de maille par la fonction de transfert des éléments les composant. Une solution complète du réseau ne peut donc qu'être soit uniquement en termes de courants de maille, soit uniquement en termes de tensions de maille. De plus, tous les courants de maille ne sont pas indépendants. Le nombre minimum de courants de maille requis pour une solution complète est l. Cela est une conséquence du fait qu'un arbre a l liens supprimés et qu'il ne peut y avoir de courants dans un arbre. Comme le courant est nul dans les mailles restantes de l'arbre, elles ne peuvent être indépendantes des courants de liaison. Les courants de maille choisis comme ensemble de variables indépendantes doivent constituer un ensemble associé aux liens d'un arbre: on ne peut pas choisir arbitrairement l mailles[27].
En termes de tensions de maille, on peut obtenir une solution complète du réseau avec t tensions de maille. Cela est une conséquence du fait que le court-circuitage de toutes les mailles d'un arbre entraîne une tension nulle partout. Par conséquent, les tensions de liaison ne peuvent pas être indépendantes des tensions de maille de l'arbre[28].
Une approche analytique courante consiste à résoudre pour les courants de boucle plutôt que pour les courants de maille. Les courants de maille se calculent alors en termes de courants de boucle. Encore une fois, on ne peut choisir arbitrairement l'ensemble des courants de boucle. Dans le but de garantir un ensemble de variables indépendantes, les courants de boucle doivent être associés à un ensemble de boucles spécifique. Cet ensemble de boucles est constitué des boucles formées en remplaçant une seule liaison d'un arbre donné du graphe du circuit à analyser. Puisque le remplacement d'une seule liaison dans un arbre forme une boucle unique spécifique, le nombre de courants de boucle ainsi définis est égal à l. À noter que le terme boucle dans ce contexte n'a pas le même sens que dans la théorie des graphes. On nomme ensemble des liens l'ensemble des mailles formant une boucle donnée[note 2]. On forme l'ensemble des équations du réseau en égalisant les courants de boucle à la somme algébrique des courants de maille de l'ensemble des liens[29].
On peut choisir un ensemble de courants de boucle indépendants sans se référer aux arbres et aux ensembles de liens. Une condition suffisante et non nécessaire pour choisir un ensemble de boucles indépendantes est que chaque boucle choisie comprenne au moins une maille pas précédemment incluse dans les boucles déjà choisies. Un choix particulièrement simple est celui utilisé dans l'analyse des mailles, où toutes les boucles sont choisies pour être des mailles[note 3]. On ne peut appliquer l'analyse de maille que si l'on peut schématiser le graphe sur un plan ou une sphère sans aucun croisement de mailles. De tels graphes se nomment graphes planaires. Pouvoir schématiser sur un plan et pouvoir schématiser sur une sphère constituent des conditions équivalentes. Tout graphe fini schématisé sur un plan peut être réduit jusqu'à ce qu'il puisse se schématiser sur une petite région d'une sphère. Inversement, on peut étirer un maillage de n'importe quel graphe schématisé sur une sphère jusqu'à ce que l'espace à l'intérieur occupe presque toute la sphère. Le graphe entier n'occupe alors plus qu'une petite région de la sphère. Il s'agit du même cas que le premier, donc on pourra également schématiser le graphe sur un plan[30].
Il existe une approche pour choisir les variables du réseau qui utilise les tensions. Elle est analogue et duale à la méthode du courant de boucle. Ici, la variables primaire est la tension associée à une paire de nœuds et les tensions de maille sont trouvées en fonction de celle-ci. Toujours dans cette méthode, un arbre particulier du graphe doit être choisi afin de garantir que toutes les variables soient indépendantes. Le dual de l'ensemble des liens est l'ensemble des coupes. On forme un ensemble des liens en permettant à tous les liens de graphe sauf un d'être en circuit ouvert. On forme un ensemble des coupes en permettant à toutes les mailles de l'arbre sauf une d'être court-circuitées. L'ensemble des coupes se compose de la maille de l'arbre qui n'a pas été court-circuitée et des liaisons qui ne sont pas court-circuitées par les autres mailles de l'arbre. Un ensemble de coupes dans un graphe produit deux sous-graphes disjoints, c'est-à-dire qu'il coupe le graphe en deux parties. Il constitue d'ailleurs l'ensemble minimal de mailles nécessaires pour ce faire. On forme l'ensemble des équations de réseau en égalant les tensions de la paire de nœuds à la somme algébrique des tensions de maille de l'ensemble des coupes[31]. Le dual de l'analyse de maillage est l'analyse nodale[32].
Nullité et rang
La nullité N d'un graphe ayant s parties distinctes et b mailles est définie par:
La nullité d'un graphe correspond au nombre de degrés de liberté dans son ensemble d'équations du réseau. Pour un graphe planaire, la nullité est égale au nombre de mailles du graphe[33].
Le rang R d'un graphe est défini par:
Le rang joue le même rôle en analyse nodale que la nullité en analyse du maillage: il donne le nombre d'équations de tension des nœuds requises. Le rang et la nullité sont des concepts duals et sont liés par [34]
Résolution des variables de réseau
Une fois choisi un ensemble de variables géométriquement indépendantes, on exprime l'état du réseau en fonction de celles-ci. Le résultat est un ensemble d'équations linéaires indépendantes qu'il faut résoudre simultanément afin de trouver les valeurs des variables du réseau. Cet ensemble d'équations peut être exprimé en format matriciel, menant à une matrice de paramètres caractéristique du réseau. Les matrices de paramètres prennent la forme d'une matrice d'impédance si les équations viennent de l'analyse de boucle, et la forme d'une matrice d'admission si les équations viennent de l'analyse de nœud[35].
Ces équations peuvent être résolues de plusieurs manières connues. Une méthode consiste à éliminer systématiquement les variables[36]. Une autre méthode, la règle de Cramer, utilise les déterminants pour obtenir une expression directe de la variable inconnue en termes de ceux-ci. On obtient ainsi une expression compacte pour la solution. Cependant, pour des réseaux moins triviaux, l'effort de calcul augmente considérablement lorsqu'on travaille manuellement[37].
Dualité
Deux graphes sont duals lorsque la relation entre les mailles et les paires de nœuds dans l'un est la même que la relation entre les mailles et les boucles dans l'autre. On peut trouver le dual d'un graphe entièrement par une méthode graphique[38].
Le dual d'un graphe est un autre graphe. Dans un graphe, pour un arbre donné, l'ensemble complémentaire de mailles (c'est-à-dire les mailles qui ne se trouvent pas dans l'arbre) forme un arbre dans le graphe dual. L'ensemble des équations de boucle de courant associées aux ensembles des liens du graphe et de l'arbre originaux sont identiques à l'ensemble des équations de paire de nœuds de tension associées aux ensembles des coupes du graphe dual[39].
Le tableau suivant répertorie les concepts topologiques duals liés à la théorie des circuits[40].
| Courant | Tension |
| Arbre | Labyrinthe |
| Maille | Maille |
| Maillage | Nœud |
| Boucle | Paire de nœuds |
| Lien | Branche d'arbre |
| Ensemble des liens | Ensemble des coupes |
| Court-circuit | Circuit ouvert |
| Connexion parallèle | Connexion en série |
| Nullité | Rang |
Le dual d'un arbre se nomme un labyrinthe [note 4] Il se compose d'espaces reliés par des liens tout comme l'arbre se compose de nœuds reliés par des branches d'arbre[41].
Tout graphe ne possède pas de dual. La dualité nécessite que chaque ensemble de liens ait un ensemble de coupes dual dans le graphe dual. Cette condition est remplie si et seulement si le graphe peut être schématisé sur une sphère sans croisement de mailles. Pour bien le voir, notons qu'un ensemble de liens est nécessaire pour "lier" un graphe en deux parties et que son dual, l'ensemble de coupes, est nécessaire pour couper un graphe en deux parties. Le graphe d'un réseau fini qu'on ne peut pas schématiser sur une sphère nécessitera un tore de dimension n. Un ensemble de liens passant à travers un trou dans un tore ne réussira pas à lier le graphe en deux parties. Par conséquent, le graphe dual ne sera pas coupé en deux et ne contiendra pas l'ensemble des coupes requis. Il en résulte que seuls les graphes planaires ont des duals[42].
On ne peut pas non plus former de duals pour les réseaux contenant des inductances mutuelles, car aucun élément capacitif correspondant n'existe. On peut développer des circuits équivalents possédant des duals, mais on ne peut pas directement former le dual d'une inductance mutuelle[43].
Élimination des nœuds et des mailles
Les opérations sur un ensemble d'équations de réseau ont un sens topologique puvant aider à visualiser la situation. L'élimination d'une tension de nœud d'un ensemble d'équations de réseau correspond topologiquement à l'élimination de ce nœud du graphe. Pour un nœud connecté à trois autres nœuds, cela correspond à la transformée Y-Δ. La transformation peut s'étendre à un plus grand nombre de nœuds connectés. Elle est alors connue sous le nom de transformation en étoile[44].
L'inverse de cette transformée est la transformée Δ-Y. Elle correspond analytiquement à l'élimination d'un courant de maille et topologiquement à l'élimination d'une maille. Cependant, éliminer un courant de maillage dont le maillage a des mailles communes avec un nombre arbitraire d'autres mailles donnera généralement un graphe irréalisable. En effet, le graphe de la transformation de l'étoile générale est un graphe qu'on ne peut pas schématiser sur une sphère, car il contient des polygones d'étoiles et donc plusieurs croisements. Le dual d'un tel graphe ne peut pas exister, mais il est néanmoins nécessaire pour représenter une élimination généralisée du maillage[44].
Couplage mutuel
Dans la représentation graphique classique des circuits, il n'existe aucun moyen de représenter explicitement les couplages inductifs mutuels, comme cela se produit dans un transformateur. De tels composantes peuvent entraîner un graphe déconnecté avec plus d'une partie distincte. Pour faciliter l'analyse, un graphe à plusieurs parties peut être combiné en un seul graphe. Pour ce faire, on unifie un nœud de chaque partie en un seul nœud.Le comportement théorique du circuit ne s'en trouve pas modifié, de sorte que l'analyse effectuée sur celui-ci est toujours valide. Cependant, en pratique, si un tel circuit devait être mis en œuvre, le comportement changerait, car le circuit détruirait l'isolement entre les pièces. Un exemple serait un transformateur mis à la terre des côtés primaire et secondaire. Le transformateur fonctionnerait toujours comme un transformateur avec le même rapport de tension, mais ne pourrait plus être utilisé comme transformateur d'isolement[45].
Des techniques de théorie des graphes plus récentes peuvent gérer les composantes actives, elles aussi problématiques dans la théorie conventionnelle. Ces nouvelles techniques peuvent également gérer les couplages mutuels[46].
Composantes actives
Deux approches de base existent pour gérer les couplages mutuels et les composantes actives. Dans le premier, Samuel Jefferson Mason a introduit en 1953 les graphes de flux de signaux[47]. Les graphes de flux de signaux sont des graphes orientés pondérés. Il les a utilisés pour analyser des circuits contenant des couplages mutuels et des réseaux actifs. Le poids d'une arête dirigée dans ces graphes représente un gain, tel que dans un amplificateur. En général, les graphes de flux de signaux ne correspondent pas à la topologie de l'agencement physique des composantes, contrairement aux graphes dirigés réguliers décrits ci-dessus[46].
La deuxième approche consiste à étendre la méthode classique afin d'y inclure des couplages mutuels et des composantes actives. Plusieurs méthodes ont été proposées pour y parvenir. Dans l'une, deux graphes sont construits, l'un représentant les courants dans le circuit et l'autre les tensions. Les composantes passives auront des mailles identiques dans les deux arborescences, mais pas les composantes actives. La méthode repose sur l'identification d'arbres couvrants communs aux deux graphes. Une méthode alternative pour étendre l'approche classique qui ne nécessite qu'un seul graphe a été proposée par Chen en 1965[note 5]. La méthode de Chen se base sur un arbre enraciné[46].
Hypergraphes
Une autre façon d'étendre la théorie classique des graphes pour les composantes actives consiste à utiliser des hypergraphes. Les graphes ne peuvent représenter simplement certaines composantes électroniques. Le transistor a trois points de connexion, mais une maille de graphe normale ne peut se connecter qu'à deux nœuds. Les circuits intégrés modernes ont encore plus de connexions. Ce problème peut être résolu en utilisant des hypergraphes au lieu des graphes ordinaires[48].
Dans une représentation conventionnelle, les composantes sont représentées par des arêtes, où chacune se connecte à deux nœuds. Dans un hypergraphe, les composantes sont représentées par des hyper-arêtes pouvant se connecter à un nombre arbitraire de nœuds. Les hyper-arêtes ont des tentacules reliant l'hyper-arête aux nœuds. La représentation graphique d'une hyper-arête peut être une boîte (en comparaison avec l'arête, qui est une ligne). Les représentations de ses tentacules sont des lignes de la boîte aux nœuds connectés. Dans un hypergraphe dirigé, les tentacules portent des étiquettes déterminées par l'étiquette de l'hyper-arête. Un graphe dirigé conventionnel peut être considéré comme un hypergraphe avec des hyper-arêtes dont chacune a deux tentacules. Ces deux tentacules sont étiquetés source et cible. Ils sont généralement indiqués par une flèche. Dans un hypergraphe général avec plus de tentacules, un étiquetage plus complexe sera nécessaire[49].
On peut caractériser les hypergraphes par leurs matrices d'incidence. Un graphe régulier contenant uniquement des composantes à deux terminaux aura exactement deux entrées non nulles dans chaque ligne de la matrice. Toute matrice d'incidence ayant plus de deux entrées non nulles dans une ligne est une représentation d'un hypergraphe. Le nombre d'entrées non nulles consécutives est le rang de la maille correspondante alors que le rang de la maille le plus élevé est le rang de la matrice d'incidence[50].
Variables non homogènes
L'analyse de réseau classique présente un ensemble d'équations de réseau dont les variables sont homogènes soit en courant (analyse des boucles), soit en tension (analyse des nœuds). L'ensemble des variables du réseau ainsi trouvé ne constitue pas forcément le minimum nécessaire pour former un ensemble d'équations indépendantes. Le nombre de variables peut différer entre une analyse de boucle et une analyse de nœud. Dans certains cas, le nombre minimal possible peut être encore inférieur si l'on assouplit l'exigence d'homogénéité et que l'on autorise ainsi un mélange de variables de courant et de variables de tension. Kishi et Katajini ont démontré en 1967 [note 6] que le nombre minimal absolu de variables nécessaires pour décrire le comportement du réseau est donné par la distance maximale [note 7] entre deux forêts couvrantes [note 8] du graphe du réseau[46].
Synthèse de réseau
On peut appliquer la théorie des graphes à la synthèse de réseaux. La synthèse de réseau classique réalise le réseau requis sous une forme canonique. Les formes canoniques existent d'ailleurs en grand nombre. Parmi les exemples de formes canoniques, on trouve la réalisation d'une impédance au point de conduite par le réseau d'échelles canoniques de Cauer, la forme canonique de Foster ou la réalisation par Brune d'une immittance à partir de ses fonctions positives-réelles. Les méthodes topologiques, en revanche, ne partent pas d'une forme canonique donnée. La forme est plutôt le résultat de la représentation mathématique. Certaines formes canoniques nécessitent des inductances mutuelles pour leur réalisation. Éliminer la nécessité de ces inductances mutuelles a constitué un objectif majeur des méthodes topologiques de synthèse de réseau. Un théorème issu de la topologie énonce que la réalisation d'une impédance de point d'attaque sans couplage mutuel est minimale si et seulement s'il n'y a aucune boucle contenant uniquement soit des inducteurs, soit des condensateurs[51].
La théorie des graphes est à son plus puissant dans la synthèse de réseaux dans deux cas. Le premier est lorsque les éléments du réseau peuvent être représentés par des nombres réels, comme dans les réseaux à un élément tels les réseaux résistifs. Le deuxième est rencontré dans les états binaires tels les réseaux de commutation[46].
Réseaux infinis
Le premier réseau avec un graphe infini à être étudié fut peut-être le réseau en échelle représentant les lignes de transmission que Heaviside développa dans sa forme finale en 1881. Sans doute que toutes les études initiales sur les réseaux infinis furent limitées à des structures périodiques telles que des échelles ou des grilles où on répétait les mêmes éléments à l'infini. Ce n'est qu'à la fin du XXe siècle que des outils d'analyse des réseaux infinis à topologie arbitraire devinrent disponibles[52].
Les réseaux infinis sont principalement d'un intérêt théorique amusant les mathématiciens. Les réseaux infinis dépourvus de restrictions dans le monde réel peuvent posséder des propriétés pas du tout physiques. Par exemple, les lois de Kirchhoff peuvent échouer dans certains cas. Des échelles de résistance infinies peuvent être définies ayant une impédance de point d'attaque dépendant de la terminaison à un point à l'infini. Une autre propriété non physique des réseaux infinis théoriques est qu'ils dissiperont généralement une puissance infinie, à moins qu'on leur impose des contraintes s'ajoutant aux lois habituelles, telles que les lois d'Ohm et de Kirchhoff. Des applications réelles existent néanmoins. L'exemple de la ligne de transmission fait partie d'une classe de problèmes pratiques qu'on peut modéliser par des éléments infinitésimaux (le modèle à éléments distribués). Des exemples supplémentaires sont le lancement d'ondes dans un milieu continu, les problèmes de champ de franges et la mesure de la résistance entre les points d'un substrat ou dans un trou de forage[53].
Les réseaux transfinis étendent l'idée des réseaux infinis encore davantage. Un nœud à une extrémité d'un réseau infini peut se connecter à une autre maille menant à un autre réseau. Ce nouveau réseau peut lui-même être infini. Des topologies peuvent ainsi être construites ayant des paires de nœuds sans chemin fini entre eux. De tels réseaux de réseaux infinis se nomment réseaux transfinis[54].
Remarques
- Yoke-chains. A terminology coined by Arthur Cayley. Yokes are branches in parallel, chains are branches in series.(MacMahon, 1891, p.330) A single branch can be considered either a yoke or a chain.
- Tie set. The term tie set was coined by Ernst Guillemin (Guillemin, p.xv). Guillemin says the name was chosen because if the branches of the tie set were reduced to zero length the graph would become "tied off" as a fishnet with a drawstring (Guillemin, p.17).
Guillemin was a leading figure in the development and teaching of linear network analysis (Wildes and Lindgren, pp.154–159). - Mesh. A mesh is a loop which does not enclose any other loops.
- Maze. This term is another coining by Guillemin (Guillemin, p.xv). So named because the spaces in a graph traversed by passing through the links has the form of a puzzle maze.
- Chen, Wai-Kai., "Topological analysis for active networks", IEEE Transactions on Circuit Theory, vol.13, iss.4, pp.438–439, December 1966.
- A summary of this work was first presented at;
- Distance between trees is defined as the number of edges that are in one tree but not in the other. That is, it is the number of edges which must be changed in order to transform one tree into the other (Kishi and Kajitani, p.323).
- Spanning forest. A forest of trees in which every node of the graph is visited by one of the trees.
Voir également
Références
- Tooley, pp. 258–264
- Guillemin, pp.5–6
- MacMahon (1891), p.331
- Farago, pp.18–21
Redifon, p.22 - Redifon, p.22
- Farago, pp.112–116
Redifon, pp.45–48 - Farago, pp.117–118
- Farago, pp. 125–127
- Campbell, pp.5–6, Kind and Fesser, pp.29–30
- Campbell, pp.5–6, 20
- Farago, pp. 98–134
- Suresh, pp.483–484, 530–532
- Kirchhoff, G. (1847) "Über die Auflösung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Ströme geführt wird" (On the solution of the equations to which one is led during the investigation of the linear distribution of galvanic currents), Annalen der Physik und Chemie, 72 (12) : 497–508.
- James Clerk Maxwell, A Treatise on Electricity and Magnetism (Oxford, England: Clarendon Press, 1873), vol. 1, Part II, "On linear systems of conductors in general", pp. 333–336.
- Wataru Mayeda and Sundaram Seshu (November 1957) "Topological Formulas for Network Functions," University of Illinois Engineering Experiment Station Bulletin, no. 446, p. 5.
- H. Poincaré (1900) "Second complément à l'Analysis Situs", Proceedings of the London Mathematical Society, 32 : 277–308. Available on-line at: Mocavo.com
- Oswald Veblen, The Cambridge Colloquium 1916, (New York : American Mathematical Society, 1918-1922), vol 5, pt. 2 : Analysis Situs, "Matrices of orientation", pp. 25-27.
- Cederbaum, p.64
- Foster, p.309
Foster and Campbell, p.232 - Guillemin, p.5
- Guillemin, pp.5–6
Suresh, p.485 - Guillemin, p.5
Minas, pp.213–214
Suresh, p.485 - Suresh, pp.485, 487–489
- Foster, p.310
- Guillemin, p.6-7
Foster, p.310 - Guillemin, p. 7
Suresh, p. 486 - Guillemin, pp.8–9
- Guillemin, pp.9–10
- Guillemin, pp.10–17
- Guillemin, pp.23–27
Suresh p.514 - Guillemin, pp.17–23
- Guillemin, p.43
Suresh, p.518, pp.523–528 - Foster, pp.310–311
- Foster, pp.312–313
- Guillemin, pp.64–81
- Guillemin, pp.112–116
- Guillemin, pp.116–120
- Guillemin, p.44
Suresh, pp.516–517 - Guillemin, pp.49–50
Suresh, p.517 - Guillemin, pp.43–44
Foster, p.313 - Guillemin, pp.51–53
- Guillemin, p.535
Suresh, p.517 - Guillemin, p.536
- Guillemin, pp. 127–132
- Guillemin, pp.6–7
- Cederbaum, p.65
- Samuel J. Mason (September 1953) "Feedback theory — Some properties of signal flow graphs," Proceedings of the I.R.E., 41 (9) : 1144–1156.
- Minas, p.213
- Minas, pp.213–214
- Skiena, p.382
- Cederbaum, p.67
- Brittain, p.39
Zemanian, p.vii - Zemanian, pp.vii-ix, 17–18, 24–26
- Zemanian, p.x
Bibliographie
- Brittain, James E., The introduction of the loading coil: George A. Campbell and Michael I. Pupin ", Technology and Culture, vol. 11, no. 1, pp. 36-57, The Johns Hopkins University Press, DOI 10.2307/3102809 .
- Campbell, GA, "Théorie physique du filtre à ondes électriques", Bell System Technical Journal, , vol. 1, non. 2, pp. 1–32.
- Cederbaum, I., "Certaines applications de la théorie des graphes à l' analyse du réseau et la synthèse", IEEE Transactions sur les circuits et systèmes, vol.31, iss.1, pp. 64–68, .
- Farago, PS, An Introduction to Linear Network Analysis, The English Universities Press Ltd, 1961.
- Foster, Ronald M., "Circuits géométriques des réseaux électriques", Transactions de l'American Institute of Electrical Engineers, vol.51, iss.2, pp. 309-317, .
- Foster, Ronald M .; Campbell, George A., "réseaux de sortie maximum pour poste téléphonique et circuits de répéteurs", Transactions de l'American Institute of Electrical Engineers, Vol.39, iss.1, pp. 230-290, .
- Guillemin, Ernst A., Théorie du circuit d'introduction, New York: John Wiley & Sons, 1953 (OCLC 535111)
- Kind, Dieter; Feser, Kurt, Techniques d'essai à haute tension, traducteur Y. Narayana Rao, Newnes, 2001 (ISBN 0-7506-5183-0) .
- Kishi, Genya; Kajitani, Yoji, "arbres éloignés et maximalement partition principale d'un graphique linéaire", IEEE Transactions on Théorie des circuits, vol.16, iss.3, pp. 323-330, .
- MacMahon, Percy A., "Chaînes de joug et compositions multipartites en rapport avec les formes analytiques appelées" Arbres "", Actes de la London Mathematical Society, vol . 22 (1891), pp. 330–346 DOI 10.1112/plms/s1-22.1.330 .
- MacMahon, Percy A., "Combinaisons de résistances", The Electrician, vol.28, pp. 601–602, .
<br/> Réimprimé dans Discrete Applied Mathematics, vol.54, iss. Iss.2–3, pp. 225-228, DOI 10.1016/0166-218X(94)90024-8 .
- Minas, M., "Création de représentations sémantiques des diagrammes", Applications des transformations de graphes à la pertinence industrielle: atelier international, AGTIVE'99, Kerkrade, Pays-Bas, 1er-: actes, pp. 209-224, Springer, 2000 (ISBN 3-540-67658-9) .
- Journal radio de Redifon, 1970, William Collins Sons & Co, 1969.
- Skiena, Steven S., The Algorithm Design Manual, Springer, 2008, (ISBN 1-84800-069-3) .
- Suresh, Kumar KS, «Introduction to network topology» chapitre 11 in Electric Circuits And Networks, Pearson Education India, 2010 (ISBN 81-317-5511-8) .
- Tooley, Mike, BTEC First Engineering: Unités obligatoires et sélectionnées en option pour les premières BTEC en ingénierie, Routledge, 2010 (ISBN 1-85617-685-1) .
- Wildes, Karl L .; Lindgren, Nilo A., "Analyse et synthèse de réseaux: Ernst A. Guillemin", Un siècle d'ingénierie électrique et d'informatique au MIT, 1882–1982, pp. 154–159, MIT Press, 1985 (ISBN 0-262-23119-0) .
- Zemanian, Armen H., Infinite Electrical Networks, Cambridge University Press, 1991 (ISBN 0-521-40153-4) .




