Introduction à la mécanique quantique

Travail à chaud du métal : l'éclat jaune-orangé résulte du rayonnement thermique émis par la haute température de l'objet. Les autres pièces émettent aussi des rayonnements mais à fréquences trop petites pour l'œil humain. Une caméra infrarouge pourrait les montrer.

Le rayonnement thermique émis par la surface d'un objet est un rayonnement électromagnétique dû à son énergie interne. Si un objet est suffisamment chauffé, il commence à émettre de la lumière du côté rouge du spectre visible.

Si on continue à le chauffer, il passera du rouge au jaune, puis au blanc et au bleu au fur et à mesure que la fréquence de la lumière émise augmente. Un objet parfait est aussi bon émetteur qu'absorbeur : froid il sera parfaitement noir parce qu'il absorbera tout rayonnement et n'en émettra aucun. Ainsi, un objet thermique idéal est appelé « corps noir », et le rayonnement correspondant « rayonnement du corps noir ».

À la fin du XIX^e siècle, le rayonnement thermique était bien défini. Pourtant, la physique classique qui avait abouti à la loi de Rayleigh-Jeans et décrivait bien les résultats expérimentaux aux fréquences faibles, était incohérente pour les fréquences hautes (voir schéma ci-contre). Les physiciens ont alors cherché une théorie globale qui expliquerait tous les phénomènes observés.

Prédictions sur les quantités de rayonnement thermique selon les fréquences émises par un corps. En vert, les valeurs correctes données par la loi de Planck ; en rouge, les valeurs classiques données par la loi de Rayleigh-Jeans ; en bleu, l'approximation de Wien.

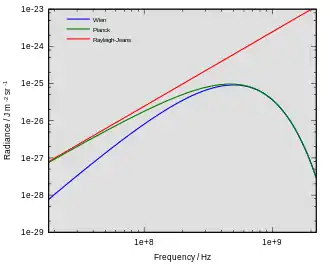
Le premier modèle qui permettait de décrire le spectre des rayonnements thermiques a été proposé par Max Planck en 1900[3]. Dans son modèle mathématique, le rayonnement thermique était en équilibre avec un ensemble d'oscillateurs harmoniques. Pour reproduire les résultats expérimentaux, il devait supposer que chaque oscillateur produisait un nombre entier d'unités d'énergie pour sa fréquence caractéristique, plutôt que d'émettre une quantité arbitraire. En d'autres termes, l'énergie de chaque oscillateur était « quantifiée ». Le quantum d'énergie de chaque oscillateur était, selon Planck, proportionnel à la fréquence de l'oscillateur ; ce coefficient de proportionnalité est maintenant connu sous le nom de constante de Planck.

La constante de Planck, notée h, vaut environ 6,63 × 10⁻³⁴ J s. Ainsi, l'énergie E d'un oscillateur de fréquence f est donnée par :

${\displaystyle E=nhf,\quad {\text{où}}\quad n=1,2,3,\ldots }$[4]

Pour changer la couleur d'un tel objet rayonnant, il faut modifier sa température. La loi de Planck, établissant une relation directe - une loi de puissance - entre la température d'un corps et l'énergie rayonnée, explique pourquoi : l'augmentation de la température d'un corps lui permet d'émettre plus d'énergie, ce qui entraîne une plus grande proportion d'énergie émise du côté violet du spectre.

La loi de Planck a été la première théorie quantique, et Planck a obtenu le prix Nobel en 1918 « en reconnaissance des services rendus et des progrès de la physique dus à sa découverte des quanta d'énergie »[5]. À cette époque, Planck pensait que la quantification n'était qu'une construction purement mathématique, alors qu'elle est maintenant considérée comme un changement fondamental dans notre compréhension du monde[6].

Albert Einstein vers 1905.

En 1905, Albert Einstein fait un pas en avant. Il suggère que la quantification n'est pas une simple construction mathématique, mais que l'énergie d'un faisceau lumineux est réellement découpée en paquets, qu'on appelle maintenant les photons. L'énergie d'un photon est donnée par sa fréquence multipliée par la constante de Planck :

${\displaystyle E=hf}$

Pendant des siècles, les scientifiques ont débattu entre deux théories possibles pour la lumière : était-ce une onde ou plutôt un flux de petites particules ? Au XIX^e siècle, le débat semblait avoir été réglé en faveur de la théorie ondulatoire, vu qu'elle expliquait les comportements observés tels que la réfraction, la diffraction, l’interférence et la polarisation. James Clerk Maxwell avait montré que l'électricité, le magnétisme et la lumière avaient pour origine le même phénomène : le champ électromagnétique. Les équations de Maxwell, qui forment l'ensemble des lois de l'électromagnétisme classique, décrivent la lumière comme une onde : une combinaison oscillatoire de champs, électrique et magnétique. Du fait de la prépondérance de preuves en faveur de la théorie ondulatoire, les idées d'Einstein ont été accueillies avec un grand scepticisme. Puis, finalement, le modèle des photons a pris le dessus. Une des preuves les plus importantes en sa faveur était sa capacité à expliquer plusieurs propriétés intrigantes de l'effet photoélectrique, décrit ci-dessous. Cependant, l'analogie avec les ondes restait valide pour comprendre les autres caractéristiques de la lumière telles que la diffraction, la réfraction et l'interférence.

L'effet photoélectrique

La lumière rayonne sur un métal. Si la lumière a une fréquence suffisante (elle contient suffisamment d'énergie), des électrons sont éjectés.

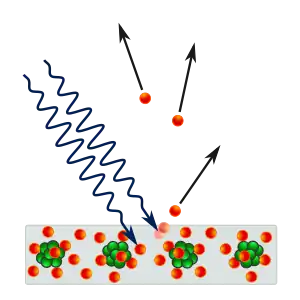
En 1887, Heinrich Hertz a observé que lorsque la lumière touchait une surface métallique avec une fréquence suffisante, elle émettait un électron. En 1902, Philipp Lenard a découvert que l'énergie maximale possible d'un électron éjecté était liée à la fréquence de la lumière et non à son intensité : si la fréquence est trop basse, aucun électron n'est éjecté, quelle que soit l'intensité. Ainsi, de forts faisceaux lumineux qui se trouvent du côté rouge du spectre peuvent ne produire aucun potentiel électrique, alors que de faibles faisceaux émis vers le côté violet du spectre peuvent produire des courants très forts. La plus basse fréquence de lumière qui provoque l'émission d'un électron, appelée « fréquence seuil », est différente pour chaque métal. Cette observation va à l'encontre de l'électromagnétisme classique qui prédit que l'énergie de l'électron doit être proportionnelle à l'intensité du rayonnement. Lorsque les physiciens ont étudié les premiers dispositifs utilisant l'effet photoélectrique, ils s'attendaient à ce qu'une plus grande intensité de lumière produise un plus grand courant dans le dispositif.

Einstein a expliqué cet effet en postulant qu'un faisceau lumineux est composé de particules (les photons), et que, si le faisceau a une fréquence f, alors chaque photon a une énergie égale à hf. Un électron a une forte probabilité d'être percuté par un seul photon, ce qui communique à cet électron une énergie valant au plus hf. En conséquence, l'intensité du faisceau électrique n'a aucun effet et seule sa fréquence détermine l'énergie maximale qui peut être communiquée à un électron.

Pour expliquer l'effet de seuil, Einstein a affirmé qu'une certaine quantité d'énergie était nécessaire, appelée « travail de sortie » et notée φ, pour extraire un électron du métal. Cette quantité d'énergie diffère pour chaque métal. Si l'énergie du photon est inférieure au travail de sortie, alors il ne possède pas assez d'énergie pour faire sortir l'électron du métal. La fréquence seuil, f₀, est la fréquence d'un photon dont l'énergie est égale au travail de sortie :

${\displaystyle \varphi =hf_{0}.}$

Si f est supérieure à f₀, l'énergie hf est suffisante pour extraire un électron. L'électron éjecté a une énergie cinétique E_K, qui est au plus égale à l'énergie du photon moins l'énergie nécessaire pour extraire l'électron du métal :

${\displaystyle E_{K}=hf-\varphi =h(f-f_{0}).}$

La description de la lumière, composée de particules, faite par Einstein a étendu la notion d'énergie quantifiée de Planck : elle énonce qu'un photon ayant une fréquence donnée f, transporte une quantité d'énergie invariante hf. En d'autres termes, un photon peut transporter plus ou moins d'énergie, mais elle dépendra uniquement de sa fréquence. Dans la nature, on rencontre rarement des photons seuls. Le Soleil et les autres sources disponibles au XIX^e siècle émettent un grand nombre de photons chaque seconde ; l'importance de l'énergie transportée par chaque photon n'était donc pas évidente. L'idée d'Einstein que l'énergie contenue dans une unité de lumière dépend de sa fréquence a permis d'expliquer des résultats expérimentaux qui semblaient jusqu'ici paradoxaux. Cependant, bien que le photon soit une particule, il continuait à être décrit par une propriété ondulatoire : sa fréquence. Une fois de plus, l'état corpusculaire de la lumière était discrédité.

À l'aube du XX^e siècle, les preuves expérimentales esquissent un modèle atomique composé d'un nuage diffus d'électrons, chargés négativement, entourant un petit noyau dense, chargé positivement. Ces propriétés suggèrent un modèle dans lequel les électrons tournent autour du noyau comme les planètes autour du Soleil (en fait les orbites ne sont pas planes comme pour les planètes mais parcourent toute la sphère enveloppant le noyau). Toutefois, on sait qu'un atome suivant ce modèle serait instable : selon la théorie classique, les électrons en orbite subissent une accélération centripète qui devrait leur faire émettre un rayonnement électromagnétique, cette perte d'énergie les poussant aussi vers le noyau, ils finiraient par s'y écraser en une fraction de seconde.

Une deuxième énigme, liée à la première, concernait le spectre d'émission. Quand un gaz est chauffé, il émet de la lumière uniquement dans quelques fréquences discrètes. Par exemple, la lumière visible émise par l'hydrogène est composée de quatre couleurs distinctes, affichées dans l'image ci-dessous. Aussi, l'intensité de la lumière est différente pour chaque fréquence. En comparaison, la lumière blanche est composée d'une émission continue à travers tout le spectre des fréquences visibles. À la fin du XIX^e siècle, une règle simple connue sous le nom de série de Balmer a été découverte, qui fournit une relation entre les fréquences des différentes raies, mais sans expliquer pourquoi elles prennent ces valeurs, et sans même faire aucune prédiction sur leurs intensités. Cette formule prédisait quelques raies spectrales supplémentaires situées dans l'ultraviolet et l'infrarouge qui n'avaient jamais été observées à cette époque. Ces raies seront observées expérimentalement plus tard, renforçant la confiance en cette formule.

Spectre d'émission de l'hydrogène. Quand il est excité, l'atome d'hydrogène émet de la lumière dans quatre couleurs différentes (raies spectrales) du spectre visible, ainsi que plusieurs autres raies dans l'infrarouge et l'ultraviolet.

Le modèle de Bohr pour un atome, montrant la transition d'un électron d'une orbite à une autre en émettant un photon.

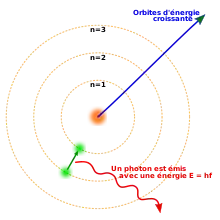
En 1913, Niels Bohr a proposé un nouveau modèle atomique qui représentait des orbites électroniques quantifiées : les électrons continuent à tourner autour du noyau comme les planètes autour du Soleil, mais ils ne peuvent occuper que certaines orbites. Quand un atome émet ou absorbe de l'énergie, l'électron ne se déplace pas selon une trajectoire continue d'une orbite à une autre, comme on pourrait s'y attendre selon la physique classique. À la place, l'électron saute instantanément d'une orbite à l'autre - phénomène de recombinaison par cascade -, émettant de la lumière sous forme d'un photon. Les énergies possibles des photons émis par chaque élément sont déterminées par la différence d'énergie entre deux orbites - différence de niveaux - , ainsi le spectre d'émission pour chaque élément contient un nombre déterminé de raies.

Niels Bohr jeune

En partant d'une simple supposition sur les règles régissant les orbites, le modèle de Bohr était capable de lier les raies spectrales observées dans le spectre d'émission de l'hydrogène à des constantes déjà connues. Le modèle de Bohr interdisait juste à l'électron d'émettre de l'énergie continuellement et de s'écraser sur le noyau : une fois installé sur l'orbite la plus proche du noyau, il était définitivement stable. Le modèle de Bohr n'expliquait pas pourquoi les orbites étaient quantifiées de cette façon, il ne permettait pas non plus de faire des prédictions précises pour les atomes ayant plusieurs électrons, et ne disait même pas pourquoi certaines raies spectrales étaient plus brillantes que d'autres.

Bien que les hypothèses fondamentales du modèle de Bohr allaient être réfutées, le résultat principal énonçant que les raies du spectre d'émission sont liées à des propriétés des atomes quantifiant les orbites des électrons reste correct. En effet, le comportement réel des électrons est radicalement différent de la description faite par le modèle de Bohr, et de ce que l'on observe dans l'expérience de tous les jours ; le modèle moderne de l'atome dans la mécanique quantique est discuté ci-dessous.

Louis de Broglie en 1929. De Broglie a obtenu le prix Nobel de physique pour sa prédiction du comportement ondulatoire de la matière, faite dans sa thèse de 1924.

De la même façon que la lumière se comporte à la fois comme une onde et comme une particule, cette spécificité est aussi valable pour la matière.

Le comportement ondulatoire de la matière a été d'abord démontré expérimentalement pour l'électron : un faisceau d'électrons est capable de diffraction tout comme un faisceau de lumière ou une vague dans l'eau. De la même manière, des phénomènes ondulatoires seront démontrés plus tard pour des atomes et même de petites molécules.

La longueur d'onde λ, associée à tout objet, est liée à sa quantité de mouvement p par la constante de Planck h :

${\displaystyle p={\frac {h}{\lambda }}.}$

Cette formule, connue sous le nom d'hypothèse de De Broglie, est valable pour tout type de matière : toute la matière possède à la fois les propriétés d'onde et de particule.

Le concept de dualité onde-corpuscule énonce qu'aucun des concepts classiques, qu'ils décrivent une particule ou une onde, ne peut expliquer à eux seuls tous les comportements des objets à l'échelle quantique, que ce soient des photons ou de la matière. La dualité onde-corpuscule est un exemple du principe de complémentarité en physique quantique. Un exemple intéressant de cette dualité est l'expérience des fentes de Young, expliquée ci-dessous.

En haut : motif de diffraction produit par la lumière qui passe à travers une seule fente ; en bas : motif d'interférence produit par deux fentes proches. Le motif bien plus complexe produit par les deux fentes, qui forme des franges d'interférence à petite échelle, démontre la propagation ondulatoire de la lumière.

Dans l'expérience des fentes de Young, réalisée pour la première fois par Thomas Young et Augustin Fresnel en 1827, un faisceau de lumière est dirigé vers deux petites fentes rapprochées et produit des franges d'interférence sur un écran sous forme de bandes claires et obscures. Si l'une des fentes est fermée, on pourrait s'attendre à ce que l'intensité des franges dues à l'interférence soit diminuée de moitié. En réalité, c'est une figure beaucoup plus simple qui apparaît: une ligne de diffraction. Ainsi, la fermeture d'une fente donne une image plus simple en face de la fente ouverte. Un comportement identique peut être observé avec des vagues dans l'eau, l'expérience de Young était donc vue comme une démonstration de la nature ondulatoire de la lumière.

L'expérience de Young a été aussi vérifiée avec des électrons, des atomes, et même des molécules, et l'on observe à chaque fois les mêmes figures d'interférence. Ainsi, Il a été démontré que toute la matière possède à la fois les propriétés d'une onde et d'une particule.

Même en réduisant l'intensité de la source, jusqu'à ce qu'une seule particule passe par la fente (un photon ou un électron), les mêmes motifs sont toujours reproduits. La particule quantique se comporte comme une onde quand elle passe à travers les deux fentes, mais comme une particule lorsqu'elle est détectée (par un appareil qui « regarde » dans quelle fente elle passe). C'est une propriété typique de la complémentarité quantique : une particule quantique va agir comme une onde dans une expérience qui mesure ses propriétés ondulatoires, et comme une particule dans une expérience qui mesure ses propriétés corpusculaires. Le point qui s'affiche sur l'écran de détection, correspondant à une particule seule, sera le résultat du hasard. Cependant, le motif obtenu par distribution d'un grand nombre de particules individuelles reproduira la ligne de diffraction créée par des vagues.

En 1922, Otto Stern et Walther Gerlach ont lancé des atomes d'argent à travers un champ magnétique (non homogène). En mécanique classique, un aimant lancé à travers un champ magnétique sera, selon son orientation (si son pôle correspondant au nord pointe vers le haut ou le bas, ou quelque part entre les deux), dévié d'une distance plus ou moins grande vers le haut ou vers le bas. Les atomes que Stern et Gerlach ont lancés à travers le champ magnétique se sont comportés d'une manière similaire. Sauf que là où les aimants étaient déviés sur des distances variables, les atomes étaient déviés sur une distance constante soit vers le haut soit vers le bas. Cela impliquait que la propriété des atomes correspondant à l'orientation des aimants devait être quantifiée, prenant une valeur parmi deux possibles (haut ou bas, en anglais up ou down), aucun autre angle d'orientation n'étant admis.

Ralph Kronig a eu l'idée selon laquelle les particules telles que les atomes ou les électrons se comportaient comme si elles tournaient à la manière d'une girouette (en anglais spin) autour d'un axe. Le spin pouvait alors remplir le rôle du moment magnétique et permettre à deux électrons d'occuper la même orbite atomique en satisfaisant le principe d'exclusion de Pauli, ayant des spins opposés.

Le choix de l'orientation du champ magnétique utilisé dans l'expérience de Stern et Gerlach est arbitraire. Dans l'animation montrée ici, le champ est vertical et les atomes sont déviés soit vers le haut soit vers le bas. Si le champ est tourné d'un quart de tour, les atomes seront déviés soit à gauche soit à droite. Le spin est donc quantifié selon l'axe du champ.

Si, à la place de l'écran de détection situé à la sortie de l'expérience de Stern et Gerlach, l'un des faisceaux d'atomes est envoyé vers un autre champ magnétique (non homogène) orienté dans la même direction, tous les atomes seront déviés de la même façon dans le deuxième champ. Par contre, si le deuxième champ est tourné de 90° par rapport au premier, alors la moitié des atomes seront déviés d'un côté, ainsi le spin des atomes selon l'axe horizontal et vertical est indépendant. Cependant, si l'un des faisceaux (par exemple celui qui a été dévié en haut puis à gauche) passe à travers un troisième champ magnétique orienté comme le premier, alors les atomes seront encore séparés en deux moitiés. L'action de mesure du spin des atomes par le champ horizontal a modifié leur spin par rapport au champ vertical.

L'expérience de Stern et Gerlach démontre plusieurs résultats importants en mécanique quantique :

• Notre monde naturel est quantifié, et ne peut prendre que certaines valeurs discrètes
• Les particules possèdent un moment cinétique intrinsèque qui ressemble beaucoup au moment angulaire d'un objet en rotation dans la mécanique classique
• En mécanique quantique, la mesure d'un système le modifie. Le spin d'un objet ne peut être connu que dans une direction, et observer ce spin dans une autre direction va détruire l'information du spin originel.
• La mécanique quantique est probabiliste : la valeur du spin d'un atome envoyé dans l'appareil, positive ou négative, est aléatoire.

En 1925, Werner Heisenberg a essayé de comprendre un des problèmes posés par le modèle de Bohr : les différences d'intensités découvertes dans les raies spectrales de l'atome d'hydrogène. En utilisant une série d'analogies mathématiques, il a écrit un équivalent quantique du calcul des intensités de la mécanique classique. Peu après, Max Born, un collègue de Heisenberg, s'est aperçu que la méthode utilisée par Heisenberg pour calculer les probabilités des transitions entre les différents niveaux d'énergie pouvaient être mieux décrite avec le concept mathématique de matrice.

La même année, en se basant sur l'hypothèse de De Broglie, Erwin Schrödinger a développé l'équation qui décrit le comportement d'une onde en mécanique quantique. Ce modèle mathématique, appelé « équation de Schrödinger » d'après son créateur, qui est un élément central de la mécanique classique, définit les états stables autorisés pour un système quantique, et décrit comment les états quantiques changent dans le temps. L'onde elle-même est décrite par une fonction mathématique connue sous le nom de « fonction d'onde ». Schrödinger a expliqué que la fonction d'onde permettait de prédire la probabilité des résultats des mesures.

Schrödinger a réussi à calculer l'énergie des niveaux de l'hydrogène en considérant l'électron de l'atome d'hydrogène comme une onde classique se déplaçant dans un puits de potentiel électrique créé par le proton. Ce calcul a précisément reproduit les niveaux d'énergie du modèle de Bohr.

En mai 1926, Schrödinger a prouvé que la mécanique matricielle de Heisenberg et sa propre méthode de calcul faisaient les mêmes prédictions sur les propriétés et le comportement de l'électron ; mathématiquement, les deux théories avaient une forme sous-jacente commune. Pourtant les deux hommes n'étaient pas d'accord sur l'interprétation de leurs théories respectives. Par exemple Heisenberg, acceptait la prédiction théorique du saut des électrons entre les orbites d'un atome, mais Schrödinger espérait qu'une théorie fondée sur des propriétés continues similaires à une onde pourraient éviter ce qu'il appelait « cette absurdité des sauts quantiques » (propos rapportés par Wilhelm Wien).

Bohr, Heisenberg et bien d'autres ont essayé d'expliquer ce que ces résultats d'expériences et ces modèles mathématiques signifiaient réellement. Leur description, connue sous le nom d' « interprétation de Copenhague de la mécanique quantique », avait pour but de décrire la nature de la réalité telle qu'observée par les mesures et représentée par les formulations mathématiques de la mécanique quantique.

Les grands principes de l'interprétation de Copenhague sont :

1. Un système est entièrement décrit par une fonction d'onde, en général notée par la lettre grecque ${\displaystyle \psi }$ (psi). (Heisenberg)
2. Les évolutions de ${\displaystyle \psi }$ dans le temps sont données par l'équation de Schrödinger.
3. La description de la nature est essentiellement probabiliste. La probabilité d'un événement, par exemple, quand une particule apparaît sur l'écran de détection dans l'expérience des fentes de Young, est fonction du carré de la valeur absolue de l'amplitude de sa fonction d'onde (la règle de Born, du physicien Max Born, donne une signification physique à la fonction d'onde dans l'interprétation de Copenhague : l'amplitude de probabilité).
4. Il n'est pas possible de connaître les valeurs de toutes les propriétés du système au même moment ; les propriétés qui ne sont pas connues avec précision doivent être décrites par des probabilités (principe d'incertitude de Heisenberg).
5. La matière, comme l'énergie, possède une dualité onde-corpuscule. Une expérience peut démontrer l'état corpusculaire de la matière ou ses propriétés ondulatoires, mais pas les deux à la fois (principe de complémentarité dû à Bohr).
6. Les appareils de mesure sont des appareils classiques par nature, et mesurent donc des propriétés classiques telles que la position et la quantité de mouvement.
7. La description quantique de grands systèmes est proche de leur description classique (principe de correspondance de Bohr et Heisenberg).

Les diverses conséquences de ces principes sont discutées dans les sections suivantes.

Principe d'incertitude

Le principe d'incertitude de Heinsenberg devrait être nommé 'principe d'indétermination de Heinsenberg', ce qui correspond mieux au nom donné à ce principe par Heinsenberg lui-même et surtout permet de lever l'ambiguité liée à la question de la précision de la mesure dont il n'est pas question. Le nom principe d'incertitude est resté dans les usages, mais correspond mal à la compréhension qui doit être faite du comportement quantique des particules.

Werner Heisenberg à 26 ans. Heisenberg a obtenu le Prix Nobel de physique en 1932 pour le travail qu'il avait accompli à cette époque[7].

Supposons que l'on veuille mesurer la position et la vitesse d'un objet, par exemple une voiture qui traverse une zone surveillée par un radar. On peut considérer que cette voiture a une position et une vitesse bien définies à un moment donné dans le temps. La précision avec laquelle ces valeurs peuvent être mesurées dépend de la qualité de l'équipement de mesure ; si la précision de l'équipement de mesure est améliorée, il donnera un résultat plus proche de la valeur réelle. En pratique, on peut supposer que la vitesse de la voiture et sa position peuvent être définies et mesurées simultanément, et aussi précisément qu'on le souhaite.

En 1927, Heisenberg a prouvé que cette dernière hypothèse était incorrecte. En mécanique quantique certains couples de propriétés physiques, tels que la position et la vitesse, ne peuvent être mesurés simultanément avec une précision arbitraire : plus la mesure de l'une des propriétés sera effectuée précisément, moins l'autre pourra être précise. Cette affirmation est connue sous le nom de principe d'incertitude. Le principe d'incertitude ne concerne pas la précision de nos équipements de mesure, mais, plus fondamentalement, la nature conceptuelle des quantités mesurées : l'hypothèse que l'on pouvait définir simultanément la position et la vitesse de la voiture ne marche pas en mécanique quantique. À l'échelle des voitures et des hommes, ces incertitudes sont négligeables, mais lorsque l'on travaille avec des atomes et des électrons elles deviennent critiques.

Heisenberg a donné comme démonstration la mesure de la position et de la quantité de mouvement d'un électron grâce à un photon de lumière. Pour mesurer la position de l'électron, plus la fréquence du photon est grande et plus la mesure de la position au moment de l'impact est précise, mais plus grande est la perturbation de l'électron qui absorbe une quantité d'énergie aléatoire : ceci introduit une incertitude d'autant plus grande sur sa quantité de mouvement (i.e. sa vitesse multipliée par sa masse), puisque l'on mesure nécessairement la quantité de mouvement du produit de la collision et pas celle de l'électron original qui a été perturbé. Avec un photon de fréquence plus faible, la perturbation de la quantité de mouvement (et donc l'incertitude) est aussi plus faible, mais il en est de même pour la précision de la mesure de la position de l'impact.

Le principe d'incertitude montre mathématiquement que le produit de l'incertitude dans la position et de la quantité de mouvement d'une particule ne peut jamais descendre en dessous d'une certaine valeur, et cette valeur est liée à la constante de Planck.

Principe d'exclusion de Pauli

Wolfgang Pauli

En 1924, Wolfgang Pauli a proposé un nouveau degré de liberté quantique (appelé nombre quantique), ayant deux valeurs possibles, pour résoudre les incohérences entre le spectre moléculaire observé et les prédictions de la mécanique quantique. En particulier, le spectre de l'atome d'hydrogène avait un doublet, c'est-à-dire une paire de raies très proches, là où une seule était attendue. Pauli a ainsi formulé son principe d'exclusion en disant qu' « il ne peut pas exister d'atome dont l'état quantique inclurait deux électrons ayant le même ensemble de nombres quantiques ».

Un an plus tard, George Uhlenbeck et Samuel Goudsmit ont identifié le nouveau degré de liberté de Pauli comme étant la propriété appelée spin dont les effets avaient été observés dans l'expérience de Stern et Gerlach.

Application à l'atome d'hydrogène

Le modèle atomique de Bohr ressemblait beaucoup à un système planétaire, avec les électrons en orbite autour du noyau « soleil ». Cependant, le principe d'incertitude spécifiait que l'on ne pouvait connaitre à la fois la position et la vitesse exactes d'un électron comme pour une planète. Au lieu d'orbites classiques, on dit que les électrons occupent des orbitales atomiques. Une orbitale représente le nuage des positions possibles dans lesquelles un électron peut être trouvé, c'est une distribution de probabilités plutôt qu'une position précise. Chaque orbitale est tridimensionnelle (en comparaison des orbites classiques qui sont en deux dimensions) et est généralement représentée par la région en trois dimensions dans laquelle on a 95 % de chances de trouver l'électron.

Schrödinger a réussi à calculer les niveaux d'énergie de l'hydrogène en considérant l'électron de cet atome comme une onde, représentée par la fonction d'onde ${\displaystyle \psi }$, dans un puits de potentiel électrique V créé par le proton. Les solutions à l'équation de Schrödinger sont des distributions de probabilités pour les positions de l'électron. Les orbitales possèdent un grand nombre de formes différentes en trois dimensions. L'énergie de chaque orbitale peut être calculée, et elles correspondent exactement aux niveaux d'énergie du modèle de Bohr.

Pour Schrödinger, l'électron a quatre propriétés :

1. un nom d'orbitale, indiquant si l'onde de la particule est proche du noyau avec peu d'énergie ou loin du noyau avec plus d'énergie ;
2. une forme d'orbitale, sphérique ou autre ;
3. une inclinaison de l'orbitale, déterminant le moment magnétique de l'orbitale autour de l'axe z
4. le spin de l'électron

L'ensemble de ces propriétés forme l'état quantique de l'électron. L'état quantique peut alors être décrit en donnant un numéro à chacune de ces propriétés : ils sont connus sous le nom de nombres quantiques.

Les formes des cinq premières orbitales atomiques : 1s, 2s, 2p_x, 2p_y, et 2p_z. Les couleurs montrent les phases de la fonction d'onde.

La première propriété décrivant l'orbitale est le nombre quantique principal, n, qui est le même que dans le modèle de Bohr. n décrit le niveau d'énergie de chaque orbitale. Les valeurs possibles pour n sont tous les entiers :

${\displaystyle n=1,2,3\ldots }$

Le nombre quantique suivant, appelé nombre quantique azimutal et noté l, décrit la forme de l'orbitale. La forme est une conséquence du moment cinétique de l'orbitale. Le moment cinétique représente la résistance à l'accélération ou au ralentissement, d'un objet qui tourne, sous l'influence d'une force extérieure. Le nombre quantique azimutal représente le moment cinétique de l'orbitale d'un électron autour de son noyau. Les valeurs possibles pour l sont les entiers de 0 à n-1 :

${\displaystyle l=0,1,\ldots ,n-1.}$

La forme des orbitales a aussi sa propre notation. La première est notée s (comme sphère). La suivante est notée p et a la forme d'un haltère. Les autres orbitales ont des formes plus compliquées et sont notées avec les lettres d, f et g.

Le troisième nombre quantique, le nombre quantique magnétique, décrit le moment magnétique de l'électron et se note m_l (ou tout simplement m). Les valeurs possibles pour m_l sont les entiers compris entre -l et l :

${\displaystyle m_{l}=-l,-(l-1),\ldots ,0,1,\ldots ,l.}$

Le nombre quantique magnétique mesure la composante du moment cinétique dans une direction donnée. Le choix de la direction est arbitraire, par convention on choisit l'axe z.

Le quatrième nombre quantique, le nombre quantique de spin (qui correspond à l'orientation du spin de l'électron) est noté m_s et ses valeurs sont comprises entre +¹⁄₂ ou −¹⁄₂.

Le chimiste Linus Pauling a écrit, à titre d'exemple :

« Dans le cas d'un atome d'hélium ayant deux électrons dans l'orbitale 1s, le principe d'exclusion de Pauli implique que les deux électrons diffèrent sur la valeur de l'un des nombres quantiques. Leurs valeurs de n, l et m_l sont identiques. Les valeurs doivent alors être différentes pour m_s, qui peut prendre la valeur +¹⁄₂ pour un électron et −¹⁄₂ pour l'autre. »

C'est la structure sous-jacente, la symétrie des orbitales et la façon dont les électrons les remplissent, qui mènent à l'organisation du tableau périodique des éléments. Aussi, la façon dont les orbitales atomiques des différents atomes se combinent pour former les orbitales moléculaires détermine la structure et la force des liens chimiques entre les atomes.

En 1928, Paul Dirac a modifié l'équation de Pauli, qui décrit la rotation des électrons, pour tenir compte de la relativité restreinte. Ce qui a donné une théorie décrivant correctement des événements tels que la vitesse d'un électron sur l'orbitale autour du noyau (égale à une fraction importante de la vitesse de la lumière). En utilisant simplement l'interaction électromagnétique, Dirac a pu prédire la valeur du moment magnétique associé au spin de l'électron, et retrouver la valeur observée expérimentalement, qui était trop grande pour être celle d'une sphère chargée en rotation gouvernée par la physique classique. Il a pu résoudre le problème des raies spectrales de l'atome d'hydrogène et reproduire à partir de principes physiques simples la formule de Sommerfeld pour la structure fine du spectre de l'hydrogène.

Les équations de Dirac donnent parfois une valeur négative pour l'énergie, il a alors proposé une solution originale : il a postulé l'existence d'un antiélectron et une dynamique du vide. Ce qui mena à la théorie quantique des champs.

Superposition de deux caractéristiques quantiques, et deux possibilités de résolution.

Le principe d'exclusion de Pauli énonce que deux électrons d'un même système ne peuvent être dans le même état. La nature laisse cependant la possibilité à deux électrons d'avoir des états « superposés ». Rappelez-vous que les fonctions d'onde qui sortent simultanément des deux fentes de Young atteignent l'écran de détection dans un état de superposition. On ne sait rien tant que les ondes superposées ne sont pas « réduites ». À cet instant, un électron apparaît dans une position dépendant de la probabilité équivalente au carré de la valeur absolue de la somme des deux amplitudes des ondes superposées.

Mais cet exemple reste abstrait. Pour expliquer d'une façon concrète l'état de deux photons intriqués, prenons deux photons dans des états contraires qui sont superposés l'un sur l'autre dans le même événement :

Imaginons que la superposition d'un état mentalement matérialisé en bleu et d'un autre état matérialisé en rouge, va apparaître (toujours mentalement) en un état violet. Deux photons sont produits par le même évènement atomique. Peut-être qu'ils sont produits par l'excitation d'un cristal dont la caractéristique est d'absorber un photon d'une fréquence donnée et d'émettre deux photons ayant la moitié de la fréquence originale. Ainsi les deux photons apparaissent en violet. Maintenant, si l'expérimentateur réalise une expérience pour déterminer si l'un des photons est bleu ou rouge, alors cette expérience va modifier le photon observé d'un état de superposition de deux caractéristiques, bleu et rouge, vers un photon qui n'a qu'une seule de ces deux caractéristiques. Le problème qu'a eu Einstein en imaginant une telle situation était que si l'un de ces photons était conservé dans un laboratoire sur Terre, rebondissant entre deux miroirs, et que l'autre était envoyé à mi-chemin vers l'étoile la plus proche, alors une fois que son jumeau serait forcé de révéler sa couleur (bleu ou rouge), le photon distant devrait lui aussi perdre son état violet. Ainsi, toute vérification effectuée après que son jumeau a été mesuré, devait nécessairement montrer un état opposé à ce que son jumeau avait dévoilé.

En essayant de démontrer que la mécanique quantique était une théorie incomplète, Einstein a commencé par la prédiction faite par la théorie que deux particules (ou plus) ayant interagi par le passé peuvent apparaître fortement corrélées lors de la mesure future de leurs propriétés. Il a essayé d'expliquer cette apparente interaction de manière classique, en utilisant leur passé commun, et de préférence sans « action surnaturelle à distance ». Cet argument a été développé dans un article célèbre d'Einstein, Podolsky et Rosen en 1935 (initiales EPR), énonçant ce qu'on connait aujourd'hui sous le nom de paradoxe EPR. En admettant que cette idée est maintenant appelée « réalisme local », l'article EPR essayait de montrer que dans la théorie quantique une particule avait à la fois une position et un moment cinétique, alors que dans l'interprétation de Copenhague, seule une et une seule de ces deux propriétés pouvait exister au moment où elle était mesurée. Ils ont conclu que la théorie quantique était incomplète et ont par conséquent refusé d'admettre des propriétés physiques qui existaient objectivement dans la nature. Cet article EPR de 1935 est la publication d'Einstein la plus citée dans les journaux de physique. La même année, Erwin Schrödinger a utilisé le mot anglais entanglement (« enchevêtrement » en français, traduit plutôt par « intrication ») et déclaré : « je ne considère pas cela comme une, mais comme la caractéristique de la mécanique quantique »[8]. La question de savoir si l'intrication est un état réel est toujours en discussion. Les inégalités de Bell représentent le plus grand défi aux affirmations d'Einstein.

L'idée d'une théorie quantique des champs a germé dans les années 1920 quand le physicien britannique Paul Dirac a essayé de quantifier le champ électromagnétique, qui est une façon de construire une théorie quantique en partant d'une théorie classique.

En physique, un champ est « une région de l'espace dans laquelle un effet donné (tel que le magnétisme) existe »[9]. D'autres effets qui se manifestent à travers des champs sont la gravitation et l'électricité statique. En 2008, le physicien Richard Hammond a écrit :

« Parfois on fait la distinction entre la mécanique quantique et la théorie quantique des champs. La première se réfère à un système dans lequel le nombre de particules est fixe et où les champs (tel le champ électromagnétique) sont des entités classiques continues. La seconde va un peu plus loin et permet la création et l'annihilation de particules... »

Il a cependant ajouté que la notion de « mécanique quantique » est souvent utilisée pour tout ce qui est quantique.

En 1931, Dirac a proposé l'existence de particules qui seront plus tard connues comme l'antimatière. Dirac a partagé le Prix Nobel de physique de 1933 avec Schrödinger, « pour la découverte de nouvelles formes productives de la théorie atomique » [10].

À première vue, la théorie quantique des champs autorise un nombre infini de particules, et laisse à la théorie le soin de prédire combien et avec quelles probabilités elles doivent exister. Si on continue à la développer, cette théorie contredit souvent l'observation, ce qui fait que seuls ses opérateurs de création d'annihilation peuvent être vérifiés expérimentalement. De plus, les lois empiriques de conservation, comme celle de l'équivalence masse énergie, imposent certaines contraintes sur la forme mathématique de la théorie, qui sont mathématiquement fastidieuses. Ce dernier élément rend les théories des champs difficiles à manipuler, mais a aussi mené à des restrictions supplémentaires sur les formes possibles de la théorie. Voir la partie sur la normalisation dans la section ci-dessous.

L'électrodynamique quantique est le nom de la théorie quantique de la force électromagnétique. Pour la comprendre il faut commencer par l'électromagnétisme. L'électromagnétisme peut être appelé « électrodynamisme » parce que c'est une interaction dynamique entre les forces électriques et magnétiques. L'électromagnétisme commence avec la charge électrique.

Les charges électriques sont la source créatrice des champs électriques. Un champ électrique est un champ qui exerce une force sur toute particule portant des charges électriques, en tout point de l'espace. Cela inclut l'électron, le proton et même les quarks, entre autres. Lorsqu'une force est exercée, les charges électriques se déplacent, un courant se forme et un champ magnétique est produit. Le champ magnétique modifié produit à son tour un courant électrique (en général en déplaçant des électrons). La description physique de l'interaction des particules chargées, des courants électriques, des champs électriques et des champs magnétiques est appelée « électromagnétisme ».

En 1928, Paul Dirac a écrit une théorie quantique relativiste de l'électromagnétisme. C'était l'ancêtre de l'électrodynamique quantique moderne, et elle a par conséquent les ingrédients essentiels de la théorie moderne. Cependant, le problème des infinis insolubles apparut dans sa théorie quantique relativiste. Des années plus tard, la renormalisation résoudra largement ce problème. Au début observée avec circonspection, comme une procédure provisoire par ses créateurs, la renormalisation a finalement été adoptée comme un outil important et cohérent pour l'électrodynamique quantique et d'autres branches de la physique. Aussi, à la fin des années 1940, les diagrammes de Feynman ont permis de décrire toutes les interactions possibles concernant un événement donné. Ces diagrammes ont montré que la force électromagnétique est due aux interactions de photons avec les autres particules.

Un exemple de prédiction de l'électrodynamisme quantique qui a été vérifiée expérimentalement est le décalage de Lamb. Elle fait référence à un effet par lequel la nature quantique du champ magnétique pousse les niveaux d'énergie d'un atome ou d'un ion à dévier légèrement de ce qu'ils seraient sans lui. Sa conséquence est de décaler ou de dédoubler les raies spectrales.

De la même manière, dans une onde électromagnétique se propageant librement, le courant peut aussi être juste un courant de déplacement virtuel, plutôt que faisant intervenir des vecteurs de charge. En théorie quantique des champs, sa description complète fait appel essentiellement à des particules virtuelles ayant une très courte durée de vie.

Dans les années 1960, les physiciens se sont aperçus que l'électrodynamique quantique ne marchait plus dans le cas des très hautes énergies. À partir de ces incohérences est né le modèle standard de la physique des particules, afin de remédier en théorie à ce problème. Il y a une autre extension de la théorie quantique des champs qui unifie les forces électromagnétique et nucléaire faible dans une nouvelle théorie : l'interaction électrofaible.

Le modèle standard contient de plus, aux hautes énergies, une unification de l'interaction électrofaible avec l'interaction forte, décrite par la chromodynamique quantique. Il postule aussi une connexion entre la gravité et une nouvelle théorie de jauge, mais en 2015 cette connexion reste méconnue. La prédiction par cette théorie du boson de Higgs pour expliquer la masse inertielle a été récemment confirmée expérimentalement par le Grand collisionneur de hadrons, ce qui fait aujourd'hui du modèle standard la meilleure description de la physique des particules (plus ou moins complète).

Les applications de la mécanique quantique incluent les semi-conducteurs, le transistor, le laser, le microscope électronique et la résonance magnétique nucléaire. Une catégorie spéciale d'applications est dédiée aux phénomènes quantiques macroscopiques tels que la superfluidité de l'hélium ou la supraconductivité. L'étude des semi-conducteurs a mené à l'invention de la diode, du transistor et du circuit intégré, éléments indispensables de l'électronique moderne.

Même dans un simple interrupteur pour une lampe, l'effet tunnel d'un objet quantique est vital, sinon les électrons du courant électrique ne peuvent pas traverser la barrière de potentiel créée par une couche d'oxyde. Les puces de mémoire flash, que l'on trouve dans les clés USB, utilisent aussi l'effet tunnel pour effacer leurs cellules mémoire.