Fonction de Pearson
Les fonctions de Pearson ont été créées pour représenter des distributions unimodales. Il en existe douze. Elles ont été inventées par Karl Pearson à la fin du XIXe siècle et au début du XXe siècle.
Historique
Le système de Pearson a été originellement conçu afin de modéliser des observations visiblement asymétriques. Les méthodes pour ajuster un modèle théorique aux deux premiers cumulants ou moments de données observées : toute distribution peut être étendue directement une famille de distributions adaptée. Sauf dans des cas pathologiques, une famille peut être adaptée à l'espérance (premier cumulant) et la variance (deuxième cumulant) de façon arbitraire, mais il était jusque là impossible de construire des densités de probabilité en prenant également en compte l'asymétrie (troisième cumulant standardisé) et la kurtosis (quatrième cumulant standardisé). Ce besoin est apparu quand il a fallu trouver des modèles adaptés à des observations visiblement asymétriques. Les exemples de Pearson citent des données de survie, usuellement asymétriques.
Dans son article original, Pearson (1895, p. 360) identifie quatre four types de distributions (numéroté de I à IV) en plus de la distribution normale (qu'il numérote originellement type V). La classification dépend du support des distributions, selon qu'il soit sur un intervalle borné, une demi-droite ou la droite réelle ; mais aussi selon leur asymétrie possible ou leur symétrie. Un deuxième papier (Pearson 1901) rectifie deux oublis : il redéfinit le type V (étant redéfinie de la loi normale, désormais la loi inverse-gamma) et introduit la fonction de type VI. Les deux papiers couvrent les cinq types principaux du système de Pearson (I, III, IV, V et VI). Un troisième papier de Pearson 1916 introduit de nouveaux types et sous-types (numérotés de VII à XII).
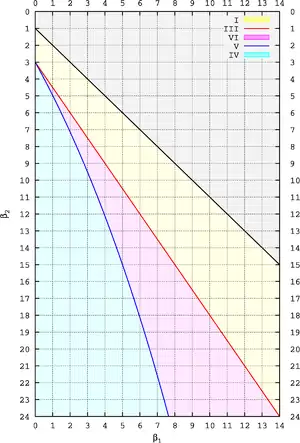
Rhind 1909 décrit un moyen simple de visualiser le paramètre spatial du système de Pearson, adopté par Pearson lui-même par la suite (Pearson 1916). Les types de Pearson sont caractérisés par deux quantités, couramment notées β1 et β2. La première correspond au carré de l'asymétrie : β1 = γ2
1 où γ1 est l'asymétrie, ou troisième moment standardisé. La deuxième est la kurtosis usuelle, ou quatrième moment standardisé : β2 = 3 + γ2. Les définitions modernes définissent la kurtosis γ2 à partir des cumulants plutôt que des moments, de sorte que pour la loi normale, on ait γ2 = 0 et β2 = 3, mais on garde ici la définition historique de β2 par Pearson.)
Beaucoup de lois asymétriques et/ou non-mésokurtiques connues de nos jours ne l'étaient pas dans les années 1890. Par exemple, la loi bêta était utilisée par Thomas Bayes comme loi a posteriori du paramètre d'une loi de Bernoulli dans ses travaux de 1763 sur les lois inverses. La loi beta a gagné en importance grâce au système de Pearson et est resté jusque dans les années 1940 conne la loi de Pearson de type I[1] (le type II de Pearson est un cas spécial du type I, mais n'est plus de nos jours considéré séparément du type I). De même, la loi gamma vient originellement de Pearson 1893 et Pearson 1895 et est resté jusque dans les années 1940 conne la loi de Pearson de type III[2]. La loi de type IV apparait dans Pearson 1895, et décrit comme cas spécial, ce qu'on appelle désormais la loi de Student, précédant les travaux de William Gosset de plusieurs années. Son article de 1901 présente les lois inverse-gamma (type V) et bêta prime (type VI).
Définition
Une densité p est définie comme toute solution de l'équation différentielle (Pearson et 1895 p.381) avec :
Selon Ord[3], Pearson a trouvé cette forme en partant d'abord de la forme de la dérivée logarithmique de la densité de la loi normale (qui est linéaire) puis en utilisant une relation de récurrence pour les valeurs de la fonction de densité de la loi hypergéométrique (qui donne la forme d'une fraction rationnelle, linéaire au numérateur et quadratique au dénominateur).
Le paramètre a détermine un point stationnaire, et donc, sous certaines conditions, un mode de la distribution, car on peut déduire de l'équation différentielle que
L'équation différentielle est du premier ordre à coefficients variables et peut donc être résolue :
L'intégrale dans la solution peut se simplifier grandement pour certains cas de l'intégrande. Pearson distingue deux cas, déterminé par le signe du discriminant de l'équation différentielle, et donc le nombre de racines réelles du polynôme f(x) = b2x2 + b1x + b0.
Fonctions de Pearson
Pearson IV
La fonction de Pearson IV correspond au cas où la fonction f définie auparavant a un discriminant strictement négatif. On peut alors la réécrire sous la forme :
Le paramètre α > 0 (bien défini en raison du signe du discriminant) est un paramètre d'échelle, on a deux paramètres de forme m = 1⁄b2 > 1/2 et , et le paramètre λ = b1⁄2b2 est un paramètre de localisation.
Après simplification, la densité de probabilité p, pour x réel, vaut : où k est un facteur de normalisation. Si m ≤ 1/2, la fonction n'est pas normalisable.
La fonction de Pearson IV est en fait une version asymétrique de la loi de Student ; de fait, on retrouve la loi de Student avec r = 2m–1 degrés de liberté pour ν = 0.
Pour m = 1, la distribution de Pearson IV est une forme asymétrique de la loi de Cauchy (ou distribution de Breit-Wigner).
La fonction a un mode (sommet) unique placé en elle présente deux points d'inflexion situés en .
Sa moyenne vaut pour m > 1. La moyenne est infinie si ν = 0 et m ≤ 1.
Sa variance vaut pour m > 3/2. La variance est infinie si m ≤ 3/2.
Le facteur de normalisation vaut : où Γ est la fonction Gamma d'Euler.
Pearson VII
La fonction de Pearson IV correspond au cas particulier de la fonction IV où le paramètre de forme ν, qui détermine l'asymétrie, est supposé nul. La distribution devient alors symétrique.
La VIIe fonction de Pearson est définie alors, pour x entier, par Le facteur de normalisation vaut alors : où B est la fonction bêta.
On écrit parfois une expression simplifiée en posant σ = α/√2m–3 :
Le paramètre m détermine alors la kurtosis de la distribution ;
- m < 1 : distribution dite super-lorentzienne ;
- m = 1 : distribution de Cauchy/Lorentz (lorentzienne)/Breit-Wigner ;
- m → ∞ : distribution de Gauss-Laplace (gaussienne, loi normale).
Elle est utilisée en radiocristallographie pour modéliser le profil des pics de diffraction (voir aussi Fonction de Voigt).
Autre paramétrisation : la loi de Student
La fonction de Pearson VII permet aussi de retrouver la fonction de densite de la loi de Student en fixant le jeu de paramètres :
La contrainte m > 1/2 est ainsi toujours vérifiée.
On obtient alors la densité :
Autres cas
En considérant le cas où f a un discriminant positif (b2
1 – 4 b2 b0 ≥ 0), on a alors deux racines réelles a1 et a2 (pas forcément distinguées) :
La forme générale de la densité peut alors se réécrire :
Pearson le désigne comme le "cas logarithmique" (logarithmic case), car l'intégrale se résout alors en utilisant uniquement la fonction logarithme :
En posant , il vient :
Pearson I
Les fonctions de Pearson de type I (une généralisation de la loi bêta) correspondent au cas où les deux racines sont de signes opposés (a1 < 0 < a2). La densité p n'est alors définie que sur l'intervalle (a1 , a2). En se ramenant à l'intervalle (0 ; 1) par la substitution x = a1 + y (a2 – a1), et en posant :
l'écriture de la densité se simplifie en :
Ainsi, suit une loi bêta B(m1 + 1 , m2 + 1) avec . La condition m1, m2 > −1 est nécessaire et suffisante pour que p définisse une densité de probabilités.
Pearson II
Les fonctions de Pearson de type II sont un cas particulier des fonctions de type I, où les paramètres rendent la densité symétrique.
Pour la courbe de la fonction de Pearson II[4]
avec
L'ordonnée y est la fréquence de ∑ d2. Elles sont utilisées dans le calcul des tables de coefficients de corrélation dans la corrélation de Spearman pour un échantillon de moins de 100. Après, la distribution se rapproche d'une loi de Student.
Pearson III
En posant il vient que les fonctions de Pearson de type III regroupent les lois gamma et les lois du χ2.
Pearson V
En posant on voit que les fonctions de Pearson de type V correspondant aux lois inverse-gamma.
Pearson VI
En posant il vient que les fonctions de Pearson de type VI regroupent les lois bêta prime et les lois de Fisher.
Pearson VIII
La forme générale de la densité peut s'écrire[5]:
Pearson IX
La forme générale de la densité peut s'écrire[5]:
Pearson X
La forme générale de la densité peut s'écrire[5]: On reconnait alors la loi exponentielle.
Pearson XI
La forme générale de la densité peut s'écrire[5]: C'est donc un cas particulier de la loi de Pareto.
Pearson XII
La forme générale de la densité peut s'écrire[5]: C'est donc un cas particulier du type I.
Généralisations
Le système de Pearson est défini à partir d'une équation différentielle. En considérant d'autres fonctions, on peut construire d'autres systèmes, comme celui de Burr ou de Johnson[5] - [6]
Système de Burr
Le système de Burr regroupe les distributions telles que leur fonctions de répartition F vérifient l'équation différentielle[7]: où g est une fonction positive.
Burr a déterminé douze types de solutions, selon le choix de g[8] - [9] - [10]; celle qu'on appelle usuellement loi de Burr correspond au 12e et dernier cas.
Système de Johnson
Le système de Johnson repose sur une transformation de données normalement distribuées, caractérisée par une fonction et quatre paramètres dits de translation. En considérant φ la fonction de densité de la loi normale centrée réduite, il pose une fonction h supposément croissante et dérivable, et quatre paramètres, δ, λ > 0, γ, ξ réels, il transforme la variable en ce qui permet d'obtenir un modèle de fonction de densité : Johnson s'attarde sur trois types de fonctions[11]:
- une fonction à support borné :
- une fonction à support sur la demi-droite réelle :
- une fonction à support non borné (en) :
Voir aussi
Bibliographie
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pearson distribution » (voir la liste des auteurs).
- (en) Karl Pearson, « Contributions to the Mathematical Theory of Evolution. II. Skew Variation in Homogeneous Material : A (1887-1895) », Philosophical Transactions of the Royal Society of London, vol. 186, , p. 343–414 (DOI 10.1098/rsta.1895.0010, JSTOR 90649)
- (en) Karl Pearson, « Mathematical Contributions to the Theory of Evolution. X. Supplement to a Memoir on Skew Variation : Series A, Containing Papers of a Math. or Phys. Character (1896-1934) », Philosophical Transactions of the Royal Society of London, vol. 197, , p. 443–459 (DOI 10.1098/rsta.1901.0023, JSTOR 90841)
- (en) Karl Pearson, « Mathematical Contributions to the Theory of Evolution. XIX. Second Supplement to a Memoir on Skew Variation : Series A, Containing Papers of a Math. or Phys. Character (1896-1934) », Philosophical Transactions of the Royal Society of London, vol. 216, , p. 429–457 (DOI 10.1098/rsta.1916.0009, JSTOR 91092)
- (en) A. Rhind, « Tables to facilitate the computation of the probable errors of the chief constants of skew frequency distributions », Biometrika, vol. 7, nos 1/2, juillet–octobre 1909, p. 127–147 (DOI 10.1093/biomet/7.1-2.127, JSTOR 2345367, lire en ligne)
- (en) J.K. Ord, Families of Frequency Distributions, London, Griffin.
Liens externes
- (en) A Guide to the Pearson Type IV Distribution, Joel Heinrich, University of Pennsylvania, 2004
- (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne)
- (en) Eric W. Weisstein, « Pearson Type III Distribution », sur MathWorld.
Notes et références
- (en) Jeff Miller et al., « Beta distribution », sur Earliest Known Uses of Some of the Words of Mathematics, (consulté le ).
- (en) Jeff Miller et al., « Gamma distribution », sur Earliest Known Uses of Some of the Words of Mathematics, (consulté le ).
- Ord 1972, p. 2.
- (en) Philip H. Ramsey, « Critical Values for Spearman's Rank Order Correlation », Journal of Educational Statistics, vol. 14, no 3, , p. 245–253 (JSTOR 1165017).
- (en) Bachioua Lahcene, « On Pearson families of distributions and its applications », African Journal of Mathematics and Computer Science Research, vol. 6, no 5, , p. 108-117 (ISSN 2006-9731, DOI 10.5897/AJMCSR2013.0465).
- (en) D. C. M. Leslie, « Determination of Parameters in the Johnson System of Probability Distributions », Biometrika, vol. 46, nos 1/2, , pp. 229-231 (DOI 10.2307/2332826).
- (en) Tanujit Chakraborty, Suchismita Das et Swarup Chattopadhyay, « A New Method for Generalizing Burr and Related Distributions », Mathematica Slovaca, vol. 72, no 1, (DOI 10.1515/ms-2022-0016).
- (en) R.N. Rodriguez, Encyclopedia of Statistical Science, vol. 1, New York, John Wiley & Sons, , « Burr distributions ».
- (en) M. Z. Raqab, « Order Statistics From the Burr Type X Model », Computers Math. Applic., vol. 36, no 4, , pp. 111-120 (lire en ligne).
- (en) T.R.L. Fry, Univariate and Multivariate Burr Distributions: A Survey, (DOI 10.22004/ag.econ.266976, lire en ligne).
- (en) N.L. Johnson, « Systems of Frequency Curves Generated by Methods of Translation », Biometrika, Oxford University Press, vol. 36, nos 1/2, , p. 149-176.




![{\displaystyle f(x)=b_{2}\left[\left(x+{\frac {b_{1}}{2b_{2}}}\right)^{2}+\left({\frac {\sqrt {4b_{2}b_{1}-b_{0}^{2}}}{2b_{2}}}\right)^{2}\right]=b_{2}\left[(x-\lambda )^{2}+\alpha ^{2}\right]}](https://img.franco.wiki/i/1987b230bb683a1b9f0fbcd2bb6d12397beeaace.svg)

![{\displaystyle p(x)=k\cdot \left[1+\left({\frac {x-\lambda }{\alpha }}\right)^{2}\right]^{-m}\cdot \exp \left[-\nu \cdot \arctan \left({\frac {x-\lambda }{\alpha }}\right)\right]}](https://img.franco.wiki/i/be535ab9897e154180f70a98032931fc78be31a2.svg)





![{\displaystyle p(x)=k\left[1+{\frac {(x-\lambda )^{2}}{\alpha ^{2}}}\right]^{-m}.}](https://img.franco.wiki/i/b9f2ba074f3354902baf7e765606f8d022d9ecc9.svg)

![{\displaystyle p(x)={\frac {1}{\sigma {\sqrt {2m-3}}\,\mathrm {B} (m-{\frac {1}{2}},{\frac {1}{2}})}}\left[1+{\frac {(x-\lambda )^{2}}{\sigma ^{2}(2m-3)}}\right]^{-m}}](https://img.franco.wiki/i/a27c48d7b7681ff6689e29f7639e2e2e8798067b.svg)


![{\displaystyle {\begin{aligned}a_{1}&={\frac {-b_{1}-{\sqrt {b_{1}^{2}-4b_{2}b_{0}}}}{2b_{2}}},\\[5pt]a_{2}&={\frac {-b_{1}+{\sqrt {b_{1}^{2}-4b_{2}b_{0}}}}{2b_{2}}}.\end{aligned}}}](https://img.franco.wiki/i/c1a5a1565a6894940b412c87e8058a915d53a6f7.svg)




![{\displaystyle {\begin{aligned}m_{1}&={\frac {a-a_{1}}{b_{2}(a_{1}-a_{2})}},\\[5pt]m_{2}&={\frac {a-a_{2}}{b_{2}(a_{2}-a_{1})}},\end{aligned}}}](https://img.franco.wiki/i/fada7302ebe6668b8a1614ed6bd3e87f324e34e3.svg)



















