Variance (mathématiques)

En statistique et en théorie des probabilités, la variance est une mesure de la dispersion des valeurs d'un échantillon ou d'une variable aléatoire. Elle exprime la moyenne des carrés des écarts à la moyenne, aussi égale à la différence entre la moyenne des carrés des valeurs de la variable et le carré de la moyenne, selon le théorème de König-Huygens. Ainsi, plus l'écart à la moyenne est grand plus il est prépondérant dans le calcul total (voir la fonction carré) de la variance qui donnerait donc une bonne idée sur la dispersion des valeurs.

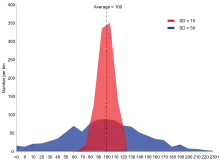
Exemple d'échantillons pour deux populations ayant la même moyenne mais des variances différentes. La population en rouge a une moyenne de 100 et une variance de 100 (écart-type = SD = standard deviation = 10). La population en bleu a une moyenne de 100 et une variance de 2 500 (écart-type = SD = 50).

La variance est toujours positive, et ne s’annule que s’il n’y a essentiellement qu’une seule valeur. Sa racine carrée définit l’écart type σ, d’où la notation $\sigma ^{2}=V=\mathbb {V} (X)=\mathrm {Var(X)}$ .

La variance est quadratique et invariante par translation. Elle peut être estimée à l’aide d’un échantillon et de la moyenne empirique ou de l’espérance si celle-ci est connue.

La variance apparait comme un cas particulier de covariance. Elle se généralise aussi pour des vecteurs aléatoires.

Pour une série statistique

Formules

Étant donné une série statistique d’une variable réelle $(x 1, x 2, ..., x n)$ , dont on a calculé la moyenne ${\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$ , la variance est la moyenne des carrés des écarts à cette moyenne :

V={\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}

Un développement du carré mène à la reformulation suivante[1] :

V=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{2}\right)-{\overline {x}}^{2}

autrement dit la variance est la différence entre la moyenne des carrés et le carré de la moyenne.

Quand la série prend les valeurs $x 1, x 2, ..., x n$ avec les fréquences $f 1, f 2, ..., f n$ , sa variance est :

V=\sum _{i=1}^{n}f_{i}\left(x_{i}-{\overline {x}}\right)^{2}=\left(\sum _{i=1}^{n}f_{i}x_{i}^{2}\right)-{\overline {x}}^{2}.

La variance est un indicateur de dispersion des valeurs, c’est-à-dire qu’elle est toujours positive, ne s’annule que pour une série statistique dont tous les termes ont la même valeur, elle est d’autant plus grande que les valeurs sont étalées, et invariante par ajout d’une constante. Son calcul peut sembler plus compliqué que celui d’autres indicateurs de dispersion, comme l’écart interquartile ou l’écart absolu moyen, mais contrairement à ces derniers, elle est cumulative : si on rassemble $k$ séries statistiques en une seule, la variance globale peut être calculée à partir de l’effectif $n i$ , la variance $V i$ et la moyenne ${\overline {x}}_{i}$ de chaque série initiale par la formule

V={\frac {1}{N}}\sum _{i=1}^{k}n_{i}(V_{i}+({\overline {x}}-{\overline {x}}_{i})^{2})

où $N=\sum _{i=1}^{k}n_{i}$ est l’effectif total et ${\overline {x}}={\frac {1}{N}}\sum _{i=1}^{k}n_{i}{\overline {x}}_{i}$ , est la moyenne globale. Autrement dit, la variance globale est la somme de la variance des moyennes et de la moyenne des variances, même si cette deuxième composante est souvent négligée.

Transformation affine

Si on applique une fonction affine $f:x\mapsto ax+b$ aux termes d’une série statistique $(x 1, x 2, ..., x n)$ , la variance est multipliée par $a 2$ . Autrement dit, la variance est homogène de degré 2 et invariante par translation.

Calcul itératif

Le calcul effectif de la variance pour une série statistique ne repose pas sur la traduction directe des formules ci-dessus, sauf pour le calcul à la main sur de petites séries. On utilise plutôt un algorithme itératif qui améliore la précision[alpha 1] :

c = 0
s = x₁
pour j de 2 à n
  s = s+x_j
  c = c+(j x_j − s)²/(j(j−1))
renvoyer c/n

Pour une variable aléatoire réelle

Expression

Étant donné une variable aléatoire réelle $X$ admettant une espérance $\mathbb {E} (X)$ , la variance[alpha 2] est le moment centré d’ordre 2 : $\mathbb {V} (X)=\mathbb {E} \left[(X-\mathbb {E} (X))^{2}\right]$ . La formule de Koenig-Huygens donne l’expression équivalente $\mathbb {V} (X)=\mathbb {E} (X^{2})-(\mathbb {E} (X))^{2}$ .

Ces deux formules n’ont de sens que si $\mathbb {E} (X^{2})$ existe[2], autrement dit si la variable admet un moment d’ordre 2. Cela est toujours le cas pour une variable aléatoire bornée, et en particulier pour une variable aléatoire qui n’a qu’un nombre fini de valeurs possibles. Mais pour une variable aléatoire non bornée, l’existence de l’espérance et du moment d’ordre 2 dépendent de la convergence d’une série ou d’une intégrale. Ainsi, une loi de Pareto n’admet une espérance que si son paramètre $k$ est strictement supérieur à 1, et n’admet une variance que si $k > 2$ .

Pour une variable aléatoire n’admettant qu’un nombre fini de valeurs notées $(x 1, ... , x k)$ , et en notant $(p 1, ... , p k)$ les probabilités associées, on retrouve l’expression de la variance

\mathbb {V} (X)=\sum _{i=1}^{k}p_{i}(x_{i}-{\overline {x}})^{2}=\left(\sum _{i=1}^{k}p_{i}x_{i}^{2}\right)-{\overline {x}}^{2}=\left(\sum _{i=1}^{k}p_{i}x_{i}^{2}\right)-\left(\sum _{i=1}^{k}p_{i}x_{i}\right)^{2}

Pour une variable aléatoire discrète avec un nombre infini de valeurs, on reprend la même formule en remplaçant la somme par une série[3].

Dans le cas d’une variable aléatoire à densité, la variance est définie par :

\mathbb {V} (X)=\sigma ^{2}=\int (x-\mu )^{2}\,f(x)\,dx\,

où $f$ est la densité de probabilité et $μ$ est l'espérance mathématique de la variable aléatoire $X$

\mu =\int x\,f(x)\,\mathrm {d} x\,

La variance d'une variable aléatoire continue $X$ peut aussi se calculer de la façon suivante :

\mathbb {V} (X)=\int x^{2}\,f(x)\,\mathrm {d} x\,-\mu ^{2}

Transformation affine

Comme pour une série statistique, l’effet d’une transformation affine sur une variable aléatoire affecte celle-ci par la formule[4] - [alpha 3] : $\mathbb {V} (aX+b)=a^{2}\mathbb {V} (X)$ .

Combinaison linéaire

Si deux variables aléatoires $X$ et $Y$ admettent une variance, alors leur somme aussi et elle s’écrit[alpha 4] $\mathbb {V} (X+Y)=\mathbb {V} (X)+\mathbb {V} (Y)+2\mathrm {Cov} (X,Y)$ , où $\mathrm {Cov} (X,Y)$ est la covariance. La relation s’étend à toute combinaison linéaire de variables admettant une variance[alpha 5] :

\mathbb {V} \left(\sum _{i=1}^{n}{a_{i}\,X_{i}}\right)=\sum _{i=1}^{n}a_{i}^{2}\,\mathbb {V} (X_{i})+2\sum _{1\leq i<j\leq n}\,a_{i}a_{j}\,\operatorname {Cov} (X_{i},X_{j})=\sum _{i=1}^{n}\sum _{j=1}^{n}a_{i}a_{j}\operatorname {Cov} (X_{i},X_{j})

\mathbb {V} \left(\sum _{i=1}^{n}{X_{i}}\right)=\sum _{i=1}^{n}\mathbb {V} (X_{i})+2\sum _{1\leq i<j\leq n}\operatorname {Cov} (X_{i},X_{j})

Somme de variables indépendantes

Si $X$ et $Y$ sont deux variables indépendantes, leur covariance est nulle donc on trouve $\mathbb {V} (X+Y)=\mathbb {V} (X)+\mathbb {V} (Y)$ mais la réciproque est fausse[alpha 4]. Cette relation ne doit pas être confondue avec la linéarité satisfaite par l’espérance. En particulier $\mathbb {V} (X-Y)=\mathbb {V} (X)+\mathbb {V} (Y)$ et plus généralement $\mathbb {V} (aX+bY)=a^{2}\mathbb {V} (X)+b^{2}\mathbb {V} (Y)$ .

Plus généralement, la variance d’une somme de variables indépendantes est égale à la somme des variances. Ce résultat implique que pour un échantillon de $n$ variables de même variance $σ 2$ , la variance de la moyenne empirique s’écrit[5] - [alpha 6] $\mathbb {V} ({\overline {X}})={\frac {\sigma ^{2}}{n}}$ .

Produit de variables indépendantes

La variance d'un produit de deux variables aléatoires indépendantes $X$ et $Y$ de variances finies est exprimée en fonction de celles des deux variables par la formule suivante[alpha 4] - [note 1]

{\begin{aligned}\mathbb {V} (XY)&=\mathbb {V} (X)\mathbb {V} (Y)+\mathbb {V} (X)(\mathbb {E} (Y))^{2}+\mathbb {V} (Y)(\mathbb {E} (X))^{2}\\&=\mathbb {V} (X)\mathbb {E} (Y^{2})+\mathbb {V} (Y)(\mathbb {E} (X))^{2}\\&=\mathbb {V} (Y)\mathbb {E} (X^{2})+\mathbb {V} (X)(\mathbb {E} (Y))^{2}\end{aligned}}

Estimation

Estimateur ponctuel

À partir d’un échantillon de variables aléatoires réelles $(X 1, ... , X n)$ indépendantes et relevant d’une même loi de probabilité, la variance $σ 2$ de cette loi peut être estimée à l’aide de la variance empirique[alpha 7]

S^{2}={\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}

où ${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$ est la moyenne empirique.

Cet estimateur est cependant biaisé, car $\mathbb {E} (S^{2})={\frac {n-1}{n}}\sigma ^{2}$ .

Démonstration

On note $μ$ l’espérance commune aux variables de l’échantillon.

On développe $nS^{2}=\sum _{i=1}^{n}X_{i}^{2}-2{\overline {X}}\sum _{i=1}^{n}X_{i}+n{\overline {X}}^{2}=\sum _{i=1}^{n}X_{i}^{2}-n{\overline {X}}^{2}$ .

Or on trouve ${\overline {X}}^{2}={\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}X_{i}X_{j}$ avec pour tout $i$ , $\mathbb {E} (X_{i}^{2})=\mathbb {V} (X_{i})+(\mathbb {E} (X_{i}))^{2}=\sigma ^{2}+\mu ^{2}$ d’après la formule de Koenig-Huygens, et pour tout $i\neq j$ , $\mathbb {E} (X_{i}X_{j})=\mathbb {E} (X_{i})\mathbb {E} (X_{j})=\mu ^{2}$ par indépendance.

On en déduit $\mathbb {E} ({\overline {X}}^{2})={\frac {1}{n^{2}}}(n(\sigma ^{2}+\mu ^{2})+n(n-1)\mu ^{2})={\frac {1}{n}}(\sigma ^{2}+n\mu ^{2})$ d’où l’on tire $\mathbb {E} (nS^{2})=n(\sigma ^{2}+\mu ^{2})-(\sigma ^{2}+n\mu ^{2})=(n-1)\sigma ^{2}$ donc $\mathbb {E} (S^{2})={\frac {n-1}{n}}\sigma ^{2}$ .

Si $n > 1$ , on définit alors un estimateur non biaisé ${\widetilde {S}}^{2}={\frac {n}{n-1}}S^{2}$ par linéarité de l’espérance.

Pour estimer la variance d'une population entière à partir de celle mesurée sur un échantillon de taille $n$ , la variance estimée est obtenue en multipliant la variance mesurée sur l'échantillon par $n / n - 1$ . Dans le cas (plus rare en pratique) d'un tirage sans remise dans une population de taille $N$ , il faut utiliser l'estimateur[6] ${\frac {N-1}{N}}{\widetilde {S}}^{2}$ . Dans le cas où l’espérance $μ$ des variables de l’échantillon est connue, l’estimateur direct $T={\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}$ est déjà sans biais.

Démonstration

Comme dans la démonstration du biais de $S 2$ , on trouve :

$nT=\sum _{i=1}^{n}X_{i}^{2}-2\mu \sum _{i=1}^{n}X_{i}+\mu ^{2}$ .

Donc $\mathbb {E} (nT)=n(\sigma ^{2}+\mu ^{2})-2n\mu \mathbb {E} ({\overline {X}})+n\mu ^{2}=n(\sigma ^{2}+\mu ^{2})-2n\mu ^{2}+n\mu ^{2}=n\sigma ^{2}$ et $\mathbb {E} (T)=\sigma ^{2}$ .

Ces trois estimateurs sont convergents.

Démonstration

D’après la loi des grands nombres, la moyenne empirique converge presque sûrement vers l’espérance $μ$ et la moyenne empirique des carrés ${\frac {1}{n}}\sum _{i=1}^{n}X_{i}^{2}$ converge presque sûrement vers $σ 2 + μ 2$ , ce qui montre que les trois estimateurs de la variance convergent vers $σ 2$ lorsque $n \to +\infty$ .

Intervalle de confiance

L’obtention d’un intervalle de confiance pour la variance d’une loi de probabilité à partir d’un échantillon dépend du type de loi.

Pour une famille de lois dépendant d’un seul paramètre, comme les lois de Bernoulli, les lois géométriques, exponentielles ou les lois de Poisson, il suffit d’utiliser un intervalle de confiance sur le paramètre. Pour une famille de lois dépendant d’au moins deux paramètres, on utilise un estimateur convergent ayant un seul paramètre directement relié à la variance de la loi initiale. Ainsi, pour un échantillon de $n$ variables gaussiennes $(X 1, ... , X n)$ dont l’espérance est inconnue, le quotient de la variance empirique sans biais multiplié par $(n -1)$ par la variance réelle suit une loi de khi-deux avec $n - 1$ degrés de liberté d’après le théorème de Cochran.

Éléments d'histoire

Ronald Fisher employa, le premier, le mot de variance, dans un article de 1918 intitulé « The Correlation between Relatives on the Supposition of Mendelian Inheritance » [@ 1] où il définit la variance comme le carré de l'écart type. Dans ce document il préfère clairement la variance à l'écart type en tant que mesure de la variabilité d'un phénomène observé. Il utilise ce terme à nouveau au congrès de mathématiques de Toronto en 1924[@ 2]. C'est lui qui définit aussi l'analyse de la variance telle qu'on la pratique aujourd'hui dans son livre « Statistical methods for research workers » paru en 1925[@ 3] - [alpha 7].

Applications

Le calcul de la variance permet d’en déduire l’écart type[alpha 8] $\sigma (X)={\sqrt {\mathbb {V} (X)}}$ , qui est homogène à la variable aléatoire, au sens mathématique du terme comme en analyse dimensionnelle.

La variance d’une série statistique apparait dans le calcul des coefficients de la régression linéaire.

L’analyse de la variance (ANOVA) rassemble des méthodes d’études de comparaisons entre échantillons sur une ou plusieurs variables quantitatives.

La variance d’une variable aléatoire intervient dans le théorème central limite ainsi que dans l’inégalité de Bienaymé-Tchebychev.

Variance conditionnelle

Soient deux variables aléatoires $Y$ et $X$ . On appelle variance conditionnelle de $Y$ sachant $X$ la variable aléatoire correspondant à l'espérance conditionnelle sachant X du carré de l'écart de Y à l'espérance conditionnelle :

\operatorname {Var} (Y|X)=\mathbb {E} \left([Y-\mathbb {E} (Y|X)]^{2}|X\right).

Comme toute variable conditionnelle, elle est fonction de $X$ .

La variance de $Y$ est liée à la variance et l'espérance conditionnelles par le théorème de la variance totale :

\operatorname {Var} (Y)=\mathbb {E} (\operatorname {Var} [Y|X])+\operatorname {Var} (\mathbb {E} [Y|X]).

Variance d'un vecteur aléatoire

Si l'on définit $X k \times 1$ comme un vecteur aléatoire qui comporte $k$ variables et $Μ$ comme le vecteur des $k$ espérances de $X$ , on définit alors la variance comme :

Définition — $\Sigma _{k\times k}\equiv \operatorname {Var} [X_{k\times 1}]\equiv \mathbb {E} \left[(X_{k\times 1}-\mathrm {M} )\ ^{\operatorname {t} }(X_{k\times 1}-\mathrm {M} )\right]$

Il s'agit alors d'une matrice carrée de taille $k$ , appelée matrice de variance-covariance, qui comporte sur sa diagonale les variances de chaque composante du vecteur aléatoire et en dehors de la diagonale les covariances. Cette matrice est symétrique et semi-définie positive ; elle est définie positive si et seulement si la seule combinaison linéaire certaine (c'est-à-dire presque sûrement constante) des composantes du vecteur aléatoire est celle dont tous les coefficients sont nuls. Le cas contraire signifie que les réalisations du vecteur $X$ sont presque sûrement confinées à un hyperplan.

On a les propriétés suivantes :

Propriété — Si $V$ est une matrice carrée de taille $k,\operatorname {Var} [V_{k\times k}X_{k\times 1}]=V\operatorname {Var} [X]\ ^{\operatorname {t} }V$

Notes et références

Notes

Les deux autres formes sont déduites de la première par factorisation des variances, puis substitution de l'égalité du théorème de Koenig-Huygens $\mathbb {V} (X)=\mathbb {E} (X^{2})-(\mathbb {E} (X))^{2}\iff \mathbb {V} (X)+(\mathbb {E} (X))^{2}=\mathbb {E} (X^{2})$ .

« D'autres formules de la variance » (consulté le 13 avril 2022)
L’existence d’un moment d’ordre 2 implique notamment l’existence de l’espérance.
Une variable aléatoire discrète ne peut admettre qu’un ensemble dénombrable de valeurs avec une probabilité non nulle.
Pour cette démonstration, il est utile de rappeler une des propriétés de l'espérance : $\mathbb {E} (aX+b)=a\operatorname {E} (X)+b$ . On a alors $\operatorname {Var} (aX+b)=\mathbb {E} [(aX+b-\mathbb {E} [aX+b])^{2}]=\mathbb {E} [(aX+b-a\mathbb {E} [X]-b)^{2}]=\mathbb {E} [(aX-a\mathbb {E} [X])^{2}]=\mathbb {E} [a^{2}(X-\mathbb {E} [X])^{2}]=a^{2}\mathbb {E} [(X-\mathbb {E} [X])^{2}]=a^{2}\operatorname {Var} (X)$
$\operatorname {Var} ({\overline {X}})=\operatorname {Var} \left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)={\frac {1}{n^{2}}}\operatorname {Var} \left(\sum _{i=1}^{n}X_{i}\right)={\frac {1}{n^{2}}}n\operatorname {Var} (X)={\frac {\operatorname {Var} (X)}{n}}$
Rémy Clairin, Philippe Brion, Manuel de sondages, Applications aux pays en développement, Documents et manuels du CEDEP, février 97, (ISBN 2-87762-082-4), page 17 ).

Ouvrages spécialisés

Saporta 2011, §5.3.2.3 « La variance et l’écart-type »
- Saporta 2006, p. 25
Rioul 2008, p. 142
Saporta 2006, p. 26
Rioul 2008, p. 183-185
Dodge 2010, p. 508
Dodge 2010, p. 556
Dodge 2010, p. 506

Articles publiés sur internet

[PDF] (en) Ronald A. Fisher, « The Correlation between Relatives on the Supposition of Mendelian Inheritance. », Philosophical Transactions of the Royal Society of Edinburgh., vol. 52,‎ 1918, p. 399–433 (lire en ligne).
[PDF] Jean-Paul Benzécri, « Histoire et Préhistoire de l'Analyse des données : Partie 3 », Les Cahiers de l'analyse des données, vol. 1, n^o 3,‎ 1976, p. 221-241 (lire en ligne, consulté le 24 avril 2012).
[PDF] J.-M. Faverge, « III. - L'analyse de la variance en psychologie », L'Année psychologique, vol. 49, n^o 1,‎ 1948, p. 341-358 (lire en ligne).

Voir aussi

Bibliographie

(fr) Gilbert Saporta, Probabilités, Analyse des données et Statistiques, Paris, Éditions Technip, 2006, 622 p. [détail des éditions] (ISBN 978-2-7108-0814-5, présentation en ligne).
(fr) Olivier Rioul, Théorie des probabilités, Paris, Editions Hermes sciences, 2008, 364 p. (ISBN 978-2-7462-1720-1).
Yadolah Dodge, « The Concise Encyclopaedia of Statistics », New York, Springer, 2010, 622 p. (ISBN 978-0-387-31742-7, lire en ligne).

Liens externes

Eric W. Weisstein, « Variance », MathWorld--A Wolfram Web Resource (consulté le 25 avril 2012)
« Calcul en ligne de la variance », Calculis

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

Variance (mathématiques)

Pour une série statistique

Formules

Transformation affine

Calcul itératif

Pour une variable aléatoire réelle

Expression

Transformation affine

Combinaison linéaire

Somme de variables indépendantes

Produit de variables indépendantes

Estimation

Estimateur ponctuel

Intervalle de confiance

Éléments d'histoire

Applications

Variance conditionnelle

Variance d'un vecteur aléatoire

Notes et références

Notes

Ouvrages spécialisés

Articles publiés sur internet

Voir aussi

Bibliographie

Articles connexes

Liens externes