Fonction bornée
En mathématiques, une fonction est dite bornée si l'ensemble de ses valeurs est borné.
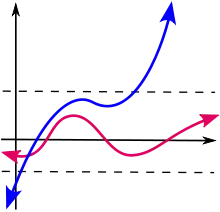
Schéma d'une fonction bornée (rouge) et d'une fonction non bornée (bleu). Intuitivement, le graphe d'une fonction bornée reste dans une bande horizontale, contrairement au graphe d'une fonction non bornée.
Pour une fonction f définie sur un ensemble X et à valeurs réelles ou complexes, cela revient à dire qu'il existe un nombre réel M tel que pour tout x dans X,
Une fonction à valeurs réelles est dite majorée (resp. minorée) si l'ensemble de ses valeurs possède un majorant (resp. minorant) réel. Elle est bornée si et seulement si elle est à la fois majorée et minorée.
Exemples
- La fonction sinus est bornée (minorée par –1 et majorée par 1).
- La fonction définie pour tous les réels x à l'exception de 0 est non bornée. À mesure que x s'approche 0, les valeurs de cette fonction deviennent de plus en plus grandes. Cette fonction peut être rendue bornée si on la restreint par exemple à [1, +∞[.
- La fonction définie pour tout réel x est bornée (l'ensemble de ses valeurs est l'intervalle ]0, 1]).
- La fonction circulaire réciproque arc tangente est bornée : pour tout réel x, .
- Une suite bornée est une fonction bornée définie sur l'ensemble ℕ des entiers naturels. L'ensemble de toutes les suites bornées forme l'espace des suites bornées, noté ℓ∞.
- Toute fonction continue de [0, 1] dans ℝ est bornée. Plus généralement :
- toute fonction continue d'un espace compact dans un espace métrique est bornée (cf. Théorème des valeurs extrêmes pour plus de détails) ;
- tout fonction localement bornée d'un espace dénombrablement compact dans ℝ est bornée et atteint ses bornes (voir Passage du local au global).
- La fonction de Dirichlet, qui prend la valeur 1 si x est un nombre rationnel et 0 si x est un nombre irrationnel, est non continue mais bornée. L'ensemble des fonctions réelles bornées définies sur [0, 1] est beaucoup plus grand que le sous-ensemble des fonctions continues sur cet intervalle.
Remarques
- L’ensemble des fonctions réelles bornées sur un même ensemble constitue un sous-espace vectoriel stable aussi par multiplication, ce qui en fait une algèbre normée par la norme infini. Plus généralement, cet ensemble est stable par composition par une fonction continue. Cela implique notamment que toute variable aléatoire réelle bornée admet des moments à n’importe quel ordre.
- Toute fonction monotone bornée sur un intervalle possède en chaque point une limite finie à gauche et une à droite : c'est le théorème de la limite monotone.
- Toute fonction entière bornée est constante : c'est le théorème de Liouville.
Notion connexe
Une famille de fonctions est uniformément bornée (en) si la réunion de leurs ensembles de valeurs est borné.
Article connexe
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.




