Fonction de Dirichlet

En mathématiques, la fonction de Dirichlet est la fonction indicatrice 1_ℚ de l'ensemble des rationnels ℚ, c'est-à-dire que 1_ℚ(x) = 1 si x est un nombre rationnel et 1_ℚ(x) = 0 si x n'est un pas un nombre rationnel (c'est-à-dire un nombre irrationnel).

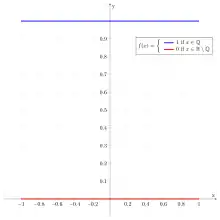
Représentation graphique de la fonction de Dirichlet, deux lignes parallèles qui semblent solides. La ligne bleue (resp. rouge) représente les nombres rationnels (resp. irrationnels), qui sont proches les uns des autres dans les réels. Le graphe contient un nombre indénombrable (resp. dénombrable) de trous dans la ligne bleue (resp. rouge), mais comme ils sont de longueur nulle on ne les voit pas.

Elle est nommée en l'honneur du mathématicien Peter Gustav Lejeune Dirichlet[1]. C'est un exemple de fonction pathologique qui fournit un contre-exemple à beaucoup de situations.

Propriétés topologiques

La fonction de Dirichlet est continue nulle part.

Démonstration

Si y est rationnel, alors f(y) = 1. Pour montrer que la fonction n'est pas continue en y, il faut trouver un ε tel que peu importe la taille choisie pour ${\textstyle \delta }$ , il y aura des points z dans l'intervalle $]y-\delta ,y+\delta [$ tels que f(z) soit à l'extérieur de $]f(y)-\varepsilon ,f(y)+\varepsilon [\ =\ ]1-\varepsilon ,1+\varepsilon [$ . En fait, 1/2 est un tel ε : en effet, puisque les nombres irrationnels sont denses dans les nombres réels, peu importe la valeur choisie pour ${\textstyle \delta }$ , on pourra toujours trouver un z irrationnel dans $]y-\delta ,y+\delta [$ tel que f(z) = 0 est au moins éloigné de 1/2 par rapport à 1.
Si y est irrationnel, alors f(y) = 0. Encore une fois, on peut prendre ε = 1/2, et cette fois, puisque les nombres rationnels sont denses dans les réels, on peut choisir z pour être un nombre rationnel aussi proche de y que nécessaire. Encore une fois, f(z) = 1 est à plus de 1/2 de f(y) = 0 .

Ses restrictions à l'ensemble des nombres rationnels et à l'ensemble des nombres irrationnels sont constantes donc continues. La fonction de Dirichlet est donc un exemple archétypal du théorème de Blumberg.

La fonction de Dirichlet peut être construite comme la double limite ponctuelle d'une suite de fonctions continues :

\forall x\in \mathbb {R} ,\quad \mathbf {1} _{\mathbb {Q} }(x)=\lim _{k\to \infty }\left(\lim _{j\to \infty }\left(\cos(k!\,\pi \,x)\right)^{2j}\right)

où k et j sont des entiers. Cela montre que la fonction Dirichlet est une fonction de Baire de classe 2. Il ne peut pas s'agir d'une fonction de Baire de classe 1, car une telle fonction ne peut être discontinue que sur un ensemble maigre[2].

Périodicité

Pour tout nombre réel x et tout nombre rationnel strictement positif T, 1_ℚ(x + T) = 1_ℚ(x). La fonction de Dirichlet est donc un exemple de fonction périodique réelle qui n'est pas constante mais dont l'ensemble des périodes, l'ensemble des nombres rationnels, est une partie dense de ℝ.

Propriétés d'intégration

La fonction de Dirichlet n'est intégrable au sens de Riemann sur aucun segment de ℝ alors qu'elle y est bornée car l'ensemble de ses points de discontinuité n'est pas négligeable (pour la mesure de Lebesgue).
La fonction de Dirichlet fournit un contre-exemple montrant que le théorème de convergence monotone n'est pas vrai dans le cadre de l'intégrale de Riemann.

Démonstration

À partir d'une énumération de tous les nombres rationnels compris entre $0$ et $1$ , on définit la fonction $f n$ (pour tout entier naturel n) comme l'indicatrice de l'ensemble des $n$ premiers termes de cette suite de rationnels. La suite croissante des fonctions $f n$ (qui sont positives, Riemann-intégrables et d'intégrale nulle) converge alors simplement vers la fonction de Dirichlet, qui n'est pas Riemann-intégrable.

La fonction de Dirichlet est intégrable au sens de Lebesgue sur ℝ et son intégrale sur ℝ vaut 0 car elle est nulle sauf sur l'ensemble des nombres rationnels qui est négligeable (pour la mesure de Lebesgue).

Notes et références

Peter Gustav Lejeune Dirichlet, « Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données », Journal für die reine und angewandte Mathematik, vol. 4,‎ 1829, p. 157–169 (lire en ligne), et en particulier, p.169.
William Dunham, The Calculus Gallery, Princeton University Press, 2005, 197 p. (ISBN 0-691-09565-5)

Lien externe

(en) Eric W. Weisstein, « Dirichlet Function », sur MathWorld