Espérance conditionnelle

Un dé à six faces.

On considère le lancer d'un dé à six faces. On considère la variable aléatoire que l'on note A qui vaut 1 quand le résultat du lancer est pair (autrement 2, 4 ou 6), et 0 sinon. On considère aussi la variable B qui vaut 1 quand le résultat est premier (autrement dit, 2, 3 ou 5). Le tableau suivant reporte les valeurs de A et B.

L'espérance (non conditionnelle) de A vaut${\displaystyle E[A]=(0+1+0+1+0+1)/6=1/2}$. Par contre :

• L'espérance de A conditionné à l'événement B = 1 vaut ${\displaystyle E[A\mid B=1]=(1+0+0)/3=1/3}$.
• L'espérance de A conditionné à l'événement B = 0 vaut ${\displaystyle E[A\mid B=0]=(0+1+1)/3=2/3}$.
• L'espérance de B conditionné à l'événement A = 1 vaut ${\displaystyle E[B\mid A=1]=(1+0+0)/3=1/3}$.
• L'espérance de B conditionnée à A = 0 vaut${\displaystyle E[B\mid A=0]=(0+1+1)/3=2/3}$.

Soit B un événement de probabilité non nulle, on définit la probabilité conditionnelle ${\displaystyle \mathbb {P} (.|B)}$ ou ${\displaystyle \mathbb {P} _{B}}$ comme suit. Pour tout événement A : ${\displaystyle \mathbb {P} (A|B)={\frac {\mathbb {P} (A\cap B)}{\mathbb {P} (B)}}.}$

Si X est une variable aléatoire discrète d'espérance finie, on définit l'espérance de X sachant B, notée ${\displaystyle \mathbb {E} [X|B]}$, par[1] : ${\displaystyle \mathbb {E} [X|B]=\sum _{x_{i}}x_{i}\mathbb {P} _{B}(X=x_{i})={\frac {1}{\mathbb {P} (B)}}\sum _{x_{i}}x_{i}\mathbb {P} (\{X=x_{i}\}\cap B).}$

Si X est une variable aléatoire continue, d'espérance finie et de densité f, l'espérance de X sachant B est définie par ${\displaystyle \mathbb {E} [X|B]={\frac {1}{\mathbb {P} (B)}}\int _{X(B)}xf(x)dx.}$

De manière plus générale, si X est une variable aléatoire possédant une espérance, l’espérance de X conditionnée par B est[2] ${\displaystyle \mathbb {E} [X|B]={\frac {1}{\mathbb {P} (B)}}\int _{B}Xd\mathbb {P} ={\frac {1}{\mathbb {P} (B)}}\mathbb {E} [X.1_{B}],}$ où ${\displaystyle 1_{B}}$ est la fonction indicatrice de B qui est nulle sauf sur B où elle est constamment égale à 1.

Comme il existe une formule des probabilités totales, il existe une formule des espérances totales qui s'exprime ainsi[1]: si (B_i ) est une partition de l'univers formée d'événements de probabilité non nulle, alors : ${\displaystyle E[X]=\sum _{i}\mathbb {P} (B_{i})\mathbb {E} [X|B_{i}].}$

Espérance conditionnelle suivant plusieurs sous σ-algèbres: dans cet exemple l'espace de probabilité ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ est l'intervalle [0,1] avec la mesure de Lebesgue. On définit les σ-algèbres suivantes : ${\displaystyle {\mathcal {A}}={\mathcal {F}}}$; ${\displaystyle {\mathcal {B}}}$ la σ-algèbre générée par la subdivision 0, ¼, ½, ¾, 1; et ${\displaystyle {\mathcal {C}}}$ la σ-algèbre générée par la subdivision 0, ½, 1. Ici l'espérance conditionnelle est effectivement la moyenne sur la plus fine partition de la σ-algèbre.

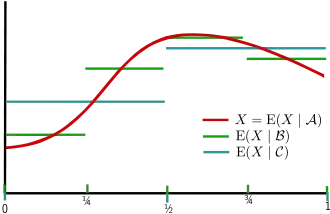
On peut, dans le cas des variables aléatoires de carré intégrable, interpréter l'espérance conditionnelle d'une variable aléatoire X comme la projection orthogonale de X sur l'espace vectoriel des variables aléatoires ${\displaystyle \ {\mathcal {G}}\ }$-mesurables, et, partant de là, comme la meilleure approximation qu'on puisse donner de la variable X à l'aide d'une variable aléatoire ${\displaystyle \ {\mathcal {G}}\ }$-mesurable. En effet, l'espérance conditionnelle possède la propriété suivante : pour toute variable aléatoire Y intégrable ${\displaystyle \ {\mathcal {G}}\ }$-mesurable,

${\displaystyle \mathbb {E} \left[(X-Y)^{2}\right]\ \geq \ \mathbb {E} \left[\left(X-\mathbb {E} \left[X|{\mathcal {G}}\right]\right)^{2}\right].}$

C'est-à-dire que, parmi les variables aléatoires Y intégrables ${\displaystyle \ {\mathcal {G}}\,}$-mesurables, la plus proche de X (pour la distance induite par le produit scalaire ${\displaystyle \ (X,Y)\mapsto \mathbb {E} \left[X\,Y\right]\ }$) est ${\displaystyle \ Y_{0}=\mathbb {E} \left[X|{\mathcal {G}}\right].\ }$

Pour ce qui est des applications, l'espérance conditionnelle pourra alors s'interpréter, par exemple, comme la meilleure prévision possible de la variable aléatoire X, en fonction de l'information disponible à un moment donné, information encodée par la tribu ${\displaystyle \ {\mathcal {G}},\ }$ ou encore comme la meilleure reconstruction du signal original X, après émission, en fonction de la déformation bruitée obtenu à la réception.

Il s'agit en ce sens de l'idée que l'on peut se faire du processus ${\displaystyle X}$ grâce à l'information ${\displaystyle {\mathcal {G}}}$, non par opposition au cas où l'on ne saurait rien de ce processus (information nulle), mais par rapport au cas où l'on connaitrait parfaitement ce dernier (information infinie). Une information conditionnelle correspond donc bel et bien à une perte d'information !

L’espérance conditionnelle possède les propriétés suivantes

• L’espérance conditionnelle est linéaire :

${\displaystyle \mathbb {E} \left[aX+bY|{\mathcal {G}}\right]\ =\ a\mathbb {E} \left[X|{\mathcal {G}}\right]+b\mathbb {E} \left[Y|{\mathcal {G}}\right]}$

• Son espérance vaut :

${\displaystyle \mathbb {E} \left[\mathbb {E} \left[X|{\mathcal {G}}\right]\right]\ =\ \mathbb {E} \left[X\right]}$

• Itération : si ${\displaystyle \ {\mathcal {H}}\subset {\mathcal {G}},}$

${\displaystyle \mathbb {E} \left[\mathbb {E} \left[X|{\mathcal {G}}\right]|{\mathcal {H}}\right]=\mathbb {E} \left[X|{\mathcal {H}}\right]}$

• Monotonie : Si ${\displaystyle \ X\leq Y,}$ alors

${\displaystyle \mathbb {E} \left[X|{\mathcal {G}}\right]\ \leq \ \mathbb {E} \left[Y|{\mathcal {G}}\right]}$

• Convergence monotone : si ${\displaystyle \ X_{n}\geq 0\ }$ est une suite croissante de variables aléatoires réelles qui converge presque sûrement vers X, alors

${\displaystyle \mathbb {E} \left[X_{n}|{\mathcal {G}}\right]\ {\underset {n\to \infty }{\longrightarrow }}\ \mathbb {E} \left[X|{\mathcal {G}}\right].}$

Plus généralement, le théorème de convergence dominée et le lemme de Fatou s'appliquent naturellement aux espérances conditionnelles.

• Indépendance: si X est indépendant de ${\displaystyle \ {\mathcal {G}},}$ alors

${\displaystyle \mathbb {E} \left[X|{\mathcal {G}}\right]\ =\ \mathbb {E} \left[X\right]}$

• Si Z est ${\displaystyle \ {\mathcal {G}}\,}$-mesurable, alors

${\displaystyle \mathbb {E} \left[XZ|{\mathcal {G}}\right]\ =\ Z\mathbb {E} \left[X|{\mathcal {G}}\right]}$

• Si X est ${\displaystyle \ {\mathcal {G}}\,}$-mesurable, alors

${\displaystyle \mathbb {E} \left[X|{\mathcal {G}}\right]\ =\ X}$

• Inégalité de Jensen : si ${\displaystyle \ \varphi \ }$ est une fonction convexe et ${\displaystyle \ \varphi (X)\ }$ est intégrable, alors

${\displaystyle \mathbb {E} \left[\varphi (X)|{\mathcal {G}}\right]\ \geq \ \varphi \left(\mathbb {E} \left[X|{\mathcal {G}}\right]\right)}$

• Espérance mathématique
• Probabilité conditionnelle
• Martingale (calcul stochastique)
• Théorème de la variance totale