Loi hypergéométrique

La loi hypergéométrique de paramètres associés $n$ , $p$ et $N$ est une loi de probabilité discrète, décrivant le modèle suivant :

On tire simultanément (ou successivement sans remise (mais cela induit un ordre))

n

boules dans une urne contenant

N_{1}=pN

boules gagnantes et

N_{2}=qN

boules perdantes (avec

q=1-p

, soit un nombre total de boules valant

pN+qN

N

). On compte alors le nombre de boules gagnantes extraites et on appelle

X

la variable aléatoire donnant ce nombre.

Loi hypergéométrique

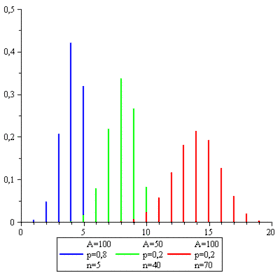Fonction de masse
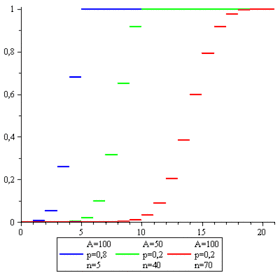Fonction de répartition

Paramètres	${\begin{aligned}N&\in 0,1,2,\dots \\p&\in [0;1]\\n&\in 0,1,2,\dots ,N\end{aligned}}\,$
Support	$\scriptstyle {k\,\in \,\max {(0,\,n-qN)},\,\dots ,\,\min {(pN,\,n)}}\,$
Fonction de masse	${\frac {{pN \choose k}{qN \choose n-k}}{N \choose n}}$
Espérance	$np\!$
Mode	$\left\lfloor (n+1){\frac {(pN+1)}{N+2}}\right\rfloor$
Variance	$npq{\frac {(N-n)}{(N-1)}}$
Asymétrie	${\frac {(N-2n)(q-p)(N-1)^{\frac {1}{2}}}{[npq(N-n)]^{\frac {1}{2}}(N-2)}}$
Kurtosis normalisé	$\scriptstyle {\frac {(N-1)[N^{2}(1-6pq)+N(1-6n)+6n^{2}]}{npq(N-n)(N-2)(N-3)}}$ $+{\frac {6N^{2}}{(N-2)(N-3)}}-6$
Fonction génératrice des moments	${\frac {{qN \choose n}\scriptstyle {\,_{2}F_{1}(-n,-pN;qN-n+1;e^{t})}}{N \choose n}}\,\!$
Fonction caractéristique	${\frac {{qN \choose n}\scriptstyle {\,_{2}F_{1}(-n,-pN;qN-n+1;e^{it})}}{N \choose n}}$

L'univers $X\!(\Omega )$ est l'ensemble des entiers de 0 à $n$ . La variable $X$ suit alors la loi de probabilité définie par[1]

\mathbb {P} (X=k)=\mathbb {P} _{X}(k)={\frac {{pN \choose k}{qN \choose n-k}}{N \choose n}}

(probabilité d'avoir

k

succès).

Cette loi de probabilité s'appelle la loi hypergéométrique de paramètres $(n,p,N)$ et l'on note $X\sim {\mathcal {H}}(n,p,N)$ .

Il est nécessaire que $p$ soit un réel compris entre 0 et 1, que $pN$ soit entier et que $n\leqslant N$ . Lorsque ces conditions ne sont pas imposées, l'ensemble des possibles $X\!(\Omega )$ est l'ensemble des entiers entre $\max(0,n-qN)$ et $\min(pN,n)$ .

Exemple simple

Un lac renferme une centaine de poissons dont un quart sont des brochets. On pêche 10 poissons ; la loi du nombre $X$ de brochets dans la prise est $H(10,1/4,100)$ .

On trouve alors pour les couples successifs $(k,\mathbb {P} (X=k))$ :

(0, 5%), (1, 18%), (2, 30%), (3, 26%), (4, 15%), (5, 5%), (6, 1%), (7, 0%), (8, 0%), (9, .0%), (10, 0%)

Donc un maximum de chances pour 2 ou 3 brochets. D'ailleurs, l'espérance du nombre de brochets vaut 10/4 = 2,5.

Calcul de la loi de probabilité

Il s'agit d'un tirage simultané (c'est-à-dire non ordonné et sans remise, même si la loi de probabilité resterait la même si l'on décidait d'ordonner le tirage car cela reviendrait à multiplier par $n!$ le numérateur et le dénominateur de la quantité $P(X=k)$ ) de $n$ éléments parmi $N$ , tirage que l'on considère comme équiprobable.

La combinatoire permet de dire que le cardinal de l'univers est $\textstyle {N \choose n}$ .

	Tirage	Resté dans l'urne	Total
Succès	$k$	$pN-k$	$pN$
Échecs	$n-k$	$qN-n+k$	$qN$
Total	$n$	$N-n$	$N$

L'évènement $\{X=k\}$ (voir tableau) représente le cas où l'on a tiré $k$ boules gagnantes parmi $pN$ et $n-k$ boules perdantes parmi $qN$ . Le cardinal de cet événement est donc $\textstyle {pN \choose k}{qN \choose n-k}$ .

La probabilité de l'évènement est donc $\mathbb {P} (X=k)=\mathbb {P} _{X}(k)={\frac {{pN \choose k}{qN \choose n-k}}{N \choose n}}$ .
Remarque : comme pour toute densité de probabilité, la somme des $\mathbb {P} (X=k)$ vaut 1, ce qui prouve l'identité de Vandermonde.

Espérance, variance et écart type

L'espérance d'une variable aléatoire $X$ suivant une loi hypergéométrique de paramètres $(n,p,N)$ , est la même que celle d'une variable binomiale de paramètres $(n,p)$ : $\mathbb {E} (X)=np\,$ .

Démonstration

On se donne : $X\sim {\mathcal {H}}(n,p,N)$

(si on se rapporte à un modèle d'urnes à tirage simultané, c'est-à-dire non ordonné et sans remise. On a donc $N_{N}=pN$ : le nombre de boules de type "réussite" et $N_{B}=qN=(1-p)N$ : le nombre de boules de type "échec".)

\mathbb {P} (X=k)={\frac {{N_{N} \choose k}{N_{B} \choose n-k}}{N \choose n}}

Numérotons de 1 à $N_{N}$ les boules de type "réussite" et définissons pour tout $k$ compris entre 1 et $N_{N}$ l'événement :

E_{k}=\{{\text{on a tiré parmi les  }}\ n\ {\text{  boules la boule de type réussite  }}\ k\}

Comme le nombre total $X$ de boules de type "réussite" tirées est $X=\sum _{k=1}^{N_{N}}\mathbf {1} _{E_{k}}\,$

(où $1$ est la fonction indicatrice de $E_{k}$ ), par linéarité de l'espérance, $\mathbb {E} (X)=N_{N}\mathbb {P} (E_{1})\,$ .

Évaluons maintenant $\mathbb {P} (E_{1})\,$ . En passant au complémentaire,

\mathbb {P} {\bar {(E_{1})}}={\frac {N-1 \choose n}{N \choose n}}={\frac {(N-1)!}{n!(N-1-n)!}}{\frac {n!(N-n)!}{N!}}={\frac {N-n}{N}}\,

qui est la probabilité de ne jamais tirer une boule donnée.

Donc $\mathbb {P} (E_{1})=1-{\frac {N-n}{N}}={\frac {n}{N}}={\frac {n}{N_{N}+N_{B}}}\,$

On en conclut donc que $\mathbb {E} (X)={\frac {nN_{N}}{N_{N}+N_{B}}}={\frac {nN_{N}}{N}}\,$

En rappelant que ${\frac {N_{N}}{N}}=p\,$ qui est exactement la probabilité d'avoir un succès, on a bien $\mathbb {E} (X)=np\,$ .

La variance d'une variable aléatoire suivant une loi hypergéométrique de paramètres $n,p,N$ est $npq{\frac {N-n}{N-1}}$ , dont on remarque qu'elle tend vers la variance $npq$ de la variable binomiale précédente lorsque $N$ tend vers l'infini.

L'écart type est alors ${\sqrt {npq}}{\sqrt {\frac {N-n}{N-1}}}$ .

Convergence

Lorsque $N$ tend vers l'infini, la loi hypergéométrique converge vers une loi binomiale de paramètres $n$ et $p$ . D'ailleurs, intuitivement, pour $N$ grand, tirer simultanément $n$ boules revient à effectuer $n$ fois une épreuve de Bernoulli dont la probabilité de succès serait $p$ ( $p$ est la proportion de boules gagnantes dans l'ensemble des boules), car il est très peu probable de retomber sur la même boule, même si on la replace dans l'urne.

Démonstration de la convergence vers la loi binomiale

Décomposons ${\frac {{pN \choose k}{qN \choose n-k}}{N \choose n}}$ .

{\frac {{pN \choose k}{qN \choose n-k}}{N \choose n}}={\frac {(pN)!}{k!(pN-k)!}}\cdot {\frac {(qN)!}{(n-k)!(qN-n+k)!}}\cdot {\frac {n!(N-n)!}{N!}}

={n \choose k}{\frac {(pN)!}{(pN-k)!}}\cdot {\frac {(qN)!}{(qN-n+k)!}}\cdot {\frac {(N-n)!}{N!}}

Pour le premier terme : ${\frac {(pN)!}{(pN-k)!}}={\frac {1\cdot 2\cdot 3\cdot ...\cdot pN}{1\cdot 2\cdot 3\cdot ...\cdot (pN-k)}}=pN\cdot (pN-1)\cdot ...\cdot (pN-k+1)$

Pour $N\rightarrow +\infty$ , on a :

{\frac {(pN)!}{(pN-k)!(pN)^{k}}}=\prod _{i=1}^{k}{\frac {pN-k+i}{pN}}=\prod _{i=1}^{k}(1+o(1))=1+o(1)

et l'on obtient ${\frac {pN!}{(pN-k)!}}\sim (pN)^{k}$

Le même raisonnement pour le second terme permet d'obtenir : ${\frac {(qN)!}{(qN-n+k)!}}\sim (qN)^{n-k}$ .

Enfin, pour le troisième terme : ${\frac {N!}{(N-n)!}}\sim N^{n}$ .

En conclusion, on a : ${\frac {{pN \choose k}{qN \choose n-k}}{N \choose n}}\sim _{N\rightarrow +\infty }{n \choose k}{\frac {(pN)^{k}(qN)^{n-k}}{N^{n}}}={n \choose k}p^{k}q^{n-k}$

Il s'agit bien d'une loi binomiale de paramètres $(n,p)$ .

En pratique, on peut approcher la loi hypergéométrique de paramètres $(n,p,N)$ par une loi binomiale de paramètres $(n,p)$ dès que $n/N<0,1$ , c'est-à-dire lorsque l'échantillon $n$ est 10 fois plus petit que la population $N$ .

Un exemple très classique de ce remplacement concerne les sondages. On considère fréquemment un sondage de $n$ personnes comme $n$ sondages indépendants alors qu'en réalité le sondage est exhaustif (on n'interroge jamais deux fois la même personne). Comme $n$ (nombre de personnes interrogées) < $N$ (population sondée)/10, cette approximation est légitime.

Origine de l'appellation hypergéométrique

L'appellation "loi hypergéométrique" vient du fait que sa série génératrice $E(x^{X})=\sum _{k=0}^{n}\mathbb {P} (X=k)x^{k}$ est un cas particulier de série hypergéométrique, série généralisant la série géométrique. En effet ${\frac {\mathbb {P} (X=k+1)}{\mathbb {P} (X=k)}}={\frac {(N_{1}-k)(n-k)}{(k+1)(N_{2}-n+k+1)}}$ est bien une fraction rationnelle en $k$ .

Lien externe

(en) Eric W. Weisstein, « Hypergeometric Distribution », sur MathWorld

Notes et références

(en) Jay L. Devore, Kenneth N. Berk et Matthew A. Carlton, Modern Mathematical Statistics with Applications, Springer International Publishing, coll. « Springer Texts in Statistics », 2021 (ISBN 978-3-030-55155-1 et 978-3-030-55156-8, DOI 10.1007/978-3-030-55156-8, lire en ligne)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.