Loi inverse-gamma

Dans la Théorie des probabilités et en statistiques, la distribution inverse-gamma est une famille de lois de probabilité continues à deux paramètres sur la demi-droite des réels positifs. Il s'agit de l'inverse d'une variable aléatoire distribuée selon une distribution Gamma.

Inverse-gamma
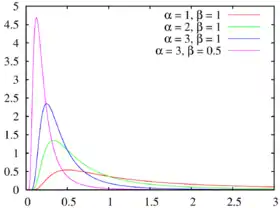Densité de probabilité


Fonction de répartition

Paramètres	$\alpha >0$ paramètre de forme (réel) $\beta >0$ paramètre d'échelle (réel)
Support	$x\in ]0;\infty [\!$
Densité de probabilité	${\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{-\alpha -1}\exp \left({\frac {-\beta }{x}}\right)$
Fonction de répartition	${\frac {\Gamma (\alpha ,\beta /x)}{\Gamma (\alpha )}}\!$
Espérance	${\frac {\beta }{\alpha -1}}\!$ pour $\alpha >1$
Mode	${\frac {\beta }{\alpha +1}}\!$
Variance	${\frac {\beta ^{2}}{(\alpha -1)^{2}(\alpha -2)}}\!$ pour $\alpha >2$
Asymétrie	${\frac {4{\sqrt {\alpha -2}}}{\alpha -3}}\!$ pour $\alpha >3$
Kurtosis normalisé	$6{\frac {5\,\alpha -11}{(\alpha -3)(\alpha -4)}}\!$ pour $\alpha >4$
Entropie	$\alpha \!+\!\ln(\beta \Gamma (\alpha ))\!-\!(1\!+\!\alpha )\psi (\alpha )$
Fonction génératrice des moments	${\frac {2\left(-\beta t\right)^{\!\!{\frac {\alpha }{2}}}}{\Gamma (\alpha )}}K_{\alpha }\left({\sqrt {-4\beta t}}\right)$
Fonction caractéristique	${\frac {2\left(-\mathrm {i} \beta t\right)^{\!\!{\frac {\alpha }{2}}}}{\Gamma (\alpha )}}K_{\alpha }\left({\sqrt {-4\mathrm {i} \beta t}}\right)$

Caractérisation

La densité de probabilité de la loi inverse-gamma est définie sur le support $x>0$ par:

f(x;\alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}(1/x)^{\alpha +1}\exp \left(-\beta /x\right)

où $\alpha$ est un paramètre de forme et $\beta$ un paramètre d'intensité, c'est-à-dire l'inverse d'un paramètre d'échelle.

F(x;\alpha ,\beta )={\frac {\Gamma (\alpha ,\beta /x)}{\Gamma (\alpha )}}\!

Si $X\sim {\mbox{Inv-Gamma}}(\alpha ,\beta )$ et $\alpha ={\frac {\nu }{2}},\beta ={\frac {1}{2}}$ alors $X\sim {\mbox{Inv-chi-square}}(\nu )\,$ est une loi inverse-χ²;
Si $X\sim {\mbox{Inv-Gamma}}(k,\theta )\,$ , alors $1/X\sim {\mbox{Gamma}}(k,1/\theta )\,$ la loi Gamma de paramètre de forme $k$ et de paramètre d'échelle $1/\theta$ (ou de manière équivalente, d'intensité $\theta$ );
Une généralisation multivariée de la loi inverse-gamma est la loi de Wishart inverse.

La densité de la loi Gamma est

f(x)=x^{k-1}{\frac {\mathrm {e} ^{-x/\theta }}{\theta ^{k}\,\Gamma (k)}}

et définissons la transformation $Y=g(X)={\frac {1}{X}}$ . La densité de la transformée est alors

f_{Y}(y)=f_{X}\left(g^{-1}(y)\right)\left|{\frac {\mathrm {d} }{\mathrm {d} y}}g^{-1}(y)\right|

={\frac {1}{\theta ^{k}\Gamma (k)}}\left({\frac {1}{y}}\right)^{k-1}\exp \left({\frac {-1}{\theta y}}\right){\frac {1}{y^{2}}}

={\frac {1}{\theta ^{k}\Gamma (k)}}\left({\frac {1}{y}}\right)^{k+1}\exp \left({\frac {-1}{\theta y}}\right)

={\frac {1}{\theta ^{k}\Gamma (k)}}y^{-k-1}\exp \left({\frac {-1}{\theta y}}\right)

Remplaçant $k$ par $\alpha$ , $\theta ^{-1}$ par $\beta$ et enfin $y$ par $x$ donne la densité donnée plus haut :

f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{-\alpha -1}\exp \left({\frac {-\beta }{x}}\right)

La loi du temps de premier contact (en) dans un processus de Wiener est une distribution de Lévy, qui est une loi inverse-gamma de paramètre $\alpha =0,5$ [1]

(en) Mike Ludkovski, « Math 526: Brownian Motion Notes », UC Santa Barbara, 2007, p. 5-6

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.