Ajustement de loi de probabilité

Différentes formes de la loi normale symétrique en fonction de la moyenne μ et de la variance σ ²

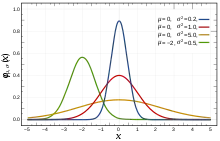
Le choix de la loi appropriée dépend de la présence ou de l'absence de symétrie de l'ensemble de données par rapport à la tendance centrale .

Lois asymétriques à droite

Asymétrie à gauche et à droite

Lorsque les valeurs les plus grandes ont tendance à être plus éloignées de la moyenne que les valeurs les plus petites, on a une loi asymétrique vers la droite (c'est-à-dire qu'il y a une asymétrie positive), on peut par exemple sélectionner la loi log-normale (c'est-à-dire les logarithmes des données sont normalement distribuées), la loi log-logistique (c'est-à-dire que les logarithmes des données suivent une loi logistique), la loi de Gumbel, la loi exponentielle, la loi de Pareto, la loi de Weibull, la loi de Burr ou la loi de Fréchet. Les quatre dernières lois sont bornées à gauche.

Les techniques d'ajustement de loi suivantes existent[2] :

• Méthodes paramétriques, par lesquelles les paramètres de la loi sont calculés à partir des séries de données[3]. Les méthodes paramétriques sont :
  • Méthode des moments
  • Estimation de l'espacement maximal (en)
  • Méthode des L-moments (en)[4]
  • Méthode du maximum de vraisemblance[5]

Répartition de Gumbel ajustée aux précipitations maximales d'un jour d'octobre au Suriname par la méthode de régression avec un intervalle de confiance supplémentaire à l'aide de CumFreq

• Diagramme quantile-quantile puis analyse de régression, utilisant une transformation de la fonction de répartition de sorte qu'une relation linéaire soit trouvée entre la répartition et les valeurs des données, qui peuvent également devoir être transformées, selon la loi de probabilité sélectionnée. Dans cette méthode, la répartition doit être estimée par la position du tracé[6]

Il est d'usage de transformer les données de manière logarithmique pour ajuster des lois symétriques (comme la normale et la logistique) aux données obéissant à une loi positivement asymétrique (c'est-à-dire asymétrique vers la droite, avec une moyenne supérieure au mode, et avec une queue à droite plus longue que la queue de gauche), voir la loi log-normale et la loi log-logistique. Un effet similaire peut être obtenu en prenant la racine carrée des données.

Pour ajuster une loi symétrique aux données obéissant à une loi biaisée négativement (c'est-à-dire biaisée vers la gauche, avec une moyenne inférieure mode, et avec une queue droite plus courte que la queue gauche), on pourrait utiliser les valeurs au carré des données pour accomplir l'ajustement.

Plus généralement, on peut élever les données à une puissance p afin d'ajuster des lois symétriques à des données obéissant à une loi d'asymétrie quelconque, où p < 1 lorsque l'asymétrie est positive et p > 1 lorsque l'asymétrie est négative. La valeur optimale de p doit être trouvée par une méthode numérique . La méthode numérique peut consister à supposer une plage de valeurs p, puis à appliquer la procédure d'ajustement de loi à plusieurs reprises pour toutes les valeurs p supposées, et enfin à sélectionner la valeur de p pour laquelle la somme des carrés des écarts des probabilités calculées à partir des fréquences mesurées (test du χ²) est minimum, comme c'est le cas dans CumFreq.

La généralisation améliore la flexibilité des lois de probabilité et augmente leur applicabilité dans l'ajustement de loi[6].

La polyvalence de la généralisation permet, par exemple, d'adapter des ensembles de données distribués approximativement normalement à un grand nombre de lois de probabilité différentes, tandis que des lois asymétriques négatives peuvent être ajustées à des lois de Gumbel invesée et du χ2
1.

(A) loi de probabilité de Gumbel inclinée vers la droite et (B) Gumbel réfléchie vers la gauche

Les lois asymétriques peuvent être réfléchies en remplaçant dans l'expression mathématique de la fonction de répartition (F) par son complément : F' = 1–F, obtenant la fonction de répartition complémentaire (également appelée fonction de survie) qui donne une image miroir. De cette manière, une loi asymétrique vers la droite est transformée en une loi asymétrique vers la gauche et vice versa.

La technique d'inversion d'asymétrie augmente le nombre de lois de probabilité disponibles pour l'ajustement de loi et élargit les opportunités d'ajustement de loi.

Certaines lois de probabilité, comme l' exponentielle, ne prennent pas en charge les valeurs de données (X) égales ou inférieures à zéro. Pourtant, lorsque des données négatives sont présentes, de telles lois peuvent toujours être utilisées en remplaçant X par Y = X – X_m, où X_m est la valeur minimale de X. Ce remplacement représente un déplacement de la lois de probabilité dans le sens positif, c'est-à-dire vers la droite, car X_m est négatif. Après avoir terminé l'ajustement de la loi de X, les valeurs X correspondantes sont trouvées à partir de X = Y + X_m, ce qui représente un décalage arrière de la loi dans le sens négatif, c'est-à-dire vers la gauche. La technique de déplacement de loi augmente les chances de trouver une loi de probabilité bien ajustée.

Loi composite (discontinue) avec intervalle de confiance[7]

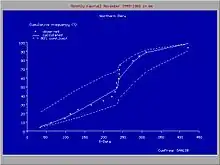
L'option existe d'utiliser deux loi de probabilité différentes, une pour la plage de données inférieure et une pour la plage supérieure, comme la loi de Laplace. Les plages sont séparées par un point d'arrêt. L'utilisation de telles loi de probabilité composites (discontinues) peut être opportune lorsque les données du phénomène étudié ont été obtenues dans deux ensembles de conditions différentes[6].

Analyse d'incertitude avec intervalle de confiance utilisant la loi binomiale[8]

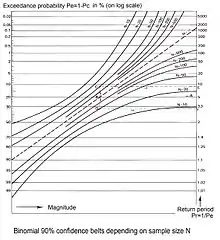
Les prévisions d'occurrence basées sur des lois de probabilité ajustées sont sujettes à l'incertitude, qui découle des conditions suivantes :

• La vraie loi de probabilité des événements peut s'écarter de la loi ajustée, car la série de données observées peut ne pas être totalement représentative de la probabilité réelle d'occurrence du phénomène en raison d'une erreur aléatoire
• L'occurrence d'événements dans une autre situation ou dans le futur peut s'écarter de la loi ajustée car cette occurrence peut également être sujette à une erreur aléatoire
• Un changement des conditions environnementales peut entraîner une modification de la probabilité d'occurrence du phénomène

Variations de neuf courbes de période de retour d'échantillons de 50 ans à partir d'un enregistrement théorique de 1 000 ans (ligne de base), données de Benson[9]

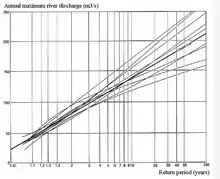
Une estimation de l'incertitude dans le premier et le second cas peut être obtenue avec la loi de probabilité binomiale en utilisant par exemple la probabilité de dépassement p_e (c'est-à-dire la chance que l'événement X soit supérieur à une valeur de référence X_r de X) et la probabilité de non-dépassement p_n (c'est-à-dire la probabilité que l'événement X soit inférieur ou égal à la valeur de référence X_r, on l'appelle aussi répartition). Dans ce cas, il n'y a que deux possibilités : soit il y a dépassement, soit il y a non-dépassement. Cette dualité est la raison pour laquelle la loi binomiale est applicable.

Avec la loi binomiale, on peut obtenir un intervalle de prédiction . Un tel intervalle estime également le risque d'échec, c'est-à-dire la probabilité que l'événement prédit reste toujours en dehors de l'intervalle de confiance. L'analyse de confiance ou de risque peut inclure la période de retour T = 1/p_e comme cela se fait en hydrologie.

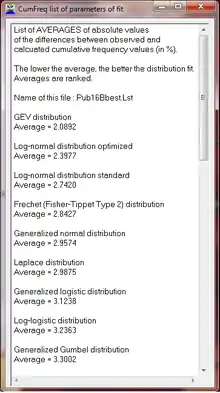
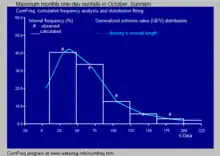
Liste des lois de probabilité classées par qualité d'ajustement selon CumFreq

Histogramme et densité de probabilité d'un ensemble de données correspondant à la loi d'extremum généralisée

En classant la qualité de l'ajustement des différentes lois, on peut se faire une idée de la loi qui est acceptable et de celle qui ne l'est pas.

À partir de la fonction de répartition, on peut dériver un histogramme et la fonction de densité.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Probability distribution fitting » (voir la liste des auteurs).

• Courbe d'ajustement
• Loi de mélange
• Loi produit (en)