Régression (statistiques)
En mathématiques, la régression recouvre plusieurs méthodes d’analyse statistique permettant d’approcher une variable à partir d’autres qui lui sont corrélées. Par extension, le terme est aussi utilisé pour certaines méthodes d’ajustement de courbe.
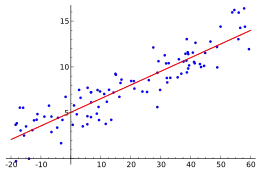
| Type |
Méthode statistique (d), analyse des données |
|---|---|
| Inventeur | |
| Nommé en référence à |
Regression Towards Mediocrity in Hereditary Stature (d) |
| Aspect de |
En apprentissage automatique, on distingue les problèmes de régression des problèmes de classification. Ainsi, on considère que les problèmes de prédiction d'une variable quantitative sont des problèmes de régression tandis que les problèmes de prédiction d'une variable qualitative sont des problèmes de classification. Certaines méthodes, comme la régression logistique, sont à la fois des méthodes de régression au sens où il s'agit de prédire la probabilité d'appartenir à chacune des classes et des méthodes de classification[1].
Histoire
Le terme provient de la régression vers la moyenne observée par Francis Galton au XIXe siècle : les enfants de personnes de grande taille avaient eux-mêmes une taille supérieure à celle de la population en moyenne, mais inférieure à celle de leurs parents (toujours en moyenne), sans que la dispersion de taille au sein de la population totale soit réduite pour autant[2] - [3]. Les techniques développées pour quantifier ce phénomène ont engendré des outils de mesure précieux dans tous les champs d’application des statistiques.
Contexte
On considère une population d’individus (êtres humains, animaux, pays, biens de consommation…) qui peuvent être décrits selon plusieurs critères appelés variables. Il peut s’agir de variables quantitatives (grandeurs numériques telles que la taille, l’âge, le prix, un pourcentage…) ou qualitatives (sexe, catégorie socio-professionnelle, saison, type de produit…)
Certaines variables peuvent être plus difficiles à mesurer que d’autres, pour des raisons techniques, des raisons d’accès (données publiques contre données privées), ou encore du fait d’un délai important entre la mise en place d’une expérience et son aboutissement. Il arrive donc que l’on souhaite estimer ces variables (dites expliquées) à partir des données plus faciles à obtenir (dites explicatives). On trouve aussi parfois les appellations variables dépendantes et indépendantes, mais elles présentent des risques de confusion avec la notion d’indépendance en probabilités, or les variables explicatives ne sont pas forcément mutuellement indépendantes[4].
La construction de la régression repose d’une part sur une modélisation des variables statistiques par des variables aléatoires (réelles ou non), d’autre part sur un recueil de données croisées, c’est-à-dire que pour un même échantillon de population, on dispose d’observations des différentes variables mesurées avec une imprécision éventuelle.
La régression consiste alors à formuler un indicateur sur les valeurs de la variable expliquée dépendant uniquement des valeurs des variables explicatives. Cet indicateur pourra ensuite être utilisé sur une population pour laquelle on ne connait que les valeurs des variables explicatives, afin d’estimer les valeurs de la variable expliquée.
Principe général
On distingue essentiellement deux cas selon la nature de la variable expliquée, représentée ici par une variable aléatoire Y. Les variables explicatives seront notées X1, … , Xn. Si certaines d’entre elles sont qualitatives, il est parfois judicieux de vectoriser leurs modalités[5] en distinguant une modalité de référence représentée par le vecteur nul, et en représentant les autres modalités par les vecteurs de base d’un espace euclidien. Sous certaines conditions, on peut aussi quantifier les modalités de ces variables.
Cas quantitatif
Pour une variable expliquée quantitative, c’est-à-dire lorsque Y est une variable aléatoire réelle, la fonction de régression est définie par un indicateur de la loi de Y conditionnellement aux valeurs des autres variables. Il s’agit le plus souvent de l’espérance conditionnelle[6] , mais on peut aussi considérer d’autres indicateurs de distribution conditionnelle comme la médiane ou d’autres quantiles, le mode, la variance[7]...
C’est donc une fonction numérique, dont les arguments sont des valeurs possibles des variables explicatives. Il est possible d’étendre cette définition au cas où certaines variables explicatives admettent une fonction de densité[8] conjointe avec la variable expliquée.
Cependant, la définition probabiliste ne suffit pas en général pour décrire la construction de l’indicateur à partir d’un jeu de données statistiques. En effet, les observations ne fournissent pas toujours toutes les combinaisons de modalités dans le cas de variables explicatives discrètes, et ne peuvent être exhaustives dans le cas de variables explicatives continues. La régression s’appuie alors sur un modèle de fonction avec un ou plusieurs paramètres, par exemple une fonction affine dans le cas de la régression linéaire ou multilinéaire. Mais d’autres modèles sont possibles.
On parle de modèle linéaire lorsque les paramètres apparaissent comme les coefficients d’une combinaison linéaire de fonctions de référence, comme dans le cas de la régression polynomiale ou pour des fonctions puissances ou exponentielles, quitte à passer par un changement de variable[9]… Mais certains modèles ne sont pas réductibles à un modèle linéaire et leur évaluation peut nécessiter des algorithmes spécifiques, voire recourir à une estimation non paramétrique[10].
Cas qualitatif
Pour une variable expliquée qualitative, la régression s’apparente aux problèmes de classification, au sens où l’on cherche à déterminer une modalité à partir des valeurs des autres variables.
La fonction de régression correspond dans ce cas à un partage de l’espace des valeurs des variables explicatives, par des méthodes géométriques ou par régression logistique.
Qualité de la régression
La variable expliquée ne s’identifie à la fonction de régression que dans le cas particulier d’une dépendance fonctionnelle. Dans le cas général, on peut interpréter la différence[11] comme une erreur aléatoire, souvent notée avec la lettre grecque ε (epsilon) : .
Si la fonction de régression est définie par l’espérance conditionnelle, le théorème de l'espérance totale assure alors que l’erreur est centrée. Le théorème de la variance totale donne l’égalité , ce qui permet de montrer que le rapport de corrélation défini par est inférieur à 1, et d’autant plus proche de 1 que la variance de Y conditionnellement à X est faible en moyenne, ce qui en fait un bon indicateur de la qualité de la régression. Inversement, lorsque le rapport de corrélation est proche de 0, cela signifie que la fonction de régression est pratiquement constante, donc que les variables explicatives apportent peu d’information sur l’espérance de la variable expliquée.
Le cas particulier d’une fonction de régression affine (avec une seule variable X) correspond à l’égalité entre le rapport de corrélation et le coefficient de corrélation linéaire .
Principaux modèles de régression
Le modèle de régression le plus connu est le modèle de régression linéaire.
Lorsque le modèle n'est pas linéaire, on peut effectuer une régression approchée par des algorithmes itératifs, on parle de régression non linéaire.
Si on s'intéresse au quantile conditionnel de la distribution de la variable aléatoire sachant le vecteur de variables aléatoires , on utilise un modèle de régression quantile[12] - [13].
Si la variable expliquée est une variable aléatoire binomiale, il est courant d'utiliser une régression logistique ou un modèle probit.
Si la forme fonctionnelle de la régression est inconnue, on peut utiliser un modèle de régression non paramétrique.
Voir aussi
- Interaction (statistiques)
- Régression linéaire
- Régression linéaire multiple
- Régression polynomiale
- Régression logistique
- Modèle linéaire généralisé
- Régression non paramétrique
- Modèles de régression multiple postulés et non postulés
- Régression circulaire
- Régression elliptique
- Régression locale
Références
- James et al. 2013, p. 28
- (en) Robert G. Mogull, Second-Semester Applied Statistics, Kendall/Hunt Publishing Company, (ISBN 0-7575-1181-3), p. 59
- Galton 1989
- Saporta 2011, p. 407
- Saporta 2011, §18.4 Discrimination sur variables quantitatives, p. 461
- Saporta 2011, p. 72
- Manski 1991
- Saporta 2011, §3.2 Extension à des variables quelconques, p. 77
- Saporta et 2011 p.389, §16.2 Ajustement sur des données
- Saporta 2011, §16.6 Régression non paramétrique, p. 404
- Dans certains cas, il est préférable de relier la variable expliquée avec la fonction de régression par un facteur multiplicatif, ce qui se ramène au cas additif par composition avec une fonction logarithme.
- (en) Roger Koenker et G. Bassett, « Regression quantiles », Econometrica, , p. 33-50
- (en) Roger Koenker, Quantile Regression, Cambridge University Press,
Bibliographie
- (en) Francis Galton, « Kinship and Correlation (reprinted 1989) », Statistical Science, Institute of Mathematical Statistics, vol. 4, no 2, , p. 80–86 (DOI 10.1214/ss/1177012581, JSTOR 2245330)
- (en) Charles Manski, « Regression », Journal of Economic Literature, vol. 29, no 1, , p. 34-50 (lire en ligne, consulté le )
- (en) Gareth James, Daniela Witten, Trevor Hastie et Robert Tibshirani, An Introduction to Statistical Learning, Springer Verlag, coll. « Springer Texts in Statistics »,
- Gilbert Saporta, Probabilités, analyse de données et Statistique, Paris, TECHNIP, , 622 p. (ISBN 978-2-7108-0980-7, lire en ligne), chapitres 16 à 18







