Régression logistique

Soit ${\displaystyle Y}$ la variable à prédire (variable expliquée) et ${\displaystyle X=(X_{1},X_{2},...,X_{J})}$ les variables prédictives (variables explicatives).

Dans le cadre de la régression logistique binaire, la variable ${\displaystyle Y}$ prend deux modalités possibles ${\displaystyle \{1,0\}}$. Les variables ${\displaystyle X_{j}}$ sont exclusivement continues ou binaires.

• Soit ${\displaystyle \Omega }$ un ensemble de ${\displaystyle n}$ échantillons, comportant ${\displaystyle n_{1}}$ (resp. ${\displaystyle n_{0}}$) observations correspondant à la modalité ${\displaystyle 1}$ (resp. ${\displaystyle 0}$) de ${\displaystyle Y}$.
• ${\displaystyle P(Y=1)}$ (resp. ${\displaystyle P(Y=0)}$) est la probabilité a priori pour que ${\displaystyle Y=1}$ (resp. ${\displaystyle Y=0}$). Pour simplifier, cela sera par la suite noté ${\displaystyle p(1)}$ (resp. ${\displaystyle p(0)}$).
• ${\displaystyle p(X\vert 1)}$ (resp. ${\displaystyle p(X\vert 0)}$) est la distribution conditionnelle des ${\displaystyle X}$ sachant la valeur prise par ${\displaystyle Y}$
• La probabilité a posteriori d'obtenir la modalité ${\displaystyle 1}$ de ${\displaystyle Y}$ (resp. ${\displaystyle 0}$) sachant la valeur prise par ${\displaystyle X}$ est notée ${\displaystyle p(1\vert X)}$ (resp. ${\displaystyle p(0\vert X)}$).

La régression logistique repose sur l’hypothèse fondamentale suivante, où l'on reconnaît la mesure nommée « évidence » ${\displaystyle Ev(p)=\ln {\frac {p}{1-p}}}$ popularisée par I.J. Good, E.T Jaynes et Myron Tribus pour les besoins de l'inférence bayésienne en évitant des renormalisations continuelles sur [0,1] :

${\displaystyle \ln {\frac {p(X\vert 1)}{p(X\vert 0)}}=a_{0}+a_{1}x_{1}+...+a_{J}x_{J}}$

où ${\displaystyle x_{1},x_{2},...,x_{J}}$ représentent les valeurs prises respectivement par les variables ${\displaystyle X_{1},X_{2},...,X_{J}}$.

Une vaste classe de distributions répondent à cette spécification, la distribution multinormale décrite en analyse discriminante linéaire par exemple, mais également d’autres distributions, notamment celles où les variables explicatives sont booléennes (0/1).

Par rapport à l’analyse discriminante toujours, ce ne sont plus les densités conditionnelles ${\displaystyle p(X\vert 1)}$ et ${\displaystyle p(X\vert 0)}$ qui sont modélisées mais le rapport de ces densités. La restriction introduite par l'hypothèse est moins forte.

La spécification ci-dessus peut être écrite de manière différente. On désigne par le terme LOGIT de ${\displaystyle p(1\vert X)}$ l’expression suivante

${\displaystyle \ln {\frac {p(1\vert X)}{1-p(1\vert X)}}=b_{0}+b_{1}x_{1}+...+b_{J}x_{J}}$

• Il s’agit bien d’une « régression » car on veut montrer une relation de dépendance entre une variable à expliquer et une série de variables explicatives.
• Il s’agit d’une régression « logistique » car la loi de probabilité est modélisée à partir d’une loi logistique.

En effet, après transformation de l’équation ci-dessus, nous obtenons

${\displaystyle p(1\vert X)={\frac {e^{b_{0}+b_{1}x_{1}+...+b_{J}x_{J}}}{1+e^{b_{0}+b_{1}x_{1}+...+b_{J}x_{J}}}}}$

Remarque : Équivalence des expressions

Nous sommes partis de deux expressions différentes pour aboutir au modèle logistique. Nous observons ici la concordance entre les coefficients ${\displaystyle a_{j}}$ et ${\displaystyle b_{j}}$. Reprenons le LOGIT

${\displaystyle \ln {\frac {p(1\vert X)}{1-p(1\vert X)}}=\ln {\frac {p(1\vert X)}{p(0\vert X)}}=\ln {\frac {p(1)p(X\vert 1)}{p(0)p(X\vert 0)}}=\ln {\frac {p(1)}{p(0)}}+\ln {\frac {p(X\vert 1)}{p(X\vert 0)}}}$

${\displaystyle \ln {\frac {p(1\vert X)}{1-p(1\vert X)}}=\ln {\frac {p(1)}{p(0)}}+a_{0}+a_{1}x_{1}+...+a_{J}x_{J}}$

Nous constatons que ${\displaystyle {\begin{cases}b_{0}=\ln {\frac {p(1)}{p(0)}}+a_{0}\\b_{j}=a_{j}&,j\geq 1\end{cases}}}$

À partir d’un fichier de données, nous devons estimer les coefficients ${\displaystyle b_{j}}$ de la fonction LOGIT. Il est très rare de disposer pour chaque combinaison possible des ${\displaystyle X_{j},\ (j=1,...,J)}$, même si ces variables sont toutes binaires, de suffisamment d’observations pour disposer d’une estimation fiable des probabilités ${\displaystyle P(1\vert X)}$ et ${\displaystyle P(0\vert X)}$. La méthode des moindres carrés ordinaire est exclue. La solution passe par une autre approche : la maximisation de la vraisemblance.

La probabilité d’appartenance d’un individu ${\displaystyle \omega }$ à un groupe, que nous pouvons également voir comme une contribution à la vraisemblance, peut être décrite de la manière suivante

${\displaystyle P(Y(\omega )=1\vert X(\omega ))^{Y(\omega )}\times [1-P(Y(\omega )=1\vert X(\omega ))]^{1-Y(\omega )}}$

La vraisemblance d’un échantillon ${\displaystyle \Omega }$ s’écrit alors :

${\displaystyle L=\prod _{\omega }P(Y(\omega )=1\vert X(\omega ))^{Y(\omega )}\times [1-P(Y(\omega )=1\vert X(\omega ))]^{1-Y(\omega )}}$

Les paramètres ${\displaystyle {\hat {b}}_{j}(j=0,...,J)}$ qui maximisent cette quantité sont les estimateurs du maximum de vraisemblance de la régression logistique.

Dans la pratique, les logiciels utilisent une procédure approchée pour obtenir une solution satisfaisante de la maximisation ci-dessus. Ce qui explique d’ailleurs pourquoi ils ne fournissent pas toujours des coefficients strictement identiques. Les résultats dépendent de l’algorithme utilisé et de la précision adoptée lors du paramétrage du calcul.

Dans ce qui suit, nous notons ${\displaystyle \beta \,}$ le vecteur des paramètres à estimer. La procédure la plus connue est la méthode Newton-Raphson qui est une méthode itérative du gradient (voir Algorithme d'optimisation). Elle s’appuie sur la relation suivante :

${\displaystyle \beta ^{i+1}=\beta ^{i}-\left({\frac {\partial ^{2}L}{\partial \beta \partial \beta '}}\right)^{-1}\times {\frac {\partial L}{\partial \beta }}}$

• ${\displaystyle \beta ^{i}\,}$ est la solution courante à l'étape ${\displaystyle i\,}$. ${\displaystyle \beta ^{0}=(0,...,0)\,}$ est une initialisation possible ;
• ${\displaystyle {\frac {\partial L}{\partial \beta }}\,}$ est le vecteur des dérivées partielles premières de la vraisemblance ;
• ${\displaystyle {\frac {\partial ^{2}L}{\partial \beta \partial \beta '}}\,}$ est la matrice des dérivées partielles secondes de la vraisemblance ;
• les itérations sont interrompues lorsque la différence entre deux vecteurs de solutions successifs est négligeable.

Cette dernière matrice, dite matrice hessienne, est intéressante car son inverse représente l’estimation de la matrice de variance covariance de ${\displaystyle \beta \,}$. Elle sera mise en contribution dans les différents tests d’hypothèses pour évaluer la significativité des coefficients.

Sous forme matricielle : ${\displaystyle {\overrightarrow {\beta _{i+1}}}={\overrightarrow {\beta _{i}}}+\left(^{t}XWX\right)^{-1}{}^{t}X\left({\overrightarrow {y}}-{\overrightarrow {p}}\right)}$

L’objectif étant de produire un modèle permettant de prédire avec le plus de précision possible les valeurs prises par une variable catégorielle ${\displaystyle Y}$, une approche privilégiée pour évaluer la qualité du modèle serait de confronter les valeurs prédites avec les vraies valeurs prises par ${\displaystyle Y}$ : c’est le rôle de la matrice de confusion. On en déduit alors un indicateur simple, le taux d’erreur ou le taux de mauvais classement, qui est le rapport entre le nombre de mauvaises prédictions et la taille de l’échantillon.

Lorsque la matrice de confusion est construite sur les données qui ont servi à élaborer le modèle, le taux d’erreur est souvent trop optimiste, ne reflétant pas les performances réelles du modèle dans la population. Pour que l’évaluation ne soit pas biaisée, il est conseillé de construire cette matrice sur un échantillon à part, dit échantillon de test. Par opposition à l’échantillon d’apprentissage, il n’aura pas participé à la construction du modèle.

Le principal intérêt de cette méthode est qu’elle permet de comparer n’importe quelle méthode de classement et sélectionner ainsi celle qui s’avère être la plus performante face à un problème donné.

Il est possible d’exploiter un schéma probabiliste pour effectuer des tests d’hypothèses sur la validité du modèle. Ces tests reposent sur la distribution asymptotique des estimateurs du maximum de vraisemblance.

Pour vérifier la significativité globale du modèle, nous pouvons introduire un test analogue à l’évaluation de la régression linéaire multiple. L’hypothèse nulle s’écrit ${\displaystyle H_{0}:b_{1}=b_{2}=\dots =b_{J}=0}$, que l’on oppose à l’hypothèse alternative ${\displaystyle H_{1}}$ : un des coefficients au moins est non nul

La statistique du rapport de vraisemblance s’écrit ${\displaystyle \Lambda =2\times [l(J+1)-l(1)]}$, elle suit une loi du ${\displaystyle \chi ^{2}}$ à ${\displaystyle J}$ degrés de libertés.

• ${\displaystyle l(J+1)}$ est le logarithme de la vraisemblance du modèle avec l’ensemble des variables (donc J+1 coefficients en comptant la constante) et,
• ${\displaystyle l(1)}$ le logarithme de la vraisemblance du modèle réduit à la seule constante.

Si la probabilité critique (la p-value) est inférieure au niveau de signification que l’on s’est fixé, on peut considérer que le modèle est globalement significatif. Reste à savoir quelles sont les variables qui jouent réellement un rôle dans cette relation.

Dans le cas où l’on cherche à tester le rôle significatif d’une variable. Nous réalisons le test suivant ${\displaystyle H_{0}:b_{j}=0}$, contre ${\displaystyle H_{1}:b_{j}\neq 0}$.

La statistique de WALD répond à ce test, elle s’écrit ${\displaystyle W={\frac {{\hat {b}}^{2}}{{\hat {V}}({\hat {b}})}}}$, elle suit une loi du ${\displaystyle \chi ^{2}}$ à ${\displaystyle 1}$ degré de liberté.

N.B. : La variance estimée du coefficient ${\displaystyle {\hat {b}}_{j}}$ est lue dans l’inverse de la matrice hessienne vue précédemment.

Les deux tests ci-dessus sont des cas particuliers du test de significativité d’un bloc de coefficients. Ils découlent du critère de la « déviance » qui compare la vraisemblance entre le modèle courant et le modèle saturé (le modèle dans lequel nous avons tous les paramètres).

L’hypothèse nulle s’écrit dans ce cas ${\displaystyle H_{0}:\beta (q)=0}$, où ${\displaystyle \beta (q)}$ représente un ensemble de ${\displaystyle q\,}$ coefficients simultanément à zéro.

La statistique du test ${\displaystyle W(q)=2\times [l(J+1)-l(J+1-q)]}$ suit une loi du ${\displaystyle \chi ^{2}}$ à ${\displaystyle q}$ degrés de libertés.

Ce test peut être très utile lorsque nous voulons tester le rôle d’une variable explicative catégorielle à ${\displaystyle q+1}$ modalités dans le modèle. Après recodage, nous introduisons effectivement ${\displaystyle q}$ variables indicatrices dans le modèle. Pour évaluer le rôle de la variable catégorielle prise dans son ensemble, quelle que soit la modalité considérée, nous devons tester simultanément les coefficients associés aux variables indicatrices.

D’autres procédures d’évaluation sont couramment citées s’agissant de la régression logistique. Nous noterons entre autres le test de Hosmer-Lemeshow qui s’appuie sur le « score » (la probabilité d’affectation à un groupe) pour ordonner les observations. En cela, elle se rapproche d’autres procédés d’évaluation de l’apprentissage telles que les courbes ROC qui sont nettement plus riches d’informations que la simple matrice de confusion et le taux d’erreur associé.

Les résultats sont consignés dans le tableau suivant.

Résultats de l'exécution de la régression logistique sur le fichier de données

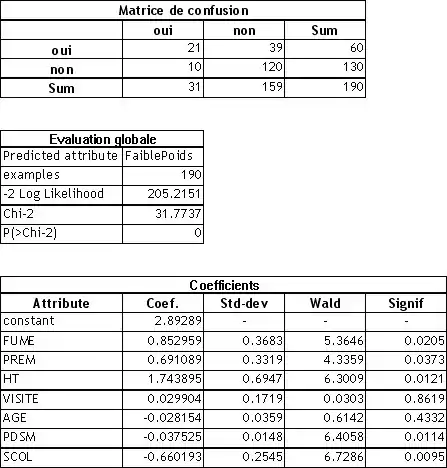
• Dans la matrice de confusion, nous lisons que sur les données en apprentissage, le modèle de prédiction réalise 10 + 39 = 49 mauvaises prédictions. Le taux d’erreur en resubstitution est de 49/190 = 25,78 %
• La statistique du rapport de vraisemblance LAMBDA est égale à 31.77, la probabilité critique associée est 0. Le modèle est donc globalement très significatif, il existe bien une relation entre les variables explicatives et la variable expliquée.
• En étudiant individuellement les coefficients liés à chaque variable explicative, au risque de 5 %, nous constatons que FUME, PREM et HT sont néfastes au poids du bébé à la naissance (entraînent un faible poids du bébé) ; PDSM et SCOL en revanche semblent jouer dans le sens d’un poids plus élevé du bébé. VISITE et AGE ne semblent pas jouer de rôle significatif dans cette analyse.

Cette première analyse peut être affinée en procédant à une sélection de variables, en étudiant le rôle concomitant de certaines variables, etc. Le succès de la régression logistique repose justement en grande partie sur la multiplicité des outils d’interprétations qu’elle propose. Avec les notions d’odds, d’odds ratios et de risque relatif, calculés sur les variables dichotomiques, continues ou sur des combinaisons de variables, le statisticien peut analyser finement les causalités et mettre en évidence les facteurs qui pèsent réellement sur la variable à expliquer.

Pour classer un nouvel individu ${\displaystyle \omega \,}$, nous devons appliquer la règle de Bayes :

${\displaystyle Y(\omega )=1\,}$ ssi ${\displaystyle P(Y(\omega )=1\vert X(\omega ))>P(Y(\omega )=0\vert X(\omega ))\,}$

Qui est équivalent à

${\displaystyle Y(\omega )=1\,}$ ssi ${\displaystyle P(Y(\omega )=1\vert X(\omega ))>0.5\,}$

Si nous considérons la fonction LOGIT, cette procédure revient à s’appuyer sur la règle d’affectation :

${\displaystyle Y(\omega )=1\,}$ ssi ${\displaystyle {\hat {b}}_{0}+{\hat {b}}_{1}\times X_{1}(\omega )+...+{\hat {b}}_{J}\times X_{J}(\omega )>0\,}$

Prenons l’observation suivante ${\displaystyle X(\omega )\,}$ = (FUME = 1 « oui » ; PREM = 1 « un prématuré dans l’historique de la mère » ; HT = 0 « non » ; VISITE = 0 « pas de visite chez le médecin pendant le premier trimestre de grossesse » ; AGE = 28 ; PDSM = 54.55 ; SCOL = 2 « entre 12 et 15 ans »).

En appliquant l’équation ci-dessus, nous trouvons ${\displaystyle 2.893+0.853\times 1+0.691\times 1+1.744\times 0+0.030\times 0-0.028\times 28-0.038\times 54.55-0.660\times 2=0.28125}$. Le modèle donc prédit un bébé de faible poids pour cette personne.

Ce qui est justifié puisqu’il s’agit de l’observation n°131 de notre fichier, et elle a donné lieu effectivement à la naissance d’un enfant de faible poids.

La règle d’affectation ci-dessus est valide si l’échantillon est issu d’un tirage au hasard dans la population. Ce n’est pas toujours le cas. Dans de nombreux domaines, nous fixons au préalable les effectifs des classes ${\displaystyle Y=1}$ et ${\displaystyle Y=0}$, puis nous procédons au recueil des données dans chacun des groupes. On parle alors de tirage rétrospectif. Il est dès lors nécessaire de procéder à un redressement. Si les coefficients associés aux variables de la fonction logit ne sont pas modifiés, la constante en revanche doit être corrigée en tenant compte des effectifs dans chaque classe (${\displaystyle n_{1}}$ et ${\displaystyle n_{0}}$) et des vraies probabilités a priori ${\displaystyle p(1)}$ et ${\displaystyle p(0)}$ (cf. les références ci-dessous).

• Ricco Rakotomalala, Pratique de la régression logistique
• M. Bardos, Analyse Discriminante - Application au risque et scoring financier, Dunod, 2001. (chapitre 3)
• Bernard, P.-M., "Analyse des tableaux de contingence en épidémiologie", Les Presses de l'Université du Québec, 2004
• Bouyer J., Hémon D., Cordier S., Derriennic F., Stücker I., Stengel B., Clavel J., Épidémiologie - Principes et méthodes quantitatives, Les Éditions INSERM, 1993
• Hosmer D.W., Lemeshow S., Applied logistic regression, Wiley Series in Probability and Mathematical Statistics, 2000
• Kleinbaum D.G., Logistic regression. A self-learning text, Springer-Verlag, 1994.
• Kleinbaum D.G., Kupper L.L., Muller E.M., Applied regression analysis and other multivariate methods, PWS-KENT Publishing Company, Boston, 1988.
• J.P. Nakache, J. Confais, Statistique Explicative Appliquée, Technip, 2003 (Partie 2)
• Pierre-François Verhulst, « Recherches mathématiques sur la loi d'accroissement de la population », Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres de Bruxelles, n^o 18,‎ 1845, p. 1-42 (lire en ligne [PDF], consulté le 18 octobre 2009)
• André de Palma et Jacques-François Thisse, « Les modèles de choix discrets », Annales d'Economie et de Statistique,‎ 1989 (lire en ligne)
• (en) Thierry Magnac, « logit models of individual choice », dans Steven Durlauf et Lawrence Blume, The New Palgrave Dictionary of Economics, Palgrave Macmillan, 2008 (lire en ligne)
• (en) Ken Train, Discrete Choice Methods with Simulation, Cambridge University Press, 30 juin 2009, 2^e éd., 408 p. (ISBN 978-0-521-74738-7, lire en ligne), p. 34-75 (Chapitre 3)
• (en) Andrew Gelman et Jennifer Hill, Data Analysis Using Regression And Multilevel/Hierarchical Models, Cambridge University Press, coll. « Analytical Methods for Social Research », 18 décembre 2006, 1^re éd., 648 p. (ISBN 978-0-521-68689-1, lire en ligne) (Chapitre 5)

• Modèle de Verhulst
• Modèle probit