Analyse discriminante linéaire

L’objectif est de produire une règle d’affectation ${\displaystyle X(\omega )\mapsto Y(\omega )}$ qui permet de prédire, pour une observation ${\displaystyle \omega }$ donnée, sa valeur associée de Y à partir des valeurs prises par X.

La règle bayesienne consiste à produire une estimation de la probabilité a posteriori d’affectation

${\displaystyle P(Y=y_{k}~|~X)={\frac {P(Y=y_{k})\times P(X~|~Y=y_{k})}{\sum _{i=1}^{K}P(Y=y_{i})\times P(X~|~Y=y_{i})}}}$

${\displaystyle P(Y=y_{k})}$ est la probabilité a priori d’appartenance à une classe. ${\displaystyle P(X~|~Y=y_{k})}$ représente la fonction de densité des X conditionnellement à la classe ${\displaystyle y_{k}}$.

La règle d’affectation pour un individu ${\displaystyle \omega }$ à classer devient alors ${\displaystyle Y(\omega )=\arg \max _{k}\ P(Y=y_{k}~|~X(\omega ))}$. Toute la problématique de l’analyse discriminante revient alors à proposer une estimation de la quantité ${\displaystyle P(X~|~Y=y_{k})}$

On distingue principalement deux approches pour estimer correctement la distribution ${\displaystyle P(X~|~Y=y_{k})}$ :

• L’approche non-paramétrique n’effectue aucune hypothèse sur cette distribution mais propose une procédure d’estimation locale des probabilités, au voisinage de l’observation ${\displaystyle \omega \,}$ à classer. Les procédures les plus connues sont la méthode d'estimation par noyau et la méthode des plus proches voisins. La principale difficulté est de définir de manière adéquate le voisinage.

• La seconde approche effectue une hypothèse sur la distribution des nuages de points conditionnels, on parle dans ce cas d’analyse discriminante paramétrique. L’hypothèse la plus communément utilisée est sans aucun doute l’hypothèse de multinormalité (voir loi normale).

Dans le cas de la loi normale multidimensionnelle, la distribution des nuages de points conditionnels s’écrit :

${\displaystyle f_{k}(X)=P(X~|~Y=y_{k})={\frac {1}{(2\pi )^{j/2}\times |W_{k}|^{1/2}}}\times e^{-{\frac {1}{2}}\,^{t}(X-\mu _{k})W_{k}^{-1}(X-\mu _{k})}}$

où ${\displaystyle |W_{k}|}$ représente le déterminant de la matrice de variance covariance conditionnellement à ${\displaystyle y_{k}}$.

L’objectif étant de déterminer le maximum de la probabilité a posteriori d’affectation, nous pouvons négliger tout ce qui ne dépend pas de ${\displaystyle k}$. En appliquant le logarithme à la relation de Bayes, nous obtenons le score discriminant proportionnel à ${\displaystyle \ln[P(Y=y_{k}~|~X)]}$ :

${\displaystyle D(Y=y_{k},X)=2\ln[P(Y=y_{k})]-\ln |W_{k}|-\,^{t}(X-\mu _{k})W_{k}^{-1}(X-\mu _{k})}$

La règle d’affectation devient donc ${\displaystyle Y(\omega )=\arg \max _{k}D(Y=y_{k},X(\omega ))}$.

Si l’on développe complètement le score discriminant, nous constatons qu’il s’exprime en fonction du carré et du produit croisé entre les variables prédictives. On parle alors d’analyse discriminante quadratique. Très utilisée en recherche car elle se comporte très bien, en matière de performances, par rapport aux autres méthodes, elle est moins répandue auprès des praticiens. En effet, l’expression du score discriminant étant assez complexe, il est difficile de discerner clairement le sens de la causalité entre les variables prédictives et la classe d’appartenance. Il est notamment malaisé de distinguer les variables réellement déterminantes dans le classement, l’interprétation des résultats est assez périlleuse.

Une seconde hypothèse permet de simplifier encore les calculs, c’est l’hypothèse d’homoscédasticité : les matrices de variances covariances sont identiques d’un groupe à l’autre. Géométriquement, cela veut dire que les nuages de points ont la même forme (et volume) dans l’espace de représentation.

La matrice de variance covariance estimée est dans ce cas la matrice de variance covariance intra-classes calculée à l’aide de l’expression suivante :

${\displaystyle W={\frac {1}{n-K}}\sum _{k}n_{k}\times W_{k}}$

De nouveau, nous pouvons évacuer du score discriminant tout ce qui ne dépend plus de ${\displaystyle k}$, il devient :

${\displaystyle D(Y=y_{k},X)=2\ln[P(Y=y_{k})]-\,^{t}(X-\mu _{k})W^{-1}(X-\mu _{k})}$

En développant l’expression du score discriminant après introduction de l’hypothèse d’homoscédasticité, on constate qu’elle s’exprime linéairement par rapport aux variables prédictives.

Nous disposons donc d’autant de fonctions de classement que de modalités de la variable à prédire, ce sont des combinaisons linéaires de la forme suivante :

${\displaystyle \left\{{\begin{matrix}D(y_{1},X)=a_{0}+a_{1}\times X_{1}+\dots +a_{J}\times X_{J}\\D(y_{2},X)=b_{0}+b_{1}\times X_{1}+\dots +b_{J}\times X_{J}\\\dots \end{matrix}}\right.}$

Cette présentation est séduisante à plus d’un titre. Il est possible, en étudiant la valeur et le signe des coefficients, de déterminer le sens des causalités dans le classement. De même, il devient possible, comme nous le verrons plus loin, d’évaluer le rôle significatif des variables dans la prédiction.

Les hypothèses de multinormalité et d’homoscédasticité peuvent sembler trop contraignantes, restreignant la portée de l’analyse discriminante linéaire dans la pratique.

La notion clé qu’il faut retenir en statistique est la notion de robustesse. Même si les hypothèses de départ ne sont pas trop respectées, une méthode peut quand même s’appliquer. C’est le cas de l’analyse discriminante linéaire. Le plus important est de le considérer comme un séparateur linéaire. Dans ce cas, si les nuages de points sont séparables linéairement dans l’espace de représentation, elle peut fonctionner correctement.

Par rapport aux autres techniques linéaires telles que la régression logistique, l’analyse discriminante présente des performances comparables. Elle peut être lésée néanmoins lorsque l’hypothèse d’homoscédasticité est très fortement violée.

De manière classique en apprentissage supervisé, pour évaluer les performances d'une fonction de classement, nous confrontons ses prédictions avec les vraies valeurs de la variable à prédire sur un fichier de données. Le tableau croisé qui en résulte s’appelle une matrice de confusion avec : en ligne les vraies classes d’appartenance, en colonne les classes d’appartenance prédites. Le taux d’erreur ou taux de mauvais classement est tout simplement le nombre de mauvais classement, lorsque la prédiction ne coïncide pas avec la vraie valeur, rapporté à l’effectif du fichier de données.

Le taux d’erreur a de séduisant qu’il est d’interprétation aisée, il s’agit d’un estimateur de la probabilité de se tromper si l’on applique la fonction de classement dans la population.

Attention cependant, on parle de taux biaisé ou taux d'erreur en résubstitution, le taux d’erreur mesuré sur les données qui ont servi à construire la fonction de classement. Tout simplement parce que les données sont juges et parties dans ce schéma. La bonne procédure serait de construire la fonction de classement sur une fraction des données, dites d'apprentissage ; puis de l’évaluer sur une autre fraction de données, dite de test. Le taux d’erreur en test ainsi mesuré est un indicateur digne de foi.

La pratique veut que la répartition des données en apprentissage et test soit de 2/3 – 1/3. Mais en réalité, il n’y a pas de règle véritable. Le plus important est de concilier deux exigences contradictoires : en avoir suffisamment en test pour obtenir une estimation stable de l’erreur, tout en réservant suffisamment en apprentissage pour ne pas pénaliser la méthode d’apprentissage.

Lorsque les effectifs sont faibles, et que le partage apprentissage-test des données n’est pas possible, il existe des méthodes de ré-échantillonnage telles que la validation croisée ou le bootstrap pour évaluer l’erreur de classement.

Le taux d’erreur permet d’évaluer et de comparer des méthodes, quelles que soient leurs hypothèses sous-jacentes. Dans le cas de l’analyse discriminante linéaire, nous pouvons exploiter le modèle probabiliste pour réaliser des tests d’hypothèses.

Un premier test permet de répondre à la question suivante : est-il possible de discerner les nuages de points dans l’espace de représentation. Rapporté dans le cadre multinormal, cela revient à vérifier si les centres de gravité conditionnels sont confondus (hypothèse nulle) ou si un au moins de ces centres de gravité s’écarte significativement des autres (hypothèse alternative).

La statistique du test est le ${\displaystyle \lambda }$ de Wilks, son expression est la suivante :

${\displaystyle \lambda ={\frac {|W|}{|V|}}}$

où ${\displaystyle |W|}$ représente le déterminant de la matrice de variance covariance intra-classes, ${\displaystyle |V|}$ le déterminant de la matrice de variance covariance globale.

La table des valeurs critiques de la loi de Wilks étant rarement disponible dans les logiciels, on utilise couramment les transformations de Bartlett et de Rao qui suivent respectivement une loi du KHI-2 et de Fisher.

Avec un prisme différent, nous constatons que ce test peut s’exprimer comme une généralisation multidimensionnelle de l’analyse de variance à un facteur (ANOVA), on parle dans ce cas de MANOVA (Multidimensional Analysis of Variance).

Comme dans toutes les méthodes linéaires, il est possible d’évaluer individuellement chaque variable prédictive, et éventuellement d’éliminer celles qui ne sont pas significatives dans la discrimination.

La statistique du test s’appuie sur la variation du Lambda de Wilks lors de l'adjonction de la (J+1)-ième variable dans le modèle de prédiction. Sa formule est la suivante :

${\displaystyle F={\frac {n-K-J}{K-1}}\times \left({\frac {\lambda _{J}}{\lambda _{J+1}}}-1\right)}$

Elle suit une loi de Fisher à ${\displaystyle (K-1,n-K-J)}$ degrés de liberté.

Une analyse discriminante linéaire a été lancée sur les Flea Beetles décrites dans l'article analyse discriminante. Les résultats sont les suivants.

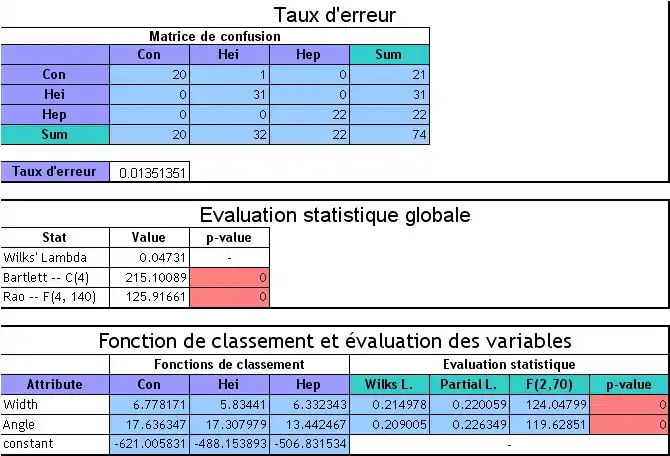
• La matrice de confusion indique qu'une seule erreur a été commise, un « Concinna » a été classé en « Heikertingeri ». Le taux d'erreur associé est de 1,35 %. Ce résultat est à relativiser, il a été établi sur les données ayant servi à l'apprentissage.

• Les centres de gravité des trois nuages de points s'écartent significativement. C'est ce que nous indique la statistique de Wilks dans la section MANOVA. Les probabilités critiques associées, transformation de Bartlett et de Rao, sont proches de 0. Ce résultat numérique confirme l'impression visuelle laissée par la projection des nuages de points dans l'espace de représentation (voir Analyse discriminante).

• La variable à prédire comportant 3 modalités, nous obtenons 3 fonctions de classement linéaires. L'évaluation individuelle des variables dans la discrimination indique qu'elles sont toutes les deux très significatives (p-value proches de 0).

Pour classer une nouvelle observation avec les coordonnées (Width = 150 et Angle = 15), nous appliquons les fonctions de la manière suivante.

• Con : ${\displaystyle 6{,}778171\times 150+17{,}636347\times 15-621{,}005831=660{,}265024}$
• Hei : ${\displaystyle 5{,}83441\times 150+17{,}307979\times 15-488{,}153893=646{,}627292}$
• Hep : ${\displaystyle 6{,}332343\times 150+13{,}442467\times 15-506{,}831534=644{,}656921}$

Sur la base de ces calculs, nous affectons à cette observation la classe « Concinna ».