Somme de Minkowski
En géométrie, la somme de Minkowski est une opération sur les parties d'un espace vectoriel. À deux parties A et B elle associe leur ensemble somme, formé des sommes d'un élément de A et d'un élément de B :
La somme de deux compacts est compacte. Il est ainsi possible de restreindre l'opération à cet ensemble, qui peut être muni d'une distance, dite de Hausdorff. La somme de Minkowski est alors une opération continue. De plus elle respecte les convexes, c'est-à-dire que la somme de deux convexes est encore convexe. La mesure de la somme de deux convexes vérifie une majoration, dite inégalité de Brunn-Minkowski.
La somme de Minkowski intervient dans de nombreux domaines des mathématiques pures ou appliquées. Cet outil est à la base de nombreuses démonstrations de théorèmes isopérimétriques, visant à déterminer la partie de l'espace de plus vaste volume possible, la contrainte étant la donnée de la mesure de sa frontière. En géométrie euclidienne, on trouve les sphères de dimension n. La somme de Minkowski intervient aussi pour le comptage du nombre de face d'un polyèdre, résoudre des questions de pavages ou encore pour étudier la géométrie des convexes. Ils sont appliqués par exemple en cristallographie pour des raisons de pavages d'espace, en économie pour optimiser les productions possibles d'un groupe d'entreprises, ou encore pour étudier les mélanges.
Préambule
Exemples
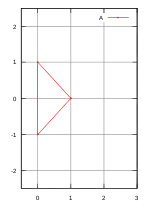
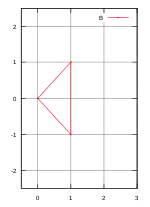
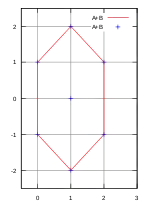
L'ensemble de A à gauche est un triangle dont les coordonnées des sommets sont (0,-1), (0,1) et (1,0). À droite est illustré un triangle semblable B, orienté différemment. Les coordonnées sont (0,0), (1,-1) et (1,1). Si les ensembles A et B sont deux triplets, on trouve :
Si A et B sont les triangles illustrés en rouge, on trouve un hexagone, illustré par la figure en bas à droite.
De manière générale, la somme de deux polygones est encore un polygone. Cette propriété est vraie pour un polyèdre de dimension quelconque.
On peut remarquer l'analogie entre la somme de Minkowski et le produit de convolution. De manière imagée, on peut obtenir la surface de la somme A + B de deux ensembles en couvrant B de peinture et en faisant parcourir à son centre la surface A. Pour cette raison, cette somme de Minkowski est parfois appelée convolution de A et de B.
De manière évidente, la somme d'un ensemble A et d'un singleton {b} correspond à la translation de A par le vecteur b.
Il n'est guère plus complexe de se rendre compte que la somme de deux carrés est encore un carré. D'une manière plus générale, si C est un convexe, symétrique par rapport à l'origine, la somme C + C est égal au convexe 2C, ici 2C désigne l'homothétie de rapport 2. La démonstration est un peu plus subtile, elle est analogue au lemme préliminaire utilisé dans la démonstration du théorème de Minkowski. Pour s'en rendre compte, on peut remarquer que tout élément de 2C est élément de C + C, réciproquement soit u + v un élément de C + C, il s'écrit aussi comme le double de 1/2(u + v), or cet élément est dans C.
On peut citer un dernier exemple, que l'on trouve dans l'article théorème isopérimétrique. Soient C un compact convexe d'un plan euclidien et P un polygone convexe dont les sommets sont tous sur la frontière de C et dont la plus grande arête est d'une longueur majorée par ε. Alors la somme de P et du disque de centre le vecteur nul et de rayon ε contient le compact convexe C. Cette propriété est une étape pour établir qu'il n'existe aucune surface d'aire plus grande que le disque de même périmètre.
Premières propriétés
Cette opération est commutative, associative, possède pour élément neutre le singleton {0}. Elle est en outre distributive par rapport à la réunion
- .
D'un point de vue topologique
- la somme de deux parties ouvertes est ouverte (comme réunion de translatées de B par exemple)
- la somme de deux parties compactes est compacte (par le théorème de Bolzano-Weierstrass dans le cas métrisable, ou comme image continue du produit de deux compacts dans un groupe topologique quelconque)
- la somme de deux parties convexes est convexe
- la somme, restreinte aux ensembles non vides fermés et bornés est une opération semi-continue supérieurement (cf Distance de Hausdorff).
Remarque : La somme de deux parties fermées n'est pas nécessairement fermée : par exemple en prenant dans le plan la droite des abscisses et l'hyperbole xy = 1, leur somme forme le plan privé d'une droite. Cependant, la somme d'un fermé et d'un compact est fermée.
Formule de Steiner-Minkowski
Dimension 2
.jpg.webp)
La formule de Steiner a été découverte pour démontrer le théorème isopérimétrique. En dimension 2, il stipule que si C est une surface de périmètre p, alors son aire est plus petite que celle du disque de périmètre p. Si le périmètre p n'est pas fini, comme pour un compact construit à l'aide d'une courbe de Koch, la formule reste exacte, mais ne possède plus aucun intérêt. Le théorème prend la forme suivante :
l'égalité n'étant obtenue que dans le cas où le compact C est un disque.
Pour le démontrer, une approche consiste à étudier l'aire de la somme de Minkowski d'un convexe compact C et de tB, où t désigne un réel positif et B le disque unité. On trouve l'égalité suivante, si μ est la fonction volume qui à C associe son aire, et C est un ensemble convexe :
La fonction volume μ est définie de manière très générale, elle correspond à la mesure de Lebesgue, qui à un carré de côté 1 associe 1. Le périmètre d'une courbe est définie à la manière de Jordan, c'est-à-dire qu'il est égal à la borne supérieure des longueurs de lignes polygonales approximant la frontière. Sous cette forme, démontrer le théorème isopérimétrique revient à montrer que le polynôme du second degré, qui à t associe μ(C + t.B), possède un discriminant positif, ou encore que le polynôme admet une racine réelle.
Cette formule permet aussi d'obtenir une expression du périmètre p — toujours si C est convexe — en fonction de φ :
Dimension quelconque
Il est tentant de généraliser la formule, dans un espace euclidien E de dimension n. On peut considérer la mesure du volume sC1 + tC2, où C1 et C2 sont deux compacts convexes et s et t deux réels positifs. On obtient une expression polynomiale du type :
Les coefficients Vk s'appellent volumes mixtes de C1 et C2[1].
On dispose de quelques égalités évidentes :
Une autre est un peu plus délicate à démontrer dans le cas où C2 est égal à B :
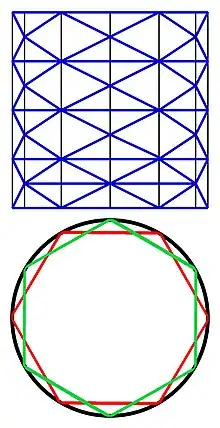
Ici, n–1 désigne le volume (n – 1)-dimensionnel. Définir une mesure (n – 1)-dimensionnelle devient subtil. Une première méthode consiste à généraliser la technique utilisée en dimension 1, pour un arc rectifiable. Elle demande d'être adaptée et est spécifique aux convexes. La mesure de la surface est alors la borne supérieure des convexes polyédriques inclus dans C1. La convexité est indispensable, sinon le contre-exemple de droite montre que la définition n'a pas de sens. La surface que l'on souhaite mesurer est un cylindre, le polyèdre utilisé est un lampion dont les sommets sont situés sur des hexagones chaque fois décalés d'un douzième de tour. Si les plans des hexagones se rapprochent de plus en plus, la surface du polyèdre augmente jusqu'à l'infini[2]. Une autre technique consiste à utiliser une forme différentielle et plus précisément une forme volume. La difficulté réside alors dans le fait que la surface d'un convexe n'a pas de raison d'être une variété de classe C1. Il devient nécessaire d'utiliser des espaces comparables à ceux de Sobolev pour définir la surface[3].
Les volumes mixtes vérifient une majoration utilisée pour démontrer le théorème isopérimétrique pour les dimensions supérieures à 2. Elle porte le nom d'inégalité d'Alexandrov-Fenchel[4] :
Inégalité de Brunn-Minkowski
Démontrée par Hermann Brunn[5] et Hermann Minkowski[6] dans le cas où les deux compacts sont convexes, puis dans le cas général par Lazar Lusternik[7] - [8], l'inégalité de Brunn-Minkowski est une minoration du volume de la somme de deux parties compactes d'un espace euclidien :
Soient E un espace euclidien de dimension n, μ la mesure de Lebesgue sur E et A et B deux compacts non vides de E. L'inégalité suivante est vérifiée[9] - [10] :
.
Si les deux compacts A et B sont convexes et homothétiques, il y a égalité.
Notes et références
- B. Teissier, Volumes des corps convexes, géométrie et algèbre, Institut de Mathématiques de Jussieu. Leçon donnée le jeudi 7 octobre 1999, Rédigée par C. Reydy, p. 8.
- Cet exemple est tiré de Marcel Berger et Bernard Gostiaux, Géométrie différentielle : variétés, courbes et surfaces [détail des éditions] p. 226.
- Pour plus de détails, voir : (en) Herbert Federer, Geometric Measure Theory, Springer-Verlag, 1969 (ISBN 978-3-540-60656-7), 3.2.37, 3.2.39, 3.2.26.
- (en) A. D. Alexandrov, Selected Works, CRC, 2002 (ISBN 2881249841).
- (de) H. Brunn, Über Ovale und Eiflächen, Munich, (thèse).
- (de) Hermann Minkowski, Geometrie der Zahlen, Leipzig, Teubner, .
- (de) Lazar A. Lyusternik, « Die Brunn–Minkowskische Ungleichnung für beliebige messbare Mengen », C.R. Acad. Sci. URSS, vol. 8, , p. 55-58.
- Bernard Maurey, « Inégalité de Brunn-Minkowski-Lusternik, et autres inégalités géométriques et fonctionnelles », Séminaire Bourbaki, t. 46, 2003-2004, p. 95-114 (lire en ligne).
- (en) Jiří Matoušek, Lectures on Discrete Geometry [détail des éditions], p. 297.
- Frank Barthe, « L’inégalité de Brunn-Minkowski », sur Images des mathématiques, .
- Elle s'inspire directement d'une généralisation en dimension n de celle-ci, en dimension 2 : (en) A. Treibergs, Inequalities that Imply the Isoperimetric Inequality, Université d'Utah, p. 16.
- Une démonstration en dimension n est proposée à : (en) R. J. Gardner, « The Brunn-Minkowski inequality », dans Bull. (New Series) Amer. Math. Soc., vol. 39, n° 3, 2002, p. 363.
(en) Bernard Dacorogna, Introduction to the Calculus of Variations, Imperial College Press, 2004 (ISBN 1860945082)
Voir aussi
Articles connexes
- Convolution
- Inégalité de Prékopa-Leindler (en)
- Inégalité de Brunn-Minkowski inverse de Milman (en)
- Inégalité de Brunn-Minkowski aléatoire de Vitale (en)
- Lemme de Shapley-Folkman (en)
- Théorème de Barbier
- Théorème de Minkowski
- Théorème de Steinhaus
- En morphologie mathématique, la somme de Minkowski sert à définir la dilatation.
Lien externe
M. Rousset, Sommes de Minkowski de triangles, Thèse de troisième cycle, Université Joseph Fourier, 1996









![{\displaystyle \forall i\in [1,n-1]\quad V_{k}(C_{1},C_{2})^{2}\leq V_{k-1}(C_{1},C_{2})V_{k+1}(C_{1},C_{2})}](https://img.franco.wiki/i/3bd7422e9f7702ea1b5288206d77664f9953a5d8.svg)

.jpg.webp)

![{\displaystyle ]0,1]}](https://img.franco.wiki/i/37ba32ee265793ab3329dad45b38f4f4b7457b68.svg)
![]0,1[](https://img.franco.wiki/i/6f6a83a50a400fb17f0c9abe6e674c6526a7b0e1.svg)
![\forall t\in ]0,1]\quad f(t)=(1+\lambda )^{{{\frac 1n}}}2^{{{\frac {n-1}n}}}-\lambda ^{{{\frac 1n}}}-1\;](https://img.franco.wiki/i/6298d45f5e889d027546f7d51defc27cde08fa71.svg)
![\forall t\in ]0,1[\quad f'(t)={\frac 1n}\left(\left({\frac 2{1+\lambda }}\right)^{{{\frac {n-1}n}}}-\left({\frac 1{\lambda }}\right)^{{{\frac {n-1}n}}}\right)={\frac 1{n\lambda ^{{{\frac {n-1}n}}}}}\left(\left({\frac {2\lambda }{1+\lambda }}\right)^{{{\frac {n-1}n}}}-1\right)<0](https://img.franco.wiki/i/d16f8762d0bb904d60af14b9bfbe620617527af6.svg)













