Semi-continuité

En analyse mathématique, la semi-continuité est une propriété des fonctions définies sur un espace topologique et à valeurs dans la droite réelle achevée ℝ = ℝ ∪ ${-\infty, +\infty}$ ; il s'agit d'une forme faible de la continuité. Intuitivement, une telle fonction $f$ est dite semi-continue supérieurement en $x 0$ si, lorsque $x$ est proche de $x 0$ , $f (x)$ est soit proche de $f (x 0)$ , soit inférieur à $f (x 0)$ . Pour définir semi-continue inférieurement, on remplace « inférieur à » par « supérieur à » dans la définition précédente.

Exemples

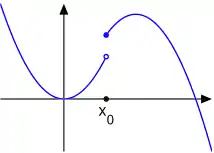
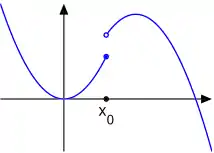
Une fonction semi-continue supérieurement (le point complètement bleu indique f(x₀)).

Une fonction semi-continue inférieurement (le point complètement bleu indique f(x₀)).

Considérons la fonction f définie par f(x) = 0 pour x ≠ 0 et f(0) = 1. Cette fonction est semi-continue supérieurement, mais non semi-continue inférieurement. Plus généralement, la fonction caractéristique d'une partie A d'un espace topologique est semi-continue supérieurement si et seulement si A est fermé et semi-continue inférieurement si et seulement si A est ouvert.

La fonction partie entière f(x) = ⌊x⌋, qui retourne le plus grand entier inférieur ou égal au x donné, est semi-continue supérieurement.

La fonction f définie par f(x) = sin(1/x) pour x ≠ 0 et f(0) = 1 est semi-continue supérieurement (mais n'admet pas de limite à gauche ni à droite en 0).

La fonction de répartition d'une variable aléatoire réelle est semi-continue supérieurement.

L'application rang (taille du plus grand mineur non nul), de M_m,n(ℝ) dans ℝ, est semi-continue inférieurement, mais pas supérieurement, sauf aux points où elle atteint sa valeur maximum, min(m, n).

L'application longueur d'un arc dans un espace métrique E, ou plus généralement variation totale $V I (f)$ d'une fonction $f$ d'un ensemble totalement ordonné $I$ dans E, est semi-continue inférieurement, sur l'espace de fonctions bornées $B (I, E)$ (muni de la topologie de la convergence uniforme). Cela signifie exactement que pour tout réel positif $r$ , la partie $\{f\in B(I,E)\mid V_{I}(f)\leq r\}$ est fermée dans $B (I, E)$ .

Définitions formelles

Soit $X$ un espace topologique, $x 0$ un point de $X$ et $f$ une fonction de $X$ dans ℝ.

Semi-continuité supérieure

On dit que $f$ est semi-continue supérieurement en $x 0$ si :

pour tout $t>f(x_{0})$ , il existe un voisinage $U$ de $x 0$ tel que $\forall x\in U,~f(x)\leq t~;$

Si on est dans un espace métrique, la propriété suivante suffit :

$\limsup _{x\to x_{0}}f(x)\leq f(x_{0})$ , où $lim sup$ désigne la limite supérieure d'une fonction en un point.

La fonction $f$ est dite semi-continue supérieurement si l'une des propriétés équivalentes suivantes est vérifiée :

$f$ est semi-continue supérieurement en tout point de $X$ ;
pour tout réel $α$ , l'ensemble de sur-niveau $\{x\in X\mid f(x)\geq \alpha \}$ est fermé ;
l'hypographe $\{(x,\alpha )\in X\times \mathbb {R} \mid f(x)\geq \alpha \}$ est fermé.

Semi-continuité inférieure

Les notions de semi-continuité inférieure d'une fonction se définissent de manière analogue, par symétrie car elles reviennent aux notions correspondantes de semi-continuité supérieure de la fonction opposée.

On dit que $f$ est semi-continue inférieurement en $x 0$ si :

pour tout $t<f(x_{0})$ , il existe un voisinage $U$ de $x 0$ tel que $\forall x\in U,~f(x)\geq t~;$

Si on est dans un espace métrique, la propriété suivante suffit :

$\liminf _{x\to x_{0}}f(x)\geq f(x_{0})$ , où $lim inf$ désigne la limite inférieure d'une fonction en un point.

La fonction $f$ est dite semi-continue inférieurement si l'une des propriétés équivalentes suivantes est vérifiée :

$f$ est semi-continue inférieurement en tout point de $X$ ;
pour tout réel $α$ , l'ensemble de sous-niveau $\{x\in X\mid f(x)\leq \alpha \}$ est fermé ;
l'épigraphe $\{(x,\alpha )\in X\times \mathbb {R} \mid f(x)\leq \alpha \}$ est fermé.

En analyse convexe, où l'épigraphe d'une fonction joue un rôle particulier (il est convexe si et seulement si la fonction est convexe), une fonction semi-continue inférieurement est dite « fermée » (parce que son épigraphe est fermé), mais la notion d'application fermée en topologie générale est différente.

Propriétés

Une fonction est continue en un point si et seulement si elle est semi-continue supérieurement et inférieurement en ce point.

Une fonction est semi-continue inférieurement si et seulement si, considérée comme fonction à valeurs dans ℝ muni de la topologie stricte à droite, elle est continue[1] (la semi-continuité supérieure se caractérise de même à l'aide de la topologie stricte à gauche).

Si f et g sont deux fonctions semi-continues supérieurement (resp. inférieurement) en x₀, alors f + g l'est aussi. Si de plus les deux fonctions sont à valeurs positives ou nulles, leur produit fg est également semi-continu supérieurement (resp. inférieurement) en x₀. Le produit d'une fonction semi-continue supérieurement par un réel négatif est une fonction semi-continue inférieurement.

La borne supérieure $f$ d'une famille $(f i) i \in I$ de fonctions semi-continues inférieurement de X dans ℝ est semi-continue inférieurement. En effet, pour tout réel $α$ , l'ensemble

$\{x\in X\mid f(x)>\alpha \}=\left\{x\in X~\left|~\sup _{i\in I}f_{i}(x)>\alpha \right.\right\}=\bigcup _{i\in I}\{x\in X\mid f_{i}(x)>\alpha \}$

est une réunion d'ouverts, donc un ouvert.

Par contre, même si toutes les fonctions $f i$ sont continues, $f$ n'est pas nécessairement continue : en fait, sur un espace uniforme, toute fonction semi-continue inférieurement est le sup d'une famille de fonctions continues (si X est un espace métrique, cette famille peut même être choisie dénombrable, donc toute fonction réelle semi-continue sur X est de classe de Baire 1).

Si C est un compact (par exemple un intervalle fermé [a, b] de ℝ) ou même seulement un espace dénombrablement compact et si f : C → ℝ est semi-continue supérieurement, alors f est majorée sur C et atteint sa borne supérieure. La propriété est analogue pour la borne inférieure d'une fonction semi-continue inférieurement. Ces propriétés généralisent le théorème des bornes.

Semi-continuité faible

Dans le cas où $X$ est un espace vectoriel topologique, on dit que la fonction $f$ est faiblement semi-continue (inférieurement ou supérieurement) lorsque la limite dans la définition de semi-continuité est prise au sens de la topologie faible. Afin d'éviter les ambiguïtés, on écrira parfois fortement semi-continue pour désigner la semi-continuité définie pour la topologie forte.

Note et référence

Claude Berge, Espaces topologiques : Fonctions multivoques, vol. 3, Dunod, 1966, 2^e éd., p. 80.

Article connexe

Théorème d'insertion de Katětov-Tong (en)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.