Intensité acoustique

Le son perçu en un point ne donne pas d'indication sur la direction de provenance, la comparaison entre deux points est nécessaire pour cela.

L'acoustique, dans sa définition d'origine, a pour objet l'étude des sons perçus par les humains. La grandeur physique la plus en rapport avec cette perception est la pression acoustique ; mais celle-ci ne concerne qu'un point de l'espace, et ne donne aucune indication sur la façon dont la vibration de l'air qui constitue le son s'est transmise.

Pour décrire utilement l'espace sonore il faut donner, pour chaque point et à chaque instant, non seulement la pression acoustique, mais aussi la direction du mouvement des petits volumes d'air qui, en vibrant, constituent le son[3].

Le concept d'intensité acoustique s'est progressivement précisé, au cours de l'histoire de la discipline, d'un sens général lié à la perception des sons (la sonie) en une description de la transmission de l'énergie mécanique par les ondes sonores.

Toutes les études acoustiques où on cherche à déterminer la transmission des sons utilisent l'intensité acoustique :

• acoustique architecturale, quand il s'agit de faire entendre certains sons à une audience, et d'éviter d'en transmettre d'autres ;
• acoustique environnementale, quand il s'agit de déterminer les sources de bruit et de contrôler la diffusion des nuisances sonores ;
• industries automobile et aéronautique, pour la réduction du bruit à l'intérieur et à l'extérieur des moyens de transport ;
• en acoustique musicale lorsqu'on étudie la genèse des sons des instruments ;
• exploration des milieux par le sonar et l'échographie, tant industrielle que médicale.

L'action du son sur notre ouïe exige une certaine puissance.

L'intensité acoustique, quand on la définit de cette manière, relie l'acoustique aux autres sciences par l'application d'un principe général: le premier principe de la thermodynamique, qui prévoit la conservation de l'énergie.

L'onde sonore transporte une puissance, qui peut connaître des pertes par transformation en chaleur, mais pas d'accroissement. Les pertes sont assez faibles, c'est pourquoi le son se transmet au loin ; dans une première approximation, on peut les négliger.

Toute la puissance sonore mesurée en un point a une origine (actuelle ou passée) dans un flux d'énergie provenant d'une ou plusieurs directions repérables. L'intensité acoustique mesure le flux résultant de ces transferts.

En physique, la puissance se définit comme la quantité d'énergie par unité de temps fournie par un système. En mécanique, elle est le produit de l'application d'une force par la vitesse du déplacement de l'objet auquel elle s'applique. En acoustique, cette force créée par l'onde sonore s'applique à une unité de surface du front sonore, dont on peut réduire arbitrairement la taille pour décrire un endroit précis du champ sonore.

Le son est une vibration de l'air[4]. Comme l'air est compressible, cette vibration est à la fois un déplacement et une compression alternatifs. Dans une direction donnée, distinguons un sens qui définit un « avant » et un « arrière ». L'air se déplace (très faiblement) vers l'« avant » : il comprime la zone qui se trouve dans cette direction. Puis il revient vers sa position médiane et la dépasse vers l'« arrière », créant, pour la zone qui se trouve de l'autre côté, une dépression. Cette vibration est progressive : le petit déplacement local du milieu autour d'une position se transmet à la zone voisine, à une certaine vitesse, jusqu'à de grandes distances.

La force par unité de surface s'appelle la pression acoustique, et s'exprime en pascals (ou newtons par mètre carré), de symbole Pa (ou N m⁻²). Elle varie selon la position ${\displaystyle {\vec {x}}}$ dans la propagation de l'onde sonore et selon le temps ${\displaystyle t}$, aussi la note-t-on ${\displaystyle p({\vec {x}},t)}$. Le déplacement, caractérisé par la vitesse acoustique ${\displaystyle {\vec {v}}({\vec {x}},t)}$[5], dépend de l'élasticité et de la masse du milieu. Le produit des deux est l'intensité acoustique instantanée de l'onde sonore, toujours par unité de surface :

L'intensité acoustique, par rapport à une direction de référence, est égale à la moyenne temporelle de p.v.cos θ, où θ est l'angle entre la direction de propagation de l'onde sonore et la direction de référence

${\displaystyle {\vec {I}}_{i}({\vec {x}},t)=p({\vec {x}},t)\,{\vec {v}}({\vec {x}},t)}$

Produit d'un vecteur (la vitesse) par un scalaire (la pression), cette grandeur est un vecteur ; elle possède une norme, un sens et une direction[6].

L'intensité acoustique en un point est la moyenne dans le temps de l'intensité acoustique instantanée :

${\displaystyle {\vec {I}}({\vec {x}})=\langle {\vec {I}}_{i}({\vec {x}},t)\rangle ={\frac {1}{T}}\int _{0}^{T}p.{\vec {v}}\,\mathrm {d} t.}$

La moyenne est prise sur un temps suffisamment long, par rapport à la plage de fréquence considérée, pour que la moyenne ait une valeur stable, mais sur un temps suffisamment court pour que cette moyenne mobile puisse suivre les variations d'intensité acoustique[7].

En champ libre, c'est-à-dire si aucune variation du milieu ne s'oppose à la propagation de l'onde, la pression et la vitesse varient ensemble.

Pour comprendre le son, les acousticiens s'attachent à étudier le transfert de cette énergie. Ils forment l'hypothèse que dans les conditions ordinaires, les phénomènes sonores sont linéaires, et que donc le principe de superposition permet de les étudier un par un.

On va donc considérer pour commencer une onde sonore unique, se propageant sans aucune perturbation.

Pour une onde plane sinusoïdale, la pression acoustique est une petite variation positive ou négative de la pression atmosphérique, écart qui varie en ${\displaystyle p_{0}.\sin \omega t}$. De son côté, la vitesse acoustique en un point est également un écart par rapport à la vitesse locale du vent, et varie positivement ou négativement en ${\displaystyle {\vec {v}}_{0}.\sin(\omega t+\varphi )}$. L'intensité acoustique instantanée, qui est produit de la pression par la vitesse, varie donc en :

${\displaystyle p_{i}.{\vec {v}}_{i}=p_{0}.{\vec {v}}_{0}.\sin(\omega t).\sin(\omega t+\varphi )=p_{0}.{\vec {v}}_{0}\left(\sin ^{2}(\omega t).\cos \varphi +\sin(\omega t).\cos(\omega t).\sin \varphi \right)}$

L'intensité acoustique est la moyenne temporelle de l'intensité acoustique instantanée. Dans le calcul de cette moyenne, seul intervient le terme en sin², la moyenne de l'autre étant nulle. L'intensité acoustique est donc égale à :

${\displaystyle \langle p_{i}.{\vec {v}}_{i}\rangle ={1 \over 2}.p_{0}.{\vec {v}}_{0}.\cos \varphi }$

Pour une onde progressive, elle est positive si l'élévation de pression correspond à un déplacement de l'air vers l'avant, comme c'est le cas si l'axe des x est dans le sens de la progression de l'onde, dans le cas contraire, elle est négative. En revanche, elle est nulle si les deux grandeurs sont déphasées, ce qui est le cas pour une onde stationnaire.

Le flux de l'intensité acoustique instantanée à travers une surface S donnée correspond à l'énergie acoustique E transférée à travers cette surface, à l'instant considéré :

${\displaystyle E_{i}=\int _{S}{\vec {I}}_{i}.{\overrightarrow {\mathrm {d} S}}}$

En particulier, le flux d'intensité acoustique sortant d'une surface fermée entourant une source correspond à l'énergie acoustique produite par cette source.

L'énergie sonore transférée à travers cette même surface est la moyenne temporelle de l'énergie acoustique instantanée. Il faut prendre garde sur ce point que la moyenne du flux de l'intensité acoustique (énergie transmise) n'est pas égale au flux de la moyenne, parce que les contributions instantanées des différents points de la surface peuvent aller en sens opposé. L'égalité n'est vérifiée que si la surface est en tout point perpendiculaire à la direction de l'intensité acoustique.

Schéma de flux

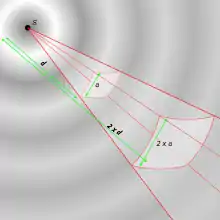
L'intensité acoustique représente le transfert de puissance sonore que réalise une onde sonore. On a supposé que les pertes étaient négligeables (hypothèse de linéarité) ; par conséquent, l'onde transmet la puissance acoustique totale de la source émise dans l'angle solide considéré. Au fur et à mesure que l'onde s'éloigne de la source, cette puissance totale se répartit sur une aire croissante.

Quand la distance double, cette surface quadruple. L'intensité acoustique se divise donc par quatre, en champ libre, quand la distance à la source se multiplie par deux. Le niveau d'intensité acoustique diminue de 6 dB (décibels). De ce fait, l'intensité acoustique varie comme l'inverse du carré de la distance à la source sonore considérée :

${\displaystyle {\overrightarrow {I}}({\vec {r}})\propto {\frac {\vec {u}}{r^{2}}}={{\vec {r}} \over r^{3}}}$

Dans ces conditions de champ libre, l'intensité acoustique est proportionnelle au carré de la pression acoustique. Quand la distance à la source se multiplie par deux, la pression se divise par deux (et l'intensité acoustique, proportionnelle au carré de la pression, se divise par quatre, comme nous l'avons indiqué). Le niveau de pression acoustique diminue de 6 dB.

La localisation de l'origine d'un son passe par le flux d'intensité acoustique traversant une surface importante.
Photo Vladimir Granovskiy

Le flux d'intensité acoustique passant à travers une surface orientée importante subit un filtrage directionnel, d'autant plus important que la fréquence est grande. En effet, la puissance transmise à travers un cornet acoustique ou un pavillon acoustique correspond au flux d'énergie sonore passant à travers la surface d'entrée du système :

${\displaystyle \Phi _{S}=\iint _{S}\langle {\vec {I}}_{i}\rangle .{\overrightarrow {\mathrm {d} S}}={\frac {1}{T}}\int _{0}^{T}\left(\iint _{S}p.{\vec {v}}.{\overrightarrow {\mathrm {d} S}}\right).\mathrm {d} t}$

Pour les basses fréquences dont la longueur d'onde est significativement plus grande que l'entrée du système, la valeur du produit ${\displaystyle \scriptstyle p.{\vec {v}}}$ est sensiblement constante sur toute la surface du pavillon à un instant t donné. À ces basses fréquences, l'intégrale est alors simplement :

${\displaystyle \Phi _{S}={\vec {I}}.{\vec {S}}=I.S.\cos(\theta )}$

C'est-à-dire que l'énergie sonore récupérée par le pavillon à basse fréquence dépend simplement de la surface offerte par le pavillon au front d'onde.

Si en revanche on s'intéresse aux fréquences dont la longueur d'onde est significativement plus petite que le diamètre du pavillon, la puissance entrant dans le pavillon à un instant t sera la somme intégrale des intensités acoustiques élémentaires prise sur toute l'étendue de cette surface. La situation est alors très différente suivant que le pavillon est ou non orienté vers la source sonore.

Dans le cas où le vecteur d'intensité acoustique et le vecteur décrivant la surface sont colinéaires, c'est-à-dire si l'ouverture du pavillon est dirigée dans la direction du front d'onde, ${\displaystyle \cos(\theta )=1}$, l'intensité acoustique instantanée sera sensiblement constante sur toute l'étendue du pavillon, et la puissance acceptée par le pavillon sera alors :

${\displaystyle \Phi _{S}=I.S}$

Si au contraire le pavillon fait un angle par rapport au front d'onde, il verra en entrée un mélange de vitesses positives et négatives, d'autant plus déphasées que l'angle ${\displaystyle \theta }$ sera important. L'intégrale de ce signal désynchronisé sera alors pratiquement nulle par rapport au signal reçu de front.

Autrement dit, si l'on trace le diagramme de rayonnement reflétant la transmission de l'énergie pour une fréquence élevée donnée, celui-ci présentera un lobe central important, et des lobes secondaires très rapidement décroissants, la sélectivité angulaire du pavillon étant de l'ordre de la longueur d'onde sonore divisée par le diamètre du pavillon.

Conduit acoustique, transmetteur d'ordres sur un navire (complet avec le bouchon et le sifflet d'appel)

Lorsque les ondes sonores sont guidées par un tuyau rigide, l'énergie sonore injectée à l'une des extrémités du tuyau ne peut pas se disperser, et se retrouve à l'autre extrémité concentrée sur une surface identique.

Ce phénomène est utilisé dans les conduits acoustiques, pour transmettre des ordres à distance (type Chadburn), comme sur un navire dans un environnement bruyant.

C'est également ce phénomène qui est utilisé dans le pavillon acoustique pour transformer l'impédance acoustique entre la haute impédance de la membrane source et la basse impédance de l'air, en conservant constante l'énergie sonore transmise par le cornet.

Par rapport à une source ponctuelle unique, l'intensité acoustique occupe, en mesure acoustique, une fonction assez analogue à celle de l'éclairement en photométrie : c'est l'énergie qui frappe une surface de référence.

Toutefois, en photométrie, cet éclairement peut ensuite être analysé suivant sa distribution angulaire, ce qui définit la luminance. En acoustique, en revanche, l'intensité acoustique se limite à un vecteur unique, dont la direction est définie et ne justifie pas l'étude de sa distribution angulaire.

Il est possible d'analyser dans un deuxième temps la distribution angulaire d'une énergie électromagnétique en un « point » donné, parce que les longueurs d'onde étudiées, de l'ordre du micromètre pour les onde lumineuse, sont d'un ordre de grandeur très inférieur à la taille des éléments de surface considérés (typiquement millimétrique). Il est alors toujours possible de considérer que des photons provenant d'angles solides élémentaires différents sont décorrélés, et d'analyser la distribution d'énergie par rapport à l'angle solide.

Pour une onde sonore, en revanche, les longueurs d'onde étudiées sont généralement d'un ordre de grandeurs très supérieur à la taille des éléments de surface que l'on peut considérer. L'intensité acoustique doit alors s'analyser comme un simple champ vectoriel. Mais inversement, les vitesses des déplacements sonores arrivant sur une surface sont corrélées, et c'est leur interférence dans un flux à travers une surface d'entrée qui peut redonner une information sur la direction d'origine de la source sonore.

Si une paroi crée une perturbation, ou bien à proximité d'une source sonore, la pression et la vitesse ne varient pas ensemble. L'hypothèse de la linéarité permet de décomposer, suivant le théorème de Fourier[8], l'onde sonore en ondes élémentaires, sinusoïdales, dont les effets s'ajouteront par l'application du principe de superposition. Pour chacune de ces ondes élémentaires, on peut appliquer à nouveau le même principe, et les décomposer en une onde où la vitesse et la pression varient ensemble, et une onde où la vitesse et la pression varient en quadrature de phase, c'est-à-dire que lorsque la vitesse est nulle, la pression acoustique est maximale. La première est identique à une onde en champ libre. Pour le cas où la vitesse et la pression sont en quadrature de phase, la moyenne, sur une période complète, est nulle.

L'intensité acoustique représente uniquement les variations de pression et de vitesse en phase. Celles-ci correspondent à un transfert d'énergie dans le sens de propagation. L'autre partie correspond à des ondes stationnaires, dans lesquelles l'énergie transmise dans un sens est égal à celle transmise dans l'autre sens.

La décomposition des ondes sonores en une somme de sinusoïdes de fréquences et de phases différentes permet aussi l'étude de la réponse des systèmes à des signaux, supposés continus, de fréquence variable. On définit ainsi une intensité acoustique complexe, fonction de la fréquence. La partie réelle de cette grandeur complexe est l'intensité acoustique définie précédemment ; la partie imaginaire est la composante réactive, avec la vitesse et la pression en quadrature de phase.

Pour une onde sonore plane, comme on peut en observer dans un tuyau dont le diamètre est inférieur à la demi-longueur d'onde de la vibration sonore, la pression et la vitesse acoustiques varient ensemble. La pression est une force par unité de surface, qui s'exerce sur une masse, celle de l'élément voisin, et lui imprime une accélération, c'est-à-dire une variation de vitesse, selon les lois de la mécanique. La pression et la vitesse acoustiques sont ainsi liées par des équations différentielles, et, dans ces conditions, l'intensité acoustique I se relie à la pression acoustique en un point par la relation :

${\displaystyle I={\frac {p^{2}}{\rho _{0}\cdot c}}\approx {\frac {p^{2}}{400}}.}$

• p est la pression acoustique (Pa), en kg⋅m⁻¹⋅s⁻² ;
• ${\displaystyle \rho _{0}}$ est la masse volumique de l'air, en kg⋅m⁻³ : (1,2 kg m⁻³ aux conditions normales de température, d'humidité et de pression atmosphérique) ;
• c est la vitesse du son, en m⋅s⁻¹ : 340 m/s dans les mêmes conditions [9] ;.

Dans ces conditions, l'intensité (en kg⋅s⁻³) est à peu près égale, à cette condition près, à p²/400 [10].

En champ libre, les ondes ne sont pas planes, mais sphériques, et la pression et la vitesse ne varient pas exactement ensemble. Cependant, plus la sphère grandit, et plus l'onde ressemble à une onde plane. Les calculs avec des ondes sinusoïdales montrent que lorsque la distance à la source est supérieure ou égale à la longueur d'onde, on peut assimiler l'onde sphérique à une onde plane (Rossi 2007, p. 27).

Ces calculs concernent une seule onde sonore progressive. Dans un champ diffus, comme dans le cas du son réverbéré dans un local, le rapport entre pression acoustique et intensité acoustique est entièrement différent. Dans cette situation, une quantité d'ondes allant dans toutes les directions se superposent aux ondes principales. Ces ondes, en s'ajoutant, contribuent à la pression acoustique, mais elles transfèrent l'énergie dans tous les sens, ce qui fait qu'en moyenne, leurs intensité acoustiques instantanées s'annulent. Dans les cas où il existe des ondes stationnaires, ce qui correspond aux situations, en acoustique architecturale, où on trouve des vibrations modales dans une salle, on trouve des pressions acoustiques qui ne correspondent à aucune intensité acoustique.

Si on se représente le milieu qui transmet l'onde sonore comme une suite de ressorts possédant une masse, on peut appliquer à celles-ci les équations de Newton. Selon la seconde équation, l'accélération (c'est-à-dire la variation de vitesse) est égale au quotient de la force par la masse. Dans une portion d'air prise dans une onde sonore, dont la masse est égale à la densité de l'air multipliée par son (très petit) volume, la force appliquée résulte de la différence entre la pression du côté de l'origine de l'onde, multipliée par la surface de la particule de ce côté, et la grandeur homologue du côté opposé.

Avec deux mesures de pression suffisamment proches l'une de l'autre, le quotient de leur différence par la distance entre les deux points de mesure est égal au gradient de pression, dont le quotient par la masse en jeu est égal à l'accélération. On dispose donc d'une mesure de l'accélération. L'accélération étant la dérivée de la vitesse, en procédant à l'intégration de l'accélération, on obtient la vitesse. Pour obtenir l'intensité, il faut encore multiplier celle-ci par la pression, que l'on obtient en effectuant la moyenne entre les deux capteurs.

Résumée ainsi à gros traits, l'opération paraît simple ; les équations qui la déterminent ont été établies au XVIII^e siècle par Euler. La réalisation pratique d'un appareil de mesure, cependant, présente des difficultés, notamment en raison de la nécessité de filtrer les signaux acoustiques pour pouvoir effectuer l'intégration.

Les sondes d'intensité acoustique les plus courantes consistent en deux capteurs de pression disposés face à face, séparés par une entretoise. La distance entre les deux capteurs dépend de la gamme de fréquence qu'il s'agit d'explorer. Ces sondes sont reliées à un appareil qui calcule l'intensité acoustique.

Pour déterminer la direction de l'intensité acoustique, on peut soit rechercher le nul (comme en radiogionométrie), soit rechercher le maximum (ce qui permet d'effectuer la mesure directement) (Brüel & Kjaer 1993, p. 19).

Des normes déterminent l'usage de ces sondes quand il s'agit de calculer la puissance d'émission sonore totale d'un appareil et ses caractéristiques en fonction de la direction.

Avec des capteurs supplémentaires, on peut réaliser des évaluations plus indépendantes de la fréquence[16] ou qui discriminent plus la direction[17].

Avec au moins quatre capteurs dans les trois dimensions, on peut calculer directement la direction dans l'espace de l'intensité acoustique. Avec plus de capteurs, on obtient une reconstruction plus précise du champ sonore. Dans des applications de mesure de bruit, on a des dispositifs encore bien plus spectaculaires, avec des systèmes pouvant atteindre plusieurs dizaines de capteurs[18] dont les résultats sont recoupés par ordinateur.

• Pression acoustique
• Impédance acoustique
• Son
• L’intensité en acoustique musicale
• Acoustique non linéaire

• Patrice Bourcet et Pierre Liénard, « Acoustique fondamentale », dans Le livre des techniques du son, tome 1 - Notions fondamentales, Paris, Eyrolles, 1987
• Antonio Fischetti, Initiation à l'acoustique : Écoles de cinéma — BTS audiovisuel, Paris, Belin, 2001, 287 p.
• Mario Rossi, Audio, Lausanne, Presses Polytechniques et Universitaires Romandes, 2007, 782 p.
• Vincent Martin, Éléments d'acoustique générale : De quelques lieux communs de l'acoustique à une première maîtrise des champs sonores, Lausanne, Presses Polytechniques et Universitaires Romandes, 2007, 411 p.
• (en) Brüel & Kjaer, Sound Intensity : Primer, Nærum, Denmark, Brüel & Kjaer, 1993, 38 p. (lire en ligne) (URI alternative)
• (en) S. Gade, « Sound Intensity (Theory) », Technical Review, Nærum, Denmark, Brüel & Kjaer, n^o 3,‎ 1982, p. 3-43
• (en) S. Gade, « Sound Intensity (Instrumentation and Applications) », Technical Review, Nærum, Denmark, Brüel & Kjaer, n^o 4,‎ 1982, p. 3-32
• (en) Frank J. Fahy, Sound Intensity, London, Spon Press, 1995, 2^e éd. (1^re éd. 1989), 320 p.
• (en) Ray A. Rayburn, Earle's Microphone Book : From Mono to Stereo to Surround — a Guide to Microphone Design and Application, Focal Press, 2012, 3^e éd., 466 p.

• Das Ohmsche Gesetz der Akustik - Schallintensitätsberechnung
• Zusammenhang der akustischen Größen (PDF-Datei; 109 kB)