Icosidodécaèdre
Le solide d'Archimède de vingt faces triangulaires et douze faces pentagonales s’appelle un icosidodécaèdre. Le mot “icosidodécaèdre” commence par “icos”, qui signifie “vingt”, soit le nombre de faces du solide de Platon de douze sommets, qui est le dual du “dodécaèdre” de Platon, dont les douze faces sont pentagonales.

deux à deux à angle droit en leur milieu. L’intersection des solides duaux
est un icosidodécaèdre, dont les arêtes forment six décagones réguliers :
six sections équatoriales communes aux trois solides concentriques.
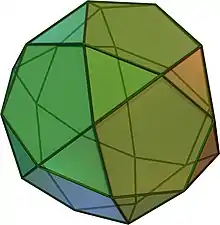
| Faces | Arêtes | Sommets |
|---|---|---|
| 32 : 20 triangles et 12 pentagones | 60 | 30 de degré 4 |
| Type | Solide d'Archimède |
|---|---|
| Caractéristique | 2 |
| Propriétés | quasi régulier et convexe |
| Groupe de symétrie | Ih |
| Dual | Triacontaèdre rhombique |
Description

Cette image‑ci montre l’icosidodécaèdre de face et de dessus, avec deux faces triangulaires horizontales. De dessus le contour est un dodécagone, qui entoure dix triangles et six pentagones. Une moitié des faces est donc visible de dessus : seize faces.
Les soixante arêtes d’un icosidodécaèdre sont les côtés de six décagones réguliers de même taille, convexes et concentriques. Le centre de leurs six cercles circonscrits est le centre de symétrie de chaque décagone, donc le centre de symétrie de l’icosidodécaèdre, centre de sa sphère circonscrite, tangente aux arêtes des deux solides de Platon, dont il est l’intersection. À gauche, chacun des décagones réguliers équatoriaux a sa couleur propre. Les deux projections orthogonales qui se correspondent déforment chaque décagone, alors que dans la toute première image, la première projection de l’icosidodécaèdre respecte la forme du décagone décoré de pois clairs : celui du contour, dans un plan parallèle aux deux faces opposées décorées de pois clairs elles aussi.
Symétriques l’une de l’autre par rapport au centre du solide, deux faces pentagonales opposées ont les mêmes contours bigarrés. Leurs côtés sont parallèles à ceux du décagone, dont la couleur est absente des deux contours. N’importe quelle projection respecte un parallélisme ou une symétrie centrale. Par exemple, dans trois plans parallèles équidistants, deux pentagones opposés et leur décagone parallèle sont trois polygones réguliers, qui se projettent de face sur deux segments bicolores du contour octogonal, et un segment parallèle passant par le centre de la vue.
La vue de dessus ne déforme pas la face supérieure : un triangle équilatéral horizontal, représenté par un segment horizontal dans la vue de face, vue qui respecte la mesure des angles dièdres sur le contour du solide. Par exemple le sommet du contour octogonal, en haut à droite, représente une arête horizontale en bleu terne, commune à un triangle et un pentagone, comme toute autre arête. N’importe quelle arête est celle d’un dièdre partout de même mesure, propriété ainsi énoncée en abrégé : les arêtes sont uniformes. En effet, donner à une autre face triangulaire la même orientation, dans un plan horizontal, aboutirait au tracé du même angle tout en haut du contour octogonal, à droite.
Commun à deux triangles et deux pentagones, chaque sommet est l’extrêmité commune de quatre arêtes, qui forment partout la “même figure”, autrement dit trente figures isométriques. L’icosidodécaèdre est un polyèdre quasi régulier.
Constructions mathématiques
On obtient ce polyèdre entre autres en tronquant un des deux solides de Platon de trente arêtes (l'icosaèdre ou le dodécaèdre) à chaque sommet, par une section qui passe par les milieux de toutes les arêtes issues du sommet tronqué. Ses soixante arêtes égales sont les côtés de six décagones réguliers convexes concentriques : six sections équatoriales du solide tronqué ou du solide initial.
Travail manuel
Un polyèdre montre le nombre et les formes de ses faces par son patron. Ci‑dessus il manque au patron de trente‑deux faces des pattes à encoller, si on veut réellement construire un icosidodécaèdre en papier ou en bristol. En complétant par une section décagonale un demi‑patron d’icosidodécaèdre, on construira une maquette beaucoup moins fragile, très stable quand on la posera sur son décagone. Son pentagone supérieur sera alors horizontal comme son décagone. Remplacer des pattes à encoller, par des pattes à emboîter dans des trous adéquats demande un peu d’expérience. Mais il est bien agréable de pouvoir démonter une maquette, la ranger à plat, et la transporter sans l’abîmer.
L’encastrement des pièces expliqué dans la deuxième image peut entrer dans une progression pédagogique de plusieurs années. Il s’agit de structures démontables de polygones réguliers, imbriqués les uns dans les autres, où les arêtes du polyèdre sont représentées par les bords de trois, ou quatre, ou six pièces imbriquées. La toute première fois on construit ainsi un octaèdre de Platon, plus tard un cuboctaèdre, et un beau jour un icosidodécaèdre. À chaque fois on numérote les pièces par les nombres de leurs paires d’encoches tournées vers l’extérieur. On débute en assemblant trois carrés évidés en 3D, sécants deux à deux selon une diagonale. Plus tard nos quatre hexagones réguliers sont sécants deux à deux selon un diamètre. Dans ces deux premières structures, et enfin dans notre assemblage de six décagones, deux pièces quelconques ont des plans sécants selon un diamètre, commun à leurs deux cercles circonscrits. Et en remplaçant nos pièces polygonales par des couronnes, nous représenterons des sphères dans l’espace.
Nous obtiendrons d’autres polyèdres remarquables, en prolongeant chaque polygone à imbriquer par un autre polygone, séparé du polygone de base par un pli. Le polygone de base, carré, hexagonal ou décagonal, autrement dit la section régulière de base, sera rendue visible grâce à des prolongements évidés. En même temps, les plis auront un intérêt mécanique, ils rigidifient la maquette. Par exemple, nos six pièces décagonales peuvent se prolonger par des triangles isocèles, dont les angles égaux mesurent 36° ou 60°, selon le solide de Platon désiré : dodécaèdre ou icosaèdre. En tronquant de tels prolongements, nous calculerons les pièces d’un solide tronqué, par exemple les six pièces d’un ballon de foot.
Coordonnées et symétries
Un icosidodécaèdre possède une symétrie icosaédrique, et sa première stellation est le composé d'un dodécaèdre et de son dual, l'icosaèdre, avec les sommets de l'icosaèdre localisés aux milieux des arêtes du dodécaèdre.
Avec R rayon de la sphère circonscrit et a longueur de l'arête , on a la relation :
Des coordonnées commodes pour les 30 sommets d'un icosidodécaèdre sont les permutations circulaires de
où est le nombre d'or. En utilisant , on vérifie que ces sommets sont sur une sphère centrée à l'origine.
Polyèdres reliés
Son polyèdre dual est le triacontaèdre rhombique. Un icosidodécaèdre peut être divisé le long de plusieurs plans pour former des rotondes décagonales, qui figurent parmi les solides de Johnson.
Dans la nomenclature standard utilisée pour les solides de Johnson, un icosidodécaèdre serait appelé une gyrobirotonde décagonale . En effet, on obtient un icosidodécaèdre en accolant deux « rotondes » décagonales par leur base, telle que leur face supérieure (les deux pentagones opposés) soient orientées différemment (c'est pourquoi l'on ajoute « gyro- »).
L'icosidodécaèdre est un dodécaèdre tronqué et aussi un icosaèdre tronqué, lorsque les troncatures des sommets du dodécaèdre et de l'icosaèdre sont maximales (rectifications).
Voir aussi
- Cuboctaèdre
- Icosaèdre tronqué
- Grand icosidodécaèdre tronqué
- Petit rhombicosidodécaèdre
- Icosidodécaèdre tronqué (ou « grand rhombicosidodécaèdre »)
Références
, dont la référence était (en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979 (ISBN 978-0-486-23729-9).
Liens externes
- (en) The Uniform Polyhedra sur mathconsult.ch
- (en) Virtual Polyhedra sur le site de George W. Hart (en)






