Histoire de la racine carrée

Schéma de la tablette YBC 7289

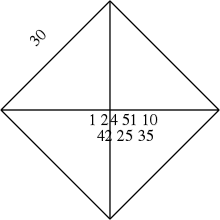
La tablette babylonienne référencée YBC 7289 représente le premier témoignage connu d'une racine carrée[1]. On y reconnait distinctement un carré avec ses diagonales (dont d'autres tablettes confirment la construction). Le dessin est bâclé, avec des écritures que les spécialistes reconnaissent être celle d'un apprenti scribe : c'est un cahier d'exercices.

Les écritures sont des mesures, en particulier sur la diagonale. En système sexagésimal cunéiforme :

1 + 24/60 + 51/60² + 10/60³[2] =~ 1,41421296

Une valeur approchée au six dix-millionièmes de √2 (6 décimales). Des listes d'approximations ont été retrouvées[3] mais aucune tablette n'explique comment ce résultat a été calculé.

Sur plusieurs autres problèmes (diagonale d'un rectangle, côtés de triangles, hexagones et autres polygones) des algorithmes itératifs pour l'extraction de racine carrée proches de la méthode de Héron sont utilisés. Cependant, la stricte application de celle-ci dans une notation sexagésimale ne permet pas de retrouver l'exacte approximation de la tablette YBC 7289. Il faut supposer la réutilisation d'approximations dans la simplification des calculs. De plus, ces processus itératifs sont peu clairs et mélangent les unités, sans qu'il soit évident que le rédacteur ait conscience que les étapes peuvent se répéter à l'infini.

L'exercice des mathématiques pour la majorité des scribes semble consister à recopier et utiliser des résultats établis par d'autres. Toutefois, la précision atteinte dépasse l'utilité pratique, ce qui laisse envisager une utilisation pédagogique.

Nǚwā tenant le compas et son mari Fuxi l’équerre – fouilles archéologiques au Xinjiang

La culture intellectuelle de la Chine classique est généralement littéraire, si bien qu'un grand sinologue osa dire : « L’idée de quantité ne joue autant dire aucun rôle dans les spéculations philosophiques des Chinois. Les Nombres, cependant, intéressent passionnément les Sages de l’ancienne Chine »[5]. Le Dao De Jing (v. -600) donne le ton : « Dào créa l'Un, de l'un poussa le deux, deux fit trois, et du trois naquirent les 10 000 êtres » (42). L'inspiration est poursuivie par le taoïsme (Wang Bi, 226~249), jusqu'au néo-confucianisme (Zhou Dunyi, 1017~1073), notamment en spéculant sur Yi Jing. Au mieux, on lit des dialectiques sur l'un et le multiple[6], mais on y chercherait en vain l'équivalent d'une mystique pythagoricienne de la rationalité. Le théorème de Pythagore et le risque de l'irrationalité ont été vus, quand on constate la faveur des triangles rectangles à côtés commensurables (3,4,5), mais on s'accommode aussi de triplets pythagoriciens approximatifs (4²+8²=9²-1, 4²+7²=8²-1). Le nombre est surtout vidé de la quantité pour en trouver un sens symbolique, propre à étiqueter la diversité du réel. Les examens impériaux pour accéder aux fonctions mandarinales demande une grande connaissance des Classiques chinois, mais ne comportent pas d'épreuves mathématiques.

Cependant, en 1983, on a découvert le plus ancien texte mathématique actuellement connu (-186) dans la tombe d'un lettré fonctionnaire impérial. Le Suàn shù shū 算數書, « écritures de compte », est un ensemble de 190 baguettes traduites très récemment (2004)[7]. Il s'agit d'exemples de calculs, utilisées pour des opérations administratives (« Champs rectangulaires », « Millet et riz », « Taxation équitable », « Excédent et déficit »…)[8].

(-186) Suàn shù shū 算數書, « écritures de compte »
√240 : une approximation acceptable par la méthode de la fausse position

« Mise au carré d'un champ
Soit un champ d'un arpent : de combien de pas est-il carré ? [« arpent » traduit une unité d'aire, mǔ 畝. « pas » traduit une unité de longueur. On sait que 240 步 bù carrés = 1 mǔ 畝. Le problème est donc √240 ?]
Réponse : il est le carré de 15 pas et 15/31 pas [√240=15,491... ; 15+15/31=15,483...].
Méthode : Si c'est un carré de 15, il y a un déficit de 15 [15x15=225=240-15] ; si c'est un carré de 16, il y a un excès de 16 [16x16=256=240+16].
Réponse : Additionner l'excès [16] et le déficit [15] pour faire un diviseur [15+16]. Le numérateur du déficit multiplie le dénominateur de l'excès [15x16], et le numérateur de l'excès multiplie le dénominateur du déficit [16x15] ; additionner pour faire un dividende [(15x16 + 16x15)]. Renverser pour donner la longueur [(15x16 + 16x15)/(15+16)=32x15/31=15+15/31]. »

L'approximation de √240 à laquelle ce texte aboutit est acceptable. Cette première tentative chinoise attestée d'extraction de racine est aussi la première formulation de la méthode de la fausse position (dite Yíng bù zú « excès et déficit ») que l'on retrouve jusqu'à Al-Khwarizmi (783~850). Elle est utilisée ailleurs dans le texte avec exactitude sur des équations linéaires. Ici elle fonctionne comme une approximation. Le calcul peut être difficile à suivre, il prouve en tous cas une grande habitude de manipulation verbale des fractions. Pour nous, en termes fonctionnels, cela consiste à effectuer une moyenne linéaire entre deux valeurs encadrantes. Soit f(x)=x²-240. On cherche x pour que f(x)=0. Par essai et erreur on trouve (1) f(15)=-15 et (2) f(16)=+16, x est entre 15 et 16. Si f était linéaire de type ax+b, elle serait telle que (1) a15+b=-15 et (2) a16+b=16. (2)-(1) ⇒ 16a+b-15a-b=a=16+15=31, d'où a=31. Appliqué à (1) ou (2), on trouve b=-480, d'où l'approximation linéaire f(x)=31x-480=0 ⇒ x=480/31=((31x15)+15)/31=15+15/31, solution initiale du problème. L'algorithme n'est pas appliqué de manière itérative.

Reste une information de contexte qui nous manque, quelle est l'utilité de ce calcul ? Cela semble supposer que le mǔ 畝 est une unité d'aire traditionnelle qui ne s'obtient pas par arpentage, peut-être par évaluation de la production d'une parcelle, ou comme le caractère semble l'indiquer, un temps de travail agricole (久 jiǔ « durée » : 人 rén « un homme » avec un outil ; 田 tián « champ »). Le fonctionnaire qui lisait ce texte a participé à la réforme impériale de Qin Shi Huang (-260~-210). Celle-ci unifia les poids et mesures, appliqua une réforme agraire, afin que des paysans devenus propriétaires produisent les grains nécessaires à des campagnes militaires et des grands travaux. Les nombreux problèmes de conversions devaient donc s'appliquer concrètement dans le calcul des taxes, en confrontation aux unités traditionnelles de la population locale.

Cette approche est très intéressante pour l'histoire des mathématiques et des civilisations en général. Comparé à la tradition grecque, les mathématiques ne sont pas la libre théorie d'une classe oisive[9], elles doivent être utiles à un lettré confucéen qui a une charge envers l'état et le peuple. Il en résulte une moindre clarté d'expression des problèmes, et l'acceptation de solutions pragmatiques, bien éloignées de la perfection religieuse recherchée par exemple dans les veda indiens. Toutefois, cela n'empêche pas une intention de généralisation (plus que d'abstractions), guidée par le paradigme taoïste.

(-200~200) Zhoubi Suanjing 周髀算經, « l'ombre des cycles, livre de calculs »

Écrit astronomique avec des résultats mathématiques, édité et commenté par Liu Hui

Puzzle de Gougu

« Conseils taoïstes d'un mathématicien à son élève (~-100)
« […] tu peux comprendre cette matière si tu lui donnes une pensée sincère et continue […] Pour l'instant, tu ne sais pas généraliser. […] Beaucoup de choses échappent à ta connaissance. La Voie illumine la connaissance quand des mots simples ont une application large. Quand tu interroges un seul problème et y vois une myriade de choses, là, tu entends la Voie. »

— Zhoubi Suanjing, -100~100, in (Cullen 1996, 175-178)

(0~263) JiuZhang SuanShu 九章算術 « Les Neuf Chapitres sur l'art mathématique »
Un classique mathématique édité et commenté par Liu Hui (263)

Le repère suivant est un commentaire de Liu Hui (263), rapportant un texte les Neuf Chapitres sur l'art mathématique[10] datant à peu près de notre ère (un inventaire de la bibliothèque impériale de -5 ne le mentionne pas alors qu'il le sera ensuite). Dans le chapitre 4 少广 Shao guang « la moindre largeur », les questions 12 à 18 impliquent l'extraction de racine carrée selon la méthode de la fausse position du livre précédent. Liu Hui est parfois présenté comme l'Euclide chinois. Qu'il soit chinois est hors de doute, les problèmes et les méthodes n'empruntent rien à d'autres cultures. Par contre, le mode de généralisation n'a rien à voir avec un développement axiomatique. Pour résumer, √2 a été vu, mais pas cherché.

La Grèce connaît et même démontre l'irrationalité de √2, mais cette découverte est difficile à attribuer exactement.

Aristote (-384~-322) tient la démonstration pour acquise et l'utilise comme un exemple d'application du raisonnement par l'absurde et du tiers exclu, il dit juste : « la diagonale du carré est incommensurable à ses côtés, ou cela supposerait que les nombres impairs soient pairs. » (-335~-323)[11], ses auditeurs sont censés connaître la démonstration arithmétique.

√2, pair et impair, démonstration moderne

Si √2 était rationnel, il existerait donc par définition une fraction ou a et b sont entiers et irréductibles, ${\displaystyle {\sqrt {2}}=a/b\Leftrightarrow 2=a^{2}/b^{2}\Leftrightarrow a^{2}=2b^{2}\,}$. Quelle que soit la valeur de b², si a égal 2b², c'est qu'il est multiple de 2, donc pair. Or, si le carré de a est pair, alors a est pair. Ici est la disjonction pointée par Aristote, celle qui exclut une troisième option, le tiers exclus. Un nombre est ou pair ou impair. Si a est impair, ${\displaystyle a=(2x+1)\Rightarrow a^{2}=(2x+1)^{2}=4x^{2}+4x+1=2(2(x^{2}+x))+1=2y+1\,}$, son carré est impair. Si a est pair, ${\displaystyle a=2x\Rightarrow a=2(2x^{2})=2y\,}$, son carré est pair. En conséquence, il existe un entier n, tel que ${\displaystyle a=2n\Rightarrow a^{2}=(2n)^{2}=2(2n^{2})=2b^{2}\Rightarrow b^{2}=2n^{2}\,}$, autrement dit, si a est pair, le carré de b est pair aussi. Comme pour a, si b² est pair, b doit être pair aussi. Là est le nœud du raisonnement, si a et b sont pairs, alors la fraction a/b peut être réduite par 2, ce qui est contradictoire à la définition initiale, donc la définition initiale est fausse, absurde, il n'existe pas de fraction rationnelle irréductible égale à √2. Le même raisonnement se montre pour √3 et les autres racines de nombres premiers .

Platon (-427~-348) évoque un ensemble des racines dans le Théétète. L'action se tient après la mort de Socrate (-399), un tout jeune Euclide (-325~-265) rapporte un dialogue que Socrate aurait eu avec le mathématicien Théétète d'Athènes (-415 ~ -395 ou -369). Le sujet concerne la recherche d'un principe pour définir la science vraie. La définition des irrationnels est utilisée comme un exemple introductif du critère philosophique à chercher. Est aussi cité le mathématicien Théodore de Cyrène (-470~-420), maître de Platon.

L'incompatibilité des dates est évidente. Toutefois, c'est dans le style de Platon d'invoquer dans ses dialogues les figures représentatives d'un problème. Il veut clairement signifier que Théétète hérite de Théodore. Reste qu'Euclide n'était pas né quand Platon mourut. Plusieurs critiques ont voulu supposer un autre Euclide, avec autant de mémoire et de talents. La probabilité est faible. Une autre hypothèse s'accorde tout à fait avec la composition du texte, l'introduction d'Euclide est postérieure, après la mort du maître. On sait qu'avant de rejoindre Alexandrie, le mathématicien naquit à Athènes, et l'Académie restait un centre d'études mathématiques.

Ce court passage montre que les mathématiques d'alors s'appuient toujours sur des analogies géométriques, mais que le discours se poursuit sans recourir à des figures, en énoncés oraux concluants (voir la logique d'Aristote). Certains historiens des sciences parlent même de raisonnement arithmétique précurseur d'une démonstration algébrique. Euclide a donc recueilli une tradition déjà longuement élaborée dans son Livre X des éléments. Il en tire d'autres propositions, en particulier une méthode d'approximation des racines dite d'antiphérèse, ou soustraction réciproque[14]. Les définitions 1 à 3 rappellent celles du Théétète, dans d'autres termes.

Euclide a donc reçu de Théétète la définition d'une classe de nombres incommensurables, ou irrationnels, les racines. Théétète a appris de Théodore la preuve de l'irrationalité des racines jusqu'à 17, probablement par démonstration géométrique. Mais d'où Théodore tient la démonstration pour la première, √2 ? Platon encore, considère la démonstration pour si élémentaire, qu'elle peut être expliquée à un esclave dans le Ménon (duplication du carré). Un néoplatonisme bien postérieur l'attribue à l'école pythagoricienne. Jamblique (250~325) estime qu'elle concerne le partage d'un segment en extrême et moyenne raison, le nombre d'or (1+√5)/2. Pappus d'Alexandrie (340) en parle pour la diagonale du carré (√2), de même Proclos (412~485). Jamblique ajoute une légende très belle, critiquée par Proclos, peut-être le premier (et le dernier ?) martyre mathématique.

Hippase de Métaponte, disciple de Pythagore (v.-580~v.-490), connaissait l'incommensurabilité de √2 (peut-être découverte par son maître). La secte propageait une arithmétique mystique affirmant la rationalité de l'univers au sens mathématique, c’est-à-dire que le sensible est fait de grandeurs pouvant toutes se ramener à l'unité. L'existence d'au moins une seule grandeur irrationnelle prouvée, √2, réfute le principe métaphysique. Hippase aurait enfreint la règle de silence de la communauté, et révélé l'irrationalité du monde. Nous ne connaissons pas les enjeux théologiques de l'époque, mais Hippase a été banni, et se serait même jeté à la mer après avoir perdu l'amitié de ses frères.

Le néo-pythogoricien Théon de Smyrne (70~135), inspiré de la méthode d'antiphérèse d'Euclide, a utilisé le principe de suites encadrantes pour approcher la valeur de √2 (a/b, (a+2b)/(a+b) ... : 3/2, 7/5, 17/12 ...). Enfin Diophante d'Alexandrie (200/214~284/298) aura besoin d'une théorie des nombres unifiant les entiers, les rationnels et les irrationnels, pour la résolution d'une équation diophantienne.

Pour la Grèce antique, √2 est plus qu'un nombre. Ce fut d'abord un problème métaphysique, qui resta une introduction de choix à la philosophie (car « nul n'y entre s'il n'est géomètre »[16]). La question parcourt un millénaire de culture classique, de Pythagore (-580~-490) à Proclos (412~485).

La Civilisation de la vallée de l'Indus (-2600~-1500), contemporaine de la Mésopotamie et l’Égypte ancienne a-t-elle connu √2 ? Son écriture n'a pas encore été déchiffrée, on peut tout au plus s'essayer à des conjectures sur la civilisation matérielle. La présence de briques normalisées (1x2x4) sur le même lieu que des règles précises au millimètre prouve la connaissance pratique de la réduction à l'unité. Ils savent rendre les longueurs commensurables, est-ce que la diagonale du carré leur a posé problème ? Il est dans l'état impossible de déduire les sciences spéculatives du savoir-faire des artisans. Mais la découverte d'un système de poids et mesures d'une grande précision et de caractère décimal, oblige à se demander ce que les mathématiques postérieures doivent à cette culture.

L'époque suivante (-1500~-400) est nommé védique, car elle est essentiellement connue par les Veda, des textes religieux dans une langue indo-européenne, le sanskrit. En appendice, on peut y trouver des Śulba-Sūtras. Ce sont des règles pour construire un autel avec des proportions justes, avec ces mêmes briques de l'Indus, autorisant à se demander si ces textes ne compilent pas des traditions orales bien antérieures. S'il on veut que le sacrifice védique (yajña) plaise aux dieux, il doit être parfait, d'où la motivation à chercher l'exactitude des rapports, comme un temple grec. Les mathématiques ont donc un sens religieux, sans pour autant faire l'objet d'un culte d'un genre pythagoricien, encore moins de démonstrations. L'essentiel est que la règle fonctionne.

Dans son Śulbasutra 52, Baudhayana (-800) explique comment construire un carré d'aire double d'un carré donné, donc de côté √2, en une seule phrase : « qu'on augmente le côté du carré d'un tiers et cela de son quart diminué du trente-quatrième de lui-même ». La figure à construire n'est pas triviale[17], mais la valeur algébrique revient à 1 + 1/3 + 1/4 (1/3 - 1/34 x 1/3) = 1,414215…, précision à 5 décimales. La procédure n'est pas démontrée, il est même difficile de deviner comment elle a été découverte. Un indianiste[18] note que la phrase indienne exacte utilise le mot sanskrit savi´e¸a, signifiant « excède ». Le rédacteur sait que son résultat est supérieur au nombre cherché, et même de combien, l'approximation résulterait d'un processus itératif avec pour étapes :

${\displaystyle {\sqrt {2}}\approx 1+{\dfrac {1}{3}}\approx 1+{\dfrac {1}{3}}+{\dfrac {1}{3}}.{\dfrac {1}{4}}\approx 1+{\dfrac {1}{3}}+{\dfrac {1}{3}}.{\dfrac {1}{4}}-{\dfrac {1}{3}}.{\dfrac {1}{4}}.{\dfrac {1}{34}}\approx 1+{\dfrac {1}{3}}+{\dfrac {1}{3}}.{\dfrac {1}{4}}-{\dfrac {1}{3}}.{\dfrac {1}{4}}.{\dfrac {1}{34}}-{\dfrac {1}{3}}.{\dfrac {1}{4}}.{\dfrac {1}{34}}.{\dfrac {1}{1154}}\ldots }$ (12 décimales de précision).

L'obtention des signes (+/-) et des diviseurs (4, 34, 1154…) repose sur une procédure assez complexe démontrée avec de la géométrie et la proportion des briques ; mais avec finalement très peu de calculs à effectuer. La construction d'autels s'est suffit de 5 décimales de précision.

Il ne faut cependant pas surévaluer la postérité de ces résultats. Ils semblent avoir été abandonnés avec la religion védique. Après la conquête de la Bactriane par Alexandre le Grand (-328), une influence grecque s'est continuée jusqu'au début de notre ère (10) par le royaume indo-grec. Il s'y constitue un syncrétisme gréco-bouddhique évident dans la statuaire, mais les textes conservés ne permettent pas de déterminer si Euclide par exemple a attiré l'attention. Le bouddhisme mahayana diffusé depuis là dans le reste de l'Asie conserve des spéculations astronomiques, mais pas de contribution mathématique notable. Les historiens des sciences préfèrent insister sur le rôle du jaïnisme dans la renouveau classique des mathématiques indiennes, d'ailleurs plus au sud.

Dans le Brahmasphuta-siddhanta « Le système révisé de Brahma » de Brahmagupta (598-668) on trouvera le zéro, une méthode pour calculer les racines carrées et quelques algorithmes pour résoudre des équations du second degré. Ce livre est parvenu aux arabes.

Les mathématiques en langue arabe ont conservé et compris les mathématiques de la Grèce antique, c'est déjà un énorme mérite, elles auraient pu rester lettres mortes, comme les mathématiques babyloniennes. Le nestorien Hunayn ibn Ishaq (809~873)[19] a très tôt traduit les Éléments d'Euclide, relu par le sabéen Thabit ibn Qurra (826~901)[19], qui parlait grec. L'autre apport décisif est d'avoir assimilé les Mathématiques indiennes, en particulier l'écriture décimale positionnelle des nombres à l'aide des chiffres. Toutefois, il faut rappeler que si le perse Al-Khwarizmi (783~850)[19] parle des chiffres indiens dans son algèbre (الجبر و المقابلة - Al-jabr wa’l-muqâbalah ou Abrégé du calcul par la restauration et la comparaison), ses démonstrations restent verbales (Le carré de l'inconnue est nommé «le carré» ou mâl, l'inconnue est «la chose» ou shay ou jidhr, la constante est le dirham ou adǎd. Il appelle les nombres rationnels et irrationnels respectivement 'audibles' et 'inaudibles' (asamm) et la traduction latine a donné pour ces derniers 'surdus' (muet ou sourd). Gérard de Crémone (c. 1150), Fibonacci (1202) et jusqu'à Robert Recorde (1551) utilisent ce terme pour désigner les racines non explicitées.) Al-Khwarizmi a proposé le premier modèle systématique d'algorithmes de résolutions des équations linéaires et quadratiques. √2 est définitivement domestiqué, il n'a plus de mystère.

« René Descartes, Regulae ad directionem ingenii « Les Règles pour la direction de l'esprit », 1628 [Traduit du latin par Georges Le Roy]

[…] nombre de relations [… dont] on cherche à exprimer par plusieurs dimensions et plusieurs figures, et dont on nomme la première racine, la seconde carré, la troisième cube, la quatrième bicarré, etc. Ces termes m'ont moi-même longtemps trompé, je l'avoue; car […] après beaucoup d'expériences je m'aperçus que, par cette manière de concevoir les choses, je n'avais rien découvert que je n'eusse pu connaître bien plus facilement et distinctement sans elle ; et qu'il faut rejeter entièrement de telles dénominations, de peur qu'elles ne troublent la pensée, car, quoiqu'on puisse appeler une grandeur cube ou bicarré, on ne doit jamais la présenter à l'imagination autrement que comme une ligne ou une surface, d'après la règle précédente. Il faut donc noter avant tout que la racine, le carré, le cube, etc. ne sont que des grandeurs en proportion continue. »