Règle des phases

Diagramme de phase de l'eau.
Les courbes représentent les équilibres de deux phases : si la température est fixée, la pression est subie, et réciproquement. Dans les domaines délimités par les courbes une seule phase est stable : on peut y faire varier la pression indépendamment de la température. Le point critique et le point triple ne peuvent être modifiés.

L'eau peut exister dans trois états : solide, liquide, gaz, auxquels on peut adjoindre le fluide supercritique. On a une seule espèce chimique, l'eau, soit ${\displaystyle c=1}$. Le système eau seule n'est le siège d'aucune réaction chimique, soit ${\displaystyle r=0}$. Si l'opérateur n'impose aucune condition opératoire alors ${\displaystyle k=0}$.

Pour l'eau sous forme de solide seul, de liquide seul, de gaz seul ou de fluide supercritique seul, il n'y a qu'une seule phase, soit ${\displaystyle \varphi =1}$ :

${\displaystyle v=1-0-0+2-1=2}$

Il y a donc deux degrés de liberté : à pression donnée la phase étudiée existe seule sur une plage de température plus ou moins étendue. De même, à température donnée la phase étudiée existe seule sur une plage de pression plus ou moins étendue. L'opérateur peut donc imposer la température et la pression indépendamment l'une de l'autre dans le domaine d'existence de la phase étudiée. Si l'opérateur fixe la pression et la température alors ${\displaystyle k=2}$ et ${\displaystyle v=0}$ : le système est entièrement déterminé.

Lors des changements d'état on trouve deux phases en équilibre (solide et liquide, ou liquide et gaz, ou solide et gaz), soit ${\displaystyle \varphi =2}$ :

${\displaystyle v=1-0-0+2-2=1}$

Il n'y a qu'un seul degré de liberté : à température donnée il n'y a qu'une seule pression d'équilibre, et réciproquement. L'opérateur ne peut donc imposer qu'un seul des deux paramètres pour étudier l'équilibre voulu : la température ou la pression, l'autre paramètre est subi. Si l'opérateur fixe la pression ou la température alors ${\displaystyle k=1}$ et ${\displaystyle v=0}$ : le système est entièrement déterminé. Si l'opérateur fixe la pression et la température alors ${\displaystyle k=2}$ et ${\displaystyle v=-1}$ : l'opérateur impose trop de paramètres.

Au point critique il existe toujours une phase gaz et une phase liquide (${\displaystyle \varphi =2}$), mais elles ne se distinguent plus, elles ont les mêmes propriétés physiques, notamment la même masse volumique. Ceci constitue une contrainte supplémentaire (${\displaystyle k=1}$) par rapport à l'équilibre liquide-vapeur existant à des températures et pressions plus basses : la variance réduite est de ${\displaystyle v=0}$. L'opérateur n'a aucune possibilité de modifier les conditions d'apparition du point critique, ce sont des constantes physiques du corps étudié.

Au point triple les trois phases sont en présence, soit ${\displaystyle \varphi =3}$ :

${\displaystyle v=1-0-0+2-3=0}$

Il n'y a aucun degré de liberté au point triple. Comme pour le point critique, l'opérateur ne peut modifier aucune des conditions d'apparition du point triple, ce sont également des constantes physiques du corps étudié.

Un corps pur ne peut être en équilibre sous plus de trois phases simultanément, la variance serait alors négative.

Diagramme binaire isotherme du mélange benzène-toluène obtenu avec la loi de Raoult à température ambiante.
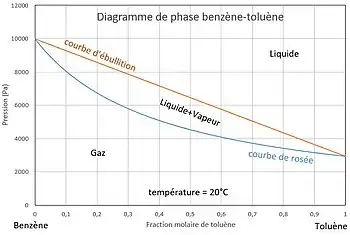
À l'équilibre liquide-vapeur, pour une température donnée, si l'on fixe la composition du liquide, la pression d'équilibre est subie (courbe d'ébullition) ainsi que la composition du gaz (courbe de rosée). Au-dessous de la courbe de rosée le gaz est seul, au-dessus de la courbe d'ébullition le liquide est seul : dans ces domaines on peut fixer, à température donnée, la pression indépendamment de la composition de la phase.

Pour un mélange binaire on a deux constituants, soit ${\displaystyle c=2}$. On suppose qu'il n'est le siège d'aucune réaction chimique, soit ${\displaystyle r=0}$. Si l'opérateur n'impose aucune condition opératoire, alors ${\displaystyle k=0}$.

Pour le mélange sous forme de liquide seul ou de gaz seul, il n'y a qu'une seule phase, soit ${\displaystyle \varphi =1}$ :

${\displaystyle v=2-0-0+2-1=3}$

Il y a trois degrés de liberté. L'opérateur peut donc imposer la température, la pression et la concentration d'un composant indépendamment l'une de l'autre dans le domaine d'existence de la phase étudiée.

Lors des changements d'état on trouve deux phases en équilibre (liquide et gaz), soit ${\displaystyle \varphi =2}$ :

${\displaystyle v=2-0-0+2-2=2}$

Il y a deux degrés de liberté. Si l'opérateur fixe la température et la concentration de l'un des composants dans l'une des phases, la pression et la composition de l'autre phase sont subies. L'opérateur ne peut donc imposer à la fois la température, la pression et la composition de l'une des phases : avec ${\displaystyle k=3}$ on a ${\displaystyle v=-1}$.

Un azéotrope présente une contrainte supplémentaire par rapport au cas précédent : les deux phases ont la même composition. La variance est donc diminuée d'un degré de liberté (${\displaystyle k=1}$) ; la variance réduite vaut :

${\displaystyle v=1}$

Si l'opérateur veut obtenir une composition particulière de l'azéotrope, afin de favoriser l'un des deux produits, il n'a pas le choix de la pression et de la température.

Diagramme de phase semi-logarithmique pression-température de l'eau. Les chiffres romains correspondent aux diverses phases de glace.

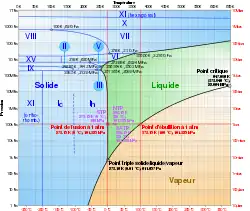
Un corps à l'état solide peut présenter diverses formes cristallines ou moléculaires : il s'agit de l'allotropie pour les corps simples et plus généralement du polymorphisme. Chacune des formes solides doit être comptée comme une phase ${\displaystyle \varphi }$ à part entière dans la règle des phases.

Le diagramme ci-contre montre les domaines d'existence des différentes formes de la glace d'eau en fonction de la pression et de la température. Il existe un point triple à 100 K et 62 GPa. On compte :

• ${\displaystyle c=1}$ pour l'eau pure ;
• ${\displaystyle r=0}$ en l'absence de réaction ;
• ${\displaystyle k=0}$ en l'absence de contrainte ;
• ${\displaystyle n=2}$ pour la température et la pression ;
• ${\displaystyle \varphi =3}$ (phases VII, VIII et X) ;

la variance vaut :

${\displaystyle v=1-0-0+2-3=0}$

Il existe d'autres points triples impliquant trois solides. Le long de la courbe d'équilibre liquide-solide se trouvent plusieurs points triples impliquant deux phases solides et l'eau liquide. Comme pour le point triple solide-liquide-gaz, l'opérateur ne peut modifier les conditions de pression et température de tous ces points triples.

La combustion du soufre solide S en présence d'oxygène O₂ forme du dioxyde de soufre SO₂ et du trioxyde de soufre SO₃ en phase gaz selon deux réactions :

${\displaystyle {\rm {S(s)+O_{2}(g)\rightleftarrows SO_{2}(g)}}}$

${\displaystyle {\rm {S(s)+{3 \over 2}\,O_{2}(g)\rightleftarrows SO_{3}(g)}}}$

L'équilibre entre les deux oxydes n'est pas indépendant puisqu'il est une combinaison des deux réactions précédentes :

${\displaystyle {\rm {SO_{2}(g)\rightleftarrows S(s)+O_{2}(g)}}}$

${\displaystyle {\underline {\rm {S(s)+{3 \over 2}\,O_{2}(g)\rightleftarrows SO_{3}(g)}}}}$

${\displaystyle {\rm {SO_{2}(g)+{1 \over 2}\,O_{2}(g)\rightleftarrows SO_{3}(g)}}}$

On a quatre constituants (${\displaystyle c=4}$ : S, SO₂, SO₃ et O₂), deux réactions (${\displaystyle r=2}$) et deux phases (${\displaystyle \varphi =2}$ : solide et gaz). Si l'opérateur n'impose aucune condition opératoire, alors ${\displaystyle k=0}$. La variance vaut :

${\displaystyle v=4-2-0+2-2=2}$

L'opérateur peut imposer la pression d'oxygène et la température indépendamment l'une de l'autre selon le rendement cherché en l'un des deux produits SO₂ et SO₃.

Dans le procédé Haber-Bosch, l'ammoniac NH₃ est synthétisé en phase gaz à partir d'azote N₂ et d'hydrogène H₂ selon la réaction :

${\displaystyle {\rm {N_{2}(g)+3\,H_{2}(g)\rightleftarrows 2\,NH_{3}(g)}}}$

On a ${\displaystyle c=3}$ (NH₃, N₂ et H₂), ${\displaystyle r=1}$, ${\displaystyle k=0}$, ${\displaystyle n=2}$ et ${\displaystyle \varphi =1}$ (gaz), d'où la variance :

${\displaystyle v=3-1-0+2-1=3}$

L'opérateur peut fixer la pression, la température et la composition en azote ou en hydrogène selon le rendement en ammoniac cherché.

Par contre si l'on part de l'ammoniac pur, celui-ci se décompose selon la réaction inverse :

${\displaystyle {\rm {2\,NH_{3}(g)\rightleftarrows N_{2}(g)+3\,H_{2}(g)}}}$

Il y a une contrainte supplémentaire par rapport au cas précédent : le mélange à l'équilibre contient trois fois plus d'hydrogène que d'azote. La variance est donc diminuée d'un degré de liberté ; la variance réduite vaut :

${\displaystyle v=2}$

L'opérateur peut fixer la pression et la température indépendamment l'une de l'autre, la composition est alors subie. Il peut également se fixer la composition finale en ammoniac, de façon à éviter au maximum sa décomposition, et ajuster en conséquence la température (ou la pression) en subissant la pression (respectivement la température).

De façon générale, si les réactifs d'une réaction chimique sont introduits à la stœchiométrie, les produits seront également formés à la stœchiométrie. Ceci constitue donc une contrainte supplémentaire à inclure dans ${\displaystyle k}$, puisque l'opérateur impose une condition opératoire.

Diagramme de solubilité du chlorure de sodium dans l'eau.
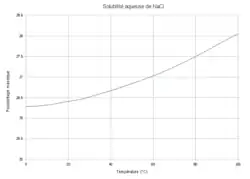
Sur la courbe, à saturation, si l'opérateur fixe une température la solubilité est subie, et réciproquement. Sous la courbe, en sous-saturation, l'opérateur peut imposer la température indépendamment de la concentration en sel dans la solution.

Le chlorure de sodium NaCl solide se dissout dans l'eau sous forme de deux ions : l'ion sodium Na⁺ et l'ion chlorure Cl⁻. La réaction s'écrit :

${\displaystyle {\rm {NaCl(s)\rightleftarrows Na^{+}(aq)+Cl^{-}(aq)}}}$

À l'équilibre réactionnel (état de saturation, la concentration en sel dissout est alors appelée solubilité du sel) on a :

• quatre constituants, soit ${\displaystyle c=4}$ (l'eau, NaCl, Na⁺ et Cl⁻) ;
• une réaction, soit ${\displaystyle r=1}$ ;
• une contrainte supplémentaire avec l'électroneutralité de la solution liquide qui impose que le nombre de charges positives (cations Na⁺) soit le même que celui de charges négatives (anions Cl⁻) ; on a donc, si l'opérateur ne fixe aucun paramètre, ${\displaystyle k=1}$ ;
• la présence de phases condensées uniquement (solide et liquide, pas de gaz), la pression n'a donc qu'une influence négligeable sur l'équilibre, on compte ${\displaystyle n=1}$ pour la température seule ;
• deux phases (un liquide et un solide, NaCl), soit ${\displaystyle \varphi =2}$.

La variance réduite vaut :

${\displaystyle v=4-1-1+1-2=1}$

Il n'y a donc qu'un seul degré de liberté. Si l'opérateur fixe la température, la solubilité du sel est subie ; réciproquement, pour obtenir une certaine solubilité l'opérateur n'a pas le choix de la température.

En revanche, si la quantité de sel dissout est insuffisante pour atteindre la solubilité, la solution n'est pas saturée et le sel solide n'est pas présent : cet état est qualifié de sous-saturation. On a alors trois constituants (${\displaystyle c=3}$ : l'eau, Na⁺ et Cl⁻), pas de réaction (${\displaystyle r=0}$), l'électroneutralité (${\displaystyle k=1}$) et une seule phase (${\displaystyle \varphi =1}$ : le liquide) ; la variance réduite vaut :

${\displaystyle v=3-0-1+1-1=2}$

En état de sous-saturation l'opérateur peut fixer indépendamment la température et la concentration en sel dissout, qui est alors inférieure à la solubilité à la même température. Cet état est un état d'équilibre, différent de l'équilibre à saturation car la phase solide n'existe pas, et la réaction n'a pas lieu.

Le passage de l'état de sous-saturation à celui de saturation, et inversement, est une rupture d'équilibre. Si l'on part de l'état de sous-saturation, donc en l'absence de NaCl solide, il y a déplacement d'équilibre lorsque l'on refroidit, ou lorsque l'on extrait de l'eau, tant que le sel reste entièrement dissout. Lorsque le sel précipité apparait la solution passe en état de saturation, il y a rupture d'équilibre : un nouvel état physico-chimique apparait en présence d'une nouvelle phase (solide), d'un nouveau constituant (NaCl) et d'une nouvelle réaction chimique (la précipitation). Inversement, si l'on part de l'état de saturation, donc en présence de NaCl solide, il y a déplacement d'équilibre lorsque l'on augmente la température, ou lorsque l'on ajoute de l'eau, tant que la phase solide subsiste : du sel se dissout progressivement. Lorsque le sel solide disparait la solution passe en état de sous-saturation, il y a rupture d'équilibre : un nouvel état physico-chimique apparait en l'absence de la phase solide, du constituant NaCl et de la réaction de précipitation.

On dissout simultanément au NaCl du sulfate de sodium Na₂SO₄, qui produit des ions sulfate SO^2-
₄ selon la réaction :

${\displaystyle {\rm {Na_{2}SO_{4}(s)\rightleftarrows 2\,Na^{+}(aq)+SO_{4}^{2-}(aq)}}}$

L'ion Na⁺ est commun aux deux sels NaCl et Na₂SO₄. Avec :

• ${\displaystyle c=6}$ (l'eau, NaCl, Na₂SO₄, Na⁺, Cl⁻ et SO^2-
  ₄) ;
• ${\displaystyle r=2}$ ;
• ${\displaystyle k=1}$ pour l'électroneutralité (le nombre de cations Na⁺ est égal à celui d'anions Cl⁻ plus deux fois celui de SO^2-
  ₄) ;
• ${\displaystyle n=1}$ ;
• ${\displaystyle \varphi =3}$ (un liquide et deux solides, NaCl et Na₂SO₄) ;

la variance réduite vaut :

${\displaystyle v=6-2-1+1-3=1}$

Si l'opérateur fixe la température les solubilités des deux sels sont subies. Si l'opérateur fixe la solubilité de l'un des sels, la solubilité de l'autre sel et la température sont subies.

Si le Na₂SO₄ est introduit en quantité insuffisante pour atteindre la saturation, il est entièrement dissout : il ne compte pas parmi les composants (${\displaystyle c=5}$ pour l'eau, NaCl, Na⁺, Cl⁻ et SO^2-
₄), le seul équilibre est celui du NaCl (${\displaystyle r=1}$), l'électroneutralité est toujours vraie (${\displaystyle k=1}$) ainsi que ${\displaystyle n=1}$, et le seul solide est NaCl en présence du liquide (${\displaystyle \varphi =2}$). La variance réduite vaut :

${\displaystyle v=5-1-1+1-2=2}$

L'opérateur peut fixer indépendamment la température et la concentration en SO^2-
₄ ou Cl⁻. En effet, si l'opérateur ajoute du Na₂SO₄, l'ajout conséquent de Na⁺ fait précipiter le NaCl. Il peut ainsi contrôler la concentration de Cl⁻ dans la solution.

On obtient ${\displaystyle v=3}$ si NaCl est également introduit en quantité insuffisante pour atteindre la saturation. L'opérateur peut fixer indépendamment la température et les concentrations en Cl⁻ et SO^2-
₄.

Au lieu de Na₂SO₄ on dissout en même temps que le NaCl du sulfate d'argent Ag₂SO₄, qui réagit selon :

${\displaystyle {\rm {Ag_{2}SO_{4}(s)\rightleftarrows 2\,Ag^{+}(aq)+SO_{4}^{2-}(aq)}}}$

Les deux sels NaCl et Ag₂SO₄ ne forment pas d'ion commun. Avec :

• ${\displaystyle c=7}$ (l'eau, NaCl, Ag₂SO₄, Na⁺, Ag⁺, Cl⁻ et SO^2-
  ₄) ;
• ${\displaystyle r=2}$ ;
• ${\displaystyle k=2}$ ; on a trois contraintes supplémentaires dont deux seulement sont indépendantes :
  • le nombre d'ions Na⁺ égale celui de Cl⁻ ;
  • le nombre d'ions Ag⁺ est le double de celui de SO^2-
    ₄ ;
  • l'électroneutralité est composée des deux contraintes précédentes (le nombre de cations Na⁺ plus celui de Ag⁺ est égal au nombre d'anions Cl⁻ plus deux fois celui de SO^2-
    ₄) ;
• ${\displaystyle n=1}$ ;
• ${\displaystyle \varphi =3}$ (un liquide et deux solides, NaCl et Ag₂SO₄) ;

la variance réduite vaut :

${\displaystyle v=7-2-2+1-3=1}$

Comme pour le cas avec ion commun, si l'opérateur fixe la température les solubilités des deux sels sont subies. Si l'opérateur fixe la solubilité de l'un des sels, la solubilité de l'autre sel et la température sont subies.

On obtient ${\displaystyle v=2}$ si Ag₂SO₄ est introduit en quantité insuffisante pour atteindre la saturation. La variance est identique au cas avec ion commun, cependant ici l'ajout de Ag₂SO₄ n'a aucune influence sur la quantité de NaCl dissout car les deux réactions sont indépendantes. L'opérateur ne peut modifier indépendamment que la température et la teneur en Ag₂SO₄ dissout, la quantité de NaCl dissout est subie.

Si le NaCl est également en sous-saturation, on a ${\displaystyle v=3}$. Les conclusions sont identiques à celles du cas avec ion commun : on peut faire varier indépendamment la température et les deux concentrations des sels dissouts.

Livres

• Jean-Claude Legrand, L'indispensable en Thermodynamique chimique : les applications, Bréal, 2003 (ISBN 978-2-7495-2241-8, lire en ligne), p. 15-17.
• J. Mesplède, Chimie : Thermodynamique Matériaux PC, Bréal (ISBN 978-2-7495-2064-3, lire en ligne), p. 86-90.
• Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique : + de 6500 termes, nombreuses références historiques, des milliers de références bibliographiques, Louvain-la-Neuve, De Boeck supérieur, 2018, 976 p. (ISBN 978-2-8073-0744-5, lire en ligne), p. 559.
• Michel Soustelle, Équilibres chimiques, vol. 4, Londres, ISTE Group, coll. « Génie des procédés / Thermodynamique chimique approfondie », 2015, 196 p. (ISBN 978-1-78405-103-7, lire en ligne), p. 82-85 ; p. 93.

Article

• Mohamed Jemal, « Sur le calcul de la variance », L'actualité de la chimie, n^o 333,‎ août-septembre 2009, p. 38-41 (lire en ligne [PDF], consulté le 1^er mai 2020).

• « Variance d'un système en équilibre », sur sciences-en-ligne.com (consulté le 1^er mai 2020).