Polynôme de Tutte

Soit ${\displaystyle G=(V,E)}$ un graphe non orienté, avec ensemble de sommets ${\displaystyle V}$ et ensemble d'arêtes ${\displaystyle E}$. Pour ${\displaystyle A\subseteq E}$, on note ${\displaystyle (V,A)}$ le graphe partiel qui a les mêmes sommets que ${\displaystyle G}$, et ses arêtes dans ${\displaystyle A}$.

Definition.- Le polynôme de Tutte d'un graphe ${\displaystyle G=(V,E)}$ est le polynôme ${\displaystyle T_{G}(x,y)}$ défini par :

${\displaystyle T_{G}(x,y)=\sum \nolimits _{A\subseteq E}(x-1)^{k(A)-k(E)}(y-1)^{k(A)+|A|-|V|}}$,

où ${\displaystyle k(A)}$ est le nombre de composantes connexes du graphe ${\displaystyle (V,A)}$. L'exposant ${\displaystyle k(A)+|A|-|V|}$ du deuxième facteur est le nombre cyclomatique de ${\displaystyle (V,A)}$.

On peut donner une formulation légèrement différente de la même définition en posant

${\displaystyle r(A)=|V|-k(A)}$,

où ${\displaystyle r(A)}$ est le rang de Whitney du graphe ${\displaystyle (V,A)}$. La fonction génératrice des rangs de Whitney est définie par :

${\displaystyle R_{G}(u,v)=\sum \nolimits _{A\subseteq E}u^{r(E)-r(A)}v^{|A|-r(A)}}$.

Les deux fonctions sont équivalentes par un simple changement de variables. On a en effet :

${\displaystyle T_{G}(x,y)=R_{G}(x-1,y-1)}$.

Le polynôme dichromatique ${\displaystyle Q_{G}}$ de Tutte résulte d'une autre transformation simple. On a :

${\displaystyle T_{G}(x,y)=(x-1)^{-k(G)}Q_{G}(x-1,y-1)}$.

Définition originale.- La définition originale de ${\displaystyle T_{G}}$ de Tutte est équivalente, mais moins facile à formuler. Pour un graphe connexe ${\displaystyle G}$, on a

${\displaystyle T_{G}(x,y)=\sum \nolimits _{i,j}t_{ij}x^{i}y^{j},}$

où ${\displaystyle t_{ij}}$ est le nombre d'arbres couvrants d'« activité interne » ${\displaystyle i}$ et d' « activité interne » ${\displaystyle j}$[5].

Contraction-suppression.- Une troisième définition est par récurrence sur la suppression d'arêtes. La contraction d'arête ${\displaystyle uv}$ d'un graphe ${\displaystyle G}$ produit le graphe ${\displaystyle G/uv}$ obtenu en fusionnant les sommets ${\displaystyle u}$ et ${\displaystyle v}$ et en supprimant l'arête ${\displaystyle uv}$. On note ${\displaystyle G-uv}$ le graphe où l'on a seulement supprimé l'arête ${\displaystyle uv}$, sans fusionner ses deux extrémités. Le polynôme de Tutte est défini par récurrence par

${\displaystyle T_{G}(x,y)={\begin{cases}xT_{G/e}(x,y)&{\text{si }}\ e\ {\text{ est un isthme}},\\yT_{G-e}(x,y)&{\text{si }}\ e\ {\text{ est une boucle}},\\T_{G-e}(x,y)+T_{G/e}(x,y)&{\text{sinon}}.\end{cases}}}$

selon que ${\displaystyle e}$ est boucle un isthme, ou ni l'un ni l'autre, avec la condition initiale

${\displaystyle T_{G}=1}$ si ${\displaystyle G}$ ne contient pas d'arête.

Le « random cluster model » de la mécanique statistique dû à Fortuin et Kasteleyn 1972 fournit encore une autre définition équivalente[6] : Le polynôme

${\displaystyle Z_{G}(q,w)=\sum \nolimits _{F\subseteq E}q^{k(F)}w^{|F|}}$

est lié à ${\displaystyle T_{G}}$ par la transformation [7] :

${\displaystyle T_{G}(x,y)=(x-1)^{-k(E)}(y-1)^{-|V|}\cdot Z_{G}{\Big (}(x-1)(y-1),\;y-1{\Big )}.}$

Le polynôme de Tutte se factorise pour les composantes connexes : Si ${\displaystyle G}$ est l'union disjointe de graphes ${\displaystyle H}$ et ${\displaystyle H'}$, alors

${\displaystyle T_{G}=T_{H}\cdot T_{H'}}$.

Si ${\displaystyle G}$ est un graphe planaire et si ${\displaystyle G^{*}}$ dénote son graphe dual, alors

${\displaystyle T_{G}(x,y)=T_{G^{*}}(y,x)}$.

En particulier, le polynôme chromatique d'un graphe planaire est le polynôme de flot de son dual.

Deux graphes isomorphes ont même polynôme de Tutte, mais la réciproque est fausse. Par exemple, le polynôme de Tutte de tout arbre ayant ${\displaystyle m}$ arêtes est ${\displaystyle x^{m}}$.

Un polynôme de Tutte peut être donné sous forme de table, en présentant dans un tableau le coefficient ${\displaystyle t_{ij}}$ de ${\displaystyle x^{i}y^{j}}$ en ligne ${\displaystyle i}$ et colonne ${\displaystyle j}$. Par exemple, le polynôme de Tutte du graphe de Petersen, qui est :

${\displaystyle {\begin{aligned}36x&+120x^{2}+180x^{3}+170x^{4}+114x^{5}+56x^{6}+21x^{7}+6x^{8}+x^{9}\\&+36y+84y^{2}+75y^{3}+35y^{4}+9y^{5}+y^{6}\\&+168xy+240x^{2}y+170x^{3}y+70x^{4}y+12x^{5}y\\&+171xy^{2}+105x^{2}y^{2}+30x^{3}y^{2}\\&+65xy^{3}+15x^{2}y^{3}\\&+10xy^{4},\end{aligned}}}$

est donné par la table suivante :

0	36	84	75	35	9	1
36	168	171	65	10
120	240	105	15
180	170	30
170	70
114	12
56
21
6
1

Un autre exemple, est le polynôme de Tutte du graphe octaédrique et :

${\displaystyle {\begin{aligned}&12\,{y}^{2}{x}^{2}+11\,x+11\,y+40\,{y}^{3}+32\,{y}^{2}+46\,yx+24\,x{y}^{3}+52\,x{y}^{2}\\&+25\,{x}^{2}+29\,{y}^{4}+15\,{y}^{5}+5\,{y}^{6}+6\,{y}^{4}x\\&+39\,y{x}^{2}+20\,{x}^{3}+{y}^{7}+8\,y{x}^{3}+7\,{x}^{4}+{x}^{5}\end{aligned}}}$

Le polynôme chromatique dans le plan de Tutte.

Pour ${\displaystyle y=0}$, le polynôme de Tutte se spécialises en le polynôme chromatique :

${\displaystyle \chi _{G}(\lambda )=(-1)^{|V|-k(G)}\lambda ^{k(G)}T_{G}(1-\lambda ,0),}$

où ${\displaystyle k(G)}$ est le nombre de composantes connexes de ${\displaystyle G}$.

Pour des valeurs entières de ${\displaystyle \lambda }$, la valeur du polynôme chromatique ${\displaystyle \chi _{G}(\lambda )}$ est égale au nombre de colorations du graphe ${\displaystyle G}$ en utilisant ${\displaystyle \lambda }$ couleurs. Clairement ${\displaystyle \chi _{G}(\lambda )}$ ne dépend pas de l’ensemble de couleurs. Ce qui est moins clair, c'est que c'est la valeur en ${\displaystyle \lambda }$ d'un polynôme à coefficients entiers. Pour voir cela, on observe que :

1. si G a n sommets et pas d'arêtes, alors ${\displaystyle \chi _{G}(\lambda )=\lambda ^{n}}$.
2. si G contient une boucle, alors ${\displaystyle \chi _{G}(\lambda )=0}$.
3. si e est une arête qui n'est pas une boucle, alors

${\displaystyle \chi _{G}(\lambda )=\chi _{G\setminus e}(\lambda )-\chi _{G/e}(\lambda ).}$

Ces trois conditions permettent de calculer ${\displaystyle \chi _{G}(\lambda )}$ en appliquant une suite de contractions-suppressions, mais elles ne garantissent pas que des séquences différentes de suppressions et contractions conduisent au même résultat ; ceci provient du fait que ${\displaystyle \chi _{G}(\lambda )}$ compte des propriétés combinatoires, indépendamment de la récurrence. En particulier,

${\displaystyle T_{G}(2,0)=(-1)^{|V|}\chi _{G}(-1)}$

donne le nombre d'orientations acycliques du graphe.

Polynômes de Jones dans le plan de Tutte.

Sur l'hyperbole ${\displaystyle xy=1}$, le polynôme de Tutte d'un graphe planaire se spécialise en le polynôme de Jones d'un nœud alternant associé.

${\displaystyle T_{G}(2,1)}$ compte le nombre de forêts, c'est-à-dire le nombre des sous-ensembles d'arêtes sans cycle.

${\displaystyle T_{G}(1,1)}$ compte le nombre de forêts couvrantes (c'est le nombre d'ensembles d'arêtes sans cycle et qui ont même nombre de composants connexes que G). Si le graphe est connexe, ${\displaystyle T_{G}(1,1)}$ compte le nombre d'arbres couvrants.

${\displaystyle T_{G}(1,2)}$ compte le nombre de sous-graphes couvrants (ensemble d'arêtes qui ont même nombre de composantes connexes que G).

${\displaystyle T_{G}(2,0)}$ compte le nombre d'orientations acycliques (en) de G[12] - [13].

${\displaystyle T_{G}(0,2)}$ compte le nombre d'orientations fortement connexes de G[14].

Si G est un graphe 4-régulier, alors

${\displaystyle (-1)^{|V|+k(G)}T_{G}(0,-2)}$

compte le nombre d'orientations eulériennes de G. Ici, ${\displaystyle k(G)}$ est le nombre de composantes connexes de G[12].

Si G est un graphe grille de paramètres ${\displaystyle m\times n}$, alors ${\displaystyle 2T_{G}(3,3)}$ compte le nombre de manière de paver un rectangle de largeur 4m et de hauteur 4n avec des tétrominos[15] - [16].

Si G est un graphe planaire, alors ${\displaystyle 2T_{G}(3,3)}$ est égal à la somme des partitions eulériennes pondérées du graphe médial de G, où le poids d'une orientation est 2 à la puissance le nombre de points selle de cette orientation (c'est-à-dire le nombre de sommets où l'orientation des arêtes incidentes est cycliquement « in, out, in out »)[17].

Les fonctions de partition pour le modèle d'Ising et pour les modèles de Potts à 3 et 4 états, dans le plan de Tutte..

On considère l'hyperbole ${\displaystyle H_{2}}$ définie par :

${\displaystyle H_{2}:\quad (x-1)(y-1)=2}$.

Sur cette hyperbole, le polynôme de Tutte se spécialise en la fonction de partition ${\displaystyle Z(\cdot ),}$ du modèle d'Ising étudiée en physique statistique. Plus précisément, le long de l'hyperbole ${\displaystyle H_{2}}$ ces deux fonctions sont liées par l'équation[18] :

${\displaystyle Z(G)=2\left(e^{-\alpha }\right)^{|E|-r(E)}\left(4\sinh \alpha \right)^{r(E)}T_{G}\left(\coth \alpha ,e^{2\alpha }\right).}$

Le lien avec l'hyperbole vient de ce que

${\displaystyle (\coth \alpha -1)\left(e^{2\alpha }-1\right)=2}$

pour tout nombre complexe ${\displaystyle \alpha }$.

Plus généralement, si on définit, pour tout entier q, l'hyperbole :

${\displaystyle H_{q}:\quad (x-1)(y-1)=q}$,

le polynôme de Tutte se spécialise en la fonction de partition du modèle de Potts (en) à q états. Diverses quantités physiques analysées dans le contexte du modèle de Potts se transposent en des parties spécifiques de ${\displaystyle H_{q}}$.

Correspondances entre le modèle de Potts et le plan de Tutte[19]

modèle de Potts	polynôme de Tutte
Ferromagnétisme	Branche positive de ${\displaystyle H_{q}}$
Antiferromagnétisme	Branche négative de ${\displaystyle H_{q}}$ avec ${\displaystyle y>0}$
Haute température	Asymptote de ${\displaystyle H_{q}}$ pour ${\displaystyle y=1}$
Basse temperature ferromagnétique	Branche positive de ${\displaystyle H_{q}}$ asymptotique en ${\displaystyle x=1}$
Température nulle antiferromagnetique	q-coloration du graphe, c'est-à-dire ${\displaystyle x=1-q,y=0}$.

Le polynôme de flot dans le plan de Tutte.

Au point ${\displaystyle x=0}$, le polynôme de Tutte se spécialise en un polynôme appelé polynôme de flot et étudié en combinatoire. Pour un graphe non orienté connexe G et un entier k, un k-flot qui ne s'annule pas (« nowhere-zero flow ») est une affectations de valeurs de « flot » ${\displaystyle 1,2,\dots ,k-1}$ aux arcs d'une orientation arbitraire de G telle que le flot total entrant et le flot total sortant de chaque sommet sont égaux modulo k. Le polynôme de flot ${\displaystyle C_{G}(k)}$ compte le nombre de ces k-flots. Cette valeur est étroitement liée au polynôme chromatique : en fait, si G est un graphe planaire, le polynôme chromatique de G est équivalent au polynôme de flot de son graphe dual ${\displaystyle G^{*}}$ par le théorème de Tutte suivant :

${\displaystyle C_{G}(k)=k^{-1}\chi _{G^{*}}(k)}$.

La connexion avec le polynôme de Tutte est donnée par :

${\displaystyle C_{G}(k)=(-1)^{|E|+|V|+k(G)}T_{G}(0,1-k)}$.

Le polynôme de fiabilité dans le plan de Tutte.

Pour ${\displaystyle x=1}$, le polynôme de Tutte se spécialise en le polynôme de fiabilité entre tous points étudié en théorie des réseaux. Pour un graphe connexe G, on affecte une probabilité p à la suppression d'une arête, pour modéliser un réseau sujet à des pannes aléatoires d'arêtes. Le polynôme de fiabilité est le polynôme ${\displaystyle R_{G}(p)}$ en p qui donne la probabilité qu'un couple de sommets de G reste connecté après des pannes sur les arêtes. Le lien avec le polynôme de Tutte est donné par :

${\displaystyle R_{G}(p)=(1-p)^{|V|-k(G)}p^{|E|-|V|+k(G)}T_{G}(1,1/p)}$.

Tutte a aussi défini une généralisation en deux variables des polynômes chromatiques voisine de ces derniers ; il les appelle polynômes dichromatiques. Pour un graphe ${\displaystyle G=(V,E)}$, c'est le polynôme

${\displaystyle Q_{G}(u,v)=\sum \nolimits _{A\subseteq E}u^{k(A)}v^{|A|-|V|+k(A)},}$

où ${\displaystyle k(A)}$ est le nombre de composantes connexes du graphe partiel ${\displaystyle (V,A)}$. Ce polynôme est relié au « corank-nullity polynomial » par

${\displaystyle Q_{G}(u,v)=u^{k(G)}\,R_{G}(u,v).}$

Le polynôme dichromatique ne se généralise pas au matroïdes parce ${\displaystyle k(A)}$ n'est pas une propriété de matroïdes : des graphes avec même matroïde peuvent avoir un nombre différent de composantes connexes.

Le polynôme de Martin ${\displaystyle m_{\vec {G}}(x)}$ d'un graphe orienté 4-régulier ${\displaystyle {\vec {G}}}$ a été défini par Pierre Martin in 1977[20]. Il a prouvé que si ${\displaystyle G}$ est un graphe planaire et si ${\displaystyle {\vec {G}}_{m}}$ est son graphe médial orienté, alors

${\displaystyle T_{G}(x,x)=m_{{\vec {G}}_{m}}(x).}$

L'algorithme de suppression–contraction applique au graphe diamant. Les arêtes rouges sont supprimées dans l'enfant gauche, contractées dans l'enfant droit. Le polynôme résultant est la somme des monômes des feuilles, ${\displaystyle x^{3}+2x^{2}+y^{2}+2xy+x+y}$. Basé sur (Welsh et Merino 2000).

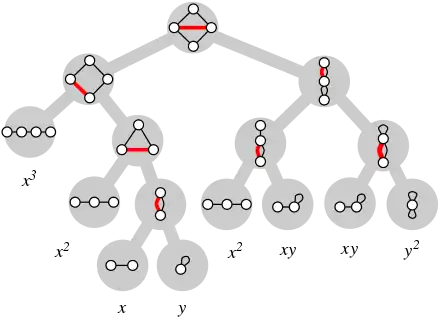
La formule de récurrence de suppression–contraction pour le polynôme de Tutte s'écrit :

${\displaystyle T_{G}(x,y)=T_{G-e}(x,y)+T_{G/e}(x,y)}$,

lorsque ${\displaystyle e}$ n'est ni une boucle ni un isthme. Ceci donne immédiatement un algorithme récursif pour le calcul du polynôme : choisir une arête quelconque e et appliquer la formule jusqu'à ce que toutes les arêtes restantes sont soit des boucles, soit des isthmes. Les cas restants sont alors faciles à évaluer.

À un facteur polynomial près, le temps de calcul t de cet algorithme peut être exprimé en fonction du nombre n de sommets et du nombre m d'arêtes du graphe,

${\displaystyle t(n+m)=t(n+m-1)+t(n+m-2)}$ ;

cette relation est similaire à celle des nombres de Fibonacci avec pour solution[21] :

${\displaystyle t(n+m)=\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n+m}=O(1.6180^{n+m}).}$

L'analyse peut être améliorée par un facteur polynomial en le nombre ${\displaystyle \tau (G)}$ d'arbre couvrants du graphe donné[22]. Pour des graphes creux, avec ${\displaystyle m=O(n)}$ ce temps de calcul est en ${\displaystyle O(\exp(n))}$. Pour les graphes réguliers de degré k, le nombre d'arbres couvrants peut être borné par

${\displaystyle \tau (G)=O\left(\nu _{k}^{n}n^{-1}\log n\right),}$ avec ${\displaystyle \nu _{k}={\frac {(k-1)^{k-1}}{(k^{2}-2k)^{k/2-1}}}}$,

de sorte que l'algorithme de suppression–contraction s'exécute avec un facteur polynomial de cette borne. On a par exemple[23] : ${\displaystyle \nu _{5}\approx 4.4066.}$

En pratique, un test d'isomorphisme de graphes est utilisé pour éviter des appels récursifs. Cette approche fonctionne bien pour des graphes que sont creux et qui présentent beaucoup de symétries ; l'efficacité dépend alors de l'heuristique utilisé pour choisir l'arête e[22] - [24] - [25]. Le choix de l'arête à supprimer s'avère primordial[26].

Dans certains cas particuliers, le polynôme de Tutte peut être calculé en temps polynomial parce que l'élimination de Gauss-Jordan permet un calcul efficace des opérations matricielles comme le déterminant et le pfaffien. Ces algorithmes constituent eux-mêmes des résultats importants en théorie algébrique des graphes et en mécanique statistique .

${\displaystyle T_{G}(1,1)}$ est égal au nombre ${\displaystyle \tau (G)}$ d'arbres couvrants d'un graphe connexe. Cette valeur peut se calculer en temps polynomial en tant que déterminant de la sous-matrice principale maximale de la matrice laplacienne de G, un résultat ancien de la théorie algébrique des graphes connu sous le nom de théorème de Kirchhoff. De façon similaire, la dimension de l'espace à deux cycles de ${\displaystyle T_{G}(-1,-1)}$ peut être calculé par élimination de Gauss en temps polynomial.

Pour les graphes planaires, la fonction de partition du modèle d'Ising, c'est-à-dire le polynôme de Tutte sur l'hyperbole ${\displaystyle H_{2}}$, peut être exprimée comme un pfaffian et calculé de façon efficace au moyen de l'algorithme FKT. Cette idée a été développée par Fisher, Kasteleyn et Temperley pour calculer le nombre de pavages par des dominos pour paver un modèle en treillis plan.

En utilisant une méthode de Monte-Carlo par chaînes de Markov, le polynôme de Tutte peut être approximé d'arbitrairement près sur la branche positive de ${\displaystyle H_{2}}$, qui est aussi la fonction de partition du modèle d'Ising ferromagnétique. Elle exploite le lien étroit entre le modèle d'Ising et le problème du comptage des couplages dans un graphe. L'idée derrière ce célèbre résultat de Jerrum et Sinclair[27] est de définir une chaîne de Markov dont les états sont les couplages du graphe donné. Les transitions sont définies en choisissant aléatoirement des arêtes et en modifiant le couplage en conséquence. La chaîne de Markov obtenue est rapidement mélangeante et conduit à des couplages « suffisamment aléatoires » qui peuvent être utilisées pour récupérer la fonction de partition par un échantillonnage aléatoire. L'algorithme obtenu est un schéma d'approximation en temps polynomial (FPRAS).

Le plan de Tutte. À chaque point ${\displaystyle (x,y)}$ du plan réel est associée la complexité du calcul de ${\displaystyle T_{G}(x,y)}$ :
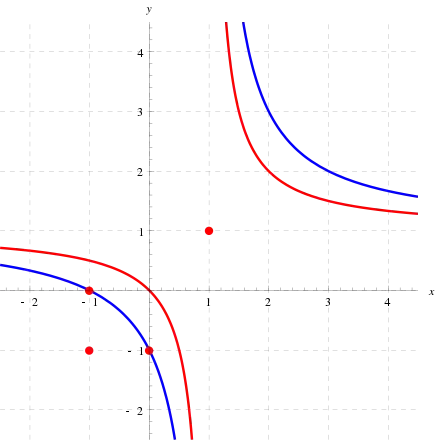
● en un point rouge, le calcul est en temps polynomial ;
● sur une courbe bleue, le problème est #P-difficile en général, mais polynomial pour les graphes planaires ;
● pour tout point des régions blanches, le problème est #P-difficile même pour les graphes planaires bipartis.

Si x et y sont tous deux des entiers positifs ou nuls, le problème du calcul de ${\displaystyle T_{G}(x,y)}$ est dans la classe #P. Pour des entiers relatifs, le polynôme de Tutte contient des termes négatifs, ce qui place le problème dans la classe de complexité GapP (en), qui est la fermeture par soustraction de la classe #P. Pour prendre en compte des coordonnées ${\displaystyle (x,y)}$ rationnelles, on peut définir une classe correspondant à #P[28].

La complexité algorithmique du calcul exact de ${\displaystyle T_{G}(x,y)}$ se partage en deux classes selon la valeur de ${\displaystyle x,y\in \mathbb {C} }$. Le problème est #P-difficile sauf si ${\displaystyle (x,y)}$ est un point de l'hyperbole ${\displaystyle H_{1}}$ ou est l’un des points de l'ensemble suivant (avec ${\displaystyle j=e^{2i\pi /3}}$) :

${\displaystyle \{(1,1),(-1,-1),(0,-1),(-1,0),(i,-i),(-i,i),(j,j^{2}),(j^{2},j)\}}$,

auquel cas le calcul est en temps polynomial[29]. Pour les graphes planaires, le problème devient polynomial aussi pour les points sur l'hyperbole ${\displaystyle H_{2}}$, mais reste #P-difficile pour les autres points, même pour les graphes planaires bipartis[30]. Dans la conclusion de son article sur la dichotomie pour les graphes planaires[31], Vertigan note que le même résultat reste valable même pour la restriction supplémentaire aux graphes de degré au plus trois, à l'exception du point ${\displaystyle T_{G}(0,-2)}$, qui compte les flots « nowhere-zero » ${\displaystyle Z_{3}}$ pour lequel le polynôme se calcul en temps polynomial.

Ces résultats admettent divers cas particuliers intéressants. Par exemple, le problème du calcul de la fonction de partition du modèle d'Ising est #P-difficile en général, même avec l'algorithme d'Onsager et Fisher de résolution dans les treillis planaires. De même, les polynômes de Jones sont #P-difficiles à évaluer. Enfin, le calcul du nombre de 4-coloriages d'un graphe planaire est #P-complet, alors que le problème de décision est trivial par le théorème des quatre couleurs. En revanche, compter le nombre de 3-coloriages d'un graphe planaire est #P-complet parce que le problème de décision est connu pour être NP-complet.

Les points qui possèdent un bon algorithme d'approximation sont peu connus. En dehors des points pour lequel le calcul exact peut être fait en temps polynomial, le seul algorithme d'approximation connu pour ${\displaystyle T_{G}(x,y)}$ est l'algorithme FPRAS de Jerrum et Sinclair, qui est valable pour les points sur l'hyperbole d'Ising ${\displaystyle H_{2}}$ pour y > 0. Si le graphe donné est restreint aux instances denses, avec degré ${\displaystyle \Omega (n)}$, alors il existe un FPRAS pour x ≥ 1, y ≥ 1[32]. Même si les résultats sont moins complets que pour le calcul exact, on sait que de larges portions du plan sont difficiles à approximer[28].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Tutte polynomial » (voir la liste des auteurs).

Livres et monographies

Articles

• polynôme de Bollobás–Riordan (en)

• (en) « Tutte polynomial », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)
• (en) Eric W. Weisstein, « Tutte polynomial », sur MathWorld
• (en) « Chromatic polynomial », sur PlanetMath.