Graphe médial
En théorie des graphes, le graphe médial du graphe planaire G est un graphe M(G) qui représente les adjacences entre les côtés des faces de G. Les graphes médiaux ont été introduits en 1922 par Ernst Steinitz dans l'étude des propriétés combinatoires des polyèdres convexes[1], bien que la construction inverse ait déjà été utilisée par Peter Tait en 1877, dans son étude fondamentale des nœuds et entrelacs [2] - [3] - [4].
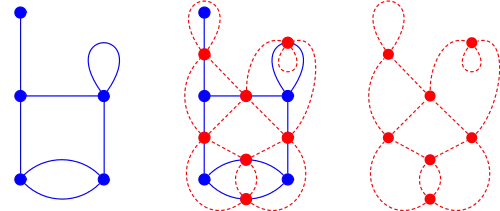
La définition formelle
Étant donné un graphe planaire G, son graphe médial M(G) est le graphe dont les sommets sont les arêtes de G, deux sommets étant reliés si les arêtes de G correspondantes sont consécutives dans une de ses faces. Le graphe médial est donc un sous-graphe du line graph L(G).
La notion de graphe médial s'étend aux graphes plongés dans des surfaces de genre quelconque.
Propriétés
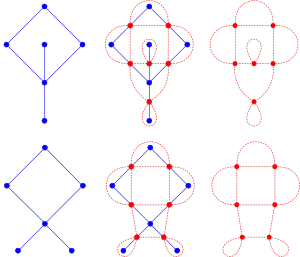
- Le graphe médial d'un graphe planaire est lui aussi planaire, et de plus ses sommets sont d'ordre 4 (il est 4-régulier).
- Le graphe médial de G et celui de son dual sont isomorphes. Inversement, pour tout graphe planaire 4-régulier H, il existe exactement deux graphes planaires ayant H pour graphe médial et ces deux graphes sont duaux l'un de l'autre[5].
- Comme le graphe médial est associé à un plongement particulier du graphe G, deux plongements différents peuvent donner naissance à des graphes médiaux non isomorphes. Dans la représentation ci-contre, les deux graphes médiaux rouges ne sont pas isomorphes car les deux sommets à boucles sont reliés par une arête dans l'un, et pas dans l'autre.
- Pour obtenir l'un des deux graphes G dont H est le médial, colorier les faces de H avec deux couleurs, ce qui est possible puisque H est eulérien (et donc le graphe dual de H est biparti). Les sommets de G correspondent aux faces d'une couleur donnée. Ces sommets sont reliés par une arête si les faces correspondantes ont un sommet en commun dans H. Notons que l'exécution de cette construction à l'aide des faces de l'autre couleur que la couleur choisie produit le graphe dual de G.
Applications
Pour un graphe planaire G, le double de la valeur du polynôme de Tutte au point (3,3) est égal à la somme des orientations eulériennes pondérées dans le graphe médial de G, où le poids d'une orientation est entre 2 et le nombre de sommets de l'orientation (c'est-à-dire le nombre de sommets dont les arêtes incidentes sont cycliquement ordonnées «in, out, in out»)[6]. Puisque le polynôme de Tutte est invariant par plongement, ce résultat montre que chaque graphe médial a la même somme des orientations eulériennes pondérées.
Graphe médial orienté
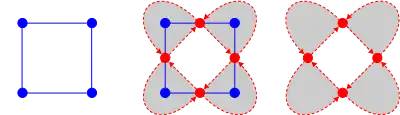
La définition du graphe médial peut être étendue de sorte à inclure une orientation. Tout d'abord, on colorie les faces du graphe médial en noir si elles contiennent un sommet du graphe originel et en blanc sinon. Cette coloration fait que chaque arête du graphe médial est bordée par une face noire et une face blanche. Ensuite, chaque arête est orientée de telle sorte que la face noire soit sur sa gauche.
Un graphe planaire et son dual n'ont pas le même graphe médial orienté ; ils sont transposés l'un de l'autre.
En utilisant le graphe médial orienté, on peut généraliser le résultat sur l'évaluation du polynôme de Tutte en (3,3). Pour un graphe planaire G , la valeur du polynôme de Tutte au point ( n + 1, n + 1) multipliée par n donne la somme pondérée sur toutes les colorations d'arêtes en utilisant n couleurs dans le graphe médial orienté de G, de sorte que chaque ensemble (éventuellement vide) d'arêtes monochromatiques forme un graphe orienté eulérien, où le poids d'une orientation d'Euler est entre 2 et le nombre de sommets monochromatiques[7].
Voir aussi
Références
- Ernst Steinitz, « Polyeder und Raumeinteilungen », Enzyklopädie der mathematischen Wissenschaften, vol. 3 (Geometries), , p. 1–139.
- Peter Guthrie Tait, « On Knots », Proceedings of the Royal Society of Edinburgh, vol. 9, , p. 306–317 (DOI 10.1017/S0370164600032338).
- Peter Guthrie Tait, « On Links », Proceedings of the Royal Society of Edinburgh, vol. 9, , p. 321–332 (DOI 10.1017/S0370164600032363).
- Peter Guthrie Tait, « Additional Remarks on Knots », Proceedings of the Royal Society of Edinburgh, vol. 9, , p. 405 (DOI 10.1017/S0370164600032703).
- Jonathan L. Gross et Jay Yellen (éditeurs), Handbook of Graph Theory, CRC Press, (ISBN 978-1-58488-090-5, lire en ligne), p. 724.
- Michel Las Vergnas, « On the evaluation at (3, 3) of the Tutte polynomial of a graph », Journal of Combinatorial Theory, Series B, vol. 45, no 3, , p. 367-372 (DOI 10.1016/0095-8956(88)90079-2, lire en ligne).
- Joanna A. Ellis-Monaghan, « Identities for circuit partition polynomials, with applications to the Tutte polynomial », Advances in Applied Mathematics, vol. 32, nos 1-2, , p. 188-197 (DOI 10.1016/S0196-8858(03)00079-4, lire en ligne).