Théorème de Kirchhoff
Dans le domaine de la théorie des graphes, le théorème de Kirchhoff, aussi appelé matrix-tree theorem, nommé d'après le physicien Gustav Kirchhoff, est un théorème donnant le nombre exact d'arbres couvrants pour un graphe non orienté quelconque. C'est une généralisation de la formule de Cayley qui donne ce résultat pour les graphes complets non orientés.
Énoncé
Le théorème de Kirchhoff s'appuie sur la notion de matrice laplacienne, définie elle-même comme la différence entre la matrice des degrés et la matrice d'adjacence du graphe. Formellement, pour un graphe où , la matrice laplacienne est définie par :
Le théorème de Kirchhoff s'énonce ainsi :
Théorème — Le nombre d'arbres couvrants du graphe est égal, au signe près, à la valeur de n'importe quel cofacteur de .
Exemple
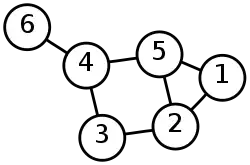
Calcul de la matrice laplacienne
On calcule d'abord la matrice laplacienne de ce graphe :
- Le sommet 1 est de degré 2 et il est relié aux sommets 2 et 5 : la première colonne vaut (2, -1, 0, 0, -1, 0).
- Le sommet 2 est de degré 3 et il est relié aux sommets 1, 3 et 5 : la deuxième colonne vaut (-1, 3, -1, 0, -1, 0).
- Le sommet 3 est de degré 2 et il est relié aux sommets 2 et 4 : la troisième colonne vaut (0, -1, 2, -1, 0, 0).
- Le sommet 4 est de degré 3 et il est relié aux sommets 3, 5 et 6 : la quatrième colonne vaut (0, 0, -1, 3, -1, -1).
- Le sommet 5 est de degré 3 et il est relié aux sommets 1, 2 et 4 : la cinquième colonne vaut (-1, -1, 0, -1, 3, 0).
- Le sommet 6 est de degré 1 et il est relié au sommet 4 : la sixième colonne vaut (0, 0, 0, -1, 0, 1).
Cela donne la matrice laplacienne :
Calcul d'un des cofacteurs
On supprime ensuite n'importe quelle ligne et n'importe quelle colonne de la matrice. Si l'on supprime par exemple la troisième colonne et la deuxième ligne :
Le cofacteur est . D'après le théorème de Kirchhoff, il y a 11 arbres couvrants.
Vérification
Le graphe possède en effet 11 arbres couvrants, ce que l'on peut effectivement constater dans la figure suivante :

Cas des graphes non connexes
Si le graphe de départ n'est pas connexe, alors la matrice laplacienne sera diagonale par bloc. En supprimant une ligne et une colonne, il y aura au moins une composante connexe pour laquelle aucune colonne n'aura été supprimée. La somme des colonnes de cette composante est alors nulle, donc tout cofacteur est nul. On retrouve bien le fait que seuls les graphes connexes ont des arbres couvrants.
Démonstration
Étape 1
Soit une orientation quelconque de , et la matrice d'incidence associée: si a nœuds et arêtes, alors est une matrice à lignes et colonnes dont le terme général est défini par:
Calculons le terme général de : il correspond au produit scalaire de deux lignes de .
- Si , alors si une arête relie à , indépendamment de la direction, et sinon.
- Si , alors compte pour des arêtes sortant de et pour des arêtes arrivant à , donc .
Finalement, on a : .
Étape 2
On ne considère que les graphes connexes, ce qui assure . On considère alors une sous-matrice carrée de .
Le sous-graphe correspondant à contient donc nœuds et arêtes, donc soit c'est un arbre couvrant, soit il contient un cycle. S'il contient un cycle, alors la somme des colonnes correspondantes dans sera nulle, et donc le déterminant de sera nul lui aussi.
S'il ne contient pas de cycle, c'est un arbre couvrant , qui contient au moins deux feuilles. a donc au moins une ligne correspondant à une feuille, donc une ligne contenant termes nuls et un terme égal à ou . En développant le déterminant de par rapport à cette ligne, on obtient donc une relation de récurrence sur le nombre de nœuds du graphe. Si le graphe a un seul nœud, est la matrice vide de déterminant par convention, donc quelle que soit la valeur de , si représente un arbre couvrant , .
En résumé, soit le sous-graphe contient un cycle et dans ce cas , soit le sous-graphe représente un arbre couvrant et dans ce cas .
Étape 3
Soit obtenue en supprimant une ligne quelconque de . Le déterminant de est donc un cofacteur de , au signe près. Par la formule de Binet-Cauchy, on obtient :
où représente les sous-matrices de . D'après l'étape 2, les termes de la somme valent 1 pour chaque arbre couvrant, et 0 sinon, ce qui termine la démonstration.
Applications
La formule de Cayley
Le théorème de Kirchhoff permet de donner une démonstration rapide de la formule de Cayley. Cette dernière indique que le graphe complet possède arbres couvrants.
Génération aléatoire et algorithmique
Le théorème de Kirchoff est utilisé pour générer des arbres couvrants de façon probabiliste. Certains algorithmes probabilistes utilisent ensuite ces arbres[1].
Histoire
Le théorème de Kirchoff est l'une des premières applications de la matrice laplacienne d'un graphe[1]. Cet objet est maintenant très utilisé, notamment en théorie spectrale des graphes.
Notes et références
- (en) Shayan Oveis Gharan, « Recent Advances in Approximation Algorithms : Random Spanning Trees », sur Université de Washington, .
Voir aussi
Bibliographie
(en) John M. Harris, Jeffry L. Hirst et Michael J. Mossinghoff, Combinatorics and Graph Theory, New York, Springer, coll. « Undergraduate Texts in Mathematics », , 2e éd., 381 p. (ISBN 978-0-387-79711-3, lire en ligne), p. 47-50





















































