Algorithme FKT
L'algorithme FKT, nommé ainsi d'après Michael Fisher, Pieter Kasteleyn (en) et Harold N. Temperley, compte le nombre de couplages parfaits dans un graphe planaire, et ceci en temps polynomial. Le même dénombrement est #P-complet pour les graphes généraux. Pour les couplages qui ne sont pas nécessairement parfaits, leur dénombrement reste #P-complet même pour les graphes planaires. L'idée clé de l'algorithme FKT est de convertir le problème en le calcul du pfaffien d'une matrice antisymétrique obtenue à partir d'un plongement planaire du graphe. Le pfaffien de cette matrice est ensuite calculé efficacement à l'aide d'algorithmes standards pour les déterminants .
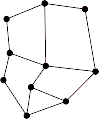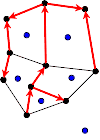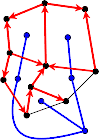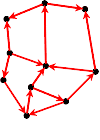
Origines
Le problème du dénombrement des couplages parfaits planaires a ses racines dans la mécanique statistique et la chimie, où la question initiale est la suivante : si des molécules diatomiques sont adsorbées par une surface en formant une seule couche, de combien de manières peuvent-elles être agencées[1]? La fonction de partition, qui code les propriétés statistiques d'un système à l'équilibre, peut être utilisée pour répondre à cette question. Cependant, tenter de calculer la fonction de partition à partir de sa définition n'est pas facile. Aussi, pour résoudre exactement un système physique, il faut trouver une autre formulation de la fonction de partition pour ce système physique particulier qui est suffisamment simple pour être calculée exactement[2]. Au début des années 1960, la définition du terme « exactement soluble » n'était pas précise[3]. L'informatique a fourni une définition rigoureuse avec l'introduction du temps polynomial, qui date de 1965. De même, la notion de « exactement soluble » correspond à #P-dur, notion qui a été définie en 1979.
Un autre type de système physique concerné est composé de dimères, des polymères à deux atomes. Le modèle dimère compte le nombre de revêtements dimères d'un graphe[4]. Un autre système physique est la liaison des molécules d'eau sous forme de glace. Il peut être modélisé comme un graphe 3-régulier orienté où l'orientation des arêtes à chaque sommet peut ne pas être la même. La question posée est le nombre d'orientations d'arêtes dans ce modèle ?
Motivés par des systèmes physiques impliquant des dimères, en 1961, Kasteleyn[5] d'une part, et Temperley et Fisher[6] d'autre part ont indépendamment déterminé le nombre de pavages de dominos du rectangle de taille m x n. Cela équivaut à compter le nombre de couplages parfaits pour le graphe grille m par n. En 1967, Kasteleyn a généralisé ce résultat à tous les graphes planaires[7].
Algorithme
Explication
L'idée principale est que chaque terme non nul dans le pfaffien de la matrice d'adjacence d'un graphe G correspond à un couplage parfait. Ainsi, si l'on peut trouver une orientation de G pour aligner tous les signes des termes dans le pfaffien (soit à + soit à - ), alors la valeur absolue du pfaffien est exactement le nombre de couplages parfaits dans G. L'algorithme FKT effectue une telle tâche pour un graphe planaire G. L'orientation qu'il trouve s'appelle une orientation pfaffienne.
Soit G = ( V, E ) un graphe non orienté, et soit A sa matrice d'adjacence. On définit PM ( n ) comme étant l'ensemble des partitions de n éléments en paires. Le nombre de couplages parfaits dans G est donné par :
Le lien avec pfaffien d'une -matrice A est le suivant :
où sgn( M ) est la signature de la permutation M. Une orientation pfaffienne de G est un graphe orienté H avec une matrice d'adjacence B à coefficients (1, 0, -1) telle que pf( B ) = CP( G )[8]. En 1967, Kasteleyn a prouvé que les graphes planaires ont une orientation pfaffienne calculable efficacement. Plus précisément, pour un graphe planaire G, soit H une version orientée de G où un nombre impair d'arêtes sont orientés dans le sens des aiguilles d'une montre pour chaque face dans un plongement planaire de G . Alors H est une orientation Pfaffienne de G .
Enfin, pour toute matrice antisymétrique A ,
- ,
où det( A ) est le déterminant de A. Ce résultat est dû à Arthur Cayley[9]. Puisque les déterminants sont calculables efficacement, il en est de même de CP( G ).
Description de l'algorithme
- Calculer un plongement planaire de G .
- Calculer un arbre couvrant T1 du graphe d'entrée G .
- Orienter de façon arbitraire chaque arête de G qui est dans T1 .
- Utiliser le plongement planaire pour créer un graphe (non orienté) T2 avec le même ensemble de sommets que le graphe dual de G .
- Créer une arête dans T2 entre deux sommets si leurs faces correspondantes dans G partagent une arête dans G qui n'est pas dans T1. (On observe que T2 est un arbre. )
- Pour chaque feuille v dans T2 qui n'est pas la racine faire :
- Soit e l'arête isolée de G dans la face qui correspond à v et qui n'a pas encore d'orientation.
- Donner à e une orientation telle que le nombre d'arêtes orientées dans le sens des aiguilles d'une montre soit impair.
- Supprimer v de T2 .
- Retourner la valeur absolue du pfaffien de la matrice d'adjacence sur (-1,0,1) de G qui est la racine carrée du déterminant.
Généralisations
La somme des couplages parfaits pondérés peut également être calculée en utilisant la matrice de Tutte à la place de la matrice d'adjacence à la dernière étape.
Le théorème de Kuratowski dit qu'un graphe fini est planaire si et seulement s'il ne contient pas de sous-graphe homéomorphe à K5 (le graphe complet sur cinq sommets) ou K3,3 (le graphe biparti complet sur deux ensembles de taille trois). Vijay Vazirani a généralisé l'algorithme FKT aux graphes qui ne contiennent pas de sous-graphe homéomorphe à K3,3[10]. Étant donné que compter le nombre de couplages parfaits dans un graphe général est #P-complet, une certaine restriction sur le graphe d'entrée est nécessaire à moins que la classe de complexité FP, la version de fonction de la classe P, soit égale à #P . Le dénombrement des couplages, dont le nombre est connu sous le nom d'indice de Hosoya, est également #P-complet, même pour les graphes planaires[11].
Applications
L'algorithme FKT a été largement utilisé dans les algorithmes holographiques sur des graphes planaires via des matchgates[3]. Par exemple, en considérant la version planaire du modèle de glace mentionné ci-dessus, qui porte le nom technique de « #PL-3-NAE » (où NAE signifie "not all equal"), Valiant a trouvé un algorithme en temps polynomial pour ce problème qui utilise des matchgates[12].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « FKT algorithme » (voir la liste des auteurs).
- Brian Hayes, « Accidental Algorithms », American Scientist, january–february 2008 (lire en ligne).
- Rodney J. Baxter, Exactly Solved Models in Statistical Mechanics, Dover Publications, (1re éd. 1982) (ISBN 978-0-486-46271-4, lire en ligne), p. 11.
- Jin-Yi Cai, Pinyan Lu et Mingji Xia « Holographic Algorithms with Matchgates Capture Precisely Tractable Planar #CSP » () (arXiv 1008.0683)
—51st Annual IEEE Symposium on Foundations of Computer Science (FOCS) 2010 (lire en ligne). - Richard Kenyon et Andrei Okounkov, « What is a Dimer? », AMS, vol. 52, no 3, , p. 342–343 (lire en ligne).
- Pieter Kasteleyn, « The statistics of dimers on a lattice. I. The number of dimer arrangements on a quadratic lattice », Physica, vol. 27, no 12, , p. 1209–1225 (DOI 10.1016/0031-8914(61)90063-5)
- H. N. V. Temperley et Michael E. Fisher, « Dimer problem in statistical mechanics-an exact result », Philosophical Magazine, vol. 6, no 68, , p. 1061–1063 (DOI 10.1080/14786436108243366).
- Pieter Kasteleyn, « Dimer Statistics and Phase Transitions », Journal of Mathematical Physics, vol. 4, no 2, , p. 287–293 (DOI 10.1063/1.1703953).
-
Robin Thomas « A survey of Pfaffian orientations of graphs » () (lire en ligne)
—International Congress of Mathematicians (lire en ligne). - Arthur Cayley, « Sur les determinants gauches », Crelle's Journal, vol. 38, , p. 93–96.
- Vijay V. Vazirani, « NC algorithms for computing the number of perfect matchings in K3,3-free graphs and related problems », Information and Computation, vol. 80, no 2, , p. 152–164 (ISSN 0890-5401, DOI 10.1016/0890-5401(89)90017-5).
- Mark Jerrum, « Two-dimensional monomer-dimer systems are computationally intractable », Journal of Statistical Physics, vol. 48, no 1, , p. 121–134 (DOI 10.1007/BF01010403, Bibcode 1987JSP....48..121J).
- Leslie G. Valiant « Holographic Algorithms (Extended Abstract) » () (DOI 10.1109/FOCS.2004.34)
—FOCS'04 (lire en ligne)
— « (ibid.) », dans Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, Rome, Italy, IEEE Computer Society (ISBN 0-7695-2228-9), p. 306–315.
Lien externe
- D'autres informations et exemples peuvent être trouvés dans le chapitre 2 et la section 5.3.2 de la thèse de doctorat de Dmitry Kamenetsky
- Yann Strozecki, « Comptage des couplages parfaits dans un graphe planaire », (consulté le ) (même fichier aussi Comptage des couplages parfaits dans un graphe planaire sur studylibfr.com.



