Fonction polylogarithme
La fonction polylogarithme (aussi connue sous le nom de fonction de Jonquière) est une fonction spéciale qui peut être définie pour tout s et |z| < 1 par :
Le paramètre s et l'argument z sont pris sur l'ensemble ℂ des nombres complexes. Les cas particuliers s = 2 et s = 3 sont appelés le polylogarithme d'ordre 2 ou dilogarithme et le polylogarithme d'ordre 3 ou trilogarithme respectivement. Le polylogarithme apparaît aussi dans la forme fermée de l'intégrale de la distribution de Fermi-Dirac et la distribution de Bose-Einstein et est quelquefois connue comme l'intégrale de Fermi-Dirac ou l'intégrale de Bose-Einstein.
Par prolongement analytique, on peut également donner un sens au polylogarithme pour |z| ≥ 1.
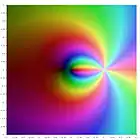 |
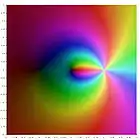 |
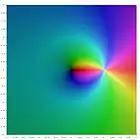 |
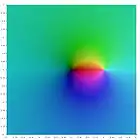 |
 |
 |
 |
| Li-3(z) | Li-2(z) | Li-1(z) | Li0(z) | Li1(z) | Li2(z) | Li3(z) |
Propriétés
Dans le cas important où le paramètre s est un nombre entier, il sera représenté par n (ou -n lorsqu'il est négatif). Il est souvent pratique de définir μ = ln(z) où ln est la branche principale du logarithme naturel, c’est-à-dire . Ainsi, toute l'exponentiation sera supposée être à valeur unique. (e.g. zs = es ln(z)).
Dépendant du paramètre s, le polylogarithme peut être à valeurs multiples. La branche principale du polylogarithme est celle pour laquelle Lis(z) est réel pour z réel, 0 ≤ z ≤ 1 et est continu excepté sur l'axe des réels positifs, où une coupure est faite de z = 1 à l'infini telle que la coupure place l'axe réel sur le demi-plan le plus bas de z. En termes de μ, ceci s'élève à –π < arg(–μ) < π. Le fait que le polylogarithme puisse être discontinu en μ peut causer une certaine confusion.
Pour z réel et supérieur ou égal à 1, la partie imaginaire du polylogarithme est (Wood 1992) :
En traversant la coupure :
Les dérivées du polylogarithme s'expriment également avec le polylogarithme :
Valeurs particulières

Voir aussi la section « Relation de parenté avec les autres fonctions » ci-dessous.
Pour les valeurs entières de s, on peut écrire les expressions explicites suivantes :
Le polylogarithme, pour toutes les valeurs entières négatives de s, peut être exprimé comme une fraction rationnelle en z (voir les représentations en série ci-dessus). Certaines expressions particulières pour les demi valeurs entières de l'argument sont :
où est la fonction zêta de Riemann. Aucune formule similaire de ce type n'est connue pour des ordres plus élevés (Lewin 1991, p. 2) ; par ailleurs, les seules valeurs connues de Li2 exprimables à l'aide des fonctions élémentaires sont les huit valeurs suivantes[1] :
ainsi que
- ;
- .
Expressions alternatives
- L'intégrale de la distribution de Bose-Einstein est exprimée en termes de polylogarithme :
- Celle-ci converge pour et tous les z excepté pour les z réels et supérieurs ou égaux à 1. Le polylogarithme dans ce contexte est quelquefois connu comme l'intégrale de Bose ou de Bose-Einstein.
- L'intégrale de la distribution de Fermi-Dirac est aussi exprimée en termes de polylogarithme :
- Celle-ci converge pour et tous les z excepté pour les z réels et strictement inférieurs à -1. Le polylogarithme dans ce contexte est quelquefois connu comme l'intégrale de Fermi ou l'intégrale de Fermi-Dirac. (GNU)
- Le polylogarithme peut plutôt être généralement représenté par une intégrale sur un contour de Hankel (en) (Whittaker et Watson 1927).
- Tant que le pôle t = μ de l'intégrande n'est pas relié à l'axe réel positif, et , on a :
- où H représente le contour de Hankel. L'intégrande possède une coupure le long de l'axe réel de zéro à l'infini, l'axe réel étant sur la moitié inférieure de la feuille ().
- Pour le cas où μ est réel et positif, nous pouvons simplement ajouter la contribution limitante du pôle :
- où R est le résidu du pôle :
- Tant que le pôle t = μ de l'intégrande n'est pas relié à l'axe réel positif, et , on a :
- La relation carrée est facilement vue à partir de l'équation (voir aussi Clunie 1954 et Schrödinger 1952)
- La fonction de Kummer obéit à une formule de duplication très similaire.
Relation de parenté avec les autres fonctions
- Pour z = 1, le polylogarithme se réduit à la fonction zêta de Riemann
- Le polylogarithme est relié à la fonction êta de Dirichlet et la fonction bêta de Dirichlet :
- où η(s) est la fonction êta de Dirichlet.
- Pour des arguments imaginaires purs, nous avons :
- où β(s) est la fonction bêta de Dirichlet.
- Le polylogarithme est équivalent à l'intégrale de Fermi-Dirac (GNU)
- Le polylogarithme est un cas particulier de la fonction transcendante de Lerch (Erdélyi et al. 1981, § 1.11-14)
- Le polylogarithme est relié à la fonction zêta de Hurwitz par :
- où Γ(s) est la fonction Gamma d'Euler. Ceci est valable pour
et aussi pour
- (l'équation équivalente d'Erdélyi et al. 1981, § 1.11-16 n'est pas correcte si on suppose que les branches principales du polylogarithme et le logarithme sont utilisés simultanément).
- Cette équation fournit le prolongement analytique de la représentation en série du polylogarithme au-delà de son cercle de convergence |z| = 1.
- En utilisant la relation entre la fonction zêta de Hurwitz et les polynômes de Bernoulli :
- qui reste valable pour tous les x réels et n entier positif, il peut être remarqué que :
- sous les mêmes contraintes sur s et x que ci-dessus. (L'équation correspondante d'Erdélyi et al. 1981, § 1.11-18 n'est pas correcte). Pour les valeurs entières négatives du paramètre, on a pour tous les z (Erdélyi et al. 1981, § 1.11-17) :
- Le polylogarithme avec un μ imaginaire pur peut être exprimé en termes de fonctions de Clausen Cis(θ) et Sis(θ) (Lewin 1958, ch. VII, § 1.4 et Abramowitz & Stegun, § 27.8)
- La fonction tangente intégrale inverse (en) Tis(z) (Lewin 1958, ch. VII, § 1.2) peut être exprimée en termes de polylogarithmes :
- La fonction chi de Legendre χs(z) (Lewin 1958, ch VII, § 1.1 et Boersma et Dempsey 1992) peut être exprimée en termes de polylogarithmes :
- Le polylogarithme peut être exprimé comme une série de fonctions de Debye Zn(z) (Abramowitz & Stegun, § 27.1)
- Une expression remarquablement similaire relie la fonction de Debye au polylogarithme :
Représentations en séries
On peut représenter le polylogarithme comme une série de puissances pour μ = 0 comme suit (Robinson 1951). Considérons la transformation de Mellin :
Le changement de variables t = ab, u = a(1-b) permet à l'intégrale d'être séparée :
pour f = 1 on a, à travers la transformation inverse de Mellin :
où c est une constante à droite des pôles de l'intégrande.
Le chemin d'intégration peut être converti en un contour fermé, et les pôles de l'intégrande sont ceux de Γ(r) à r = 0 , –1, –2, … et de ζ(s+r) à r = 1–s. Sommer les résidus donne, pour et
Si le paramètre s est un entier positif n, ainsi que le k = n–1e terme, la fonction gamma devient infinie, bien que leur somme ne l'est pas. Pour un entier k > 0, nous avons :
et pour k = 0 :
Ainsi, pour s = n où n est un entier positif et , nous avons :
où Hn-1 est un nombre harmonique :
Le problème des termes contient maintenant -ln(-μ) qui, lorsqu'ils sont multipliés par μk, tendront vers zéro quand μ tend vers zéro, excepté pour k = 0. Ceci reflète le fait qu'il existe une vraie singularité logarithmique en Lis(z) en s = 1 et z = 1, puisque :
En utilisant la parenté entre la fonction zêta de Riemann et les nombres de Bernoulli Bk
on obtient pour les valeurs entières négatives de s et :
puisque, excepté pour B1, tous les nombres de Bernoulli impairs sont égaux à zéro. Nous obtenons le terme n = 0 en utilisant . Encore, l'équation équivalent d'Erdélyi et al. 1981, § 1.11-15 n'est pas correcte si nous supposons que les branches principales du polylogarithme et le logarithme sont utilisées simultanément, puisque n'est pas uniformément égal à –ln(z).
L'équation définie peut être étendue aux valeurs négatives du paramètre s en utilisant une intégrale sur un contour de Hankel (en) (Wood 1992 et Gradshteyn et Ryzhik 1980) :
où H est le contour de Hankel qui peut être modifié pour qu'il entoure les pôles de l'intégrande, à t – μ = 2kiπ, l'intégrale peut être évaluée comme la somme des résidus :
Ceci restera valable pour et tous les z excepté pour z = 1.
Pour les entiers négatifs s, le polylogarithme peut être exprimé comme une série impliquent les nombres eulériens
où sont les nombres eulériens.
Une autre formule explicite pour les entiers négatifs s est (Wood 1992) :
où S(n,k) sont les nombres de Stirling de deuxième espèce.
Comportement aux limites
Les limites suivantes restent valables pour le polylogarithme (Wood 1992) :
Échelles de polylogarithmes
Leonard Lewin a découvert une remarquable généralisation d'un grand nombre de relations classiques sur les polylogarithmes pour des valeurs particulières. Celles-ci sont maintenant appelées les échelles de polylogarithmes. Définissons comme l'inverse du nombre d'or. Alors, deux exemples simples des résultats issus des échelles incluent
donné par Coxeter en 1935, et[2]
donné par Landen. Les échelles de polylogarithmes apparaissent naturellement et profondément en K-théorie.
Notes et références
- Zagier 2006 p. 6
- G.Huvent, Autour de la primitive de , 2002
- (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne)
- (en) J. Boersma et J. P. Dempsey, « On the evaluation of Legendre's chi-function », Math. Comp., vol. 59, no 199, , p. 157-163
- (en) J. Clunie, « On Bose-Einstein functions », Proc. Phys. Soc. Section A, vol. 67, , p. 632-636
- (en) A. Erdélyi (en), W. Magnus, F. Oberhettinger (de) et F. G. Tricomi, Higher Transcendental Functions, vol. 1, New York, Krieger,
- (en) I. S. Gradshteyn et I. M. Ryzhik, Tables of Integrals, Series, and Products, New York, Academic Press, , § 9.553
- (en) L. Lewin, Dilogarithms and Associated Functions, London, Macdonald,
- (en) Leonard Lewin, Structural Properties of Polylogarithms, [détail de l’édition]
- (en) J. E. Robinson, « Note on the Bose-Einstein integral functions », Physical Review, 2e série, vol. 83, , p. 678-679 (lire en ligne)
- (en) E. Schrödinger, Statistical Thermodynamics, Cambridge,
- (en) E. T. Whittaker et G. N. Watson, A Course of Modern Analysis, Cambridge, , § 12.22 et 13.13
- (en) David C. Wood, Technical Report 15-92, Canterbury, UK, University of Kent Computing Laboratory, (lire en ligne)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Polylogarithm » (voir la liste des auteurs).
Bibliographie
- (en) David Bailey, Peter Borwein et Simon Plouffe, « On the Rapid Computation of Various Polylogarithmic Constants », Math. Comp., vol. 66, no 218, , p. 903–913 (lire en ligne)
- (en) David H. Bailey et David J. Broadhurst, « A Seventeenth-Order Polylogarithm Ladder », 1999, « math.CA/9906134 », texte en accès libre, sur arXiv.
- (en) Jonathan M. Borwein, David M. Bradley, David J. Broadhurst et Petr Lisonek, « Special Values of Multidimensional Polylogarithms », Trans. Amer. Math. Soc., vol. 353, , p. 907-941 (lire en ligne), « math.CA/9910045 », texte en accès libre, sur arXiv.
- (en) B. C. Berndt, Ramanujan's Notebooks, Part IV, Springer, , p. 323-326
- (en) B. Fornberg et K. S. Kölbig, « Complex zeros of the Jonquiére or polylogarithm function », Math. Comp., vol. 29, no 130, , p. 582-599
- (en) GNU Scientific Library, Reference Manual
- (en) Eugen Jahnke et Fritz Emde (de), Tables of Functions with Formulae and Curves, Dover,
- (en) K. S. Kölbig, J. A. Mignaco et E. Remiddi, « On Nielsen's generalized polylogarithms and their numerical calculation », BIT, vol. 10, , p. 38-74
- (en) K. S. Kölbig, « Nielsen's Generalized Polylogarithms », SIAM J. Math. Anal., vol. 17, , p. 1232-1258
- (en) L. Lewin, Polylogarithms and Associated Functions, North-Holland,
- (en) J. McDougall et E. C. Stoner (en), « The computation of Fermi-Dirac functions », Philos. Trans. Royal Soc., Series A, vol. 237, , p. 67-104 (lire en ligne)
- (en) B. Markman, « The Riemann Zeta Function », BIT, vol. 5, , p. 138-141
- (de) N. Nielsen (de), « Der Eulersche Dilogarithmus und seine Verallgemeinerungen », Nova Acta Leopoldina, vol. 90, , p. 123-211
- (en) A. P. Prudnikov, O. I. Marichev (de) et Yu. A. Brychkov, The Generalized Zeta Function, Bernoulli Polynomials, Euler Polynomials, and Polylogarithms, Vol. 3: More Special Functions, Gordon and Breach, , p. 23-24, § 1.2
- (en) C. Truesdell, « On a function which occurs in the theory of the structure of polymers », Ann. of Math., 2e série, vol. 46, no 1, , p. 144-1457
- (en) Don Zagier, « Appendix A : Special Values and Functional Equations of Polylogarithms », dans L. Lewin (éd.), Structural Properties of Polylogarithms, AMS,
- (en) Don Zagier, « The Dilogarithm Function », dans P. Cartier, B. Julia, P. Moussa, P. Vanhove (éds.), Frontiers in Number Theory, Physics and Geometry II, Springer-Verlag, (lire en ligne)












![{\displaystyle \operatorname {Li} _{3}\left({\frac {1}{2}}\right)={1 \over 24}[4(\ln 2)^{3}-2\pi ^{2}\ln 2+21\,\zeta (3)]}](https://img.franco.wiki/i/9563619bb4b779dcfa3b0cf37a1dd80f6fd3cc0b.svg)


























![{\displaystyle \chi _{s}(z)={1 \over 2}~[\operatorname {Li} _{s}(z)-\operatorname {Li} _{s}(-z)]}](https://img.franco.wiki/i/fa3ce71ab37c50ca19668e3fab1e9302e4fa98ee.svg)








![{\displaystyle \lim _{s\rightarrow k+1}\left[{\zeta (s-k)\mu ^{k} \over k!}+\Gamma (1-s)(-\mu )^{s-1}\right]={\mu ^{k} \over k!}\left(\sum _{m=1}^{k}{1 \over m}-\ln(-\mu )\right)}](https://img.franco.wiki/i/84de5f56a6cf77588f996308352cda85a2e144f4.svg)
![{\displaystyle \lim _{s\rightarrow 1}\left[\zeta (s)+\Gamma (1-s)(-\mu )^{s-1}\right]=-\ln(-\mu )}](https://img.franco.wiki/i/ffd15f2027e0bcb8afa1febba88fa255e1cb657e.svg)





















