Fonction de Clausen
En mathématiques , la fonction de Clausen , étudiée par Clausen puis (entre autres) Kummer et Rogers (en)
Cl
2
(
θ
)
=
−
∫
0
θ
ln
|
2
sin
(
t
/
2
)
|
d
t
{\displaystyle \operatorname {Cl} _{2}(\theta )=-\int _{0}^{\theta }\ln |2\sin(t/2)|\,\mathrm {d} t}
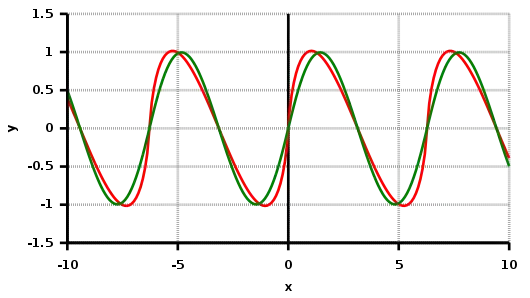
Graphe des fonctions de Clausen Cl2 (rouge) et Cl4 (vert).
Plus généralement, on définit, pour Re(s ) > 1
Cl
s
(
θ
)
=
∑
n
=
1
∞
sin
(
n
θ
)
n
s
{\displaystyle \operatorname {Cl} _{s}(\theta )=\sum _{n=1}^{\infty }{\frac {\sin(n\theta )}{n^{s}}}}
Propriétés Les fonctions de Clausen sont impaires et 2π -périodiques , donc nulles sur π ℤ .
Cl
2
(
θ
)
=
∫
0
π
−
θ
ln
|
2
cos
(
s
/
2
)
|
d
s
{\displaystyle \operatorname {Cl} _{2}(\theta )=\int _{0}^{\pi -\theta }\ln |2\cos(s/2)|\,\mathrm {d} s}
La fonction Cln pour n ∈ ℕ*polylogarithme Lin par :
∀
m
∈
N
∗
Cl
2
m
(
θ
)
=
Im
(
Li
2
m
(
e
i
θ
)
)
{\displaystyle \forall m\in \mathbb {N} ^{*}\quad \operatorname {Cl} _{2m}(\theta )=\operatorname {Im} (\operatorname {Li} _{2m}(\mathrm {e} ^{\mathrm {i} \theta }))}
∀
m
∈
N
Cl
2
m
+
1
(
θ
)
=
Re
(
Li
2
m
+
1
(
e
i
θ
)
)
{\displaystyle \forall m\in \mathbb {N} \quad \operatorname {Cl} _{2m+1}(\theta )=\operatorname {Re} (\operatorname {Li} _{2m+1}(\mathrm {e} ^{\mathrm {i} \theta }))}
Pour tout entier m ≥ 2
Cl
m
(
2
θ
)
=
2
m
−
1
(
Cl
m
(
θ
)
−
(
−
1
)
m
Cl
m
(
π
−
θ
)
)
{\displaystyle \operatorname {Cl} _{m}(2\theta )=2^{m-1}{\Bigl (}\operatorname {Cl} _{m}(\theta )-(-1)^{m}\operatorname {Cl} _{m}(\pi -\theta ){\Bigr )}}
Li
2
(
exp
(
i
θ
)
)
=
ζ
(
2
)
−
θ
(
2
π
−
θ
)
/
4
+
i
Cl
2
(
θ
)
{\displaystyle \operatorname {Li} _{2}(\exp(\mathrm {i} \theta ))=\zeta (2)-\theta (2\pi -\theta )/4+\mathrm {i} \operatorname {Cl} _{2}(\theta )}
pour 0 ≤ θ ≤ 2π , où ζ est la fonction zêta de Riemann [1]
Accélération du calcul de la série Une des accélérations de série de la fonction de Clausen est donnée par :
Cl
2
(
θ
)
θ
=
1
−
ln
|
θ
|
+
∑
n
=
1
∞
ζ
(
2
n
)
n
(
2
n
+
1
)
(
θ
2
π
)
2
n
{\displaystyle {\frac {\operatorname {Cl} _{2}(\theta )}{\theta }}=1-\ln |\theta |+\sum _{n=1}^{\infty }{\frac {\zeta (2n)}{n(2n+1)}}\left({\frac {\theta }{2\pi }}\right)^{2n}}
pour |θ | < 2π .
Une forme convergeant plus rapidement est donnée par :
Cl
2
(
θ
)
θ
=
3
−
ln
[
|
θ
|
(
1
−
θ
2
4
π
2
)
]
−
2
π
θ
ln
(
2
π
+
θ
2
π
−
θ
)
+
∑
n
=
1
∞
ζ
(
2
n
)
−
1
n
(
2
n
+
1
)
(
θ
2
π
)
2
n
{\displaystyle {\frac {\operatorname {Cl} _{2}(\theta )}{\theta }}=3-\ln \left[|\theta |\left(1-{\frac {\theta ^{2}}{4\pi ^{2}}}\right)\right]-{\frac {2\pi }{\theta }}\ln \left({\frac {2\pi +\theta }{2\pi -\theta }}\right)+\sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{n(2n+1)}}\left({\frac {\theta }{2\pi }}\right)^{2n}}
La rapidité de la convergence de cette série est due au fait que ζ(n ) tend rapidement vers 1 quand n tend vers l'infini. Ces deux formes sont générées grâce aux techniques de somme utilisées pour obtenir la série zêta rationnelle [2]
Valeurs particulières
Cl
2
(
π
2
)
=
K
{\displaystyle \operatorname {Cl} _{2}\left({\frac {\pi }{2}}\right)=K}
où K est la constante de Catalan . Plus généralement :
Cl
s
(
π
2
)
=
β
(
s
)
{\displaystyle \operatorname {Cl} _{s}\left({\frac {\pi }{2}}\right)=\beta (s)}
où β est la fonction bêta de Dirichlet .
La valeur maximale de Cl2 est la constante de Gieseking (de) [3] [4]
G
=
Cl
2
(
π
3
)
=
3
2
Cl
2
(
2
π
3
)
≈
1,015
{\displaystyle \mathrm {G} =\operatorname {Cl} _{2}\left({\frac {\pi }{3}}\right)={\frac {3}{2}}\operatorname {Cl} _{2}\left({\frac {2\pi }{3}}\right)\approx 1{,}015}
Le volume hyperbolique (en) complément du nœud en huit (en) [5] [6]
V
=
2
G
=
2
3
∑
n
=
1
∞
1
n
(
2
n
n
)
∑
k
=
n
2
n
−
1
1
k
≈
2
,
03
{\displaystyle V=2\mathrm {G} =2{\sqrt {3}}\,\sum _{n=1}^{\infty }{\frac {1}{n{\binom {2n}{n}}}}\sum _{k=n}^{2n-1}{\frac {1}{k}}\approx 2{,}03}
A091518 [7]
Références (en) Leonard Lewin , Structural Properties of Polylogarithms , 1991 [ détail de l’édition] p. 8 . (en) Jonathan M. Borwein , David M. Bradley et Richard E. Crandall , « Computational Strategies for the Riemann Zeta Function » , J. Comput. App. Math. vol. 121, nos 1-2, 2000 , p. 247-296 (DOI 10.1016/S0377-0427(00)00336-8 (en) Eric W. Weisstein , « Gieseking's Constant MathWorld Apparaît sous le nom de « constante de Lobachevsky » dans (en) Steven Finch, « Volumes of Hyperbolic 3-Manifolds » Université Harvard 2004 , p. 4 . Finch 2004 , p. 3-4 . (en) Jonathan Borwein et David Bailey , Mathematics by Experiment : Plausible Reasoning in the 21st Century , A K Peters , 2008 , 393 p. (ISBN 978-1-56881-442-1 , lire en ligne ) , p. 56 Pour de nombreuses autres expressions de V , voir (en) Eric W. Weisstein , « Figure Eight Knot MathWorld
Voir aussi
Cet article est issu de
wikipedia . Text licence:
CC BY-SA 4.0 , Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.








![{\displaystyle {\frac {\operatorname {Cl} _{2}(\theta )}{\theta }}=3-\ln \left[|\theta |\left(1-{\frac {\theta ^{2}}{4\pi ^{2}}}\right)\right]-{\frac {2\pi }{\theta }}\ln \left({\frac {2\pi +\theta }{2\pi -\theta }}\right)+\sum _{n=1}^{\infty }{\frac {\zeta (2n)-1}{n(2n+1)}}\left({\frac {\theta }{2\pi }}\right)^{2n}}](https://img.franco.wiki/i/8e8fcbf6de4474a4247011a217ac1699f06f14fd.svg)



