Dynamique des populations
La dynamique des populations est une branche de l'écologie qui s’intéresse à la fluctuation dans le temps du nombre d'individus au sein d'une population d’êtres vivants. Elle a également pour but de comprendre les influences environnementales sur les effectifs des populations. La structuration de la population par âge, poids, l'environnement, la biologie des groupes, et les processus qui influent sur ces changements font également partie de son champ d'étude. Des applications emblématiques incluent la pêche, la gestion cynégétique, la gestion des zones protégées, le contrôle des populations d'animaux dits nuisibles. La dynamique des populations humaines ainsi que leurs spécificités par rapport aux autres populations animales sont étudiées par la science démographique.
Types de dynamiques
Il est possible de distinguer de grandes familles de dynamique des populations en fonction de leur comportement en l'absence de perturbations. Cette classification est étroitement liée à la théorie mathématique des systèmes dynamiques et à la notion d'attracteur.
Dynamique stable
- Population stationnaire : la population tend vers une distribution des âges constante, indépendante des conditions initiales. Cela correspond au cas d'un attracteur ponctuel
Dynamique cyclique
- Cyclique : la population présente des fluctuations saisonnières (flux migratoires), annuelles voire pluriannuelles (par exemple les populations de lemmings et de leurs prédateurs comme le harfang des neiges et le renard polaire).
Dynamique chaotique
La dynamique chaotique des populations correspond à la variation non prédictible du nombre d’individus d’une population au cours du temps. Cette variation est due aux taux de croissance intrinsèques élevés des populations et à une sensibilité aux conditions initiales[1], ce qui peut avoir des conséquences écologiques mais aussi évolutives. Les dynamiques chaotiques peuvent être observées à travers différents modèles, des plus simples aux plus complexes (même pour des systèmes déterministes). Il est important de préciser l'échelle de temps de la modélisation.
Perturbations écologiques
Les perturbations écologiques typiques de la dynamique des populations incluent :
- les invasions biologiques, qui peuvent être ponctuelles ou invasions récurrentes et plus ou moins régulières (de criquets pèlerins par exemple) ;
- les perturbations d'origine anthropiques et pouvant conduire à des disparitions massive d'espèces ou de populations, en raison des excès de chasse, pêche, brûlage, etc. Ainsi peut-on spécifiquement étudier les dynamiques de « populations exploitées » ou surexploitées (dans le cadre de la gestion durable des pêches par exemple[2]). C'est par ce type d'étude qu'on a montré que la pêche en mer pouvait considérablement influencer la taille, la composition et la diversité des poissons démersaux[3].
Modélisation mathématique
Bilan démographique
On note « Nt » le nombre d'individus dans une population donnée à un temps t.
La variation du nombre d'individus lors d'une période Δt (une heure, un an…) peut être décomposée sous la forme :
Avec :
- n, le nombre de naissances lors de Δt ;
- m, le nombre de morts lors de Δt ;
- i, le nombre d'individus qui immigrent dans la population lors de Δt ;
- e, le nombre d'individus qui émigrent de la population lors de Δt.
On parle de bilan démographique : n-m constitue le solde naturel et i-e le solde migratoire de la population.
Outils mathématiques
En temps discret, on peut modéliser une population par une suite[4] (déterministe) ou une chaîne de Markov (voir processus de naissance et de mort).
Dans de nombreux cas, la modélisation est plus aisée en temps continu , on utilise alors des équations différentielles. On note N(t) le nombre d'individus dans une population donnée au temps t et on utilise la dérivée temporelle de N, , pour représenter la variation instantanée du nombre d'individus.
| Déterministe | Stochastique | |
|---|---|---|
| Temps discret | Suite | Chaîne de Markov |
| Temps continu | Équations différentielles | Processus de Markov à temps continu |
Modèles de dynamiques de populations
Pour modéliser il est important de préciser l'échelle de temps utilisée. Par exemple, la population de coquelicots dans un champ pourra être qualifiée de stable sur trois ou quatre ans, mais à l'échelle d'une année la population varie énormément. Ainsi on peut parler de temps discret ou continu.
Croissance géométrique et exponentielle
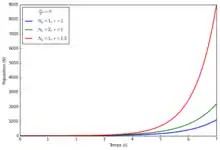
Les modèles de croissance géométrique et exponentielle supposent un taux de croissance proportionnel au nombre d'individus. On parle parfois de croissance Malthusienne en référence aux travaux de l'économiste Thomas Malthus. Leur dynamique est assez simple et peu réaliste: la population croît indéfiniment, cependant leurs prédictions peuvent se révéler correctes sur des temps courts. Ils servent de base à des modèles plus sophistiqués comme les modèles matriciels de populations pour étudier la dynamique des populations structurées.
Soit une population au solde migratoire nul (e+i=0). On considère que le nombre de naissances (n) et de morts (m) est dépendant du nombre d'individus.
Si l'on considère cette dépendance comme linéaire (la proportionnalité mentionnée plus haut), en notant λ le taux de naissances et μ le taux de mortalité (c'est-à-dire le nombre de naissances -respectivement de morts- par individu lors de Δt.
En temps discret, l'évolution du nombre d'individus peut être modélisée par une suite géométrique de raison r=1+λ-μ.
En temps continu, l'effectif de la population peut être modélisé par l'équation différentielle ordinaire suivante:
Croissance logistique
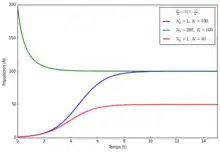
Les modèles de croissance logistique sont un premier raffinement des modèles Malthusiens dans lequel le taux de croissance de la population sature avec le nombre d'individus, ainsi la population ne peut pas atteindre une taille infinie : elle est limitée par une taille maximale appelée capacité biotique. La valeur de la capacité biotique dépend de l'environnement dans lequel évolue la population, elle est généralement liée à un épuisement des ressources.
En temps discret, l'effectif de la population peut être modélisé par la suite logistique qui a la particularité d'exhiber une dynamique chaotique pour certaines valeurs de paramètres :
L'équivalent en temps continu est le modèle de Verhulst:
Dans les deux cas, la population possède deux points d'équilibre en 0 (extinction) et en K (population stationnaire). Le modèle de croissance logistique en temps continu a pour particularité que toute population strictement positive (même constituée d'une impossible « fraction d'individu ») tend vers sa capacité biotique K. Ce problème est souvent corrigé en ajoutant un terme d'effet Allee.
Du prévisible au chaotique
Une population présentant une dynamique stable ou cyclique peut évoluer vers une dynamique chaotique. Cette évolution pourrait être due à des changements des conditions environnementales, à des phénomènes de prédation ou de dispersion[5]. Cette transition a été décrite mathématiquement par plusieurs modèles qui en fonction des paramètres qu’ils étudient (dispersion, prédation, conditions environnementales) mènent à des dynamiques chaotiques.
Modèle en temps continu : Verhulst et Feigenbaum
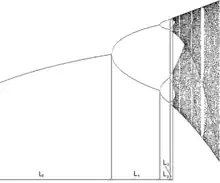
Ce modèle a été initialement découvert par Verhulst en 1840. Près d’un siècle plus tard, le physicien Mitchell Feigenbaum a étudié les solutions quasi cycliques de ce modèle. Pour décrire le passage d’une dynamique périodique à une dynamique chaotique, Mitchell Feigenbaum a établi une trajectoire appelée « cascade de doublement de période » (voir théorie du chaos). Ce modèle représenté par le diagramme de bifurcation présente donc les successions des dynamiques en fonction du taux de croissance intrinsèque des populations noté r.
On obtient donc les interprétations suivantes :
- r = 3, la population est dite stable. On a ainsi une oscillation amortie entre une valeur minimum et une valeur maximum. Ces deux valeurs correspondent aux états dits stationnaires.
- 3 < r < 3,569, la population présente des cycles périodiques. On a d’abord 2 états stationnaires puis 4 avec 2 valeurs minimum et 2 valeurs maximum
- r = 3,569 : le “point de Feigenbaum” est atteint et la dynamique devient chaotique présentant des oscillations imprédictibles.
- r > 3,569 : la population présente une dynamique chaotique avec la cascade de dédoublement: d’abord 8 états stationnaires puis 12, puis 16, puis 32 et ainsi de suite
Modèle en temps discret : Ricker
C’est un modèle simple qui cherche également à analyser le passage d’une dynamique stable ou cyclique à une dynamique chaotique en temps discret : il décrit le nombre d’individus dans une population à t+1 par rapport au nombre d’individus de cette même population au temps t.
Ce modèle s'écrit :
On obtient alors la même structure de graphique, c’est-à-dire un diagramme de bifurcation, que pour un modèle en temps continu, mais présentant des variations à des taux de croissance r différents.
On obtient ici les interprétations suivantes :
- 0< r < 2, la population est stable et présente un état stationnaire.
- 2 < r < 2,692, la population présente une dynamique cyclique et oscille entre 2 états stationnaires.
- r > 2,692, la dynamique de la population devient chaotique et oscille d’abord entre 4 états stationnaires, puis applique la cascade de dédoublement avec 8 états stationnaires, puis 12, puis 16, puis 32 et ainsi de suite. La longueur des intervalles entre ces phénomènes de dédoublement diminue quand r augmente.
Remarques
Entre deux événements chaotiques, il est possible d’observer des retours à une dynamique cyclique grâce à des attracteurs étranges (voir: théorie du chaos).
Dans les périodes chaotiques, la moindre variation des valeurs initiales aura un impact très fort sur la prévision des valeurs futures à l’inverse des dynamiques stables et cycliques. Cette instabilité peut être résumée par cette question de Lorenz Edward : « Le battement d’ailes d’un papillon au Brésil provoque-t-il une tornade au Texas ? ».
Les dynamiques chaotiques présentent donc un caractère non prévisible sur le long terme, on parle d’”effet papillon”.
Lorsque l’on se retrouve dans un environnement stochastique, une dynamique chaotique peut de façon aléatoire mener à l’extinction, à l’invasion par des mutants ou au maintien de la population. Cependant, le chaos est très rare dans les milieux naturels, donc la probabilité de voir l’extinction d’une population due au chaos est très faible. Certains chercheurs suggèrent même que le comportement chaotique pourrait conférer un avantage évolutif[6] ce qui permettrait aux mutants d’envahir des populations.
Chaos à travers l'expérimentation
Il existe assez peu d’expériences démontrant les dynamiques chaotiques au sein d’une population[7]. Ces expériences ont cherché à confronter les modèles mathématiques aux différents types de dynamiques (stable, cyclique ou chaotique) que l’on peut trouver dans la nature. Or, ces formules y sont peu applicables. Les communautés utilisées sont choisies pour leur simplicité : écosystèmes réduits à 3 espèces maximum dont les taux de croissance et de reproduction sont très réduits afin que les expériences soient rapides ; facteurs externes à la population négligés[8]. Dans la nature, les conditions environnementales sont fluctuantes, les chaînes trophiques sont souvent complexes et les taux de croissance/reproduction bien moins rapide donc ces expériences ne sont pas représentatives.
Les conditions environnementales menant au chaos sont donc rarement réunies dans la nature[9]. En effet, pour observer une dynamique chaotique lors d’une phase stationnaire il faut avoir eu une longue période de stabilité des conditions environnementales au cours de la phase transitoire. Contrairement aux mathématiciens, les écologues ont un avis mitigé sur l’existence du chaos dans la nature.
Espèces en compétition
Une seconde extension des modèles précédent introduit la dynamique couplée de multiples espèces. Un représentant assez classique de cette famille de modèles sont les équations de compétition de Lotka-Volterra :
- N1 (respectivement N2) est le nombre d'individus de la première (respectivement seconde) espèce, et leur taux de croissance r1 (respectivement r2) et capacité biotique K1 (respectivement K2). Le terme de compétition α12 représente l'effet de l'espèce 2 sur la population de l'espèce 1, et réciproquement pour α21 .
En fonction des paramètres ce modèle conduit à l'extinction d'une des deux espèces, à une dynamique cyclique ou à la convergence du système vers un point d'équilibre où les deux espèces survivent. La théorie moderne de la coexistence utilise ce modèle pour développer les outils mathématiques nécessaires à la prédiction de la coexistence dans les situations où il y a plus de deux espèces.
Applications
Démographie humaine
En sciences sociales, la démographie se réserve l’étude des populations humaines, qui diffèrent des populations animales non pas tant par les valeurs des paramètres biologiques (durée de vie, intervalle entre générations, etc.), que par la conscience qu’en a chaque individu, et qui permet l’interrogation des intéressés. Les individus ont un âge, c’est-à-dire une date de naissance. Ils sont les sujets d'événements, tels que mariage et procréation, dont le repérage suppose soit une enquête auprès des intéressés (recensement ou sondage), soit des institutions appropriées (état civil). Ce repérage exige que soit connu le nom des individus, qui disparaît ensuite dans le traitement des données. Les relevés des lieux de naissance, de séjour, de décès, supposent également, notamment pour l’étude des migrations, un découpage géographique reconnu. La qualité et le progrès des connaissances démographiques dépendent donc des institutions administratives nécessaires à la collecte des données et à la garantie du secret.
L’étude de la précision des effectifs de populations humaines, obtenus par enquête ou par calcul, ou celle de la datation des événements démographiques, en particulier naissances et décès, met ainsi en jeu la psychologie des individus, leur confiance ou leur méfiance envers les enquêteurs et agents recenseurs, leur mémoire sélective des événements familiaux, leur degré d’adhésion aux institutions classificatoires.
La théorie de la Transition démographique permet d'expliquer l'évolution de la population mondiale de 1800 à 2100
Notes et références
- (en) R.M May, « Biological populations with nonoverlapping generations: stable points, stable cycles, and chaos », Science,
- Beverton R.J.H., Holt S.J.On the dynamics of exploited fish populations. Fishery Investigations, Series II 1957;19:1-533.
- Bianchi G., Gislason H., Graham K., Hill L., Jin X., Koranteng K., Manickchand-Heileman S., Paya I., Sainsbury K., Sanchez F., Zwanenburg K., Impact of fishing on size composition and diversity of demersal fish communities. ICES Journal of Marine Science 2000;57:558-571 (résumé).
- Alain Hillion, Les théories mathématiques des populations, Paris, P.U.F., coll. « Que sais-je ?, n°2258 », , 127 p. (ISBN 2-13-039193-1)
- (en) R.D, Holt, « Chaotic population dynamics favors the evolution of dispersal », The American Naturalist,
- (en) M. Doebeli, « The evolutionary advantage of controlled chaos », Proceedings of the Royal Society of London B: Biological Sciences,
- (en) R.F Costantino, « Chaotic dynamics in an insect population », Science,
- (en) L. Becks, « Experimental demonstration of chaos in a microbial food web », Nature,
- (en) K. Mcann, « Biological Conditions for Chaos in a Three‐Species Food Chain », Ecology,
Voir aussi
Bibliographie
- (en) Ted. J. Case, An Illustrated Guide to Theoretical Ecology, Oxford University Press, 2000
- Vito Volterra, Leçons sur la théorie mathématique de la lutte pour la vie, Gauthier-Villars, 1931 ; réimpr. Jacques Gabay, 1990
- Alfred J. Lotka, Théorie analytique des associations biologiques, Hermann, 1934/1939
- Alain Hillion, Les théories mathématiques des populations, PUF, coll. « Que sais-je ? » (no 2258), 1986
- Nicolas Bacaër, Histoires de mathématiques et de populations, Cassini, 2009
- Pierre Auger, Christophe Lett et Jean-Christophe Poggiale, Modélisation mathématique en écologie, Dunod, 2010
- (en) James D. Murray, Mathematical Biology, Springer-Verlag, 3e éd. en deux volumes : Mathematical Biology: I. An Introduction, 2002 (ISBN 0-387-95223-3) ; Mathematical Biology: II. Spatial Models and Biomedical Applications, 2003 (ISBN 0-387-95228-4).
- (en) Mimmo Iannelli et Andrea Pugliese, An Introduction to Mathematical Population Dynamics, Cham, Springer International Publishing Switzerland, (ISBN 978-3-319-03025-8, lire en ligne).










