Onde gravitationnelle
Onde de gravitation

En physique, une onde gravitationnelle, appelée parfois onde de gravitation, est une oscillation de la courbure de l'espace-temps qui se propage à grande distance de son point de formation.
Albert Einstein a prédit l'existence des ondes gravitationnelles en : selon sa théorie de la relativité générale qu’il venait de publier, de même que les ondes électromagnétiques (lumière, ondes radio, rayons X, etc.) sont produites par les particules chargées accélérées, les ondes gravitationnelles seraient produites par des masses accélérées et se propageraient à la vitesse de la lumière dans le vide. Cependant, la réalité des ondes gravitationnelles a été longuement débattue. Einstein changea plusieurs fois d'avis à ce sujet, la question étant de savoir si ces ondes avaient effectivement une existence physique ou bien constituaient un artefact mathématique résultant d'un choix du système de coordonnées. Pour statuer, et disposer à cette occasion d'un nouveau test de la relativité générale, seule la recherche expérimentale pouvait lever le doute. Les efforts dans ce sens ont été engagés à partir des années 1960, avec la réalisation des premières barres de Weber.
Depuis , l'existence des ondes gravitationnelles est confirmée, grâce à une première observation faite le . Cette observation ouvre un champ nouveau d'observation de l'univers à grande échelle, d'autant que les ondes gravitationnelles ne sont pas arrêtées par la matière. En revanche elle laisse encore ouverte la question de l’existence du graviton.
Le succès des détecteurs interférométriques à détecter un déplacement maximal de ± 2 × 10−18 m permet, en 2016, d'espérer un élargissement du spectre d'observation avec les développements techniques à venir.
Historique
Prédiction
Les principes de la relativité restreinte amènent à postuler que l'interaction gravitationnelle se propage (au plus) à la vitesse de la lumière, ce qu'avait déjà remarqué Henri Poincaré en en parlant d'une « onde gravifique »[1] - [2]. Albert Einstein prédit plus précisément l'existence d'ondes gravitationnelles en , en se fondant sur sa théorie de la relativité générale[3] - [4].
Cependant, la réalité des ondes gravitationnelles a été longuement débattue, Einstein changeant lui-même plusieurs fois d'avis à ce sujet[5] - [6] - [7]. La question était de savoir si ces ondes avaient effectivement une existence physique ou bien résultaient d'un « pur effet de jauge », autrement dit d'un choix de système de coordonnées. Cette question fut définitivement tranchée lors de la conférence de Chapel Hill (Caroline du Nord) (États-Unis) en 1957[8]. Les contributions de Felix Pirani et Hermann Bondi furent déterminantes. Pirani montra qu'en présence d'une onde gravitationnelle, un ensemble de masses en chute libre est animé d'un véritable mouvement les unes par rapport aux autres (tel qu'illustré plus haut). Bondi suggéra qu'en connectant deux masses aux extrémités d'un piston, on absorberait l'énergie de l'onde en la transformant en chaleur (« sticky bead » argument), ce qui démontre que l'onde doit posséder une réalité physique. Ce fut le point de départ du développement d'instruments permettant la mise en évidence expérimentale des ondes gravitationnelles.
Détections
L'observation du pulsar binaire PSR B1913+16[9] permit aux physiciens Russell Hulse et Joseph Taylor de disposer d’un indice sérieux en faveur de l'existence des ondes gravitationnelles, en montrant que la diminution de période de ce système binaire s'expliquait avec précision par l'émission de telles ondes[10]. Ce travail fut récompensé par le prix Nobel de physique en 1993[11].
Le , les chercheurs du LIGO annoncent avoir détecté directement des ondes gravitationnelles ; cette annonce est confirmée officiellement le [12] - [13], le résultat est publié le jour même dans la revue Physical Review Letters[14]. Ces ondes gravitationnelles ont été produites par la coalescence de deux trous noirs, situés à 1,3 milliard d'années-lumière[15]. Ce serait aussi « la première preuve directe de l’existence des trous noirs », affirme Thibault Damour, physicien théoricien français[16]. Le phénomène est observé une deuxième fois en décembre 2015 (annoncé en juin 2016), la détection ayant été à nouveau réalisée par l'expérience LIGO[17]. Ce nouveau signal est baptisé GW151226[18]. Le 3 octobre 2017, le prix Nobel de physique 2017 a été attribué conjointement à Rainer Weiss, Barry C. Barish et Kip Thorne pour récompenser leurs recherches sur les ondes gravitationnelles.
Le 17 août 2017, une contrepartie électromagnétique est captée après la détection d'un signal d'ondes gravitationnelles, permettant une étude fine de la source : une fusion d’étoiles à neutrons. Cette double détection est l'acte de naissance d'une nouvelle discipline, l'astronomie multimessager.
Le , la coopération LIGO/Virgo détecte la collision d'un trou noir et d'un objet de nature inconnue : avec une masse de 2,50 à 2,67 M⊙, il est en principe trop lourd pour une étoile à neutrons, mais trop léger pour un trou noir.
Phénomène physique
Dans la théorie de la relativité générale, la gravité provient de la courbure de l'espace-temps. Cette courbure est causée par la présence d'objets possédant une masse. Plus la masse de l'objet est grande, plus la courbure produite est grande et ainsi plus la gravité est intense. Lorsque des objets massifs se déplacent dans l'espace-temps, la courbure de l'espace-temps s'ajuste pour refléter le changement de la position de ces objets. Sous certaines circonstances, les objets accélérés peuvent produire une perturbation de l'espace-temps qui s'étend et se propage de manière analogue à « des vagues à la surface de l'eau ». On désigne par onde gravitationnelle[5] - [19] (ou parfois onde de gravitation[20] - [21] - [22]) ce type de perturbation, et on prédit qu'elles se propagent à la vitesse de la lumière. Ces ondes sont inexistantes dans la théorie newtonienne qui suppose une propagation instantanée de la gravitation.
L'analogie entre des charges électriques en mouvement et des masses en mouvement permet de mieux appréhender le phénomène : de la même manière que l'accélération de particules chargées produit des ondes électromagnétiques, l'accélération de particules possédant une masse produit des ondes gravitationnelles. La plupart des théories de gravité quantique postulent l'existence d'une particule élémentaire correspondante appelée le graviton[5], de façon analogue à l'électrodynamique quantique dans laquelle le vecteur de la force électromagnétique n'est autre que le photon. Le graviton est associé à l'onde gravitationnelle, les caractéristiques de cette dernière donnent de précieuses informations sur cette particule. Cependant, même après la mise en évidence des ondes gravitationnelles, l’existence du graviton reste hypothétique.
Les éventuels objets constitués de matière noire, ainsi que leurs événements de fusion, pourraient eux aussi émettre des ondes gravitationnelles détectables par les dispositifs LIGO[23]. En fait, de nombreux types d'événements astrophysiques pourraient en principe créer des ondes gravitationnelles, avec des fréquences allant de quelques kHz à quelques nHz. Dans la gamme de fréquences nHz les sources potentielles comprennent les cordes cosmiques, les fluctuations quantiques de l'Univers primordial et, notamment, les binaires de trous noirs supermassifs (SMBHB, pour supermassive black hole binary). Certaines sources d'ondes gravitationnelles sont si nombreuses qu'elles devraient contribuer à un fond d'ondes gravitationnelles (GWB, pour gravitational wave background). Ce fond est la cible des réseaux de synchronisation de pulsars (PTA, pour pulsar timing array) depuis des décennies, et pourrait être détecté prochainement[24].
Effet
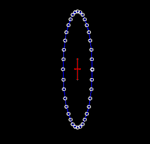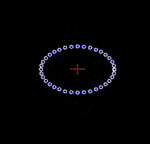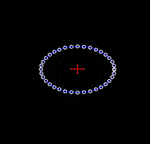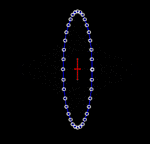 Déformation d'un anneau de particules au passage d'une onde gravitationnelle polarisée "+", dans le plan du front de l'onde. |
 Déformation d'un anneau de particules au passage d'une onde gravitationnelle polarisée "x", dans le plan du front de l'onde. |
On considère un cercle de particules test en chute libre (soumises uniquement à la gravité). Les ondes gravitationnelles étant « transverses », leur effet sur les particules est nul dans la direction de propagation. Par contre, une onde gravitationnelle qui se propage perpendiculairement au plan du cercle entraîne la déformation de ce cercle. Il est étiré de manière alternée dans une direction tandis qu'il est comprimé dans l'autre, tout en gardant une surface constante, comme indiqué dans les animations ci-contre. L'amplitude des oscillations montrées dans les animations est grandement exagérée. En réalité, l'amplitude des ondes gravitationnelles est très petite.
Les animations permettent de visualiser les oscillations associées à une onde gravitationnelle sinusoïdale, ce qui explique l'évolution des figures dans les animations. Une telle onde peut être produite par le système physique idéal constitué d'une paire de masses identiques en orbite circulaire. Dans ce cas, l'amplitude de l'onde est constante[Note 1] et son plan de polarisation tourne continûment à deux fois la fréquence orbitale.
On note usuellement l'amplitude des ondes gravitationnelles h, qui est un nombre sans dimension, quantifiant l'importance relative de la compression ou de l'étirement dans les animations. L'amplitude montrée ci-contre est d'environ h = 0,5 (soit 50 %). Dans la réalité, les ondes gravitationnelles reçues sur Terre sont imperceptibles: typiquement, on estime que h ≈ 10-20, c'est-à-dire qu'un cercle de la taille de la Terre subirait une déformation d'environ 10−13 m, soit mille fois plus petite qu'un atome.
Polarisation
Il existe deux polarisations, ce qui est équivalent à dire que les ondes gravitationnelles possèdent deux degrés de liberté indépendants notés et .
Les deux polarisations indépendantes d'une onde gravitationnelle, aux propriétés identiques à l'unique polarisation d'une onde lumineuse, ont un angle entre elles de 45 degrés. L'effet d'une onde rectilignement polarisée avec la polarisation « plus » est identique à celui avec la polarisation « croix » mais tourné de 45 degrés comme illustré dans les animations ci-dessus. La polarisation des ondes gravitationnelles résulte de la nature de leur source et le degré de polarisation dépend de l'orientation de la source par rapport à l'observateur. Les ondes gravitationnelles sont définies comme les perturbations de la métrique qui du point de vue des équations d'Einstein sont découplées des perturbations du tenseur énergie-impulsion. Les ondes gravitationnelles ont une symétrie tensorielle (mathématiquement, on parle de spin 2), par opposition aux perturbations de la matière qui ont soit une symétrie scalaire (spin 0), soit une symétrie vectorielle (spin 1, par exemple pour la lumière). Ceci est directement relié au nombre de polarisations.
Pour trouver l'origine de ce nombre, il faut considérer le tenseur métrique dans son ensemble, qui est décrit par une matrice symétrique contenant dix entrées indépendantes, et soustraire tout d'abord les degrés de liberté non-physiques associés à l'invariance de la théorie sous la symétrie de reparamétrisation de l'espace-temps. Ceux-ci sont au nombre de quatre. Il faut également soustraire les degrés de liberté qui sont couplés aux perturbations du tenseur énergie-impulsion. Il y a un tel degré scalaire et trois degrés vectoriels. Finalement, il ne reste donc que deux degrés de propagation physique[Note 2].
Sources
Amplitude des ondes gravitationnelles émises par un système physique
La formule du quadrupôle obtenue par Albert Einstein en 1916 permet de relier l'amplitude de l'onde émise par un système physique à la variation de son moment quadrupolaire :
Pour un système continu doté d'une densité volumique de masse , celui-ci est[25] où les indices correspondent aux coordonnées cartésiennes et est le symbole de Kronecker.
La petitesse du facteur traduit la grande rigidité de l'espace-temps. Il faut la compenser par de grandes variations du moment quadrupôlaire pour produire des ondes gravitationnelles détectables.
Ceci a plusieurs conséquences importantes. Les systèmes dont la dynamique est à symétrie sphérique (sphère en expansion ou en contraction) ou à symétrie cylindrique (disque en rotation sur son axe) n'émettent pas d'ondes gravitationnelles puisque leur moment quadrupolaire reste constant.
Un dispositif simple pour la production d'onde gravitationnelle est un haltère en rotation autour du centre de son axe. Un tel système avec deux masses m séparées d'une distance R en rotation à la vitesse angulaire donne . Cette estimation, appliquée à des systèmes aux dimensions réalistes pour une expérience construite par l'homme, montre que la production d'ondes gravitationnelles détectables est impraticable en laboratoire.
C'est pourquoi l'on s'intéresse à des sources astrophysiques, qui font généralement intervenir des objets compacts (comme les étoiles à neutrons et les trous noirs) présentant de grandes masses et capables de soutenir de très grandes accélérations.
Binaires compactes coalescentes

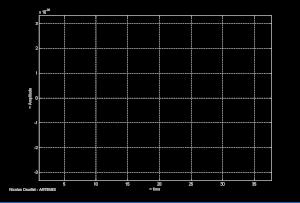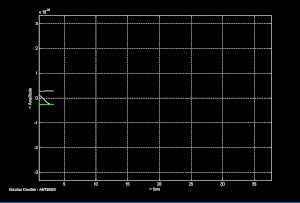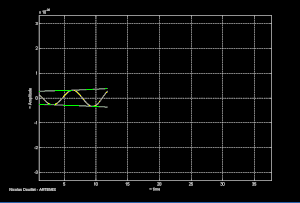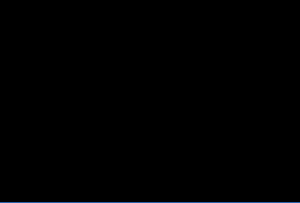
Les systèmes binaires d'étoiles à neutrons et/ou trous noirs proches de la coalescence sont l'équivalent astrophysique de l'haltère en rotation mentionné plus haut. Les deux objets composant le système orbitent l’un autour de l’autre. Le système perd de l'énergie par rayonnement gravitationnel ce qui cause le rapprochement des deux objets jusqu’à la coalescence. La fréquence orbitale augmente au fur et à mesure que le rayon orbital diminue. Ceci conduit à l'émission d'un signal gravitationnel caractéristique comme illustré ci-contre.
Fond stochastique
On distingue le fond stochastique d'onde gravitationnelle d’origine astrophysique dû à la superposition des signaux provenant d'un grand nombre de sources irrésolues (qu'il est impossible de détecter séparément) et celui d'origine cosmologique produit lors des premiers instants de l’Univers peu de temps après le Big Bang. L'observation de ce rayonnement donnerait des informations importantes sur l'Univers primordial, en particulier sur la période dite d'inflation cosmique[26].
Sources continues
Si elles possèdent un certain degré de non-axisymétrie, les étoiles à neutrons émettent une onde gravitationnelle monochromatique à la fréquence double de la fréquence de rotation de l’étoile. L'émission étant permanente, constante en fréquence et amplitude, on peut alors « intégrer » le signal pendant plusieurs mois afin de le distinguer du bruit instrumental.
Détecteurs
Barres résonnantes
Les barres de Weber sont des instruments simples permettant de détecter l'effet d'une onde gravitationnelle. Il s'agit d'une barre rigide de métal isolée des vibrations externes. La distorsion de l'espace causée par une onde gravitationnelle incidente excite la barre à sa fréquence de résonance, perturbation ensuite amplifiée jusqu'à des niveaux détectables. Ce type de détecteur a été proposé et utilisé initialement par Joseph Weber de l'université du Maryland. Weber a déclaré à plusieurs reprises avoir observé un excès de coïncidence entre les événements observés par deux barres identiques séparées de 2 km[27], ce qui l'a conduit à déclarer la découverte des ondes gravitationnelles en 1969[28]. Ce résultat n'a pas été confirmé par les expériences de validation conduites ultérieurement[29].
Le principe du détecteur de Weber a été développé par la suite par plusieurs équipes. La cryogénie a été introduite afin d'atteindre une meilleure sensibilité en atténuant le bruit thermique causé par l'agitation brownienne des atomes composant la barre. On dénombre plusieurs instruments de ce type dans le monde, dont certains sont encore en service : ALLEGRO (Bâton-Rouge, États-Unis, actuellement démantelé), AURIGA (Legnaro/Padoue, Italie), Explorer (CERN, Suisse) et NAUTILUS (Rome Frascati, Italie). La géométrie sphérique, plutôt que cylindrique généralement utilisée, a été proposée pour le projet de détecteur miniGrail (Pays-Bas).
Décroissance orbitale des pulsars binaires
L'observation du pulsar binaire PSR B1913+16, découvert en 1974, a permis aux physiciens Russell Hulse et Joseph Taylor de disposer d’un indice sérieux en faveur de l'existence des ondes gravitationnelles. Ce système binaire est composé de deux étoiles à neutrons. L'une au moins est un pulsar. Hulse et Taylor en ont observé les impulsions radio pendant plusieurs années et ont suivi l'évolution de ses paramètres orbitaux, notamment la période orbitale, de l’ordre de 8 heures. La courbe de réduction de la période en fonction du temps qu’ils ont mesurée montre que le système perd de l'énergie et que la réduction correspond avec une extrême précision, dans le cas d’une perte d’énergie par rayonnement gravitationnel, à celle que prévoit la relativité générale[30] :
- Décroissance de la période orbitale régie par l’équation .
- Précision des mesures : période orbitale à près. Valeur jours. Autre paramètre : excentricité de l’orbite à près : , etc.
Le modèle indique que la coalescence des deux étoiles devrait se produire dans 300 millions d’années. Russell Hulse et Joseph Taylor furent récompensés par le prix Nobel de physique en 1993 pour cette découverte.
Polarisation et mode B du fond diffus cosmologique
En mars 2014, des chercheurs du Centre d'astrophysique Harvard-Smithsonian annoncent la détection des ondes gravitationnelles produites lors de l'inflation cosmique grâce à la mesure de la polarisation du fond diffus cosmologique par le télescope BICEP2 (Background Imaging of Cosmic Extragalactic Polarization)[31] - [32] - [33] - [34] - [35] - [36]. Cette étude est toutefois remise en cause plusieurs mois plus tard[37]. En effet, une analyse des données de BICEP2/Keck Array et du satellite Planck[38] qui utilise un modèle amélioré des émissions de la poussière galactique fournit une nouvelle limite supérieure sur la contribution à la polarisation du fond diffus cosmologique due aux ondes gravitationnelles primordiales. La conclusion est qu'il n'est plus exclu que cette contribution soit nulle (et que la polarisation observée soit presque intégralement due à la poussière galactique et aux effets de lentille gravitationnelle).
Détecteurs interférométriques terrestres
.svg.png.webp)

La première génération de détecteurs interférométriques d'ondes gravitationnelles comprend six instruments de grandes dimensions. Le projet américain LIGO consiste en trois instruments kilométriques situés au complexe nucléaire de Hanford WA (ce site accueille deux interféromètres dans la même enceinte) et Livingston LA[39]. Le projet franco-italien Virgo situé à Cascina près de Pise (Italie) possède un instrument de même classe. Le projet germano-britannique GEO600 localisé à Hanovre (Allemagne) aux dimensions plus modestes (300 mètres) vient compléter cet ensemble. Le projet japonais TAMA de taille similaire à GEO est actuellement démantelé. Malgré des différences technologiques importantes, tous ces instruments suivent le même principe[Note 3]. Tous captent la distorsion de l'espace-temps qu'exerce une onde gravitationnelle en mesurant avec une grande précision la différence de longueur du chemin optique suivi par deux faisceaux laser se propageant dans deux directions orthogonales. En pratique on utilise l'interférométrie pour réaliser cette mesure comme indiqué sur le schéma ci-contre. Observer une variation de la différence de longueur revient à observer une variation de la différence de phase entre les deux faisceaux, donc une variation de leur figure d'interférence.

Le bruit de mesure (principalement le bruit thermique causé par l'agitation brownienne des atomes constituant les optiques et le bruit de photons dû à la nature quantique de la lumière) peut être réduit pour atteindre la précision de (cela correspond à l'épaisseur d'un cheveu sur la distance des étoiles proches), où représente l'amplitude de l'onde gravitationnelle, la longueur de chaque bras de l'interféromètre[40] (égale à plusieurs kilomètres), et le défaut de frange de l’ordre de mètres (soit mille fois inférieur à la taille du proton, 10−15 m)[41].
Une seconde génération de détecteurs avancés, dix fois plus sensible, a permis la première détection d'une onde gravitationnelle le par les Ligo de Livingston et de Hanford encore en phase de tests. Cette onde a été générée par la coalescence de deux trous noirs (respectivement de 29 et 36 fois la masse du soleil) il y a 1,3 milliard d'années. Une seconde détection de signal a été effectuée fin 2015. En Europe, l'interféromètre Virgo est entré en fonction en 2017.
En 2023, après trois ans de développements technologiques destinés à en augmenter la sensibilité, les détecteurs Ligo et Virgo, rejoints par le détecteur japonais Kagra, entament une nouvelle campagne d'écoute du cosmos, dénommée O4. Cette coopération internationale espère détecter plusieurs fusions de systèmes binaires par semaine, et aussi observer des événements moins puissants comme l'effondrement en supernova d'une étoile massive, voire l'émission continue d'ondes gravitationnelles par les pulsars[42].
Interféromètres spatiaux

Un moyen de s'affranchir du bruit sismique (terrestre) est de réaliser l'expérience dans l'espace. C'est l'objectif de la mission spatiale eLISA constituée de trois satellites en formation qui réalise dans l'espace un interféromètre à deux bras de près d'un million de kilomètres. (Initialement, il était prévu trois bras de cinq millions de kilomètres avant que la NASA abandonne la direction du projet LISA. C'est alors que l'Agence spatiale européenne (ESA) a pris la tête du projet et que celui-ci fut rebaptisé eLISA.) Le 28 novembre 2013, l'ESA a annoncé que la recherche des ondes gravitationnelles serait la thématique principale de la mission L3[43] avec un lancement prévu en 2034. Les technologies clefs d'eLISA ont été validées par le succès des tests réalisés avec le démonstrateur LISA Pathfinder (LPF)[44] - [45] lancé le 3 décembre 2015.
Perspectives
Si l’on tient compte du fait que les ondes gravitationnelles ne sont pas arrêtées par la matière comme le sont les ondes électromagnétiques, les astrophysiciens disposent désormais avec elles d’un champ nouveau d’observation qui leur permettra de « voir » certains aspects de l’univers à grande échelle, et notamment de se rapprocher de ses débuts, jusqu’alors inaccessibles, allant du big bang à 380 000 ans.
L'observation des ondes gravitationnelles signe aussi le succès des détecteurs interférométriques et leur capacité à détecter d'infimes variations de distance : lors du passage de l'onde gravitationnelle de GW150914, les miroirs des cavités des interféromètres de LIGO ont subi un déplacement maximal de m, un millier de fois inférieur à la taille du proton.
En revanche, l'existence des ondes gravitationnelles laisse ouverte la question de l’existence du graviton, une particule élémentaire dont certaines théories spéculatives de gravité quantique impliquent l’existence en association avec la gravitation (à l’instar du photon associé à l’électromagnétisme) : cette particule reste hypothétique.
Nomenclature
Les signaux significatifs détectés par la collaboration LIGO-Virgo sont classés en deux catégories. Les signaux les plus significatifs sont effectivement nommés « onde gravitationnelle » et reçoivent comme désignation les deux lettres « GW » (initiales de l'anglais gravitational wave) suivies de la date de détection dans le format AAMMJJ, où AA sont les deux derniers chiffres de l'année (par exemple 15 pour 2015), MM est le numéro du mois (par exemple 09 pour septembre) et JJ est le jour du mois. La première onde gravitationnelle détectée par LIGO, reçue le 14 septembre 2015, fut ainsi baptisée GW150914. À l'origine, les signaux moins significatifs, mais néanmoins suffisamment distincts du bruit de fond, sont classés comme « candidats ». Les signaux candidats reçoivent ainsi un nom composé des trois lettres « LVT » (signifiant LIGO-Virgo Trigger) suivies de la date de détection dans le même format que précédemment. Un tel exemple est LVT151012, signal détecté le 12 octobre 2015 ayant une relativement faible probabilité d'être une fausse alarme (environ 2 %) mais pas suffisamment faible pour être considéré de façon confiante comme une véritable onde gravitationnelle, et donc recevoir une désignation commençant par « GW ». Puis, à partir de novembre 2018, la dénomination « LVT » est abandonnée : « GW » est adopté pour tout nom de signal détecté significatif ou candidat. LVT151012 est ainsi renommé en GW151012[46] - [47].
Lors du troisième run d'observation du réseau, les « superévénements », événements détectés par plusieurs pipelines, reçoivent une désignation de la forme « SAAMMJJx », où AAMMJJ est la date de détection (les deux derniers chiffres de l'année, le numéro du mois sur deux chiffres et le jour du mois aussi sur deux chiffres) et « x » est une ou plusieurs lettres minuscules (a-z, puis aa-az, ba-bz, ..., za-zz, ...) attribuées de façon analogue aux supernovas (à la différence que, pour les supernovas, les lettres simples sont en majuscule, A-Z, et seules les lettres multiples sont en minuscules, aa-zz, aaa-zzz, ...). Ainsi, le quarantième superévénement du 8 avril 2019 a la désignation S190408an. La majorité de ces superévénements ne sont pas des vrais signaux astrophysiques ; seuls les plus significatifs sont effectivement considérés comme candidats.
Notes et références
Notes
- À échelle perceptible.
- À titre indicatif, la généralisation en dimension N de ce résultat aboutit à un nombre N (N -3)/ 2 de degrés de liberté pour les ondes gravitationnelles. Les ondes gravitationnelles dans des espaces à dimensions supplémentaires sont utiles dans le cadre de la cosmologie branaire.
- Idée suggérée pour la première fois dans M. E. Gertsenshtein et V. I. Pustovoit, JETP 43, 603 (1962) et dont l'applicabilité a été démontrée par R. Weiss, Electromagnetically Coupled Broadband Gravitational Antenna, Quarterly Progress Report, Research Laboratory of Electronics, MIT 105: 54 (1972).
Références
- « J'ai d'abord été conduit à supposer que la propagation de la gravitation n'est pas instantanée, mais se fait avec la vitesse de la lumière […] Quand nous parlerons donc de la position ou de la vitesse du corps attirant, il s’agira de cette position ou de cette vitesse à l’instant où l’onde gravifique est partie de ce corps ; quand nous parlerons de la position ou de la vitesse du corps attiré, il s’agira de cette position ou de cette vitesse à l’instant où ce corps attiré a été atteint par l’onde gravifique émanée de l’autre corps ; il est clair que le premier instant est antérieur au second » H. Poincaré, Sur la dynamique de l'électron, Comptes rendus de l'Académie des Sciences, t. 140, p. 1507 (5 juin 1905) ; texte sur wikisource.
- Jean Eisenstaedt, Einstein et la relativité générale, France Paris, CNRS Éditions, , 345 p. (ISBN 978-2-271-06535-3), chap. 2 (« Lumière et structure de l'espace-temps »). — Préface de Thibault Damour.
- (de) Albert Einstein, « Näherungsweise Integration der Feldgleichungen der Gravitation », Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (Berlin), vol. part 1, , p. 688-696 (Bibcode 1916SPAW.......688E, lire en ligne [PDF], consulté le ).
- (de) Albert Einstein, « Über Gravitationswellen », Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (Berlin), vol. part 1, , p. 154-167 (Bibcode 1918SPAW.......154E, lire en ligne [PDF], consulté le ).
- Entrée « onde gravitationnelle », dans Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Bruxelles, De Boeck Supérieur, 2e éd. (1re éd. ), XII-741 p., 24 cm (ISBN 978-2-8041-0248-7 et 2-8041-0248-3, OCLC 632092205, BNF 42122945), p. 389 [lire en ligne (page consultée le 16 février 2016)].
- (en) D. Kennefick, Traveling at the Speed of Thought: Einstein and the Quest for Gravitational Waves, Princeton University Press (2007).
- (en) M. Mitchell Waldrop, « The hundred-year quest for gravitationnal waves — in pictures », Nature, , News (DOI 10.1038/nature.2016.19340).
- (en) P. Saulson, A history of Gravitational Waves [PDF], inspiré par Josh Goldberg (2012), lire en ligne.
- (en) Russell A. Hulse et Joseph H. Taylor, « Discovery of a pulsar in a binary system » [« Découverte d'un pulsar dans un système binaire »], The Astrophysical Journal, vol. 195, , part. 2, p. L51-L53 (ISSN 0004-637X, DOI 10.1086/181708, Bibcode 1975ApJ...195L..51H, résumé, lire en ligne [PDF], consulté le ).
- (en) Joseph H. Taylor et Joel M. Weisberg, « A new test of general relativity: gravitational radiation and the binary pulsar PSR 1913+16 » [« Un nouveau test de la relativité générale : rayonnement gravitationnel et pulsar binaire PSR 1913+16 »], The Astrophysical Journal, vol. 253, , part. 1, p. 908-920 (ISSN 0004-637X, DOI 10.1086/159690, Bibcode 1982ApJ...253..908T, résumé, lire en ligne [PDF], consulté le ).
- (en) « The Nobel prize in physics 1993 » [« Le prix Nobel de physique 1993 »] [html], sur nobelprize.org (consulté le ).
- (en) « Viewpoint: The First Sounds of Merging Black Holes », sur physics.aps.org.
- AFP, « Des physiciens annoncent avoir détecté les ondes gravitationnelles d'Einstein », sur lepoint.fr, .
- (en) Abbott et al., « Observation of Gravitational Waves from a Binary Black Hole Merger », Physical Review Letters, American Physical Society, vol. 116, no 061102, (lire en ligne).
- (en) « Einstein's gravitational waves found at last », sur nature.com.
- Thibault Damour, interview par Hervé Morin, Le plus important, c'est la preuve de l'existence de trous noirs, lemonde.fr, (consulté le ).
- LEXPRESS.fr avec AFP, « Deuxième détection directe des ondes gravitationnelles d'Einstein », l'Express, (lire en ligne, consulté le )
- (en) B. P. Abbott et al., « GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence », Physical Review Letters, (DOI 10.1103/PhysRevLett.116.241103)
- (en) Entrée « gravitational wave » [« ondes gravitationnelles »] [php] dans Mohammad Heydari-Malayeri, An etymological dictionary of astronomy and astrophysics : english-french-persian [« Un dictionnaire étymologique d'astronomie et d'astrophysique: anglais-français-persan »], Paris, Observatoire de Paris, -.
- Michel Biezunski, Histoire de la physique moderne (monographie), Paris, La Découverte, coll. « Histoire des sciences », 1re éd., 239 p., 22 cm (ISBN 2-7071-2254-8 et 978-2-7071-2254-4, OCLC 299550504, BNF 35600028, présentation en ligne), chap. 7 (« L'unité retrouvée (1965-1990) »), § [8] (« Ondes gravitationnelles »), p. 127 [lire en ligne (page consultée le 16 février 2016)].
- Pierre Léna, Daniel Rouan, François Lebrun, François Mignard et Didier Pelat (avec la collaboration de Laurent Mugnier), L'observation en astrophysique (monographie), Les Ulis et Paris, EDP Sciences / CNRS Éditions, coll. « Savoirs actuels / Astrophysique », 3e éd., XIII-742-[16], 23 cm (ISBN 978-2-86883-877-3, 2-86883-877-4, 2-271-06744-8 et 978-2-271-06744-9, OCLC 244475319, BNF 41287342, présentation en ligne), chap. 1 (« L'information en astrophysique »), sect. 1.1 (« Les porteurs de l'information »), § 1.1.4 (« Les ondes gravitationnelles »), p. 8 [lire en ligne (page consultée le 16 février 2016)].
- Jean-Pierre Luminet et Élisa Brune, Bonnes nouvelles des étoiles (monographie), Paris, Odile Jacob, coll. « Sciences », , 332 p., 22 cm (ISBN 978-2-7381-2287-2 et 2-7381-2287-6, OCLC 470972888, BNF 41479909, présentation en ligne), « Les ondes gravitationnelles », p. 166 [lire en ligne (page consultée le 16 février 2016)].
- (en) C. Sivaram et Kenath Arun, « Dark Matter Objects: Possible New Source of Gravitational Waves », Earth, Moon, and Planets (en), vol. 123, nos 1-2, , p. 9-13 (DOI 10.1007/s11038-019-09527-2).
- (en) Chiara M. F. Mingarelli et J. Andrew Casey-Clyde, « Seeing the gravitational wave universe », Science, vol. 378, no 6620, , p. 592-593 (DOI 10.1126/science.abq1187
 ).
). - Eric Weisstein, « Electric Quadrupole Moment », Eric Weisstein's World of Physics, Wolfram Research (consulté le ).
- (en) S. Kuroyanagi et al., Prospects for determination of thermal history after inflation with future gravitational wave detectors, Phys. Rev. D 84:123513 (2011), lire en ligne.
- J. Weber, Gravitational-Wave-Detector Events, Phys. Rev. Lett. 20, 1307–1308 (1968), lire en ligne.
- (en) J. Weber, Evidence for Discovery of Gravitational Radiation, Phys. Rev. Lett. 22, 1320–1324 (1969), lire en ligne.
- (en) H. Billing, P. Kafka, K. Maischberger, F. Meyer et W. Winkler, Results of the Munich-Frascati gravitational-wave experiment, Lettere Al Nuovo Cimento vol. 12, no 4, p. 111-116, 1975, lire en ligne.
- Source : cours de Françoise Combes.
- (en) Ron Cowen, « Telescope captures view of gravitational waves », Nature, .
- « Big Bang : les ondes gravitationnelles d'Einstein enfin détectées ».
- (en) Article plus détaillé sur BBC News.
- « Inflation : les ondes gravitationnelles du Big Bang enfin découvertes ? », sur futura-sciences.com.
- « Ondes gravitationnelles primordiales : la preuve décisive de l'inflation cosmique se rapproche », sur pourlascience.fr.
- « Découverte majeure en astrophysique : les ondes gravitationnelles issues du Big Bang enfin détectées », émission de France Inter La Tête au carré du 28 mars 2014.
- (en) « Gravitational waves turn to dust after claims of flawed analysis », The Guardian.
- A Joint Analysis of BICEP2/Keck Array and Planck Data.
- (en) Martin Hendry, « Gravitional Astronomy : opening a new window on the cosmos », Electro Optics, vol. 267, , p. 12 (ISSN 0013-4589)
- article du Monde du 11 février
- Voir cours de Françoise Combes.
- Marie-Anne Bizouard et Sean Bailly, « Ligo et Virgo : une nouvelle campagne d'écoute du cosmos », Pour la science, no 549, , p. 7.
- Mission L3, sur elisascience.org.
- (en) Patric Blau, « LISA Pathfinder Spacecraft ends Communications with Earth after superb Mission Success », sur Spaceflight101,
- (en) « LISA Pathfinder to conclude trailblazing mission », ESA,
- (en) « LIGO Scientific Collaboration - The science of LSC research », sur ligo.org (consulté le ).
- (en) The LIGO Scientific Collaboration et the Virgo Collaboration, « GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs », (consulté le ).
Voir aussi
Bibliographie
- Pierre Binétruy, À la poursuite des ondes gravitationnelles, Dunod, coll. « Quai des Sciences », , 256 p. (ISBN 978-2100721856, BNF 44369000).
- [Blanchet 2017] Luc Blanchet, « Les ondes gravitationnelles, cent ans après Einstein », Reflets de la physique, no 52, , p. 6-12 (DOI 10.1051/refdp/201752006, résumé, lire en ligne [PDF]).
- (en) Michele Maggiore, Gravitational Waves: Volume 1: Theory and Experiments, Oxford Univ. Press, 2007.
- Matteo Barsuglia, Les vagues de l'espace-temps : la révolution des ondes gravitationnelles, Dunod, coll. « Quai des Sciences », , 208 p. (ISBN 978-2100781591).
- Philippe Tourrenc, Relativité et gravitation, Armand Colin, 1997.
- Nathalie Deruelle et Jean-Pierre Lasota, Les Ondes gravitationnelles, Odile Jacob, 2018, (ISBN 978-2-7381-4334-1)
- (de) Albert Einstein, « Näherungsweise Integration der Feldgleichungen der Gravitation », article original,
Articles connexes
- DECIGO (en), projet japonais pour tenter de détecter les ondes gravitationnelles
- Liste d'ondes gravitationnelles
Liens externes
- « Ondes gravitationnelles : la déferlante », La Méthode scientifique, France Culture, 30 novembre 2021.
- Françoise Combes, Diagnostics observationnels, perspectives, cours dispensé au Collège de France le , dans le cadre de la chaire « Galaxies et cosmologie » dont elle est titulaire, année 2015-2016 « Trous noirs super-massifs, noyaux actifs et quasars » : cours accessible sur le site du Collège de France.
- (en) « Fifty Gravitational Wave Events Illustrated », sur Astronomy Picture of the Day, NASA, (consulté le ) (traduction/adaptation française)
- Notices dans des dictionnaires ou encyclopédies généralistes :























