Détermination d'une structure cristalline

La détermination d'une structure cristalline consiste, de manière générale, à déterminer, pour un cristal de structure inconnue, les paramètres de sa maille conventionnelle, son réseau de Bravais, son groupe d'espace et la position des atomes dans la maille. Dans la pratique, on utilise des méthodes de radiocristallographie, comme la diffraction de rayons X, la diffraction de neutrons ou la diffraction des électrons, pour la détermination de structure. Le plus souvent, les structures cristallines sont déterminées à partir d'échantillons monocristallins, mais cela est aussi possible en utilisant des poudres.

Le problème central de la détermination d'une structure cristalline est l'absence d'information sur la phase des facteurs de structure lors d'une mesure de diffraction. Plusieurs méthodes ont été développées pour résoudre ce « problème de phase » dans le cas de la diffraction par des rayons X : méthodes directes, méthode de Patterson, méthode de l'atome lourd, remplacement isomorphe, remplacement moléculaire, diffraction anomale, recuit simulé, méthode d'entropie maximum, charge flipping, fonction de distribution de paires, mesure expérimentale de phases.

Des méthodes complémentaires comme la spectrométrie d'absorption des rayons X ou la spectroscopie Mössbauer donnent aussi des informations sur la composition du cristal, le degré d'oxydation et l'environnement des espèces chimiques.

Historique

La première structure cristalline déterminée par diffraction de rayons X avec une résolution atomique fut celle du chlorure de sodium NaCl[1] - [2] - [3].

En 1985, Herbert Aaron Hauptman et Jerome Karle obtinrent le prix Nobel de chimie pour « leurs réalisations remarquables dans la mise au point de méthodes directes de détermination des structures cristallines[4] ».

Problème de phase

Le problème de phase vient du fait qu'une grande partie de l'information sur la structure d'un cristal, contenue dans la phase de l'onde diffractée, n'est pas accessible expérimentalement.

Lors d'une expérience de diffraction sur un cristal, la taille du faisceau incident est beaucoup plus grande que le cristal, afin d'assurer une diffraction homogène dans tout le cristal. On peut alors considérer que l'onde incidente $\psi \,$ , de longueur d'onde λ, a la forme d'une onde plane, décrite en tout point ${\vec {x}}$ et à chaque instant t par l'expression complexe :

\psi ({\vec {x}},t)=\psi _{0}\mathrm {e} ^{i\left(\omega t-2\pi {\vec {k}}\cdot {\vec {x}}+\varphi _{0}\right)}

où $\psi _{0}\,$ est l'amplitude de l'onde, $\omega \,$ sa pulsation, ${\vec {k}}$ son vecteur d'onde et $\varphi _{0}\,$ sa phase au temps t=0, que l'on choisit généralement nulle.

L'onde diffractée $\psi ''\,$ par un cristal est alors donnée par :

\psi ''({\vec {x}},t)=\psi _{0}\mathrm {e} ^{i(2\pi {\vec {k}}'\cdot {\vec {x}}-\omega t)}\cdot S_{\vec {K}}\cdot F({\vec {K}})=\psi _{0}\mathrm {e} ^{i(2\pi {\vec {k}}'\cdot {\vec {x}}-\omega t)}\cdot S_{\vec {K}}\cdot \sum _{j=1}^{n}f_{j}\mathrm {e} ^{2i\pi \cdot {\vec {K}}\cdot {\vec {r}}_{j}}

avec ${\vec {k}}'$ le vecteur d'onde de l'onde diffractée, ${\vec {K}}={\vec {k}}'-{\vec {k}}$ le vecteur de diffusion (variable continue), $S_{\vec {K}}$ le facteur de forme du cristal et $F({\vec {K}})$ le facteur de structure, contenant dans sa phase l'information sur la structure de la maille : ${\vec {r}}_{j}$ est le vecteur position et $f_{j}$ le facteur de diffusion atomique de l'atome $j$ dans la maille.

Le facteur de structure d'un cristal s'annule pour des vecteurs de diffusion ne satisfaisant pas la condition de Laue. L'ensemble des vecteurs de diffraction est un sous-ensemble discret de celui des vecteurs de diffusion pour lequel une intensité diffractée peut être observée (elle peut cependant être nulle pour certains vecteurs de diffraction si le groupe d'espace du cristal conduit à des extinctions systématiques). Par la suite ne seront considérés que les vecteurs de diffraction, notés ${\vec {H}}$ :

F({\vec {H}})=\sum _{j=1}^{n}f_{j}\mathrm {e} ^{2i\pi \cdot {\vec {H}}\cdot {\vec {r}}_{j}}=|F({\vec {H}})|\mathrm {e} ^{i\varphi ({\vec {H}})}=\int _{x=0}^{1}\int _{y=0}^{1}\int _{z=0}^{1}\rho (x,y,z)\mathrm {e} ^{2i\pi (hx+ky+lz)}\mathrm {d} x\mathrm {d} y\mathrm {d} z

où $\rho$ est la densité électronique de la maille.

L'onde diffractée est proportionnelle à la transformée de Fourier de la maille : en effectuant la transformée de Fourier inverse de l'onde diffractée, il devrait être possible de déterminer la structure de la maille. Cependant, la quantité accessible expérimentellement est l'intensité I, proportionnelle au carré de la norme de l'onde diffractée :

I(hkl)\propto |\psi ''({\vec {x}},t)|^{2}\propto |F({\vec {H}})|^{2}

avec h, k et l les coordonnées dans l'espace réciproque du point où l'intensité est mesurée, soit les composantes du vecteur de diffraction ${\vec {H}}$ .

L'intensité d'une réflexion est une quantité réelle, ne contenant pas d'information sur la phase $\varphi$ de l'onde diffractée : il n'est pas possible de déterminer directement la structure du cristal en effectuant une transformée de Fourier inverse de l'intensité mesurée. C'est le problème de phase de la cristallographie.

Méthodes de solution du problème de phase

Les méthodes ci-dessous ont été développées afin de résoudre le problème de phase, c'est-à-dire d'assigner la phase correcte à chaque facteur de structure. Beaucoup d'entre elles utilisent une ou plusieurs hypothèses de base qui découlent des propriétés de la distribution de la densité électronique $\rho ({\vec {r}})$ dans un cristal :

la densité électronique est en tout point positive (ou éventuellement nulle) ;
la densité électronique possède plusieurs maxima relativement bien localisés (autour des atomes).

De par la nature de ces hypothèses, on comprend que les méthodes de solution du problème de phase ne peuvent être appliquées qu'à des données de diffraction de rayons X : en effet, les interactions des rayons X avec la matière s'effectuent avec les électrons. Dans le cas de la diffraction de neutrons, les longueurs de diffusion atomiques peuvent être négatives, ce qui détruit les hypothèses ci-dessus.

Méthodes directes

Les méthodes directes utilisent des conditions sur la densité électronique dans un cristal afin d'établir des relations entre les phases des facteurs de structure. Elles se basent sur les travaux de Harker et Kasper[5], Karle et Hauptmann[6] - [7] et Sayre[8], entre autres.

Les méthodes directes nécessitent une connaissance (au moins approximative) de la composition chimique du cristal, du nombre de chaque espèce chimique dans la maille et du groupe d'espace du cristal. En plus des deux hypothèses sur la densité électronique, elles ne considèrent que les cas où tous les atomes ont un facteur de diffusion comparable (par exemple, C, N, O comme dans les composés organiques).

Ces méthodes utilisent plusieurs outils mathématiques :

des tests statistiques sur la valeur absolue des facteurs de structure pour déterminer la centrosymétrie d'un cristal ;
les inégalités d'Harker-Kasper qui donnent des relations entre les phases de différents facteurs de structure en fonction des opérations de symétrie du groupe d'espace ;
l'équation de Sayre, basée sur le théorème de convolution, qui permet de calculer directement la phase d'un facteur de structure appartenant à un « triplet » de réflexions.

La plupart des structures organiques ont été déterminées par des méthodes directes.

Méthode de Patterson

La méthode de Patterson utilise les propriétés des séries de Fourier dont les coefficients sont les produits des facteurs de structure avec leurs conjugués, $|F({\vec {H}})\cdot F^{*}({\vec {H}})|$ , afin de déterminer les vecteurs entre atomes dans un cristal. Elle n'utilise que les intensités mesurées et ne prend pas en compte les phases des facteurs de structure. Cette méthode a été développée par A.L. Patterson en 1934[9]. Elle utilise plus précisément le théorème de convolution : la transformée de Fourier inverse du produit des facteurs de structure avec leurs conjugués est égale à la fonction d'autocorrélation de la densité électronique, aussi appelée fonction de Patterson :

\rho ({\vec {r}})*\rho (-{\vec {r}})=\int _{-\infty }^{+\infty }|F({\vec {H}})\cdot F^{*}({\vec {H}})|\mathrm {e} ^{2i\pi ({\vec {H}}\cdot {\vec {r}})}{\mbox{d}}{\vec {H}}

La fonction de Patterson, calculée dans l'espace direct, est constituée de maxima qui correspondent aux vecteurs entre atomes dans la structure, centrés à l'origine de la maille. Ces vecteurs sont pondérés : d'après l'expression de la fonction de Patterson, chaque maximum est obtenu par convolution des densités électroniques individuelles de deux atomes et sa valeur dépend du nombre d'électrons des atomes. Les contributions des atomes lourds (à grand numéro atomique relativement aux autres atomes du cristal) sont donc particulièrement visibles.

Méthode de l'atome lourd

Principe de la méthode de l'atome lourd. Le facteur de structure F(hkl) est représenté en rouge, celui de l'atome lourd, F_HA(hkl), est en bleu. Les contributions des atomes légers sont en noir.

Carte de différence Fourier F'-F_HA après localisation de l'atome lourd. Les pics restants permettent de retrouver les atomes légers.

La présence d'un atome lourd (noté HA) dans la structure facilite la détermination de structure, car cet atome peut être localisé facilement dans la maille à partir de la méthode de Patterson. Son facteur de structure partiel F_HA peut alors être calculé :

F_{HA}({\vec {H}})=\sum _{p=1}^{n}f_{HA}\mathrm {e} ^{2i\pi \cdot {\vec {H}}\cdot {\vec {r}}_{HA,p}}=|F_{HA}({\vec {H}})|\mathrm {e} ^{i\varphi _{HA}({\vec {H}})}

où la somme sur $p$ prend en compte l'ensemble des atomes équivalents par symétrie dans la maille.

La méthode de l'atome lourd consiste à remplacer la phase du facteur de structure total par celle du facteur de structure partiel de l'atome lourd, puisqu'il contribue majoritairement aux intensités observées :

F({\vec {H}})=|F({\vec {H}})|\mathrm {e} ^{i\varphi ({\vec {H}})}\approx F'({\vec {H}})=|F({\vec {H}})|\mathrm {e} ^{i\varphi _{HA}({\vec {H}})}

Les atomes plus légers sont localisés par une analyse de différence Fourier, la densité électronique différence $\Delta \rho$ calculée par la transformée de Fourier inverse de la différence F'-F_HA permet de mieux mettre en évidence leurs positions :

\Delta \rho ({\vec {r}})={\frac {1}{V}}\sum _{\vec {H}}\left[F'({\vec {H}})-F_{HA}({\vec {H}})\right]\mathrm {e} ^{2i\pi {\vec {H}}\cdot {\vec {r}}}

où $V$ est le volume de la maille.

L'utilisation des atomes lourds dans la détermination d'une structure cristalline a été introduite par David Harker en 1936[10].

Remplacement isomorphe

La méthode du remplacement isomorphe est utilisée lorsqu'il est possible de substituer une espèce chimique A par une autre espèce B de numéro atomique différent dans la structure, sans que celle-ci ne change de symétrie. Les deux cristaux, l'un contenant A et l'autre contenant B, sont mesurés par diffraction. L'atome B est généralement choisi plus lourd que l'atome A : sa position peut être déterminée par la méthode de Patterson et la phase de son facteur de structure partiel pour une réflexion donnée est alors connue. La différence entre les deux jeux de données provient de la substitution atomique, ce qui permet de retrouver la position des atomes substitués. Il s'agit d'une des plus anciennes méthodes de détermination de structure, inventée par J.M. Cork en 1927 pour déterminer la structure des aluns[11].

La position des atomes A et B étant connue, le facteur de structure total pour une réflexion donnée peut être séparé en une somme de facteurs de structure partiels pour les cristaux 1 (contenant A) et 2 (contenant B) :

{\begin{array}{l}F_{1}({\vec {H}})=F_{1,A}({\vec {H}})+F_{1,X}({\vec {H}})\\[1ex]F_{2}({\vec {H}})=F_{2,B}({\vec {H}})+F_{2,X}({\vec {H}})\\[1ex]\end{array}}

Principe du remplacement isomorphe.

où F_X représente la contribution des autres atomes non substitués dans la maille au facteur de structure, d'où :

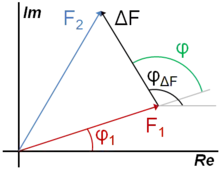
\Delta F({\vec {H}})=F_{2}({\vec {H}})-F_{1}({\vec {H}})=F_{2,B}({\vec {H}})-F_{1,A}({\vec {H}})

En effet, puisque les atomes non substitués lors du remplacement isomorphe occupent les mêmes positions dans les deux structures, leurs contributions aux facteurs de structure sont égales. La phase du facteur de structure total pour le cristal 1 peut alors se déduire par la relation (voir figure à droite)[12] :

{\begin{array}{rcl}\varphi _{1}({\vec {H}})&=&\displaystyle {\varphi _{\Delta F}({\vec {H}})-\cos ^{-1}\left[{\frac {|F_{2}({\vec {H}})|^{2}-|F_{1}({\vec {H}})|^{1}-|\Delta F({\vec {H}})|^{2}}{2|F_{1}({\vec {H}})||\Delta F({\vec {H}})|}}\right]}\\[3ex]&=&\varphi _{\Delta F}({\vec {H}})\pm \varphi ({\vec {H}})\end{array}}

La valeur absolue de $\varphi$ peut être calculée, mais son signe n'est pas connu si seulement deux cristaux isomorphes sont utilisés. Les deux possibilités sont donc testées par une analyse de différence Fourier[13].

La méthode du remplacement isomorphe n'est plus vraiment utilisée pour les cristaux inorganiques à cause du succès des méthodes directes ou de Patterson ; cependant, elle est très utile dans le cas des structures de macromolécules biologiques[14].

Remplacement moléculaire

Lorsqu'un cristal inconnu contient un fragment moléculaire connu, dont la structure a été déterminée dans un autre composé cristallin, il est possible de retrouver la position et l'orientation du fragment dans le cristal inconnu en comparant les fonctions de Patterson des deux cristaux : du fait de la présence du fragment dans les deux structures, les fonctions de Patterson présentent des caractéristiques similaires[15]. Lorsque la position et l'orientation du fragment ont été trouvées, le reste de la structure peut être déterminé par une succession d'affinements et analyses de la densité électronique à partir des cartes de différence Fourier.

L'utilisation de la méthode du remplacement moléculaire suppose l'existence d'une banque de données des structures déjà déterminées, contenant le même fragment que le cristal inconnu. Il s'agit d'une méthode importante pour les structures de macromolécules biologiques[16].

Diffraction anomale

La méthode de la diffraction anomale à plusieurs longueurs d'onde (MAD, Multi-wavelength anomalous diffraction) est une méthode de solution du problème de phase. Il s'agit d'une technique de diffraction de rayons X, surtout accessible en synchrotron : elle consiste en une série d'expériences de diffraction avec des longueurs d'onde différentes afin d'utiliser les effets de la diffusion anomale. L'importance de la diffusion anomale pour la résolution de structures a été remarquée dès 1949 par Johannes Martin Bijvoet, qui a utilisé la violation de la loi de Friedel afin de déterminer la configuration absolue de molécules[17] - [18].

La diffraction anomale est employée pour déterminer la structure de protéines[19] et, plus généralement, de macromolécules. Elle nécessite la présence d'atomes avec un numéro atomique assez élevé dans la structure pour provoquer une diffusion anomale observable (à partir du soufre). Généralement, trois longueurs d'onde sont utilisées : avant l'arête d'absorption, sur l'arête d'absorption et après. Il est aussi possible d'utiliser la diffraction anomale avec une seule longueur d'onde (SAD, Single-wavelength anomalous dispersion). Dans ce cas, la longueur d'onde est sélectionnée pour optimiser le contraste entre différents atomes de la structure. Cette technique a l'avantage de minimiser la destruction du cristal par les rayons X.

Le principe est similaire à celui de la méthode du remplacement isomorphe : au lieu de changer les atomes de la structure, c'est la longueur d'onde utilisée pour l'expérience qui varie autour de l'arête d'absorption de l'atome produisant la diffusion anomale. Il existe deux méthodes de détermination de structure par la diffraction anomale : la première utilise la partie imaginaire de la correction anomale, la seconde utilise les variations de la partie réelle en fonction de la longueur d'onde.

Méthode du recuit simulé

Il s'agit d'une méthode de détermination de structure développée en 1997[20] qui opère directement dans l'espace direct. Elle est plus connue en anglais sous le nom de simulated annealing method. Les atomes sont placés au hasard dans la maille et leurs positions sont changées de manière aléatoire à chaque cycle, en comparant les intensités calculées aux intensités observées. Il n'est pas nécessaire de connaître la composition chimique exacte du cristal : deux atomes peuvent être superposés sur la même position, simulant un atome plus lourd. D'autre part, la méthode n'a pas besoin du groupe d'espace du cristal pour fonctionner.

L'algorithme du recuit simulé fonctionne par itérations de cycles. La configuration atomique de départ est choisie aléatoirement. Pour chaque cycle $i$ est calculée la valeur $C_{i}$ d'une « fonction de coût » $C$ , qui doit être minimisée au cycle suivant :

C_{i}=\alpha E+(\alpha -1)R

où $E$ est une fonction obtenue à partir de potentiels interatomiques, α étant choisi entre 0 et 1. $R$ est un facteur d'accord cristallographique défini par la somme des différences entre intensités observées et intensités calculées à partir de la configuration atomique. Si α est égal à 0, seul le facteur d'accord $R$ est pris en compte, ce qui autorise plusieurs atomes à se retrouver sur la même position.

À chaque cycle, toutes les positions atomiques $x$ , $y$ , $z$ sont modifiées. La fonction de coût permet de garder ou de rejeter les changements :

si $C_{i+1}$ > $C_{i}$ , les valeurs du cycle $i$ sont gardées et les changements sont rejetés ;
si $C_{i+1}$ < $C_{i}$ , les nouvelles valeurs sont gardées avec une probabilité $P$ , définie par :

P=\mathrm {e} ^{-(C_{i+1}-C_{i})/K}

où $K$ décroît à chaque cycle. Par analogie avec la statistique de Maxwell-Boltzmann, le paramètre $K$ peut être vu comme une « température » du système, d'où le nom de « recuit simulé ». L'utilisation de la probabilité $P$ permet d'éviter à l'algorithme de rester coincé dans un minimum local de la fonction de coût. Des critères de convergence permettent l'arrêt automatique de l'algorithme, par exemple lorsqu'une certaine valeur de la fonction de coût est atteinte.

Si la composition chimique est connue, il est possible d'imposer des contraintes souples sur les longueurs des liaisons afin d'aider l'algorithme à converger.

Cette méthode est utilisée pour la détermination de structure à partir de données sur poudres[21] et est implémentée dans le programme FullProf[22], par exemple. Au contraire des autres méthodes présentées, celle du recuit simulé peut aussi être utilisée pour des données de diffraction de neutrons, puisqu'elle n'utilise aucune hypothèse sur la densité électronique dans le cristal.

Méthode d'entropie maximum

La méthode d'entropie maximum pour la détermination d'une structure cristalline consiste à reconstruire la densité électronique $\rho$ pour un ensemble de points définissant une grille fine dans la maille, à partir des facteurs de structure observés. Le nombre de points $N$ de la grille étant généralement beaucoup plus grand que le nombre de réflexions observées, il existe une infinité de solutions. La solution choisie est celle qui maximise l'entropie de Shannon $S$ [23] :

S=-\sum _{i=1}^{N}\rho _{i}\cdot ln\left({\frac {\rho _{i}}{\tau _{i}}}\right)

où $\tau$ peut contenir des informations supplémentaires sur la densité électronique, mais est souvent choisi comme une fonction constante. Certaines contraintes sont appliquées lors de la recherche de solution :

l'intégration de la densité électronique dans la maille doit donner le nombre total d'électrons, connu par la formule chimique du composé et sa densité ;
la densité électronique calculée doit reproduire au mieux les facteurs de structure observés.

La connaissance du groupe d'espace du cristal permet d'imposer des contraintes supplémentaires de symétrie à la densité électronique.

Cette méthode peut être utilisée pour les structures modulées[24]. Elle a aussi été appliquée pour des données de diffraction d'électrons[25].

Algoritme de charge flipping

Cette méthode fonctionne sans connaissances a priori sur le contenu de la maille ou sur la symétrie du cristal. Elle utilise uniquement l'hypothèse sur la positivité de la densité électronique. Il s'agit d'une méthode itérative, développée en 2004 et décrite par les séquences suivantes[26].

À chaque facteur de structure $F({\vec {H}})$ est associée une phase aléatoire $\varphi ({\vec {H}})$ . Les phases des facteurs de structure des réflexions non mesurées sont nulles, ainsi que celle de $F({\vec {0}})$ qui est égal au nombre total d'électrons dans la maille et est nécessairement un nombre réel.
À partir de ces phases aléatoires, une densité électronique est calculée par la transformation de Fourier inverse des facteurs de structure.
La densité électronique ainsi calculée peut être négative par endroits, puisque les phases sont aléatoires et ne correspondent pas à la structure du cristal. Elle est alors modifiée : pour les valeurs négatives, le signe est changé, on ne garde que la valeur absolue de la densité (d'où le nom de « charge flipping »).
La transformée de Fourier de cette densité électronique modifiée est calculée : $G({\vec {H}})$ .
Les phases des $G({\vec {H}})$ sont assignées aux facteurs de structure observés $F({\vec {H}})$ ; comme au début, $\varphi ({\vec {0}})=0$ et les phases des réflexions non observées sont remises à 0.
Retour à la deuxième étape jusqu'à ce que la convergence soit atteinte.

La méthode de charge flipping a été appliquée avec succès pour la détermination de structures cristallines inconnues et fonctionne aussi pour les structures modulées, elle est d'ailleurs implémentée dans le programme Jana2006[27]. Il n'existe cependant toujours pas de preuve mathématique de la convergence de l'algorithme.

Fonction de distribution de paires

Cette méthode est adaptée pour des échantillons sous forme de poudre dont les cristallites sont des nanoparticules, ainsi que pour les matériaux amorphes. Elle est aussi appelée « analyse PDF » d'après le terme anglais pair distribution function.

Mesure expérimentale de phases

Il est possible de mesurer la phase d'une réflexion par l'utilisation de faisceaux multiples et de la théorie dynamique de la diffraction[28]. Cette méthode n'est pas une méthode standard en cristallographie et est coûteuse en temps.

Affinement de structure

L'affinement de structure n'est pas à proprement parler une méthode de détermination de structure. À partir du modèle déterminé par une des méthodes citées ci-dessus, les paramètres structuraux (positions des atomes, agitations thermiques…) sont affinés par une méthode de moindres carrés afin de réaliser le meilleur accord possible entre intensités mesurées et intensités calculées.

Lors de l'affinement d'un modèle, il est possible qu'un paramètre atteigne une valeur physiquement absurde : cela indique qu'une espèce chimique dans la structure n'a pas été identifiée correctement. Par exemple, si le paramètre d'agitation thermique isotrope d'un atome devient proche de zéro pour une mesure à température ambiante, cela peut vouloir dire qu'il s'agit d'une autre espèce chimique avec un plus grand numéro atomique : le programme d'affinement compense l'intensité trop faible calculée à partir du modèle en réduisant l'agitation thermique de l'atome. Si au contraire le paramètre d'agitation thermique est beaucoup plus grand que la valeur des autres atomes, cela signifie sans doute qu'un atome de plus faible numéro atomique est présent sur cette position. Enfin, le calcul des distances interatomiques peut aussi permettre d'identifier clairement une espèce chimique dans la structure.

Lorsqu'un atome n'a pas pu être trouvé dans la maille (typiquement, les atomes d'hydrogène, qui ne possèdent qu'un électron et ont une faible interaction avec les rayons X), il est possible de le trouver par examination de la densité électronique différence $\Delta \rho$ , après affinement du reste de la structure. Si F_obs et F_calc désignent les facteurs de structure observés et calculés, respectivement, en assignant les phases obtenues par le modèle aux F_calc, la densité électronique différence s'écrit :

\Delta \rho ({\vec {r}})={\frac {1}{V}}\sum _{\vec {H}}\left[F_{obs}({\vec {H}})-F_{calc}({\vec {H}})\right]\mathrm {e} ^{2i\pi {\vec {H}}\cdot {\vec {r}}}

Notes et références

(en) W.L. Bragg, « The Structure of Some Crystals as Indicated by their Diffraction of X-rays », Proc. R. Soc. Lond. A, vol. 89, n^o 610,‎ 1913, p. 248-277 (DOI 10.1098/rspa.1913.0083)
(en) W.L. Bragg, R.W. James et C.H. Bosanquet, « The Intensity of Reflexion of X-rays by Rock-Salt », Phil. Mag., vol. 41, n^o 243,‎ 1921, p. 309-337 (DOI 10.1080/14786442108636225)
(en) W.L. Bragg, R.W. James et C.H. Bosanquet, « The Intensity of Reflexion of X-rays by Rock-Salt. Part II », Phil. Mag., vol. 42, n^o 247,‎ 1921, p. 1-17 (DOI 10.1080/14786442108633730)
(en) « for their outstanding achievements in the development of direct methods for the determination of crystal structures » in Personnel de rédaction, « The Nobel Prize in Chemistry 1985 », Fondation Nobel, 2010. Consulté le 26 août 2010
(en) D. Harker et J.S. Kasper, « Phases of Fourier coefficients directly from crystal diffraction data », Acta Cryst., vol. 1, n^o 2,‎ 1948, p. 70-75 (DOI 10.1107/S0365110X4800020X)
(en) Herbert Aaron Hauptman et Jerome Karle, Solution of the Phase Problem. I. The Centrosymmetric Crystal, Dayton, Ohio, Polycrystal Book Service, coll. « American Crystallographic Association Monograph » (n^o 3), 1953
(en) Herbert Aaron Hauptman et Jerome Karle, « Structure invariants and seminvariants for noncentrosymmetric space groups », Acta Cryst., vol. 9, n^o 1,‎ 1956, p. 45-55 (DOI 10.1107/S0365110X56000097)
(en) D. Sayre, « The squaring method: a new method for phase determination », Acta Cryst., vol. 5, n^o 1,‎ 1952, p. 60-65 (DOI 10.1107/S0365110X52000137)
(en) A.L. Patterson, « A Fourier Series Method for the Determination of the Components of Interatomic Distances in Crystals », Physical Review, vol. 46, n^o 5,‎ 1934, p. 372-376 (DOI 10.1103/PhysRev.46.372)
(en) David Harker, « The application of the three-dimensional Patterson method and the crystal structures of proustite, Ag₃AsS₃, and pyrargyrite, Ag₃SbS₃ », J. Chem. Phys., vol. 4, n^o 6,‎ 1936, p. 381-390 (DOI 10.1063/1.1749863)
(en) J.M. Cork, « The crystal structure of some of the alums », Philos. Mag., vol. 4, n^o 23,‎ 1927, p. 688-698 (résumé)
(en) International Tables for Crystallography, vol. B : Reciprocal space, U. Shmueli, Kluwer Academic Publishers, 2008, 3^e éd. (ISBN 978-1-4020-8205-4), chap. 2.4 (« Isomorphous replacement and anomalous scattering »), p. 265
(en) C. Bokhoven, J.C. Schoone et J.M. Bijvoet, « The Fourier synthesis of the crystal structure of strychnine sulphate pentahydrate », Acta Cryst., vol. 4, n^o 3,‎ 1951, p. 275-280 (DOI 10.1107/S0365110X51000891)
(en) Alexander McPherson, Preparation and analysis of protein crystals, John Wiley & Sons, 1982, 371 p. (ISBN 978-0-471-08524-9)
(en) Randy J. Read, « Molecular Replacement », sur Structural Medicine (consulté le 15 octobre 2011)
(en) R.J. Fletterick et T.A. Steitz, « The combination of independent phase information obtained from separate protein structure determinations of yeast hexokinase », Acta Cryst., vol. 32, n^o 1,‎ 1976, p. 125-132 (DOI 10.1107/S0567739476000235)
(en) Johannes Martin Bijvoet, « Phase determination in direct Fourier synthesis of crystal structures », Proc. K. Ned. Akad. Wet. B, vol. 52,‎ 1949, p. 313-314 (lire en ligne)
(en) Johannes Martin Bijvoet, A.F. Peerdeman et A.J. van Bommel, « Determination of the Absolute Configuration of Optically Active Compounds by Means of X-Rays », Nature, vol. 168,‎ 1951, p. 271-272 (DOI 10.1038/168271a0)
(en) J.M. Guss, E.A. Merritt, R.P. Phizackerley, B. Hedman, M. Murata, K.O. Hodgson et H.C. Freeman, « Phase determination by multiple-wavelength x-ray diffraction: crystal structure of a basic "blue" copper protein from cucumbers », Science, vol. 241, n^o 4867,‎ 12 août 1988, p. 806-811 (DOI 10.1126/science.3406739)
(en) Yu. G. Andreev, P. Lightfoot et P.G. Bruce, « A General Monte Carlo Approach to Structure Solution from Powder Diffraction Data: Application to Poly(ethylene oxide)₃:LiN(SO₃CF₃)₂ », J. Appl. Cryst., vol. 30, n^o 3,‎ 1997, p. 294-305 (DOI 10.1107/S0021889896013556)
(en) Michael W. Deem et John M. Newsam, « Framework crystal structure solution by simulated annealing: test application to known zeolite structures », J. Am. Chem. Soc., vol. 114, n^o 18,‎ 1992, p. 7189-7198 (DOI 10.1021/ja00044a035)
(en) « FullProf Homepage », sur ILL, Institut Laue-Langevin (consulté le 6 octobre 2011)
(en) Christopher J. Gilmore, « Maximum Entropy and Bayesian Statistics in Crystallography: a Review of Practical Applications », Acta Cryst. A, vol. 52, n^o 4,‎ 1996, p. 561-589 (DOI 10.1107/S0108767396001560)
(en) Lukáš Palatinus et Sander van Smaalen, « Incommensurate modulations made visible by the Maximum Entropy Method in superspace », Zeitschrift für Kristallographie, vol. 219, n^o 11,‎ 2004, p. 719-729 (DOI 10.1524/zkri.219.11.719.52435)
(en) I.G. Voigt-Martin, D.H. Yan, A. Yakimansky, D. Schollmeyer, C.J. Gilmore et G. Bricogne, « Structure determination by electron crystallography using both maximum-entropy and simulation approaches », Acta Cryst. A, vol. 51, n^o 6,‎ 1995, p. 849-868 (DOI 10.1107/S0108767395004557)
(en) Gábor Oszlányi et András Sütő, « The charge flipping algorithm », Acta Cryst. A, vol. 64, n^o 1,‎ 2008, p. 123-134 (DOI 10.1107/S0108767307046028, lire en ligne)
(en) « Jana » (consulté le 6 octobre 2011)
(en) Qun Shen, « Direct measurements of Bragg-reflection phases in x-ray crystallography », Physical Review B, vol. 59, n^o 17,‎ 1999, p. 11109-11112 (DOI 10.1103/PhysRevB.59.11109)

Bibliographie

(en) Carmelo Giacovazzo, Hugo Luis Monaco, Gilberto Artioli, Davide Viterbo, Marco Milanesio, Giovanni Ferraris, Gastone Gilli, Paola Gilli, Giuseppe Zanotti et Michele Catti, Fundamentals of Crystallography, Oxford University Press, 2011, 3^e éd., 864 p. (ISBN 978-0-19-957366-0)
(en) International Tables for Crystallography, vol. B : Reciprocal space, U. Shmueli, Kluwer Academic Publishers, 2008, 3^e éd. (ISBN 978-1-4020-8205-4), chap. 2.2-2.5, p. 210-345
(de) Werner Massa, Kristallstrukturbestimmung, Wiesbaden, Vieweg+Teubner, 2009 (1^re éd. 1994) (ISBN 978-3-8348-0649-9)
(en) W.I.F. David, K. Shankland, L.B. McCusker et C. Bärlocher, Structure Determination from Powder Diffraction Data, Oxford University Press, 2002, 337 p. (ISBN 978-0-19-850091-9, lire en ligne)

Voir aussi

Liens externes

(en) Nicolas Schoeni et Gervais Chapuis, « Charge Flipping », sur École Polytechnique Fédérale de Lausanne (consulté le 6 octobre 2011). Application Java sur la méthode de charge flipping.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.