Équation d'état cubique

En thermodynamique, une équation d'état cubique est une équation d'état d'un fluide pouvant s'écrire sous la forme d'un polynôme de degré trois en fonction du volume.

Elles ont une forme générale de polynôme du troisième degré en $Z$ , le facteur de compressibilité :

Équation d'état cubique :

Z^{3}+c_{2}Z^{2}+c_{1}Z+c_{0}=0

avec $c_{2}{,}\,c_{1}{,}\,c_{0}$ des paramètres qui ne dépendent que de la pression, de la température et de la composition du mélange, le volume n'apparaissant que dans le facteur de compressibilité. Sous cette forme, ces équations sont facilement utilisables en appliquant la méthode de Cardan pour trouver le volume d'un fluide.

Historique

Figure 1 - Courbes à température constante (isothermes) de l'équation d'état de van der Waals dans un diagramme de Clapeyron.
En rouge : l'isotherme critique ; le point critique est noté C. Au-dessus (courbes vertes) le fluide est supercritique. Au-dessous (courbes bleues) le fluide peut être liquide (point L) ou gazeux (point G).

La première équation d'état cubique est celle de Johannes Diderik van der Waals et date de 1873 ; elle valut le prix Nobel de physique en 1910 à son concepteur. Van der Waals introduisit les notions d'interaction à distance et de taille des molécules dans son équation, ce qui la différencie fondamentalement du modèle des gaz parfaits dans lequel les molécules sont des sphères dures sans dimension qui n'interagissent entre elles que par collision. La grande nouveauté de cette équation fut de prédire un point critique et la transition de phase gaz-liquide (voir Figure 1). Cette équation et toutes celles qui lui ont succédé présentent néanmoins un certain nombre de défauts inhérents à la forme, dont celui de mal représenter le point critique et de surévaluer systématiquement le volume des liquides.

Cependant, la simplicité de ce modèle, sa facilité d'utilisation et la possibilité de calculer les équilibres liquide-vapeur conduisirent de nombreux chercheurs à en proposer des développements. La liste d'équations présentée dans cet article n'est pas exhaustive[1] et ne pourrait pas l'être étant donné la profusion de publications concernant ces équations[2]. La sélection effectuée se base sur des critères tant liés à l'histoire qu'à l'intérêt pratique des équations. L'équation de van der Waals par exemple est présentée parce qu'elle est la première des équations d'état cubiques, mais son imprécision l'a fait abandonner dans la pratique, hormis dans le domaine de l'enseignement où sa simplicité la rend facilement manipulable. Les équations d'état de Soave-Redlich-Kwong (1972) et de Peng-Robinson (1976) sont encore d'usage courant dans l'industrie et font toujours l'objet de nombreuses études[3].

Équations diverses

Équation de van der Waals (1873)

Cette équation d'état, la première équation d'état cubique, a été proposée en 1873 par Johannes Diderik van der Waals[4]. Elle valut à celui-ci le prix Nobel de physique de 1910 « pour ses travaux sur l'équation d'état des gaz et des liquides »[5]. Elle est la première équation d'état qui, en tenant compte des interactions entre molécules via le paramètre $a$ et de la taille de celles-ci via le paramètre $b$ , représente la transition de phase liquide-gaz et le point critique. Elle se présente sous la forme :

Équation de van der Waals :

P={RT \over {\bar {V}}-b}-{a \over {\bar {V}}^{2}}

Elle a pour forme polynomiale :

Équation de van der Waals :

Z^{3}-\left(B+1\right)Z^{2}+AZ-AB=0

Pour un corps pur, les paramètres $a$ (constant) et $b$ sont calculés à partir des pression et température critiques (mesurables expérimentalement) selon :

Pour un corps pur :

a={27 \over 64}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}

b={1 \over 8}{R{T_{\mathrm {c} }} \over P_{\mathrm {c} }}

Le paramètre $a$ est généralement écrit sous la forme $a=\Omega _{a}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)$ . Pour l'équation de van der Waals, $\Omega _{a}={27 \over 64}$ et $\alpha \!\left(T\right)=1$ .

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ et $P_{\mathrm {c} }$ .

Équation de Clausius (1880)

L'équation de van der Waals souffre de nombreux défauts, dont ceux de ne pas représenter correctement le volume critique et la capacité thermique isochore. Dès 1880 Rudolf Clausius, qui auparavant avait complété l'énoncé du deuxième principe de la thermodynamique (1850) et inventé le concept d'entropie (1865), proposa une amélioration de l'équation d'état de van der Waals[6] - [7] - [8]. Cette équation tente de corriger le défaut de l'équation de van der Waals au point critique en introduisant un terme correctif $c$ et celui concernant la capacité thermique isochore en faisant dépendre le paramètre $a$ de la température. L'équation de Clausius prend la forme :

Équation de Clausius :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over \left({\bar {V}}+c\right)^{2}}

Elle a pour forme polynomiale :

Équation de Clausius :

Z^{3}+\left(2C-B-1\right)Z^{2}+\left(C^{2}-2BC-2C+A\right)Z-\left(BC^{2}+C^{2}+AB\right)=0

Pour un corps pur, les paramètres $a$ , $b$ et $c$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a={27 \over 64}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)

b={\bar {V}}_{\mathrm {c} }-{1 \over 4}{R{T_{\mathrm {c} }} \over P_{\mathrm {c} }}

c={3 \over 8}{R{T_{\mathrm {c} }} \over P_{\mathrm {c} }}-{\bar {V}}_{\mathrm {c} }

avec :

\alpha \!\left(T\right)={1 \over T_{\mathrm {r} }}

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ , $P_{\mathrm {c} }$ et ${\bar {V}}_{\mathrm {c} }$ (ou $Z_{\mathrm {c} }$ ).

Équation de Berthelot (1899)

Le paramètre $c$ de l'équation de Clausius étant petit devant $b$ , Daniel Berthelot propose en 1899 de considérer que $c=0$ [9] - [10] - [11]. Son équation prend la forme :

Équation de Berthelot :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over {\bar {V}}^{2}}

Elle a pour forme polynomiale :

Équation de Berthelot :

Z^{3}-\left(B+1\right)Z^{2}+AZ-AB=0

Pour un corps pur, les paramètres $a$ et $b$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a=8P_{\mathrm {c} }{{\bar {V}}_{\mathrm {c} }}^{2}\cdot \alpha \!\left(T\right)

b={{\bar {V}}_{\mathrm {c} } \over 3}

avec :

\alpha \!\left(T\right)={1 \over T_{\mathrm {r} }}

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ , $P_{\mathrm {c} }$ et ${\bar {V}}_{\mathrm {c} }$ (ou $Z_{\mathrm {c} }$ ).

Équation de Redlich-Kwong (1949)

En 1949 Otto Redlich et Joseph Neng Shun Kwong proposent une nouvelle modification du terme attractif de l'équation de van der Waals[12] - [13] :

Équation de Redlich-Kwong :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over {\bar {V}}\left({\bar {V}}+b\right)}

Elle a pour forme polynomiale :

Équation de Redlich-Kwong :

Z^{3}-Z^{2}+\left(-B^{2}-B+A\right)Z-AB=0

Pour un corps pur, les paramètres $a$ et $b$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a={1 \over 9\left({\sqrt[{3}]{2}}-1\right)}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)=0,42748{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)

b={{\sqrt[{3}]{2}}-1 \over 3}{RT_{\mathrm {c} } \over P_{\mathrm {c} }}=0,08664{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

avec :

\alpha \!\left(T\right)={1 \over {\sqrt {T_{\mathrm {r} }}}}

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ et $P_{\mathrm {c} }$ .

Équation de Soave-Redlich-Kwong (1972)

En 1972 Giorgio Soave propose une modification de la fonction $\alpha$ de l'équation de Redlich-Kwong en y introduisant le facteur acentrique $\omega$ [14]. Cette nouvelle équation est appelée équation de Soave-Redlich-Kwong ou de Redlich-Kwong-Soave. Elle est de la forme :

Équation de Soave-Redlich-Kwong :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over {\bar {V}}\left({\bar {V}}+b\right)}

Elle a pour forme polynomiale :

Équation de Soave-Redlich-Kwong :

Z^{3}-Z^{2}+\left(-B^{2}-B+A\right)Z-AB=0

Pour un corps pur, les paramètres $a$ et $b$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a={1 \over 9\left({\sqrt[{3}]{2}}-1\right)}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)=0,42748{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)

b={{\sqrt[{3}]{2}}-1 \over 3}{RT_{\mathrm {c} } \over P_{\mathrm {c} }}=0,08664{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

avec :

\alpha \!\left(T\right)=\left(1+m\cdot \left(1-{T_{\mathrm {r} }}^{0,5}\right)\right)^{2}

m=0,480+1,574\,\omega -0,176\,\omega ^{2}

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ , $P_{\mathrm {c} }$ et $\omega$ .

Équation de Peng-Robinson (1976-1978)

En 1976 Ding-Yu Peng et Donald Robinson proposent une nouvelle modification du terme attractif de l'équation de van der Waals[15]. Cette équation est de la forme :

Équation de Peng-Robinson :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over {\bar {V}}^{2}+2b{\bar {V}}-b^{2}}

Elle a pour forme polynomiale :

Équation de Peng-Robinson :

Z^{3}+\left(B-1\right)Z^{2}+\left(-3B^{2}-2B+A\right)Z+\left(B^{3}+B^{2}-AB\right)=0

Pour un corps pur, les paramètres $a$ et $b$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a=0,45724{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)

b=0,07780{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

avec :

\alpha \!\left(T\right)=\left(1+m\cdot \left(1-{T_{\mathrm {r} }}^{0,5}\right)\right)^{2}

m=0,37464+1,54226\,\omega -0,26992\,\omega ^{2}

Cette équation est appelée Peng-Robinson 76.

En 1978, Peng et Robinson modifient la fonction $m$ selon[16] :

m=0,37464+1,54226\,\omega -0,26992\,\omega ^{2}\qquad

\omega \leq 0,491

m=0,379642+1,487503\,\omega -0,164423\,\omega ^{2}-0,016666\,\omega ^{3}\qquad

sinon

Cette équation est appelée Peng-Robinson 78.

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ , $P_{\mathrm {c} }$ et $\omega$ .

Équation de Patel-Teja (1982)

En 1982 Navin C. Patel et Amin S. Teja proposent une nouvelle modification du terme attractif de l'équation de van der Waals afin de mieux prendre en compte le facteur de compressibilité critique $Z_{\mathrm {c} }$ via un paramètre $c$ [17] - [18]. Cette équation est de la forme :

Équation de Patel-Teja :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over {\bar {V}}\left({\bar {V}}+b\right)+c\left({\bar {V}}-b\right)}

Elle a pour forme polynomiale :

Équation de Patel-Teja :

Z^{3}+\left(C-1\right)Z^{2}+\left(-2BC-B^{2}-B-C+A\right)Z+\left(B^{2}C+BC-AB\right)=0

Pour un corps pur, les paramètres $a$ , $b$ et $c$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a=\Omega _{a}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)

b=\Omega _{b}{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

c=\Omega _{c}{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

avec :

\alpha \!\left(T\right)=\left(1+m\cdot \left(1-{T_{\mathrm {r} }}^{0,5}\right)\right)^{2}

m=0,452413+1,30982\,\omega -0,295937\,\omega ^{2}

Le facteur de compressibilité critique $Z_{\mathrm {c} }$ peut être la valeur expérimentale ou être calculé, pour les fluides apolaires, selon :

Z_{\mathrm {c} }=0,329032-0,076799\,\omega +0,0211947\,\omega ^{2}

Le paramètre $\Omega _{b}$ est la plus petite racine réelle de l'équation :

{\Omega _{b}}^{3}+\left(2-3Z_{\mathrm {c} }\right){\Omega _{b}}^{2}+3{Z_{\mathrm {c} }}^{2}\Omega _{b}-{Z_{\mathrm {c} }}^{3}=0

Les paramètres $\Omega _{a}$ et $\Omega _{c}$ sont ensuite calculés selon :

\Omega _{a}=3{Z_{\mathrm {c} }}^{2}+3\left(1-Z_{\mathrm {c} }\right)\Omega _{b}+{\Omega _{b}}^{2}+1-2Z_{\mathrm {c} }

\Omega _{c}=1-3Z_{\mathrm {c} }

Cette équation est proche de celle de Soave-Redlich-Kwong si $\omega =0$ et de celle de Peng-Robinson si $\omega =0,3$ .

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ , $P_{\mathrm {c} }$ , $\omega$ et ${\bar {V}}_{\mathrm {c} }$ (ou $Z_{\mathrm {c} }$ ).

Équation de Patel-Teja-Valderrama (1990)

En 1990, la complexité de la formulation de l'équation de Patel-Teja et sa limitation aux fluides apolaires conduisent José O. Valderrama à en proposer une forme généralisée, plus simple mathématiquement et applicable également aux fluides polaires[19]. Cette équation est de la forme :

Équation de Patel-Teja-Valderrama :

P={RT \over {\bar {V}}-b}-{a\!\left(T\right) \over {\bar {V}}\left({\bar {V}}+b\right)+c\left({\bar {V}}-b\right)}

Elle a pour forme polynomiale :

Équation de Patel-Teja-Valderrama :

Z^{3}+\left(C-1\right)Z^{2}+\left(-2BC-B^{2}-B-C+A\right)Z+\left(B^{2}C+BC-AB\right)=0

Pour un corps pur, les paramètres $a$ , $b$ et $c$ sont calculés à partir des coordonnées du point critique (mesurables expérimentalement) selon :

Pour un corps pur :

a=\Omega _{a}{R^{2}{T_{\mathrm {c} }}^{2} \over P_{\mathrm {c} }}\cdot \alpha \!\left(T\right)

b=\Omega _{b}{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

c=\Omega _{c}{RT_{\mathrm {c} } \over P_{\mathrm {c} }}

avec :

\alpha \!\left(T\right)=\left(1+m\cdot \left(1-{T_{\mathrm {r} }}^{0,5}\right)\right)^{2}

m=0,46283+3,58230\,\omega Z_{\mathrm {c} }+8,19417\,\left(\omega Z_{\mathrm {c} }\right)^{2}

Les paramètres $\Omega _{a}$ , $\Omega _{b}$ et $\Omega _{c}$ sont calculés selon :

\Omega _{a}=0,66121\,-0,76105\,Z_{\mathrm {c} }

\Omega _{b}=0,02207\,+0,20868\,Z_{\mathrm {c} }

\Omega _{c}=0,57765\,-1,87080\,Z_{\mathrm {c} }

Cette équation nécessite la connaissance de $T_{\mathrm {c} }$ , $P_{\mathrm {c} }$ , $\omega$ et ${\bar {V}}_{\mathrm {c} }$ (ou $Z_{\mathrm {c} }$ ).

Formes généralisées

Toutes les équations d'état cubiques présentées précédemment peuvent être représentées sous les deux formes généralisées suivantes :

Équation d'état cubique généralisée (FG1)

P={RT \over {\bar {V}}-b}-{a \over {\bar {V}}^{2}+ub{\bar {V}}+wb^{2}}

(FG2)

P={RT \over {\bar {V}}-b}-{a \over \left({\bar {V}}-br_{1}\right)\left({\bar {V}}-br_{2}\right)}

Les paramètres $u$ , $w$ , $r_{1}$ et $r_{2}$ sont des nombres réels adimensionnels. Ils sont liés par les relations :

u=-\left(r_{1}+r_{2}\right)

w=r_{1}\cdot r_{2}

et réciproquement :

r_{1}=-{u \over 2}+{\sqrt {{u^{2} \over 4}-w}}

r_{2}=-{u \over 2}-{\sqrt {{u^{2} \over 4}-w}}

Selon l'équation d'état et les règles de mélange appliquées, les paramètres $u$ , $w$ , $r_{1}$ et $r_{2}$ peuvent dépendre de la température et de la composition. Le tableau suivant donne l'expression de ces paramètres pour les différentes équations d'état vues précédemment.

Paramètres des équations d'état cubiques
Équation d'état cubique	$u$	$w$	$r_{1}$	$r_{2}$
van der Waals Berthelot	$0$	$0$	$0$	$0$
Clausius	$2{c \over b}$	$\left({c \over b}\right)^{2}$	$-{c \over b}$	$-{c \over b}$
Redlich-Kwong Soave-Redlich-Kwong	$1$	$0$	$0$	$-1$
Peng-Robinson	$2$	$-1$	$-1+{\sqrt {2}}$	$-1-{\sqrt {2}}$
Patel-Teja Patel-Teja-Valderrama	$1+{c \over b}$	$-{c \over b}$	$-{1 \over 2}\left(1+{c \over b}+{\sqrt {1+6{c \over b}+\left({c \over b}\right)^{2}}}\right)$	$-{1 \over 2}\left(1+{c \over b}-{\sqrt {1+6{c \over b}+\left({c \over b}\right)^{2}}}\right)$

On pose également la forme généralisée :

Équation d'état cubique généralisée (FG3)

P={RT \over {\bar {V}}-b}-{a \over \left({\bar {V}}+b_{1}\right)\left({\bar {V}}+b_{2}\right)}

avec $b_{1}=-br_{1}$ et $b_{2}=-br_{2}$ .

Par définition, toutes les équations d'état cubiques peuvent se mettre sous la forme générale de polynôme du troisième degré en $Z$ , le facteur de compressibilité :

Équation d'état cubique généralisée : (FP)

Z^{3}+c_{2}Z^{2}+c_{1}Z+c_{0}=0

avec :

$c_{2}{,}\,c_{1}{,}\,c_{0}$ des paramètres qui ne dépendent que de la pression $P$ , de la température $T$ et de la composition (fractions molaires $x_{i}$ ),
$Z={P{\bar {V}} \over RT}$ le facteur de compressibilité, $R$ étant la constante universelle des gaz parfaits.

Le volume molaire ${\bar {V}}$ n'apparait que dans le facteur de compressibilité $Z$ .

Le tableau suivant donne la valeur de ces paramètres pour les différentes équations d'état vues précédemment.

Paramètres des équations d'état cubiques
Équation d'état cubique	$c_{2}$	$c_{1}$	$c_{0}$
van der Waals Berthelot	$-B-1$	$A$	$-AB$
Clausius	$2C-B-1$	$C^{2}-2BC-2C+A$	$-BC^{2}-C^{2}-AB$
Redlich-Kwong Soave-Redlich-Kwong	$-1$	$-B^{2}-B+A$	$-AB$
Peng-Robinson	$B-1$	$-3B^{2}-2B+A$	$B^{3}+B^{2}-AB$
Patel-Teja Patel-Teja-Valderrama	$C-1$	$-2BC-B^{2}-B-C+A$	$B^{2}C+BC-AB$

Règles de mélange

Les règles de mélange permettent l'application des équations d'état aux mélanges, c'est-à-dire de calculer les paramètres $a$ , $b$ et $c$ , notés respectivement $a_{m}$ , $b_{m}$ et $c_{m}$ , pour un mélange. Ces paramètres font intervenir la composition du mélange via les fractions molaires de ses constituants $x_{i}$ et les paramètres $a_{i}$ , $b_{i}$ et $c_{i}$ du corps $i$ pur pour chacun des $N$ corps du mélange.

Règles classiques - van der Waals (1890)

Ces règles sont dues à van der Waals (1890[20]) pour l'application de son équation d'état aux mélanges. Ces règles sont appelées règles de mélange classiques :

Règles de mélange classiques :

a_{m}=\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}{\sqrt {a_{i}a_{j}}}\left(1-k_{i,j}\right)

b_{m}=\sum _{i=1}^{N}x_{i}b_{i}

c_{m}=\sum _{i=1}^{N}x_{i}c_{i}

avec $k_{i,j}$ un paramètre d'interaction binaire entre le corps $i$ et le corps $j$ , déterminé expérimentalement, avec $k_{i,j}=k_{j,i}$ et $k_{i,i}=0$ .

Variantes

Il existe des variantes de ces règles, l'une des plus simples consistant à calculer le covolume selon :

b_{m}={1 \over 2}\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left(b_{i}+b_{j}\right)\left(1-l_{i,j}\right)

avec $l_{i,j}$ un paramètre d'interaction binaire entre le corps $i$ et le corps $j$ , déterminé expérimentalement, avec $l_{i,j}=l_{j,i}$ et $l_{i,i}=0$ . Si tous les $l_{i,j}$ sont nuls, cette règle revient à la règle classique.

Une autre variante consiste à calculer le covolume selon une combinaison des diamètres des particules :

{b_{m}}^{\frac {1}{3}}={1 \over 2}\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left({b_{i}}^{\frac {1}{3}}+{b_{j}}^{\frac {1}{3}}\right)\left(1-l_{i,j}\right)

ou de la surface de leur section :

{b_{m}}^{\frac {2}{3}}={1 \over 2}\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left({b_{i}}^{\frac {2}{3}}+{b_{j}}^{\frac {2}{3}}\right)\left(1-l_{i,j}\right)

Règles de Huron-Vidal (1979)

En 1979 Huron et Vidal[21] proposent des règles dans lesquelles le covolume du mélange est calculé selon la règle de van der Waals :

b_{m}=\sum _{i=1}^{N}x_{i}b_{i}

Mais le terme de cohésion, pour une équation d'état sans paramètre $c$ (van der Waals, Berthelot, Redlich-Kwong, Preng-Robinson...), est calculé selon :

{a_{m} \over b_{m}}=\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}+{{\bar {G}}_{\gamma }^{\text{E}} \over {\mathcal {C}}}

avec :

${\mathcal {C}}$ une constante propre à chaque équation d'état : ${\mathcal {C}}={1 \over r_{1}-r_{2}}\ln \!\left({1-r_{1} \over 1-r_{2}}\right)$ avec $r_{1}$ et $r_{2}$ les paramètres de la forme généralisée (FG2) de l'équation d'état cubique ; si $r_{1}=r_{2}$ (y compris si $r_{1}=r_{2}=0$ ), alors ${\mathcal {C}}=-{1 \over 1-r_{1}}$ ;
${\bar {G}}_{\gamma }^{\text{E}}$ un modèle d'enthalpie libre molaire d'excès extérieur à l'équation d'état (comme les modèles de Margules, Van Laar (en), Wilson, NRTL (en), UNIQUAC, UNIFAC ou COSMOSPACE).

Pour une équation d'état avec un paramètre $c$ (Clausius, Patel-Teja...), il faut ajouter la règle de mélange :

c_{m}=\sum _{i=1}^{N}x_{i}c_{i}

et modifier la règle de mélange du paramètre de cohésion :

{a_{m} \over b_{m}}=\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{{\mathcal {C}}_{i} \over {\mathcal {C}}_{m}}+{{\bar {G}}_{\gamma }^{\text{E}} \over {\mathcal {C}}_{m}}

avec :

${\mathcal {C}}_{m}$ la constante ${\mathcal {C}}$ calculée pour le mélange ;
${\mathcal {C}}_{i}$ la constante ${\mathcal {C}}$ calculée pour le corps $i$ pur.

Le principal défaut de ces règles est qu'elles prennent pour référence un état à pression infinie, or les modèles d'enthalpie libre molaire d'excès ${\bar {G}}_{\gamma }^{\text{E}}$ sont développés pour des pressions de l'ordre de la pression atmosphérique. Afin de corriger ce défaut, ces règles ont fait l'objet de deux modifications importantes par Michelsen en 1990[22] et par Dahl et Michelsen également en 1990[23].

Démonstration

L'enthalpie libre molaire idéale d'un mélange liquide s'écrit :

{\bar {G}}_{m}^{\text{l,id}}=\sum _{i=1}^{N}x_{i}\left[{\bar {G}}_{i}^{\text{l,*}}+RT\,\ln x_{i}\right]

avec :

${\bar {G}}_{m}^{\text{l,id}}$ l'enthalpie libre molaire du mélange liquide idéal aux mêmes pression, température et composition que le mélange réel ;
${\bar {G}}_{i}^{\text{l,*}}$ l'enthalpie libre molaire du corps $i$ pur à l'état liquide aux mêmes pression et température que le mélange réel ;
$x_{i}$ la fraction molaire du corps $i$ .

L'enthalpie libre molaire d'excès d'une phase liquide s'écrit :

{\bar {G}}_{m}^{\text{E}}={\bar {G}}_{m}^{\text{l}}-{\bar {G}}_{m}^{\text{l,id}}={\bar {G}}_{m}^{\text{l}}-\sum _{i=1}^{N}x_{i}\left[{\bar {G}}_{i}^{\text{l,*}}+RT\,\ln x_{i}\right]

avec :

${\bar {G}}_{m}^{\text{E}}$ l'enthalpie libre molaire d'excès ;
${\bar {G}}_{m}^{\text{l}}$ l'enthalpie libre molaire du mélange liquide réel.

L'enthalpie libre molaire du mélange de gaz parfaits correspondant au mélange liquide réel s'écrit :

{\bar {G}}_{m}^{\bullet }=\sum _{i=1}^{N}x_{i}\left[{\bar {G}}_{i}^{\bullet ,*}+RT\,\ln x_{i}\right]

avec :

${\bar {G}}_{m}^{\bullet }$ l'enthalpie libre molaire du mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel ;
${\bar {G}}_{i}^{\bullet ,*}$ l'enthalpie libre molaire du corps $i$ à l'état de gaz parfait pur aux mêmes pression et température que le mélange réel.

On introduit l'enthalpie libre molaire du mélange de gaz parfaits dans l'enthalpie libre molaire d'excès :

{\bar {G}}_{m}^{\text{E}}={\bar {G}}_{m}^{\text{l}}-{\bar {G}}_{m}^{\bullet }-\sum _{i=1}^{N}x_{i}\left[{\bar {G}}_{i}^{\text{l,*}}+RT\,\ln x_{i}\right]+{\bar {G}}_{m}^{\bullet }=\left[{\bar {G}}_{m}^{\text{l}}-{\bar {G}}_{m}^{\bullet }\right]-\sum _{i=1}^{N}x_{i}\left[{\bar {G}}_{i}^{\text{l,*}}-{\bar {G}}_{i}^{\bullet ,*}\right]

On reconnait les enthalpies libres molaires résiduelles du mélange et de chacun des corps purs :

{\bar {G}}_{m}^{\text{l,RES}}={\bar {G}}_{m}^{\text{l}}-{\bar {G}}_{m}^{\bullet }

{\bar {G}}_{i}^{\text{l,*,RES}}={\bar {G}}_{i}^{\text{l,*}}-{\bar {G}}_{i}^{\bullet ,*}

avec :

${\bar {G}}_{m}^{\text{l,RES}}$ l'enthalpie libre molaire résiduelle du mélange ;
${\bar {G}}_{i}^{\text{l,*,RES}}$ l'enthalpie libre molaire résiduelle du corps $i$ pur.

On a donc :

{\bar {G}}_{m}^{\text{E}}={\bar {G}}_{m}^{\text{l,RES}}-\sum _{i=1}^{N}x_{i}{\bar {G}}_{i}^{\text{l,*,RES}}

L'enthalpie libre molaire d'un mélange liquide s'écrit, avec la forme généralisée (FG2) des équations d'état cubiques :

{\bar {G}}_{m}^{\text{l,RES}}\!\left(P,T,z\right)={\bar {G}}_{m}^{\text{l}}\!\left(P,T,z\right)-{\bar {G}}_{m}^{\bullet }\!\left(P,T,z\right)={a_{m} \over b_{m}}{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},n\right)+P{\bar {V}}_{m}^{\text{l}}-RT-RT\,\ln \!\left({P\left({\bar {V}}_{m}^{\text{l}}-b_{m}\right) \over RT}\right)

L'enthalpie libre molaire résiduelle d'un liquide pur s'écrit, avec la forme généralisée (FG2) des équations d'état cubiques :

{\bar {G}}_{i}^{\text{l,*,RES}}\!\left(P,T\right)={\bar {G}}_{i}^{\text{l,*}}\!\left(P,T\right)-{\bar {G}}_{i}^{\bullet ,*}\!\left(P,T\right)={a_{i} \over b_{i}}{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}}\right)+P{\bar {V}}_{i}^{\text{l,*}}-RT-RT\,\ln \!\left({P\left({\bar {V}}_{i}^{\text{l,*}}-b_{i}\right) \over RT}\right)

En remplaçant les enthalpies libres résiduelles par leur expression et en réarrangeant on a :

{\bar {G}}_{m}^{\text{E}}={a_{m} \over b_{m}}{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},n\right)-\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}}\right)+P\left[{\bar {V}}_{m}^{\text{l}}-\sum _{i=1}^{N}x_{i}{\bar {V}}_{i}^{\text{l,*}}\right]+\sum _{i=1}^{N}x_{i}RT\,\ln \!\left({{\bar {V}}_{i}^{\text{l,*}}-b_{i} \over {\bar {V}}_{m}^{\text{l}}-b_{m}}\right)

On pose la règle de mélange identique à celle de van der Waals pour le covolume :

b_{m}=\sum _{i=1}^{N}x_{i}b_{i}

on a :

{\bar {G}}_{m}^{\text{E}}={a_{m} \over b_{m}}{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},n\right)-\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}}\right)+P\left[\left({\bar {V}}_{m}^{\text{l}}-b_{m}\right)-\sum _{i=1}^{N}x_{i}\left({\bar {V}}_{i}^{\text{l,*}}-b_{i}\right)\right]+\sum _{i=1}^{N}x_{i}RT\,\ln \!\left({{\bar {V}}_{i}^{\text{l,*}}-b_{i} \over {\bar {V}}_{m}^{\text{l}}-b_{m}}\right)

Pour le mélange et le corps pur :

\lim _{P\to +\infty }{\bar {V}}_{m}^{\text{l}}=b_{m}

\lim _{P\to +\infty }{\bar {V}}_{i}^{\text{l,*}}=b_{i}

\lim _{P\to +\infty }{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},z\right)={\mathcal {C}}_{m}

\lim _{P\to +\infty }{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}},z\right)={\mathcal {C}}_{i}

D'où, à pression infinie :

{\bar {G}}_{m}^{\text{E}}\!\left(P=+\infty \right)={a_{m} \over b_{m}}{\mathcal {C}}_{m}-\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{\mathcal {C}}_{i}

{a_{m} \over b_{m}}=\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{{\mathcal {C}}_{i} \over {\mathcal {C}}_{m}}+{{\bar {G}}_{m}^{\text{E}}\!\left(P=+\infty \right) \over {\mathcal {C}}_{m}}

Si ${\mathcal {C}}_{m}={\mathcal {C}}_{i}$ , c'est-à-dire si les paramètres $r_{1}$ et $r_{2}$ de la forme généralisée (FG2) des équations d'état cubiques sont les mêmes pour un corps pur et pour un mélange, ce qui exclut les équations possédant un paramètre $c$ (Clausius, Patel-Teja...) :

{a_{m} \over b_{m}}=\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}+{{\bar {G}}_{m}^{\text{E}}\!\left(P=+\infty \right) \over {\mathcal {C}}}

Règles de Wong-Sandler (1992)

En 1992 Wong et Sandler[24] proposent, pour une équation d'état sans paramètre $c$ (van der Waals, Berthelot, Redlich-Kwong, Preng-Robinson...), de modifier la règle de mélange du covolume selon :

b_{m}={\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left(b-{a \over RT}\right)_{i,j} \over 1-\left(\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}RT}+{{\bar {G}}_{\gamma }^{\text{E}} \over {\mathcal {C}}RT}\right)}

avec :

${\mathcal {C}}$ une constante propre à chaque équation d'état : ${\mathcal {C}}={1 \over r_{1}-r_{2}}\ln \!\left({1-r_{1} \over 1-r_{2}}\right)$ avec $r_{1}$ et $r_{2}$ les paramètres de la forme généralisée (FG2) de l'équation d'état cubique ; si $r_{1}=r_{2}$ (y compris si $r_{1}=r_{2}=0$ ), alors ${\mathcal {C}}=-{1 \over 1-r_{1}}$ ;
${\bar {G}}_{\gamma }^{\text{E}}$ un modèle d'enthalpie libre molaire d'excès extérieur à l'équation d'état (comme les modèles de Margules, Van Laar (en), Wilson, NRTL (en), UNIQUAC, UNIFAC ou COSMOSPACE) ;
$\left(b-{a \over RT}\right)_{i,j}={1 \over 2}\left[\left(b_{i}-{a_{i} \over RT}\right)+\left(b_{j}-{a_{j} \over RT}\right)\right]\left(1-k_{i,j}\right)$ ; $k_{i,j}$ étant un paramètre d'interaction binaire entre le corps $i$ et le corps $j$ , déterminé expérimentalement, avec $k_{i,j}=k_{j,i}$ et $k_{i,i}=0$ .

Le terme de cohésion est calculé selon :

b_{m}-{a_{m} \over RT}=\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left(b-{a \over RT}\right)_{i,j}

Pour une équation d'état avec un paramètre $c$ (Clausius, Patel-Teja...), il faut ajouter la règle de mélange :

c_{m}=\sum _{i=1}^{N}x_{i}c_{i}

et modifier la règle de mélange du covolume :

b_{m}={\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left(b-{a \over RT}\right)_{i,j} \over 1-\left(\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}RT}{{\mathcal {C}}_{i} \over {\mathcal {C}}_{m}}+{{\bar {G}}_{\gamma }^{\text{E}} \over {\mathcal {C}}_{m}RT}\right)}

avec :

${\mathcal {C}}_{m}$ la constante ${\mathcal {C}}$ calculée pour le mélange ;
${\mathcal {C}}_{i}$ la constante ${\mathcal {C}}$ calculée pour le corps $i$ pur.

Contrairement aux règles de van der Waals et de Huron-Vidal, les règles de Wong-Sandler impliquent une dépendance du paramètre $b_{m}$ à la température, même si les paramètres $b_{i}$ des corps purs sont des constantes.

Démonstration

L'énergie libre molaire idéale d'un mélange liquide s'écrit :

{\bar {F}}_{m}^{\text{l,id}}=\sum _{i=1}^{N}x_{i}\left[{\bar {F}}_{i}^{\text{l,*}}+RT\,\ln x_{i}\right]

avec :

${\bar {F}}_{m}^{\text{l,id}}$ l'énergie libre molaire du mélange liquide idéal aux mêmes pression, température et composition que le mélange réel ;
${\bar {F}}_{i}^{\text{l,*}}$ l'énergie libre molaire du corps $i$ pur à l'état liquide aux mêmes pression et température que le mélange réel ;
$x_{i}$ la fraction molaire du corps $i$ .

L'énergie libre molaire d'excès d'une phase liquide s'écrit :

{\bar {F}}_{m}^{\text{E}}={\bar {F}}_{m}^{\text{l}}-{\bar {F}}_{m}^{\text{l,id}}={\bar {F}}_{m}^{\text{l}}-\sum _{i=1}^{N}x_{i}\left[{\bar {F}}_{i}^{\text{l,*}}+RT\,\ln x_{i}\right]

avec :

${\bar {F}}_{m}^{\text{E}}$ l'énergie libre molaire d'excès ;
${\bar {F}}_{m}^{\text{l}}$ l'énergie libre molaire du mélange liquide réel.

L'énergie libre molaire du mélange de gaz parfaits correspondant au mélange liquide réel s'écrit :

{\bar {F}}_{m}^{\bullet }=\sum _{i=1}^{N}x_{i}\left[{\bar {F}}_{i}^{\bullet ,*}+RT\,\ln x_{i}\right]

avec :

${\bar {F}}_{m}^{\bullet }$ l'énergie libre molaire du mélange de gaz parfaits aux mêmes pression, température et composition que le mélange réel ;
${\bar {F}}_{i}^{\bullet ,*}$ l'énergie libre molaire du corps $i$ à l'état de gaz parfait pur aux mêmes pression et température que le mélange réel.

On introduit l'énergie libre molaire du mélange de gaz parfaits dans l'énergie libre molaire d'excès :

{\bar {F}}_{m}^{\text{E}}={\bar {F}}_{m}^{\text{l}}-{\bar {F}}_{m}^{\bullet }-\sum _{i=1}^{N}x_{i}\left[{\bar {F}}_{i}^{\text{l,*}}+RT\,\ln x_{i}\right]+{\bar {F}}_{m}^{\bullet }=\left[{\bar {F}}_{m}^{\text{l}}-{\bar {F}}_{m}^{\bullet }\right]-\sum _{i=1}^{N}x_{i}\left[{\bar {F}}_{i}^{\text{l,*}}-{\bar {F}}_{i}^{\bullet ,*}\right]

On reconnait les énergies libres molaires résiduelles du mélange et de chacun des corps purs :

{\bar {F}}_{m}^{\text{l,RES}}={\bar {F}}_{m}^{\text{l}}-{\bar {F}}_{m}^{\bullet }

{\bar {F}}_{i}^{\text{l,*,RES}}={\bar {F}}_{i}^{\text{l,*}}-{\bar {F}}_{i}^{\bullet ,*}

avec :

${\bar {F}}_{m}^{\text{l,RES}}$ l'énergie libre molaire résiduelle du mélange ;
${\bar {F}}_{i}^{\text{l,*,RES}}$ l'énergie libre molaire résiduelle du corps $i$ pur.

On a donc :

{\bar {F}}_{m}^{\text{E}}={\bar {F}}_{m}^{\text{l,RES}}-\sum _{i=1}^{N}x_{i}{\bar {F}}_{i}^{\text{l,*,RES}}

L'énergie libre molaire d'un mélange liquide s'écrit, avec la forme généralisée (FG2) des équations d'état cubiques :

{\bar {F}}_{m}^{\text{l,RES}}\!\left(P,T,z\right)={\bar {F}}_{m}^{\text{l}}\!\left(P,T,z\right)-{\bar {F}}_{m}^{\bullet }\!\left(P,T,z\right)={a_{m} \over b_{m}}{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},n\right)-RT\,\ln \!\left({P\left({\bar {V}}_{m}^{\text{l}}-b_{m}\right) \over RT}\right)

L'énergie libre molaire résiduelle d'un liquide pur s'écrit, avec la forme généralisée (FG2) des équations d'état cubiques :

{\bar {F}}_{i}^{\text{l,*,RES}}\!\left(P,T\right)={\bar {F}}_{i}^{\text{l,*}}\!\left(P,T\right)-{\bar {F}}_{i}^{\bullet ,*}\!\left(P,T\right)={a_{i} \over b_{i}}{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}}\right)-RT\,\ln \!\left({P\left({\bar {V}}_{i}^{\text{l,*}}-b_{i}\right) \over RT}\right)

En remplaçant les énergies libres résiduelles par leur expression et en réarrangeant on a :

{\bar {F}}_{m}^{\text{E}}={a_{m} \over b_{m}}{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},n\right)-\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}}\right)+\sum _{i=1}^{N}x_{i}RT\,\ln \!\left({{\bar {V}}_{i}^{\text{l,*}}-b_{i} \over {\bar {V}}_{m}^{\text{l}}-b_{m}}\right)

Pour le mélange et le corps pur :

\lim _{P\to +\infty }{\bar {V}}_{m}^{\text{l}}=b_{m}

\lim _{P\to +\infty }{\bar {V}}_{i}^{\text{l,*}}=b_{i}

\lim _{P\to +\infty }{\mathcal {F}}_{m}\!\left({\bar {V}}_{m},z\right)={\mathcal {C}}_{m}

\lim _{P\to +\infty }{\mathcal {F}}_{i}\!\left({\bar {V}}_{i}^{\text{l,*}},z\right)={\mathcal {C}}_{i}

avec :

${\mathcal {C}}_{m}$ la constante ${\mathcal {C}}$ calculée pour le mélange ;
${\mathcal {C}}_{i}$ la constante ${\mathcal {C}}$ calculée pour le corps $i$ pur.

D'où, à pression infinie :

{\bar {F}}_{m}^{\text{E}}\!\left(P=+\infty \right)={a_{m} \over b_{m}}{\mathcal {C}}_{m}-\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{\mathcal {C}}_{i}

Wong et Sandler posent que l'énergie libre est peu sensible à la pression et qu'à basse pression elle est quasi égale à l'enthalpie libre ( $G=F+PV$ , or $PV\ll F$ ), d'où :

{\bar {F}}_{m}^{\text{E}}\!\left(P=+\infty \right)\approx {\bar {F}}_{m}^{\text{E}}\!\left(P\approx 0\right)\approx {\bar {G}}_{m}^{\text{E}}\!\left(P\approx 0\right)

en conséquence :

{a_{m} \over b_{m}}=\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}{{\mathcal {C}}_{i} \over {\mathcal {C}}_{m}}+{{\bar {G}}_{m}^{\text{E}}\!\left(P\approx 0\right) \over {\mathcal {C}}_{m}}

{a_{m} \over b_{m}}=\sum _{i=1}^{N}x_{i}{a_{i} \over b_{i}}+{{\bar {G}}_{m}^{\text{E}}\!\left(P\approx 0\right) \over {\mathcal {C}}}

Cette expression revient à celle de Huron-Vidal, mais il n'a pas été nécessaire d'imposer une règle de mélange sur $b_{m}$ . Pour trouver une deuxième règle de mélange, Wong et Sandler partent du principe que le second coefficient du viriel d'un mélange doit être une forme quadratique de la composition (fractions molaires). En multipliant par ${{\bar {V}} \over RT}$ la forme généralisée (FG2) des équations d'état cubiques, on obtient :

Z={{\bar {V}} \over {\bar {V}}-b}-{{\bar {V}}{a \over RT} \over \left({\bar {V}}-br_{1}\right)\left({\bar {V}}-br_{2}\right)}={{\bar {V}} \over {\bar {V}}-b}-{{\bar {V}}{a \over RT} \over b\left(r_{1}-r_{2}\right)}\left[{1 \over {\bar {V}}-br_{1}}-{1 \over {\bar {V}}-br_{2}}\right]

Z={1 \over 1-{b \over {\bar {V}}}}-{{a \over RT} \over b\left(r_{1}-r_{2}\right)}\left[{1 \over 1-{b \over {\bar {V}}}r_{1}}-{1 \over 1-{b \over {\bar {V}}}r_{2}}\right]

Pour de grands volumes molaires, ${\bar {V}}\gg b$ , soit ${b \over {\bar {V}}}\approx 0$ , on a par développement limité :

{1 \over 1-{b \over {\bar {V}}}}=1+{b \over {\bar {V}}}+{b^{2} \over {\bar {V}}^{2}}+{b^{3} \over {\bar {V}}^{3}}+\cdots

{1 \over 1-{br_{1} \over {\bar {V}}}}=1+{br_{1} \over {\bar {V}}}+{b^{2}{r_{1}}^{2} \over {\bar {V}}^{2}}+{b^{3}{r_{1}}^{3} \over {\bar {V}}^{3}}+\cdots

{1 \over 1-{br_{2} \over {\bar {V}}}}=1+{br_{2} \over {\bar {V}}}+{b^{2}{r_{2}}^{2} \over {\bar {V}}^{2}}+{b^{3}{r_{2}}^{3} \over {\bar {V}}^{3}}+\cdots

On obtient par conséquent un développement sous forme d'équation du viriel :

Z=1+{b \over {\bar {V}}}+{b^{2} \over {\bar {V}}^{2}}+{b^{3} \over {\bar {V}}^{3}}-{{a \over RT} \over b\left(r_{1}-r_{2}\right)}\left[{br_{1} \over {\bar {V}}}+{b^{2}{r_{1}}^{2} \over {\bar {V}}^{2}}+{b^{3}{r_{1}}^{3} \over {\bar {V}}^{3}}-{br_{2} \over {\bar {V}}}-{b^{2}{r_{2}}^{2} \over {\bar {V}}^{2}}-{b^{3}{r_{2}}^{3} \over {\bar {V}}^{3}}\right]+\cdots

=1+{b \over {\bar {V}}}+{b^{2} \over {\bar {V}}^{2}}+{b^{3} \over {\bar {V}}^{3}}-{{a \over RT} \over b\left(r_{1}-r_{2}\right)}\left[{br_{1}-br_{2} \over {\bar {V}}}+{b^{2}{r_{1}}^{2}-b^{2}{r_{2}}^{2} \over {\bar {V}}^{2}}+{b^{3}{r_{1}}^{3}-b^{3}{r_{2}}^{3} \over {\bar {V}}^{3}}\right]+\cdots

En tronquant à l'ordre 2 :

Z=1+\left[b-{a \over RT}\right]{1 \over {\bar {V}}}+\cdots

Le second coefficient du viriel vaut : $B=b-{a \over RT}$ . La thermodynamique statique montre que le second coefficient du viriel d'un mélange est lié aux fractions molaires $x_{i}$ par une relation quadratique :

B_{m}=\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}B_{i,j}

On pose :

B_{i,j}={1 \over 2}\left[B_{i}+B_{j}\right]\left(1-k_{i,j}\right)

avec :

$B_{i}$ le second coefficient du viriel du corps $i$ pur ;
$k_{i,j}$ un paramètre d'interaction binaire entre le corps $i$ et le corps $j$ , tel que $k_{i,j}=k_{j,i}$ et $k_{i,i}=0$ .

On a en conséquence :

\left(b-{a \over RT}\right)_{i,j}={1 \over 2}\left[\left(b_{i}-{a_{i} \over RT}\right)+\left(b_{j}-{a_{j} \over RT}\right)\right]\left(1-k_{i,j}\right)

b_{m}-{a_{m} \over RT}=\sum _{i=1}^{N}\sum _{j=1}^{N}x_{i}x_{j}\left(b-{a \over RT}\right)_{i,j}

Résolution d'une équation d'état cubique

Discriminant r

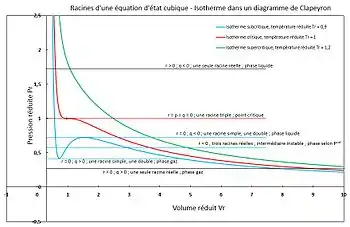
Figure 2 - Racines d'une équation d'état cubique. Signification en fonction de la résolution par la méthode de Cardan.
Sur une isotherme (à température donnée), pour une pression donnée, il peut correspondre une ou plusieurs racines (plusieurs volumes molaires) qui peuvent être attribuées selon le cas à une phase gaz ou une phase liquide.

Soit une équation d'état cubique mise sous sa forme polynomiale généralisée (FP) :

Équation d'état cubique :

Z^{3}+c_{2}Z^{2}+c_{1}Z+c_{0}=0

Le volume molaire ${\bar {V}}$ n'apparait que dans le facteur de compressibilité $Z$ . Connaissant $P$ , $T$ et la composition, le volume molaire du mélange est calculé à partir des racines du polynôme en $Z$ :

{\bar {V}}=Z{RT \over P}

Les racines du polynôme peuvent être trouvées à l'aide de la méthode de Cardan. On pose :

p=c_{1}-{{c_{2}}^{2} \over 3}

q=c_{0}-{c_{1}c_{2} \over 3}+{2{c_{2}}^{3} \over 27}

r=\left({p \over 3}\right)^{3}+\left({q \over 2}\right)^{2}

$r$ est un discriminant qui permet de distinguer trois cas (voir figure 2).

Cas r > 0

Si $r>0$ le polynôme admet une racine réelle et deux complexes, seule la racine réelle nous intéresse :

Z_{0}={\sqrt[{3}]{{-q \over 2}+{\sqrt {r}}}}+{\sqrt[{3}]{{-q \over 2}-{\sqrt {r}}}}-{c_{2} \over 3}

On distingue deux cas :

si $q>0$ le mélange est liquide,
si $q<0$ le mélange est gazeux.

Quelle que soit la température (critique, subcritique ou supercritique), les isothermes possèdent des branches correspondant à $r>0$ . Les isothermes supercritiques ne rencontrent que ce cas.

Cas r = 0

Si $r=0$ le polynôme admet trois racines réelles dont une racine multiple :

si $p=q=0$ alors la racine est triple et $Z_{0}=Z_{1}=Z_{2}=-{c_{2} \over 3}$ , il s'agit du point critique, seule l'isotherme critique rencontre donc ce cas,
sinon, le polynôme admet une racine simple et une double :

racine simple :

Z_{0}=2\cdot {\sqrt[{3}]{-q \over 2}}-{c_{2} \over 3}

racine double :

Z_{1}=Z_{2}=-{\sqrt[{3}]{-q \over 2}}-{c_{2} \over 3}

On distingue deux cas :

si $q>0$ la racine simple correspond à un liquide, la double à un gaz (point K de la figure 1),
si $q<0$ la racine simple correspond à un gaz, la double à un liquide (point I de la figure 1).

Dans les deux cas, la racine double correspond à une phase instable et doit être écartée. Seule la phase correspondant à la racine simple est stable et doit être retenue. Seules les isothermes subcritiques rencontrent le cas

r=0

avec

q\neq 0

Cas r < 0

Si $r<0$ le polynôme admet trois racines réelles distinctes. On pose :

\theta =\arccos \!\left(-{q \over 2}\cdot {\sqrt {-27 \over p^{3}}}\right)

Avec $k\in \left[0,1,2\right]$ , on calcule les trois racines selon :

Z_{k}=2\cdot {\sqrt {-p \over 3}}\cdot \cos \!\left({\theta +2k\pi  \over 3}\right)-{c_{2} \over 3}

La plus grande racine permet de calculer le volume molaire d'un gaz (point G de la figure 1). La plus petite racine permet de calculer le volume molaire d'un liquide (point L de la figure 1). La racine intermédiaire (point J de la figure 1) n'a pas de réalité physique, il s'agirait d'une phase dont le volume molaire augmenterait avec une augmentation de pression (une phase ayant une compressibilité négative), ce qui n'existe pas.

Dans le cas d'un corps pur, si la pression $P>P^{\text{sat}}\!\left(T\right)$ la pression de vapeur saturante, alors seul le liquide est stable. Inversement, si $P<P^{\text{sat}}\!\left(T\right)$ , seul le gaz est stable. Si $P=P^{\text{sat}}\!\left(T\right)$ il y a équilibre liquide-vapeur, les deux phases sont stables. Seules les isothermes subcritiques rencontrent le cas $r<0$ .

Résolution par ordinateur

Lors d'une résolution par ordinateur, les erreurs d'arrondi rendent le cas $r=0$ improbable. De façon générale, si $r$ tend vers 0, c'est-à-dire lorsque $\left({p \over 3}\right)^{3}$ et $\left({q \over 2}\right)^{2}$ sont proches en valeur absolue, mais opposés par le signe, le calcul devient imprécis. Il est alors nécessaire d'affiner les résultats par une autre méthode, comme la méthode de Newton que les résultats de la méthode de Cardan serviraient à initialiser[25] - [26].

Grandeurs calculables avec les équations d'état cubiques

Pression de vapeur saturante

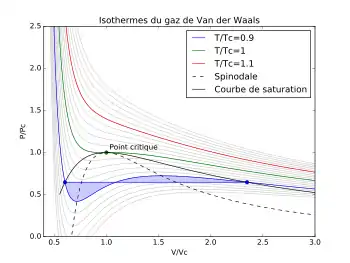
Figure 3 - Règle du palier de Maxwell appliquée à l'équation d'état de Van der Waals : la ligne horizontale est tracée de façon à couper la ligne isotherme théorique en délimitant deux surfaces d'aires égales.

Ce qui suit n'est applicable qu'à un corps pur. Le calcul des pression de bulle et de rosée d'un mélange est plus complexe et nécessite le calcul des coefficients de fugacité de chacun des composants du mélange.

Pour une température $T$ donnée inférieure à la température critique $T_{\mathrm {c} }$ , pour des pressions $P$ inférieures à la pression critique $P_{\mathrm {c} }$ , une équation d'état cubique peut produire trois valeurs du volume molaire ${\bar {V}}$ d'un corps pur : le polynôme de degré trois en $Z=P{\bar {V}}/RT$ peut en effet avoir trois racines réelles. La plus grande de ces racines permet le calcul d'un volume molaire attribuable à un gaz et noté ${\bar {V}}^{\text{g}}$ . La plus petite de ces racines permet de calculer un volume molaire attribuable à un liquide et noté ${\bar {V}}^{\text{l}}$ . La racine intermédiaire n'a pas de sens physique, il s'agirait d'une phase dont le volume molaire augmenterait avec une augmentation de pression (une phase ayant une compressibilité négative), ce qui n'existe pas.

Cependant, une équation d'état cubique suggère pour un corps pur la coexistence des deux phases liquide et gaz sur une certaine plage de pression pour une même température : selon les isothermes bleu turquoise de la figure 1, la coexistence des deux phases serait possible entre les pressions des points I et K. L'expérience toutefois montre que pour un corps pur cette coexistence, ou équilibre, à température $T$ donnée, n'a lieu qu'à une seule pression : la pression de vapeur saturante notée $P^{\text{sat}}\!\left(T\right)$ . Les équations d'état cubiques sont donc incorrectes sur ce point et ne permettent pas le calcul direct des pressions de vapeur saturante, mais la règle du palier de Maxwell remédie à ce problème. Cette règle indique que le gaz et le liquide sont à l'équilibre si :

Règle du palier de Maxwell :

\int _{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}P\,\mathrm {d} {\bar {V}}-P\!\cdot \!\left({\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}\right)=0

Ce qui revient à dire que les deux surfaces violettes représentées sur la figure 3 ci-dessus sont égales.

La forme généralisée (FG2) des équations d'état cubiques donne :

P={RT \over {\bar {V}}-b}-{a \over \left({\bar {V}}-br_{1}\right)\left({\bar {V}}-br_{2}\right)}

\int _{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}P\,\mathrm {d} {\bar {V}}=RT\!\cdot \!\int _{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}{\mathrm {d} {\bar {V}} \over {\bar {V}}-b}-a\!\cdot \!\int _{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}{1 \over \left({\bar {V}}-br_{1}\right)\left({\bar {V}}-br_{2}\right)}\,\mathrm {d} {\bar {V}}

=RT\!\cdot \!{\Biggl [}\ln \!\left({\bar {V}}-b\right){\Biggr ]}_{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}-a\!\cdot \!\left[{{\mathcal {F}}\!\left({\bar {V}}\right) \over b}\right]_{{\bar {V}}^{\text{l}}}^{{\bar {V}}^{\text{g}}}=RT\!\cdot \!\ln \!\left({{\bar {V}}^{\text{g}}-b \over {\bar {V}}^{\text{l}}-b}\right)-{a \over b}\!\cdot \!\left({\mathcal {F}}\!\left({\bar {V}}^{\text{g}}\right)-{\mathcal {F}}\!\left({\bar {V}}^{\text{l}}\right)\right)

On a donc, en appliquant la règle du palier de Maxwell à l'équation d'état cubique généralisée (FG2) :

RT\!\cdot \!\ln \!\left({{\bar {V}}^{\text{g}}-b \over {\bar {V}}^{\text{l}}-b}\right)-{a \over b}\!\cdot \!\left({\mathcal {F}}\!\left({\bar {V}}^{\text{g}}\right)-{\mathcal {F}}\!\left({\bar {V}}^{\text{l}}\right)\right)-P\!\cdot \!\left({\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}\right)=0

La température $T$ étant donnée, on a un système de trois équations à trois inconnues (les volumes molaires ${\bar {V}}^{\text{g}}$ et ${\bar {V}}^{\text{l}}$ et la pression $P^{\text{sat}}$ ) :

P^{\text{sat}}={RT \over {\bar {V}}^{\text{g}}-b}-{a \over \left({\bar {V}}^{\text{g}}-br_{1}\right)\left({\bar {V}}^{\text{g}}-br_{2}\right)}

P^{\text{sat}}={RT \over {\bar {V}}^{\text{l}}-b}-{a \over \left({\bar {V}}^{\text{l}}-br_{1}\right)\left({\bar {V}}^{\text{l}}-br_{2}\right)}

P^{\text{sat}}={RT \over {\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}}\!\cdot \!\ln \!\left({{\bar {V}}^{\text{g}}-b \over {\bar {V}}^{\text{l}}-b}\right)-{a \over b\left({\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}\right)}\left({\mathcal {F}}\!\left({\bar {V}}^{\text{g}}\right)-{\mathcal {F}}\!\left({\bar {V}}^{\text{l}}\right)\right)

Le calcul de la pression de vapeur saturante d'un corps pur à température donnée $T<T_{\mathrm {c} }$ peut s'effectuer de façon itérative comme suit :

fixer la pression $P^{0}<P_{\mathrm {c} }$ ,
calculer la ou les racines de la forme polynomiale cubique de l'équation d'état à $T$ et $P^{0}$ par la méthode de Cardan,
si l'équation ne produit qu'une seule racine réelle, recommencer en 1,
si l'équation produit trois racines réelles, calculer ${\bar {V}}^{\text{g}}$ à partir de la plus grande racine et ${\bar {V}}^{\text{l}}$ à partir de la plus petite racine,
calculer $\Delta =RT\!\cdot \!\ln \!\left({{\bar {V}}^{\text{g}}-b \over {\bar {V}}^{\text{l}}-b}\right)-{a \over b}\!\cdot \!\left({\mathcal {F}}\!\left({\bar {V}}^{\text{g}}\right)-{\mathcal {F}}\!\left({\bar {V}}^{\text{l}}\right)\right)-P\!\cdot \!\left({\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}\right)$ ,
si $\Delta \neq 0$ recommencer en 1,
sinon $P^{\text{sat}}\!\left(T\right)=P^{0}$ .

Une fois la pression de vapeur saturante connue, on peut écarter les phases métastables et instables lorsque l'équation d'état cubique produit trois racines réelles à la même température mais à d'autres pressions que la pression de vapeur saturante. En dessous de $P^{\text{sat}}\!\left(T\right)$ seule la phase gaz existe de façon stable : si l'équation d'état produit trois racines réelles seule celle attribuable à un gaz, la plus grande, doit être retenue. Au-dessus de $P^{\text{sat}}\!\left(T\right)$ seule la phase liquide est stable : si l'équation d'état produit trois racines réelles seule celle attribuable à un liquide, la plus petite, doit être retenue.

Pour un corps pur

Pour un corps pur (liquide ou gazeux) le coefficient de fugacité $\phi ^{*}$ calculé avec la forme généralisée (FG2) des équations d'état cubiques vaut :

Coefficient de fugacité d'un corps pur :

RT\,\ln \phi ^{*}={a \over b}{\mathcal {F}}\!\left({\bar {V}}\right)+P{\bar {V}}-RT-RT\,\ln \!\left({P\left({\bar {V}}-b\right) \over RT}\right)

ou, sous forme adimensionnelle :

\ln \phi ^{*}={A \over B}{\mathcal {F}}\!\left(Z\right)+Z-1-\ln \!\left(Z-B\right)

avec $\phi ^{*}$ le coefficient de fugacité du corps pur.

À saturation, les coefficients de fugacité du corps pur en phases liquide et vapeur sont égaux. On note :

$\phi ^{\text{g,*}}$ le coefficient de fugacité du corps pur en phase gaz ;
$\phi ^{\text{l,*}}$ le coefficient de fugacité du corps pur en phase liquide ;
${\bar {V}}^{\text{g}}$ le volume molaire du corps pur en phase gaz ;
${\bar {V}}^{\text{l}}$ le volume molaire du corps pur en phase liquide.

On a donc, à saturation :

RT\,\ln \phi ^{\text{l,*}}=RT\,\ln \phi ^{\text{g,*}}

{a \over b}{\mathcal {F}}\!\left({\bar {V}}^{\text{l}}\right)+P{\bar {V}}^{\text{l}}-RT-RT\,\ln \!\left({P\left({\bar {V}}^{\text{l}}-b\right) \over RT}\right)={a \over b}{\mathcal {F}}\!\left({\bar {V}}^{\text{g}}\right)+P{\bar {V}}^{\text{g}}-RT-RT\,\ln \!\left({P\left({\bar {V}}^{\text{g}}-b\right) \over RT}\right)

En réarrangeant, on retrouve l'expression issue de la règle du palier de Maxwell appliquée à l'équation d'état cubique généralisée (FG2) :

RT\,\ln \!\left({{\bar {V}}^{\text{g}}-b \over {\bar {V}}^{\text{l}}-b}\right)-{a \over b}\!\cdot \!\left({\mathcal {F}}\!\left({\bar {V}}^{\text{g}}\right)-{\mathcal {F}}\!\left({\bar {V}}^{\text{l}}\right)\right)-P\!\cdot \!\left({\bar {V}}^{\text{g}}-{\bar {V}}^{\text{l}}\right)=0

Pour un corps dans un mélange

Dans ce qui suit un mélange (liquide ou gazeux) de $N$ corps est considéré. Les expressions données ci-dessous sont établies avec la forme généralisée (FG3) des équations d'état cubiques.

Le coefficient de fugacité de tout corps $i$ du mélange est calculé selon :

Coefficient de fugacité d'un corps en mélange :

RT\,\ln \phi _{i}={a+na_{i}^{\prime } \over b}\,RT\,{\mathcal {F}}\!\left({\bar {V}},z\right)+{nb_{i}^{\prime } \over {\bar {V}}-b}RT+P{\bar {V}}-RT-RT\,\ln \!\left({P\left({\bar {V}}-b\right) \over RT}\right)

-{a \over \left(b_{1}-b_{2}\right)}\,RT\,\left[{nb_{1,i}^{\prime }-nb_{2,i}^{\prime } \over b}{\mathcal {F}}\!\left({\bar {V}},z\right)+{nb_{1,i}^{\prime } \over {\bar {V}}+b_{1}}-{nb_{2,i}^{\prime } \over {\bar {V}}+b_{2}}\right]

ou, sous forme adimensionnelle :

\ln \phi _{i}={A+A_{i}^{\prime } \over B}{\mathcal {F}}\!\left(Z,z\right)+{B_{i}^{\prime } \over Z-B}+Z-1-\ln \!\left(Z-B\right)

-{A \over \left(B_{1}-B_{2}\right)}\left[{B_{1,i}^{\prime }-B_{2,i}^{\prime } \over B}{\mathcal {F}}\!\left(Z,z\right)+{B_{1,i}^{\prime } \over Z+B_{1}}-{B_{2,i}^{\prime } \over Z+B_{2}}\right]

avec :

$a_{i}^{\prime }=\left({\partial a \over \partial n_{i}}\right)_{T,n_{j\neq i}}$ la dérivée partielle du terme de cohésion du mélange par rapport à la quantité $n_{i}$ du corps $i$ , à température et quantités des autres corps constantes ;
$A_{i}^{\prime }={na_{i}^{\prime }P \over R^{2}T^{2}}$ le paramètre $a_{i}^{\prime }$ normé ;
$b_{i}^{\prime }=\left({\partial b \over \partial n_{i}}\right)_{T,n_{j\neq i}}$ la dérivée partielle du covolume molaire du mélange par rapport à la quantité $n_{i}$ du corps $i$ , à température et quantités des autres corps constantes ;
$B_{i}^{\prime }={nb_{i}^{\prime }P \over RT}$ le paramètre $b_{i}^{\prime }$ normé ;
$b_{1,i}^{\prime }=\left({\partial b_{1} \over \partial n_{i}}\right)_{T,n_{j\neq i}}$ la dérivée partielle du paramètre $b_{1}$ par rapport à la quantité $n_{i}$ du corps $i$ , à température et quantités des autres corps constantes ;
$B_{1,i}^{\prime }={nb_{1,i}^{\prime }P \over RT}$ le paramètre $b_{1,i}^{\prime }$ normé ;
$b_{2,i}^{\prime }=\left({\partial b_{2} \over \partial n_{i}}\right)_{T,n_{j\neq i}}$ la dérivée partielle du paramètre $b_{2}$ par rapport à la quantité $n_{i}$ du corps $i$ , à température et quantités des autres corps constantes ;
$B_{2,i}^{\prime }={nb_{2,i}^{\prime }P \over RT}$ le paramètre $b_{2,i}^{\prime }$ normé ;
$\phi _{i}$ le coefficient de fugacité du corps $i$ en mélange.

Pour un corps pur $a_{i}^{\prime }=b_{i}^{\prime }=b_{1,i}^{\prime }=b_{2,i}^{\prime }=0$ , on vérifie que l'on retrouve l'expression de $RT\,\ln \phi ^{*}$ .

Grandeurs résiduelles

Les grandeurs résiduelles $X^{\text{RES}}$ expriment l'écart entre les propriétés extensives d'un mélange réel $X$ et celles d'un mélange de gaz parfaits $X^{\bullet }$ . Pour calculer une propriété d'un mélange réel (liquide ou gaz), il suffit donc de calculer la propriété correspondante d'un mélange de gaz parfaits et de lui ajouter la grandeur résiduelle appropriée, toutes ces propriétés étant calculées aux mêmes pression, température et composition que le mélange réel :

Grandeur résiduelle :

X=X^{\bullet }+X^{\text{RES}}

Les grandeurs résiduelles sont calculées avec l'équation d'état cubique généralisée (FG2).

Les expressions données ci-dessous ne sont valables que si seul le paramètre $a$ dépend de la température.

Pour un corps pur comme pour un mélange (liquide ou gazeux), les grandeurs résiduelles valent (les expressions sont données à chaque fois sous forme dimensionnelle et sous forme adimensionnelle) :

énergie libre résiduelle molaire :

{\bar {F}}^{\text{RES}}={a \over b}{\mathcal {F}}\!\left({\bar {V}},z\right)-RT\,\ln \!\left({P\left({\bar {V}}-b\right) \over RT}\right)

{{\bar {F}}^{\text{RES}} \over RT}={A \over B}{\mathcal {F}}\!\left(Z,z\right)-\ln \!\left(Z-B\right)

entropie résiduelle molaire :

{\bar {S}}^{\text{RES}}=-{a_{T}^{\prime } \over b}{\mathcal {F}}\!\left({\bar {V}},z\right)+R\ln \!\left({P\left({\bar {V}}-b\right) \over RT}\right)

{{\bar {S}}^{\text{RES}} \over R}=-{A_{T}^{\prime } \over B}{\mathcal {F}}\!\left(Z,z\right)+\ln \!\left(Z-B\right)

énergie interne résiduelle molaire :

{\bar {U}}^{\text{RES}}={a-Ta_{T}^{\prime } \over b}{\mathcal {F}}\!\left({\bar {V}},z\right)

{{\bar {U}}^{\text{RES}} \over RT}={A-A_{T}^{\prime } \over B}{\mathcal {F}}\!\left(Z,z\right)

volume résiduel molaire :

{\bar {V}}^{\text{RES}}={\bar {V}}-{RT \over P}

{P{\bar {V}}^{\text{RES}} \over RT}=Z-1

enthalpie résiduelle molaire :

{\bar {H}}^{\text{RES}}={a-Ta_{T}^{\prime } \over b}{\mathcal {F}}\!\left({\bar {V}},z\right)+P{\bar {V}}-RT

{{\bar {H}}^{\text{RES}} \over RT}={A-A_{T}^{\prime } \over B}{\mathcal {F}}\!\left(Z,z\right)+Z-1

enthalpie libre résiduelle molaire :

{\bar {G}}^{\text{RES}}={a \over b}{\mathcal {F}}\!\left({\bar {V}},z\right)+P{\bar {V}}-RT-RT\,\ln \!\left({P\left({\bar {V}}-b\right) \over RT}\right)

{{\bar {G}}^{\text{RES}} \over RT}={A \over B}{\mathcal {F}}\!\left(Z,z\right)+Z-1-\ln \!\left(Z-B\right)

avec :

$a_{T}^{\prime }=\left({\partial a \over \partial T}\right)_{n}$ la dérivée partielle du terme de cohésion par rapport à la température à composition constante ;
$A_{T}^{\prime }={a_{T}^{\prime }P \over R^{2}T}$ le paramètre $a_{T}^{\prime }$ normé.

Rappelons que par définition :

pour un corps pur : ${{\bar {G}}^{\text{RES}} \over RT}=\ln \phi ^{*}$ ;
pour un mélange : ${{\bar {G}}^{\text{RES}} \over RT}=\sum _{i=1}^{N}x_{i}\ln \phi _{i}$ .

On remarquera également que pour un gaz parfait (corps pur ou mélange) $A=0$ , $B=0$ et $Z=1$ : toutes les grandeurs résiduelles sont nulles comme il se doit.

Démonstration

Les grandeurs résiduelles sont calculées avec l'équation d'état cubique généralisée (FG2) :

P={nRT \over V-nb}-{n^{2}a \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}

Calculs préalables

Calculons au préalable deux intégrales :

I_{1}=\int _{+\infty }^{V}\left[{1 \over V-nb}-{1 \over V}\right]\,\mathrm {d} V

I_{2}=\int _{+\infty }^{V}{1 \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}\,\mathrm {d} V

Pour la première :

I_{1}=\left[\,\ln \!\left(V-nb\right)-\ln V\,\right]_{+\infty }^{V}=\left[\,\ln \!\left({V-nb \over V}\right)\,\right]_{+\infty }^{V}

En considérant que :

\lim _{V\to \infty }\ln \!\left({V-nb \over V}\right)=\ln 1=0

on a :

I_{1}=\int _{+\infty }^{V}\left[{1 \over V-nb}-{1 \over V}\right]\,\mathrm {d} V=\ln \!\left({V-nb \over V}\right)

Pour la deuxième intégrale, si $r_{1}\neq r_{2}$ on décompose en éléments simples :

{1 \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}={1 \over nb\left(r_{1}-r_{2}\right)}{1 \over V-nbr_{1}}-{1 \over nb\left(r_{1}-r_{2}\right)}{1 \over V-nbr_{2}}

On a donc :

I_{2}={1 \over nb\left(r_{1}-r_{2}\right)}\int _{+\infty }^{V}\left[{1 \over V-nbr_{1}}-{1 \over V-nbr_{2}}\right]\,\mathrm {d} V={1 \over nb\left(r_{1}-r_{2}\right)}\left[\,\ln \!\left(V-nbr_{1}\right)-\ln \!\left(V-nbr_{2}\right)\,\right]_{+\infty }^{V}={1 \over nb\left(r_{1}-r_{2}\right)}\left[\,\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)\,\right]_{+\infty }^{V}

En considérant que :

\lim _{V\to \infty }\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)=\ln 1=0

on a :

I_{2}={1 \over nb\left(r_{1}-r_{2}\right)}\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)

Si $r_{1}=r_{2}$ , y compris si $r_{1}=r_{2}=0$ , on a :

I_{2}=\int _{+\infty }^{V}{1 \over \left(V-nbr_{1}\right)^{2}}\,\mathrm {d} V=\left[\,-{1 \over V-nbr_{1}}\,\right]_{+\infty }^{V}

En considérant que :

\lim _{V\to \infty }{1 \over V-nbr_{1}}=0

on a :

I_{2}=-{1 \over V-nbr_{1}}

On pose la fonction du volume ${\mathcal {F}}$ telle que :

si $r_{1}\neq r_{2}$ : ${\mathcal {F}}\!\left(V,n\right)={1 \over r_{1}-r_{2}}\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)$
si $r_{1}=r_{2}$ (y compris $r_{1}=r_{2}=0$ ) : ${\mathcal {F}}\!\left(V,n\right)=-{nb \over V-nbr_{1}}$

On a par conséquent :

I_{2}=\int _{+\infty }^{V}{1 \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}\,\mathrm {d} V={1 \over nb}{\mathcal {F}}\!\left(V,n\right)

Calcul de l'énergie libre résiduelle molaire

L'énergie libre résiduelle molaire se calcule selon :

n{\bar {F}}^{\text{RES}}=-\int _{+\infty }^{V}\left[P-{nRT \over V}\right]\,\mathrm {d} V-nRT\,\ln Z

On a donc, avec la forme généralisée (FG2) de l'équation d'état cubique :

n{\bar {F}}^{\text{RES}}=-\int _{+\infty }^{V}\left[{nRT \over V-nb}-{n^{2}a \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}-{nRT \over V}\right]\,\mathrm {d} V-nRT\,\ln Z

=-nRT\int _{+\infty }^{V}\left[{1 \over V-nb}-{1 \over V}\right]\,\mathrm {d} V+n^{2}a\int _{+\infty }^{V}{1 \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}\,\mathrm {d} V-nRT\,\ln Z

=-nRTI_{1}+n^{2}aI_{2}-nRT\,\ln Z=-nRT\,\ln \!\left({V-nb \over V}\right)+n{a \over b}{\mathcal {F}}\!\left(V,n\right)-nRT\,\ln Z

Avec par définition :

Z={PV \over nRT}

en réarrangeant on trouve :

{\bar {F}}^{\text{RES}}={a \over b}{\mathcal {F}}\!\left(V,n\right)-RT\,\ln \!\left({P\left(V-nb\right) \over nRT}\right)

Calcul de l'entropie résiduelle molaire

L'entropie résiduelle molaire se calcule selon :

n{\bar {S}}^{\text{RES}}=\int _{+\infty }^{V}\left[\left({\partial P \over \partial T}\right)_{V,n}-{nR \over V}\right]\,\mathrm {d} V+nR\ln Z

On a, avec la forme généralisée (FG2) de l'équation d'état cubique :

\left({\partial P \over \partial T}\right)_{V,n}={nR \over V-nb}-{n^{2}a_{T}^{\prime } \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}

avec $a_{T}^{\prime }=\left({\partial a \over \partial T}\right)_{V,n}$ la dérivée partielle du terme de cohésion par rapport à la température à volume et composition constants, or le paramètre $a$ ne dépend pas du volume : $a_{T}^{\prime }=\left({\partial a \over \partial T}\right)_{n}$ . On suppose ici que seul le paramètre $a$ dépend de la température.

En conséquence :

n{\bar {S}}^{\text{RES}}=\int _{+\infty }^{V}\left[{nR \over V-nb}-{n^{2}a_{T}^{\prime } \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}-{nRT \over V}\right]\,\mathrm {d} V+nR\ln Z

=nR\int _{+\infty }^{V}\left[{1 \over V-nb}-{1 \over V}\right]\,\mathrm {d} V-n^{2}a_{T}^{\prime }\int _{+\infty }^{V}{1 \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}\,\mathrm {d} V+nR\ln Z

=nRI_{1}-n^{2}a_{T}^{\prime }I_{2}+nR\ln Z=nR\ln \!\left({V-nb \over V}\right)-n{a_{T}^{\prime } \over b}{\mathcal {F}}\!\left(V,n\right)+nR\ln Z

Avec par définition :

Z={PV \over nRT}

en réarrangeant on trouve :

{\bar {S}}^{\text{RES}}=-{a_{T}^{\prime } \over b}{\mathcal {F}}\!\left(V,n\right)+R\ln \!\left({P\left(V-nb\right) \over nRT}\right)

Calcul de l'énergie interne résiduelle molaire

Pour l'énergie interne résiduelle molaire, il suffit de considérer la définition :

n{\bar {U}}^{\text{RES}}=n{\bar {F}}^{\text{RES}}+nT{\bar {S}}^{\text{RES}}

Calcul du volume résiduel molaire

Pour le volume résiduel molaire, il suffit de considérer la définition :

n{\bar {V}}^{\text{RES}}=n{\bar {V}}-n{\bar {V}}^{\bullet }

avec ${\bar {V}}^{\bullet }={RT \over P}$ le volume molaire du gaz parfait aux mêmes pression, température et composition que le mélange réel.

Calcul de l'enthalpie résiduelle molaire

Pour l'enthalpie résiduelle molaire, il suffit de considérer la définition :

n{\bar {H}}^{\text{RES}}=n{\bar {U}}^{\text{RES}}+nP{\bar {V}}^{\text{RES}}

Calcul de l'enthalpie libre résiduelle molaire

Pour l'enthalpie libre résiduelle molaire, il suffit de considérer la définition :

n{\bar {G}}^{\text{RES}}=n{\bar {F}}^{\text{RES}}+n{\bar {P}}V^{\text{RES}}

Notations

Alphabet latin

$a$ le terme de cohésion (fonction de la température) ;
$A={aP \over R^{2}T^{2}}$ le terme de cohésion normé ;
$a_{i}$ le paramètre $a$ de l'équation pour le corps $i$ pur ;
$a_{m}$ le paramètre $a$ de l'équation pour un mélange ;
$b$ le covolume molaire (constant) ;
$B={bP \over RT}$ le covolume molaire normé ;
$b_{i}$ le paramètre $b$ de l'équation pour le corps $i$ pur ;
$b_{m}$ le paramètre $b$ de l'équation pour un mélange ;
$b_{1}=-br_{1}$ un paramètre de la forme généralisée (FG3) des équations d'état cubiques ;
$B_{1}={b_{1}P \over RT}$ le paramètre $b_{1}$ normé ;
$b_{2}=-br_{2}$ un paramètre de la forme généralisée (FG3) des équations d'état cubiques ;
$B_{2}={b_{2}P \over RT}$ le paramètre $b_{2}$ normé ;
$c$ un volume molaire correctif (constant) ;
$c_{i}$ le paramètre $c$ de l'équation pour le corps $i$ pur ;
$c_{m}$ le paramètre $c$ de l'équation pour un mélange ;
$c_{2}{,}\,c_{1}{,}\,c_{0}$ les paramètres de la forme généralisée (FP) des équations d'état cubiques ;
$C={cP \over RT}$ le volume molaire correctif normé ;
${\mathcal {C}}$ une constante propre à chaque équation d'état (voir plus bas) ;
${\mathcal {F}}$ une fonction du volume et de la composition (voir plus bas) ;
${\bar {G}}_{\gamma }^{\text{E}}$ un modèle d'enthalpie libre molaire d'excès extérieur à l'équation d'état (comme les modèles de Margules, Van Laar (en), Wilson, NRTL (en), UNIQUAC, UNIFAC ou COSMOSPACE) ;
$k_{i,j}$ un paramètre d'interaction binaire entre le corps $i$ et le corps $j$ , déterminé expérimentalement, avec $k_{i,j}=k_{j,i}$ et $k_{i,i}=0$ ;
${\bar {V}}$ le volume molaire ;
$m$ une fonction du facteur acentrique incluse dans l'expression de $\alpha$ ;
$n$ la quantité de matière (nombre de moles) ;
$N$ le nombre de constituants du mélange ;
$P$ la pression ;
$P_{\mathrm {c} }$ la pression critique d'un corps pur ;
$P^{\text{sat}}$ la pression de vapeur saturante d'un corps pur ;
$r_{1}{,}\,r_{2}$ les paramètres de la forme généralisée (FG2) des équations d'état cubiques ;
$R$ la constante universelle des gaz parfaits ;
$T$ la température absolue ;
$T_{\mathrm {c} }$ la température critique d'un corps pur ;
$T_{\mathrm {r} }$ la température réduite $T_{\mathrm {r} }=T/T_{\mathrm {c} }$ ;
$u$ un paramètre de la forme généralisée (FG1) des équations d'état cubiques ;
$V$ le volume ;
${\bar {V}}$ le volume molaire : ${\bar {V}}=V/n$ ;
${\bar {V}}_{\mathrm {c} }$ le volume molaire critique d'un corps pur ;
${\bar {V}}^{\text{g}}$ le volume molaire d'une phase gaz ;
${\bar {V}}^{\text{l}}$ le volume molaire d'une phase liquide ;
$w$ un paramètre de la forme généralisée (FG1) des équations d'état cubiques ;
$x_{i}$ la fraction molaire du corps $i$ dans un mélange ;
$Z={P{\bar {V}} \over RT}$ le facteur de compressibilité ;
$Z_{\mathrm {c} }={P_{\mathrm {c} }{\bar {V}}_{\mathrm {c} } \over RT_{\mathrm {c} }}$ le facteur de compressibilité critique d'un corps pur.

Alphabet grec

$\alpha$ une fonction de la température réduite $T_{\mathrm {r} }$ , incluse dans l'expression de $a$ ;
$\phi ^{*}$ le coefficient de fugacité d'un corps pur ;
$\phi _{i}$ le coefficient de fugacité du corps $i$ dans un mélange ;
$\omega$ le facteur acentrique.

Constante C et fonction F

${\mathcal {C}}$ est une constante propre à chaque équation d'état définie par :

${\mathcal {C}}={1 \over r_{1}-r_{2}}\ln \!\left({1-r_{1} \over 1-r_{2}}\right)$ avec $r_{1}$ et $r_{2}$ les paramètres de la forme généralisée (FG2) de l'équation d'état cubique ;
si $r_{1}=r_{2}$ (y compris si $r_{1}=r_{2}=0$ ), alors ${\mathcal {C}}=-{1 \over 1-r_{1}}$ .

${\mathcal {F}}$ est une fonction adimensionnelle du volume et de la composition telle que, selon la notation généralisée (FG2) des équations d'état cubiques :

\int _{+\infty }^{V}{1 \over \left(V-nbr_{1}\right)\left(V-nbr_{2}\right)}\,\mathrm {d} V={1 \over nb}{\mathcal {F}}\!\left(V,n\right)

si $r_{1}\neq r_{2}$ : ${\mathcal {F}}\!\left(V,n\right)={1 \over r_{1}-r_{2}}\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)$

On a également, selon la notation :

{\mathcal {F}}\!\left({\bar {V}},z\right)={1 \over r_{1}-r_{2}}\ln \!\left({{\bar {V}}-br_{1} \over {\bar {V}}-br_{2}}\right)=-{b \over b_{1}-b_{2}}\ln \!\left({{\bar {V}}+b_{1} \over {\bar {V}}+b_{2}}\right)

{\mathcal {F}}\!\left(Z,z\right)={1 \over r_{1}-r_{2}}\ln \!\left({Z-Br_{1} \over Z-Br_{2}}\right)=-{B \over B_{1}-B_{2}}\ln \!\left({Z+B_{1} \over Z+B_{2}}\right)

si $r_{1}=r_{2}$ (y compris $r_{1}=r_{2}=0$ ) : ${\mathcal {F}}\!\left(V,n\right)=-{nb \over V-nbr_{1}}$

On a également, selon la notation :

{\mathcal {F}}\!\left({\bar {V}},z\right)=-{b \over {\bar {V}}-br_{1}}=-{b \over {\bar {V}}+b_{1}}

{\mathcal {F}}\!\left(Z,z\right)=-{B \over Z-Br_{1}}=-{B \over Z+B_{1}}

Pour un corps pur

{\mathcal {F}}

est indépendante de la quantité de matière :

{\mathcal {F}}\!\left(V,n\right)={\mathcal {F}}\!\left({\bar {V}}\right)

Remarques sur la fonction

{\mathcal {F}}

et la constante

{\mathcal {C}}

En posant :

{V-nbr_{1} \over V-nbr_{2}}=1+\varepsilon

On a, quel que soit $r_{2}$ , et donc y compris si $r_{2}=0$ :

\varepsilon =-{nb\left(r_{1}-r_{2}\right) \over V-nbr_{2}}

{1 \over r_{1}-r_{2}}=-{nb \over V-nbr_{2}}{1 \over \varepsilon }

{1 \over r_{1}-r_{2}}\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)=-{nb \over V-nbr_{2}}{1 \over \varepsilon }\ln \!\left(1+\varepsilon \right)

En considérant que :

\lim _{r_{1}\to r_{2}}\varepsilon =\lim _{r_{1}\to r_{2}}-{nb\left(r_{1}-r_{2}\right) \over V-nbr_{2}}=0

\lim _{\varepsilon \to 0}{1 \over \varepsilon }\ln \!\left(1+\varepsilon \right)=1

on a la limite :

\lim _{r_{1}\to r_{2}}{1 \over r_{1}-r_{2}}\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)=-{nb \over V-nbr_{2}}\lim _{\varepsilon \to 0}{1 \over \varepsilon }\ln \!\left(1+\varepsilon \right)=-{nb \over V-nbr_{2}}

et puisqu'à la limite $r_{1}=r_{2}$ , y compris si $r_{2}=0$ :

\lim _{r_{1}\to r_{2}}{1 \over r_{1}-r_{2}}\ln \!\left({V-nbr_{1} \over V-nbr_{2}}\right)=-{nb \over V-nbr_{1}}

D'autre part avec la forme généralisée (FG2) des équations d'état cubiques on a :

{\bar {V}}-b={RT \over P}\left[1-{\left({\bar {V}}-b\right){a \over RT} \over \left({\bar {V}}-br_{1}\right)\left({\bar {V}}-br_{2}\right)}\right]

d'où :

\lim _{P\to +\infty }\left[{\bar {V}}-b\right]=0

\lim _{P\to +\infty }{\bar {V}}=b

Pour $r_{1}\neq r_{2}$ :

\lim _{P\to +\infty }{\mathcal {F}}\!\left({\bar {V}},z\right)=\lim _{{\bar {V}}\to b}{1 \over r_{1}-r_{2}}\ln \!\left({{\bar {V}}-br_{1} \over {\bar {V}}-br_{2}}\right)={1 \over r_{1}-r_{2}}\ln \!\left({1-r_{1} \over 1-r_{2}}\right)

pour $r_{1}=r_{2}$ (y compris $r_{1}=r_{2}=0$ ) :

\lim _{P\to +\infty }{\mathcal {F}}\!\left({\bar {V}},z\right)=\lim _{{\bar {V}}\to b}-{b \over {\bar {V}}-br_{1}}=-{1 \over 1-r_{1}}

De façon générale on a donc :

\lim _{P\to +\infty }{\mathcal {F}}\!\left({\bar {V}},z\right)={\mathcal {C}}

Notes et références

Notes

[Corriou (1985)] cite les équations de Onnes, Lee-Edmister, Martin, Usdin-McAuliffe (ou Fuller). [Coquelet et Richon (2007)] cite celles de Fuller (1976), Heyen (1980), Schmidt-Wenzel (1980), Harmens et Knapp (1980), Kubic (1982), Adachi et al. (1983), Trebble-Bishnoi (1987) ; ces équations sont également citées par [Vidal (1997)] pp. 119, 129.
[Vidal (1997)] p. 101.
Par exemple [Privat (2008)].
Extrait de la thèse de Johannes Diderik van der Waals : Over de Continuiteit van den gas- en vloeistoftoestand (De la continuité des états liquides et gazeux), Sijthoff, Leiden (Leyde), 1873.
(en) « For his work on the equation of state for gases and liquids. » in Personnel de rédaction, « The Nobel Prize in Physics 1910 », Fondation Nobel, 2010. Consulté le 17 avril 2016.
R. Clausius, Über das Verhalten der Kohlensäure in Bezug auf Druck, Volumen und Temperatur", Annalen der Physik und Chemie, 9, pp. 337-357, (1880).
R. Clausius, Ueber die theoretische Bestimmung des Dampfdruckes und der Volumina des Dampfes und der Flüssigkeit, Annalen der Physik und Chemie, 14, pp. 279-290, (1881)].
E. Sarrau, Sur la compressibilité des fluides, Comptes Rendus des Séances de l'Académie des Sciences. Paris, 101, pp. 941-944, (1885).
D. J. Berthelot, Sur Une Méthode Purement Physique Pour La Détermination des Poids Moléculaires des Gaz et des Poids Atomiques de Leurs Éléments, J. Phys., 8, pp. 263-274, (1899).
D. Berthelot, Travaux et Mémoires du Bureau international des Poids et Mesures, Tome XIII, Paris : Gauthier-Villars, (1907) lire en ligne sur Gallica.
Antony F. Saturno, Daniel Berthelot's equation of state, Journal of Chemical Education 39(9), pp. 464-465, (1962).
James W. Murdock, Fundamental fluid mechanics for the practicing engineer, CRC Press, 1993, 440 p. (ISBN 0-8247-8808-7), p. 25–27.
(en) Otto Redlich et J.N.S. Kwong, « On The Thermodynamics of Solutions », Chem. Rev., vol. 44, n^o 1,‎ février 1949, p. 233–244 (PMID 18125401, DOI 10.1021/cr60137a013, lire en ligne, consulté le 27 mai 2016).
(en) Giorgio Soave, « Equilibrium constants from a modified Redlich–Kwong equation of state », Chemical Engineering Science, vol. 27, n^o 6,‎ 1972, p. 1197–1203 (DOI 10.1016/0009-2509(72)80096-4, lire en ligne, consulté le 23 mai 2016).
(en) Peng, D. Y. et Robinson, D. B., « A New Two-Constant Equation of State », Industrial and Engineering Chemistry: Fundamentals, vol. 15,‎ 1976, p. 59–64 (DOI 10.1021/i160057a011).
D.B. Robinson, D.Y. Peng, The characterization of the heptanes and heavier fractions for the GPA Peng-Robinson programs, Gas processors association (GPA), Research report RR-28 (1978).
(en) Navin C. Patel et Amin S. Teja, « A New Cubic Equation of State For Fluids and Fluid Mixtures », Chemical Engineering Science, vol. 37, n^o 3,‎ décembre 1982, p. 463–473 (DOI 10.1016/0009-2509(82)80099-7, lire en ligne, consulté le 21 juin 2017).
The Patel Teja cubic equation of state.
(en) José O. Valderrama, « A Generalized Patel-Teja Equation Of State For Polar And Nonpolar Fluids And Their Mixtures », J. Chem. Eng. Jpn., vol. 23, n^o 1,‎ 1990, p. 87-91 (lire en ligne, consulté le 21 juin 2017).
(de) Molekulartheorie eines Korpers, der aus zwei verschiedenen Stoffen besteht (Théorie moléculaire pour un corps composé de deux espèces chimiques différentes), J. D. van der Waals, Zeitschrift fur physikalische Chemie, 5, 133 (1890).
Huron (M.J.) et Vidal (J.), New mixing rules in simple equations of state for representing vapour-liquid equilibria of strongly non ideal mixtures, Fluid Phase Equilib., 3, p. 255-271, Elsevier (1979).
Michelsen (M.L.), A modified Huron-Vidal mixing rule for cubic equations of state, Fluid Phase Equilib. 60, p. 213-219, Elsevier (1990).
Dahl (S.) et Michelsen (M.L.), High pressure vapor-liquid equilibrium with a UNIFAC based equation of state, AlChE J., 36, p. 1829-1836 (1990).
Wong (D.S.H.) et Sandler (S.I.), A theoretically correct mixing rule for cubic equation of state, AlChE. J., 38, p. 671-680 (1992).
(en) Ulrich K. Deiters, « Calculation of Densities from Cubic Equations of State: Revisited », Ind. Eng. Chem. Res., vol. 53, n^o 6,‎ 2014, p. 2529–2536 (DOI 10.1021/ie4038664, lire en ligne, consulté le 21 juin 2017).
(en) Rosendo Monroy-Loperena, « A Note on the Analytical Solution of Cubic Equations of State in Process Simulation », Ind. Eng. Chem. Res., vol. 51, n^o 19,‎ 2012, p. 6972–6976 (DOI 10.1021/ie2023004, lire en ligne, consulté le 21 juin 2017).

Bibliographie

Jean-Pierre Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1026, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et cinétique chimique, pack Opérations unitaires. Génie de la réaction chimique, univers Procédés chimie - bio - agro », 1985, p. 1-30.
Christophe Coquelet et Dominique Richon, Propriétés thermodynamiques : Détermination pour les fluides purs, vol. BE 8030, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et énergétique, pack Physique énergétique, univers : Énergies », 2007, p. 1-8.
Romain Privat, « Développement du modèle PPR78 pour décrire, comprendre et prédire les diagrammes de phases hautes et basses pressions des systèmes binaires et des fluides pétroliers », thèse, université de Lorraine, 2008.
Jean Vidal, Thermodynamique : application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », 1997, 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne).

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.