Facteur de compressibilité

Figure 1 - Isothermes expérimentales de diverses espèces chimiques dans un diagramme d'Amagat.

Figure 2 - Isothermes de l'équation d'état de van der Waals dans un diagramme d'Amagat. Facteur de compressibilité Z en fonction de la pression réduite.
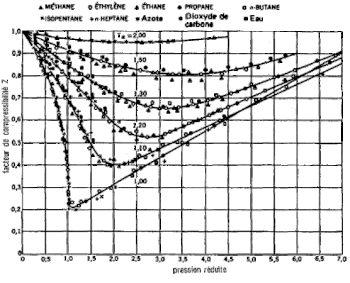
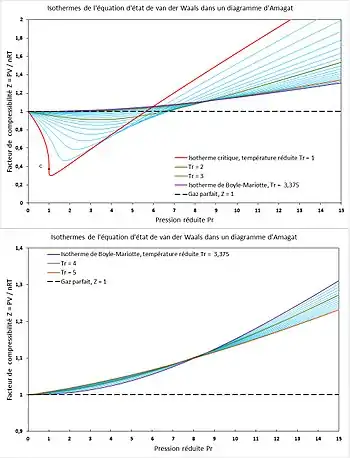
En violet : isotherme de Boyle-Mariotte ; en tirets noirs : droite des gaz parfaits ; en rouge : isotherme critique.

Pour un gaz parfait, le facteur de compressibilité vaut donc 1 quels que soient le gaz (corps pur ou mélange), la pression, la température et la composition. Si l'on trace dans un diagramme le facteur de compressibilité en fonction de la pression, on obtient une unique droite horizontale.

Pour un fluide réel, mélange ou corps pur, le facteur de compressibilité varie généralement entre 0,2 et 1,2 selon la nature du fluide et les conditions opératoires. Pour tracer dans un diagramme le facteur de compressibilité d'un fluide réel en fonction de la pression, on fixe la température et la composition pour obtenir une courbe isotherme. La variation de la température permet d'obtenir un faisceau de courbes isothermes. La figure 1 montre les isothermes obtenues expérimentalement pour diverses espèces chimiques et tracées dans un diagramme d'Amagat. La figure 2 montre dans un diagramme d'Amagat l'évolution isotherme du facteur de compressibilité d'un gaz suivant l'équation d'état de van der Waals, qui représente qualitativement[2] le comportement d'un gaz réel. On constate :
1- qu'à basse pression ou à haute température le facteur de compressibilité d'un fluide réel tend vers 1 : le comportement d'un fluide réel tend vers celui d'un gaz parfait ;
2- qu'à pression constante :

• aux basses pressions le facteur de compressibilité augmente avec la température ;
• aux hautes pressions le facteur de compressibilité diminue avec une augmentation de température ;

3- qu'à température constante :

• le facteur de compressibilité est décroissant aux basses pressions et croissant aux hautes pressions ;
• au-delà d'une certaine température le facteur de compressibilité est strictement croissant.

Au point critique, le facteur de compressibilité d'un gaz de van der Waals vaut ${\displaystyle Z_{\mathrm {c} }=0{,}375}$ quel que soit le corps, ce qui n'est pas réaliste. En règle générale, le facteur de compressibilité critique d'un corps réel vaut de 0,2 à 0,3[3]. On a par exemple respectivement pour l'hydrogène, l'éthane, l'ammoniac et l'eau : ${\displaystyle Z_{\mathrm {c} }({\rm {H_{2}}})=0{,}304}$, ${\displaystyle Z_{\mathrm {c} }({\rm {C_{2}H_{6}}})=0{,}267}$, ${\displaystyle Z_{\mathrm {c} }({\rm {NH_{3}}})=0{,}238}$, ${\displaystyle Z_{\mathrm {c} }({\rm {H_{2}O}})=0{,}226}$.

Par définition, un gaz parfait est un gaz dans lequel des particules ponctuelles n'ont aucune interaction entre elles, si ce n'est des chocs élastiques. Autrement dit, dans un gaz parfait les particules n'ont aucune interaction à distance entre elles, contrairement aux fluides réels dans lesquels les particules interagissent à distance par les forces de van der Waals. Ainsi :

• si ${\displaystyle Z<1}$, le volume du fluide réel est inférieur à celui du gaz parfait correspondant, les forces d'attraction entre particules l'emportent sur les forces de répulsion ;
• si ${\displaystyle Z>1}$, le volume du fluide réel est supérieur à celui du gaz parfait correspondant, les forces de répulsion entre particules l'emportent sur les forces d'attraction ;
• si ${\displaystyle Z=1}$, le fluide se comporte comme un gaz parfait, les forces d'attraction et de répulsion entre particules s'annulent mutuellement.

Figure 3 - Isothermes de l'équation d'état de van der Waals dans un diagramme d'Amagat. Produit de la pression réduite par le volume réduit en fonction de la pression réduite.
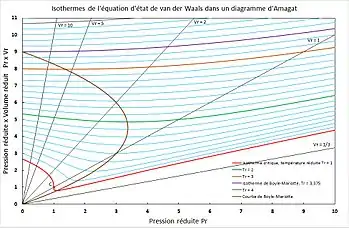
En marron : courbe de Boyle-Mariotte ; en violet : isotherme de Boyle-Mariotte ; en rouge : isotherme critique.

En dérivant le facteur de compressibilité par rapport à la pression, à température et quantité de matière constantes :

${\displaystyle \left({\partial Z \over \partial P}\right)_{T,n}={1 \over nRT}\left({\partial PV \over \partial P}\right)_{T,n}={P \over nRT}\left({\partial V \over \partial P}\right)_{T,n}+{V \over nRT}}$

en introduisant le coefficient de compressibilité isotherme ${\displaystyle \chi _{T}=-{1 \over V}\left({\partial V \over \partial P}\right)_{T,n}}$ et en remarquant que pour un gaz parfait ${\displaystyle \chi _{T}^{\bullet }={1 \over P}}$, on obtient :

Variation isotherme : ${\displaystyle \left({\partial Z \over \partial P}\right)_{T,n}=-{Z \over P}\left({\chi _{T} \over \chi _{T}^{\bullet }}-1\right)}$

Il s'agit de la pente des isothermes tracées dans le diagramme d'Amagat ci-dessus :

• lorsque cette pente est négative, le fluide est plus compressible que le gaz parfait correspondant : ${\displaystyle \chi _{T}>\chi _{T}^{\bullet }}$ ; lors d'une compression les forces d'attraction entre molécules l'emportent sur les forces de répulsion et favorisent la compression ; ceci s'observe dans les gaz à basse pression ;
• inversement, lorsque cette pente est positive, le fluide est moins compressible que le gaz parfait correspondant : ${\displaystyle \chi _{T}<\chi _{T}^{\bullet }}$ ; lors d'une compression les forces de répulsion entre molécules l'emportent sur les forces d'attraction et s'opposent à la compression ; ceci s'observe dans les gaz à haute pression et les liquides ;
• lorsque cette pente est nulle, le fluide a la même compressibilité que le gaz parfait correspondant : ${\displaystyle \chi _{T}=\chi _{T}^{\bullet }={1 \over P}}$ ; les forces d'attraction et de répulsion entre molécules se compensent lors de la compression ; dans le diagramme d'Amagat, les points correspondants sont les points auxquels la tangente à l'isotherme est une droite horizontale.

Pour un gaz parfait, selon la loi de Boyle-Mariotte, à température et quantité de matière constantes, ${\displaystyle PV={\text{constante}}}$, soit ${\displaystyle \left({\partial PV \over \partial P}\right)_{T,n}=0}$. Pour un fluide réel, le lieu des points des isothermes du diagramme d'Amagat de tangente horizontale (appelés points de Boyle-Mariotte) est appelé courbe de Boyle-Mariotte[4]. En effet, en tout point de tangente horizontale dans le diagramme d'Amagat, ${\displaystyle \left({\partial Z \over \partial P}\right)_{T,n}=0}$ équivaut à ${\displaystyle \left({\partial PV \over \partial P}\right)_{T,n}=0}$.

Il existe une température, appelée température de Boyle-Mariotte, au-delà de laquelle les isothermes dans le diagramme d'Amagat n'ont plus de point de tangente horizontale et sont strictement croissantes. L'isotherme correspondante est appelée isotherme de Boyle-Mariotte. La courbe et l'isotherme de Boyle-Mariotte sont représentées sur la figure 3 pour un gaz de van der Waals.

En utilisant la relation :

${\displaystyle \left({\partial Z \over \partial V}\right)_{T,n}=\left({\partial Z \over \partial P}\right)_{T,n}\left({\partial P \over \partial V}\right)_{T,n}}$

on obtient :

Variation isotherme : ${\displaystyle \left({\partial Z \over \partial V}\right)_{T,n}=-{Z \over V}\left({K \over K^{\bullet }}-1\right)}$

avec :

• ${\displaystyle K=-V\left({\partial P \over \partial V}\right)_{T,n}=1/\chi _{T}}$ le module d'élasticité isostatique du corps réel ;
• ${\displaystyle K^{\bullet }=1/\chi _{T}^{\bullet }=P}$ le module d'élasticité isostatique du gaz parfait.

En dérivant le facteur de compressibilité par rapport à la température, à pression et quantité de matière constantes :

${\displaystyle \left({\partial Z \over \partial T}\right)_{P,n}={P \over nR}\left({\partial \over \partial T}{V \over T}\right)_{P,n}={P \over nRT}\left({\partial V \over \partial T}\right)_{P,n}-{PV \over nRT^{2}}}$

en introduisant le coefficient de dilatation isobare ${\displaystyle \alpha ={1 \over V}\left({\partial V \over \partial T}\right)_{P,n}}$ et en remarquant que pour un gaz parfait ${\displaystyle \alpha ^{\bullet }={1 \over T}}$, on obtient :

Variation isobare : ${\displaystyle \left({\partial Z \over \partial T}\right)_{P,n}={Z \over T}\left({\alpha \over \alpha ^{\bullet }}-1\right)}$

Ainsi :

• si ${\displaystyle \alpha >\alpha ^{\bullet }}$, alors ${\displaystyle Z}$ est croissant avec la température à pression constante, ce qui est le cas des gaz à basse pression ;
• si ${\displaystyle \alpha <\alpha ^{\bullet }}$, alors ${\displaystyle Z}$ est décroissant avec une température croissante à pression constante, ce qui est le cas des gaz à haute pression ;
• si ${\displaystyle \alpha =\alpha ^{\bullet }={1 \over T}}$, alors ${\displaystyle \left({\partial Z \over \partial T}\right)_{P,n}=0}$, équivalant à ${\displaystyle \left({\partial \over \partial T}{V \over T}\right)_{P,n}=0}$ : en ces points le gaz suit la loi de Charles des gaz parfaits.

En dérivant le facteur de compressibilité par rapport à la température, à volume et quantité de matière constants :

${\displaystyle \left({\partial Z \over \partial T}\right)_{V,n}={V \over nR}\left({\partial \over \partial T}{P \over T}\right)_{V,n}={V \over nRT}\left({\partial P \over \partial T}\right)_{V,n}-{PV \over nRT^{2}}}$

en introduisant le coefficient de compression isochore ${\displaystyle \beta ={1 \over P}\left({\partial P \over \partial T}\right)_{V,n}}$ et en remarquant que pour un gaz parfait ${\displaystyle \beta ^{\bullet }={1 \over T}}$, on obtient :

Variation isochore : ${\displaystyle \left({\partial Z \over \partial T}\right)_{V,n}={Z \over T}\left({\beta \over \beta ^{\bullet }}-1\right)}$

Ainsi :

• si ${\displaystyle \beta >\beta ^{\bullet }}$, alors ${\displaystyle Z}$ est croissant avec la température à volume constant ;
• si ${\displaystyle \beta <\beta ^{\bullet }}$, alors ${\displaystyle Z}$ est décroissant avec une température croissante à volume constant ;
• si ${\displaystyle \beta =\beta ^{\bullet }={1 \over T}}$, alors ${\displaystyle \left({\partial Z \over \partial T}\right)_{V,n}=0}$, équivalant à ${\displaystyle \left({\partial \over \partial T}{P \over T}\right)_{V,n}=0}$ : en ces points le gaz suit la loi de Gay-Lussac des gaz parfaits.

Soit un mélange de quantité de matière globale ${\displaystyle n=\sum _{i}n_{i}}$ avec ${\displaystyle n_{i}}$ la quantité du constituant ${\displaystyle i}$.

En dérivant le facteur de compressibilité par rapport à la quantité de matière globale ${\displaystyle n}$ à pression, température et fractions molaires ${\displaystyle z_{i}=n_{i}/n}$ des constituants constantes :

${\displaystyle \left({\partial Z \over \partial n}\right)_{P,T,z}={P \over RT}\left({\partial \over \partial n}{V \over n}\right)_{P,T,z}}$

en introduisant le volume molaire ${\displaystyle {\bar {V}}=V/n}$ et en remarquant que celui-ci ne dépend que de la pression, de la température et des fractions molaires, mais pas de la quantité de matière globale, soit ${\displaystyle {\bar {V}}=V\!\left(P,T,z\right)}$ et ${\displaystyle \left({\partial {\bar {V}} \over \partial n}\right)_{P,T,z}=0}$, on obtient :

Variation selon la quantité de matière totale : ${\displaystyle \left({\partial Z \over \partial n}\right)_{P,T,z}=0}$

Le facteur de compressibilité étant une grandeur intensive, il ne dépend pas de la quantité globale de matière du mélange.

En dérivant le facteur de compressibilité par rapport à la quantité de l'un des constituants ${\displaystyle i}$ du mélange, à pression, température et quantités des autres constituants constantes :

${\displaystyle \left({\partial Z \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}={P \over RT}\left({\partial \over \partial n_{i}}{V \over n}\right)_{P,T,n_{j\neq i}}={P \over nRT}\left({\partial V \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}-{PV \over n^{2}RT}}$

en introduisant le volume molaire partiel ${\displaystyle {\bar {V}}_{i}=\left({\partial V \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}}$ du constituant ${\displaystyle i}$ et le volume molaire ${\displaystyle {\bar {V}}=V/n}$ du mélange réel, on obtient :

Variation selon la quantité d'un constituant : ${\displaystyle \left({\partial Z \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}={Z \over n}\left({{\bar {V}}_{i} \over {\bar {V}}}-1\right)}$

Ainsi :

• si ${\displaystyle {\bar {V}}_{i}>{\bar {V}}}$, alors ${\displaystyle Z}$ est croissant avec la quantité de ${\displaystyle i}$ croissante à pression et température constantes ;
• si ${\displaystyle {\bar {V}}_{i}<{\bar {V}}}$, alors ${\displaystyle Z}$ est décroissant avec la quantité de ${\displaystyle i}$ croissante à pression et température constantes ;
• si ${\displaystyle {\bar {V}}_{i}={\bar {V}}}$, alors ${\displaystyle \left({\partial Z \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}=0}$ : en ces points le gaz suit la loi d'Avogadro des gaz parfaits, pour lesquels ${\displaystyle {\bar {V}}_{i}={\bar {V}}}$.

Si l'on connait le facteur de compressibilité d'un corps (tabulé dans la littérature, voir par exemple la table donnée pour l'air plus bas), le volume molaire de ce corps (pur ou mélange, liquide ou gaz) se calcule selon :

${\displaystyle {\bar {V}}=Z{RT \over P}}$

Puisque la masse volumique ${\displaystyle \rho }$ se calcule selon :

${\displaystyle \rho ={M \over {\bar {V}}}}$

avec ${\displaystyle M}$ la masse molaire du corps, on a :

Masse volumique : ${\displaystyle \rho ={1 \over Z}{PM \over RT}}$

où ${\displaystyle \rho ^{\bullet }={PM \over RT}}$ est la masse volumique du gaz parfait correspondant au corps réel (mêmes pression, température et composition).

Unités

Selon le Système international d'unités la pression est exprimée en Pa et la température en K. La masse molaire est généralement exprimée en g/mol (ou kg/kmol). La masse volumique calculée selon la formule ci-dessus est ainsi obtenue en g/m³ et doit être divisée par 1000 pour obtenir des kg/m³.

Le facteur de compressibilité est souvent utilisé comme variable dans les équations d'état[5], par exemple dans les diverses formes d'équation du viriel :

${\displaystyle Z=1+{B_{2} \over {\bar {V}}}+{B_{3} \over {\bar {V}}^{2}}+{B_{4} \over {\bar {V}}^{3}}+\cdots }$

${\displaystyle Z=1+C_{2}\cdot P+C_{3}\cdot P^{2}+C_{4}\cdot P^{3}+\cdots }$

ou dans les équations d'état cubiques, comme celles de van der Waals et de Redlich-Kwong :

${\displaystyle Z^{3}+c_{2}Z^{2}+c_{1}Z+c_{0}=0}$

ou encore dans les équations de Benedict–Webb–Rubin et de Lee-Kesler.

La loi des gaz parfaits revient à ${\displaystyle Z=1}$.

Le coefficient de fugacité ${\displaystyle \phi _{i}}$ est défini par le rapport de la fugacité ${\displaystyle f_{i}}$ d'un corps ${\displaystyle i}$, pur ou dans un mélange, à la pression partielle de ce corps dans le mélange, soit ${\displaystyle z_{i}P}$ avec ${\displaystyle z_{i}}$ la fraction molaire du corps ${\displaystyle i}$ : ${\displaystyle \phi _{i}={f_{i} \over z_{i}P}}$. La pression partielle du corps ${\displaystyle i}$ est la fugacité de ce corps dans le mélange de gaz parfaits de mêmes pression, température et composition que le mélange réel. Pour un corps ${\displaystyle i}$, pur ou dans un mélange, le coefficient de fugacité ${\displaystyle \phi _{i}}$ peut se calculer :

• avec une équation d'état dans laquelle le volume ${\displaystyle V}$ est exprimé explicitement en fonction de la pression ${\displaystyle P}$, de la température ${\displaystyle T}$ et de la composition (nombre de moles ${\displaystyle n_{i}}$ de chacun des constituants du mélange), ${\displaystyle V=V\!\left(P,T,n\right)}$, comme l'une des formes de l'équation du viriel, selon :

${\displaystyle \ln \phi _{i}=\int _{0}^{P}\left[n\left({\partial Z \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}+Z-1\right]{\mathrm {d} P \over P}}$

• avec une équation d'état dans laquelle la pression ${\displaystyle P}$ est exprimée explicitement en fonction du volume ${\displaystyle V}$, de la température ${\displaystyle T}$ et de la composition (nombre de moles ${\displaystyle n_{i}}$ de chacun des constituants du mélange), ${\displaystyle P=P\!\left(V,T,n\right)}$, telle que les équations d'état cubiques, selon :

${\displaystyle \ln \phi _{i}=-\int _{+\infty }^{V}\left[n\left({\partial Z \over \partial n_{i}}\right)_{V,T,n_{j\neq i}}+Z-1\right]{\mathrm {d} V \over V}-\ln Z}$

avec :

• ${\displaystyle \left({\partial Z \over \partial n_{i}}\right)_{P,T,n_{j\neq i}}}$ la dérivée partielle du facteur de compressibilité par rapport à la quantité du corps ${\displaystyle i}$, à pression, température et quantités des corps ${\displaystyle j}$ autres que ${\displaystyle i}$ constants ;
• ${\displaystyle \left({\partial Z \over \partial n_{i}}\right)_{V,T,n_{j\neq i}}}$ la dérivée partielle du facteur de compressibilité par rapport à la quantité du corps ${\displaystyle i}$, à volume, température et quantités des corps ${\displaystyle j}$ autres que ${\displaystyle i}$ constants ;
• ${\displaystyle n_{i}}$ le nombre de moles du corps ${\displaystyle i}$ dans le mélange ;
• ${\displaystyle n=\sum _{i=1}^{N}n_{i}}$ la quantité de matière totale (nombre de moles total) dans le mélange.

Pour un gaz parfait ${\displaystyle Z^{\bullet }=1}$, d'où ${\displaystyle \ln \phi _{i}^{\bullet }=0}$ et ${\displaystyle \phi _{i}^{\bullet }=1}$.

Une grandeur résiduelle ${\displaystyle X^{\text{RES}}}$ exprime l'écart entre une propriété extensive ${\displaystyle X}$ d'un fluide réel et la même propriété ${\displaystyle X^{\bullet }}$ d'un gaz parfait dans les mêmes conditions de pression, température et composition que le fluide réel : ${\displaystyle X^{\text{RES}}=X-X^{\bullet }}$. Pour un corps pur ou un mélange, les grandeurs résiduelles peuvent se calculer :

• avec une équation d'état dans laquelle le volume ${\displaystyle V}$ est exprimé explicitement en fonction de la pression ${\displaystyle P}$, de la température ${\displaystyle T}$ et de la composition (nombre de moles ${\displaystyle n_{i}}$ de chacun des constituants du mélange), ${\displaystyle V=V\!\left(P,T,n\right)}$, comme l'une des formes de l'équation du viriel, selon :
  • enthalpie libre molaire résiduelle :

  ${\displaystyle {{\bar {G}}^{\text{RES}} \over RT}=\int _{0}^{P}\left[Z-1\right]{\mathrm {d} P \over P}}$

  • entropie molaire résiduelle :

  ${\displaystyle {{\bar {S}}^{\text{RES}} \over R}=-\int _{0}^{P}\left[T\left({\partial Z \over \partial T}\right)_{P,n}+Z-1\right]{\mathrm {d} P \over P}}$

  • enthalpie molaire résiduelle :

  ${\displaystyle {{\bar {H}}^{\text{RES}} \over RT}=-\int _{0}^{P}\left[T\left({\partial Z \over \partial T}\right)_{P,n}\right]{\mathrm {d} P \over P}}$

  • volume molaire résiduel :

  ${\displaystyle Z^{\text{RES}}={P{\bar {V}}^{\text{RES}} \over RT}=Z-1}$

  • énergie interne molaire résiduelle :

  ${\displaystyle {{\bar {U}}^{\text{RES}} \over RT}=-\int _{0}^{P}\left[T\left({\partial Z \over \partial T}\right)_{P,n}\right]{\mathrm {d} P \over P}-Z+1}$

  • énergie libre molaire résiduelle :

  ${\displaystyle {{\bar {F}}^{\text{RES}} \over RT}=\int _{0}^{P}\left[Z-1\right]{\mathrm {d} P \over P}-Z+1}$

• avec une équation d'état dans laquelle la pression ${\displaystyle P}$ est exprimée explicitement en fonction du volume ${\displaystyle V}$, de la température ${\displaystyle T}$ et de la composition (nombre de moles ${\displaystyle n_{i}}$ de chacun des constituants du mélange), ${\displaystyle P=P\!\left(V,T,n\right)}$, telle que les équations d'état cubiques, selon :
  • énergie libre molaire résiduelle :

  ${\displaystyle {{\bar {F}}^{\text{RES}} \over RT}=-\int _{+\infty }^{V}\left[Z-1\right]\,{\mathrm {d} V \over V}-\ln Z}$

  • entropie molaire résiduelle :

  ${\displaystyle {{\bar {S}}^{\text{RES}} \over R}=\int _{+\infty }^{V}\left[T\left({\partial Z \over \partial T}\right)_{V,n}+Z-1\right]\,{\mathrm {d} V \over V}+\ln Z}$

  • énergie interne molaire résiduelle :

  ${\displaystyle {{\bar {U}}^{\text{RES}} \over RT}=\int _{+\infty }^{V}\left[T\left({\partial Z \over \partial T}\right)_{V,n}\right]{\mathrm {d} V \over V}}$

  • volume molaire résiduel :

  ${\displaystyle Z^{\text{RES}}={P{\bar {V}}^{\text{RES}} \over RT}=Z-1}$

  • enthalpie molaire résiduelle :

  ${\displaystyle {{\bar {H}}^{\text{RES}} \over RT}=\int _{+\infty }^{V}\left[T\left({\partial Z \over \partial T}\right)_{V,n}\right]{\mathrm {d} V \over V}+Z-1}$

  • enthalpie libre molaire résiduelle :

  ${\displaystyle {{\bar {G}}^{\text{RES}} \over RT}=-\int _{+\infty }^{V}\left[Z-1\right]\,{\mathrm {d} V \over V}+Z-1-\ln Z}$

avec :

• ${\displaystyle \left({\partial Z \over \partial T}\right)_{P,n}}$ la dérivée partielle du facteur de compressibilité par rapport à la température du mélange, à pression et quantités de tous les constituants du mélange constantes ;
• ${\displaystyle \left({\partial Z \over \partial T}\right)_{V,n}}$ la dérivée partielle du facteur de compressibilité par rapport à la température du mélange, à volume et quantités de tous les constituants du mélange constants.

Pour un gaz parfait ${\displaystyle Z^{\bullet }=1}$, toutes les grandeurs résiduelles sont nulles.

• Jean Vidal, Thermodynamique : application au génie chimique et à l'industrie pétrolière, Paris, Éditions Technip, coll. « Publications de l'Institut français du pétrole. », 1997, 500 p. (ISBN 978-2-7108-0715-5, OCLC 300489419, lire en ligne).
• Christophe Coquelet et Dominique Richon, Propriétés thermodynamiques : Détermination pour les fluides purs, vol. BE 8030, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et énergétique, pack Physique énergétique, univers : Énergies », 2007, p. 1-8.
• Jean-Pierre Corriou, Thermodynamique chimique : Diagrammes thermodynamiques, vol. J 1026, Techniques de l'ingénieur, coll. « base documentaire Thermodynamique et cinétique chimique, pack Opérations unitaires. Génie de la réaction chimique, univers Procédés chimie - bio - agro », 1985, p. 1-30.
• Roland Solimando, Louis Schuffenecker et Jean-Noël Jaubert, Propriétés thermodynamiques du corps pur, Techniques de l'ingénieur (n^o AF 050), 2000 (lire en ligne), p. 8.

• Coefficients calorimétriques et thermoélastiques
• Diagramme d'Amagat
• Équation d'état cubique
• Loi des états correspondants