UNIQUAC
UNIQUAC (abréviation de Universal QUAsiChemical) est un modèle de coefficient d'activité utilisé dans la description des équilibres entre phases[1]. Le modèle est aussi appelé le modèle du treillage et est un prolongement qui vient d’une approximation de premier ordre de l'interaction des surfaces moléculaires en statistiques thermodynamiques. Le modèle n'est cependant pas entièrement compatible thermodynamiquement en raison de sa théorie sur les deux mélanges liquides. Dans cette approche, la concentration locale autour d’une molécule centrale est supposée être indépendante de la composition locale autour d'un autre type de molécule.
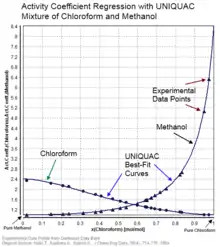
Il a été démontré que, malgré le fait que les compositions locales soient corrélées, ignorer cette corrélation a un effet négligeable sur la corrélation des coefficients d'activité[2]. Aujourd'hui, le modèle UNIQUAC est fréquemment utilisé dans la description des équilibres de phases (c'est-à-dire : liquide-solide, liquide-liquide ou équilibre liquide-vapeur). Le modèle UNIQUAC sert aussi de base au développement à la méthode de contribution groupée UNIFAC, où les molécules sont subdivisées en groupes atomiques. En effet, UNIQUAC est égal à UNIFAC pour les mélanges de molécules, qui ne sont pas subdivisés ; par exemple le système binaire eau-méthanol, du méthanol et du formaldéhyde-acrylonitrile-DMF.
Une forme thermodynamiquement plus cohérente d’UNIQUAC est proposée par le modèle plus récent: COSMOSPACE, et le modèle équivalent GEQUAC[3].
Les équations
Dans le modèle UNIQUAC, les coefficients d'activité de la ith composante d'un mélange à deux composants, sont décrits par un combinatoire et une contribution résiduelle.
Le premier est un terme entropique qui quantifie l'écart par rapport à la solubilité idéale comme le résultat de différences dans la forme des molécules. Celui-ci est une correction enthalpique[nb 1] due à la variation dans l'interaction des forces entre des molécules différentes lors du mélange.
Contribution combinatoire
Les comptes de contribution combinatoires des formes différencie les molécules, affecte l'entropie du mélange et s'appuie sur la théorie des treillis. L’excès d'entropie γC est calculé exclusivement à partir des paramètres chimiques purs, en utilisant le rapport de Van der Waals sur les volumes ri et les aires de surfaces[nb 2] des produits chimiques purs.
Avec la fraction du volume par la fraction molaire du mélange, Vi, pour la composante ith est donnée par :
Et la fraction de l’aire superficielle par la fraction molaire du mélange, Fi, pour la composante ith est donnée par :
Les 3 premiers termes du côté droit du combinatoire forment la contribution de Flory-Huggins, tandis que les termes de gauche, la correction de Guggenhem-Staverman, les réduisent parce que des segments de liaison ne peuvent pas être placés dans toutes les directions dans l’espace. Cette correction spatiale décale le résultat de l'expression de Flory-Huggins d’environ 5 % par rapport à une solution idéale. Le nombre de coordination, z, c'est-à-dire le nombre de molécules en interaction étroites autour d'une molécule centrale, est souvent fixé à 10. Elle peut être considérée comme une valeur moyenne qui se situe entre cube (z = 6) et l'emballage hexagonal (z = 12) des molécules qui sont simplifiés par des sphères.
Dans la limite de la dilution infinie et d'un mélange binaire, les équations de la contribution combinatoire se réduit à :
Cette paire d’équation montre que les molécules de même forme, à savoir les mêmes paramètres r et q, ont
La contribution résiduelle
La durée de vie résiduelle contient un paramètre empirique , qui est un dérivé des coefficients d’activité estimés occasionnellement ou de manière expérimentale. L'expression du coefficient d'activité résiduel pour la molécule i est :
avec
Δuij [J/mol]est le paramètre d’énergie d'interaction binaire. La théorie définit Δuij = uij – uii, et Δuji = uji – ujj, où uij est l'énergie d'interaction entre les molécules i et j.
Habituellement Δuij ≠ Δuji, parce que les énergies d'évaporation (c’est-à-dire uii), sont dans de nombreux cas différents, alors que l'énergie d'interaction entre la molécule i et j est symétrique, et donc uij=uji. Si les interactions entre les molécules j et i sont les mêmes que celles entre les molécules i et j, et que le mélange n'a pas d'effet d’excès sur l'énergie lors du mélange, alors Δuij=Δuji=0. Et c'est ainsi que
Alternativement, dans certains logiciels de simulation de procédés, peut être exprimé comme suit :
Les coefficients "C", "D" et "E" sont principalement utilisés dans le raccord équilibres liquide-liquide (avec "D" et "E" rarement utilisé à cela). Le "C" coefficient est utile dans les équilibres liquide-vapeur ainsi. L'utilisation d'une telle expression ne tient pas compte du fait que sur le plan de l'énergie moléculaire, Δuij, est indépendante de la température. Il s'agit d'une correction de réparer les simplifications qui ont été appliquées dans la dérivation du modèle.
Applications
Les coefficients d'activité peuvent être utilisés pour prédire les équilibres de phase simples (vapeur-liquide, liquide-liquide, solide-liquide), ou d'estimer d'autres propriétés physiques (par exemple la viscosité des mélanges). Des modèles tels que UNIQUAC permettent aux ingénieurs chimiques de prédire le comportement de phase des mélanges chimiques à composants multiples. Ils sont couramment utilisés dans les programmes de simulation de phénomènes pour calculer le bilan massique dans et autour des unités de séparation.
Paramètres
UNIQUAC nécessite deux paramètres fondamentaux sous-jacents :
- La surface relative et les fractions volumiques sont des constantes chimiques, qui doivent être connues pour tous les produits chimiques.
- Un paramètre empirique entre les composantes qui décrit le comportement intermoléculaire. Ce paramètre doit être connu pour toutes les paires binaires dans le mélange. Dans un mélange quaternaire, il y a six paramètres (tels que 1-2,1-3,1-4,2-3,2-4,3-4) et le nombre augmente rapidement avec d'autres composantes chimiques. Les paramètres empiriques sont dérivés à partir de coefficients d'activité d'expérimentation ou de diagrammes de phase, à partir desquels les coefficients d'activité eux-mêmes peuvent être calculés. Une alternative est d'obtenir les coefficients d'activité avec une méthode comme UNIFAC ; alors, les paramètres UNIFAC peuvent être simplifiés en essayant pour obtenir les paramètres UNIQUAC. Cette méthode permet le calcul plus rapide des coefficients d'activité, plutôt que l'utilisation directe de la méthode plus complexe.
Les nouveaux développements
UNIQUAC a été prolongée par plusieurs groupes de recherche. Certains dérivés sélectionnés sont :
- (en)UNIFAC: un procédé qui permet d’estimer le volume, la surface et, en particulier, les paramètres d'interactions binaires. Cela permet d'éliminer l'utilisation de données expérimentales pour calculer les paramètres UNIQUAC.
- Les extensions pour l'estimation des coefficients d'activité pour les mélanges électrolytiques[4].
- Les extensions pour mieux décrire la dépendance des coefficients d'activité par la température[4].
- Des solutions pour des arrangements moléculaires[5].
Notes et références
Notes
- Dans cet article, on suppose que la variation d'enthalpie lors du mélange peut être considérée comme étant égale à l'énergie lors du mélange, alors l’excès de liquide du volume molaire est de petite taille et Hex = Δ + ΔUex Vex AP ≈ ΔU
- qiIci, on suppose que toutes les molécules ont la même indice de coordination du groupe méthylène d'un alcane, qui est la référence pour calculer le volume relatif et la surface.
Références
- Abrams DS, Prausnitz JM, "Thermodynamique statistique des mélanges liquides: une nouvelle expression de l'excès d'énergie de Gibbs de systèmes partiellement ou totalement miscibles", AIChE J., 21 (1), 116-128, 1975
- McDermott (Équilibre des phases fluides 1 (1977) 33) et Flemr (Coll.Czech.Chem.Comm., 41 (1976) 3347)
- Egner, K., Gaube, J., et Pfennig, A.: GEQUAC, un modèle d’excès d’énergie de GIBBS pour la description simultanée de l'association et de la non-association des mélanges liquides. Ber. Buns. Ges. 101 (2): 209-218 (1997). Egner, K., Gaube, J., et Pfennig, A.: GEQUAC, un modèle d’excès d’énergie de GIBBS décrivant l'association et non-association de mélanges liquides par un nouveau modèle conceptuel pour les groupes fonctionnels. Équilibre des phases fluides 158-160: 381-389 (1999)
- Ab Wisniewska-Goclowska B., Malanowski SK, "Une nouvelle modification de l'équation UNIQUAC comprenant les paramètres dépendants de la température», Équilibre des phases fluides 180, 103-113, 2001
- Andreas Klamt, Gerard JP Krooshof, Ross Taylor "COSMOSPACE: Alternative aux modèles classiques sur les coefficients activité", AIChE J., 48 (10), 2332-2349,2004
Voir aussi
Articles connexes
Liens externes
- (fr)MOSCED: un modèle pour estimer la limitation des coefficients d'activité à dilution infinie.
- (en)NRTL, Non-Random Two Liquid Model : une alternative à UNIQUAC du même type de composition locale.










