Visualisation de données
La visualisation des données (ou dataviz ou représentation graphique de données) est un ensemble de méthodes permettant de résumer de manière graphique des données statistiques qualitatives et surtout quantitatives afin de montrer les liens entre des ensembles de ces données. Cette visualisation (en) fait partie de la science des données.
| Partie de |
Visualisation (en) |
|---|---|
| Personnes clés |
La visualisation de données naît au XVIIIe siècle, avec les travaux de Charles-René de Fourcroy et notamment de William Playfair. Elle se développe très largement au XIXe siècle avec l'invention des cartes de données dans les années 1820 et 1830 par Charles Dupin ou André-Michel Guerry, les travaux de Florence Nightingale et dans le second XIXe siècle avec les travaux de Charles Joseph Minard (1781-1870)[1] - [2] - [3], Francis Amasa Walker ou encore Émile Cheysson. Enfin, elle se prend un nouvel essor à partir du second XXe siècle sous l'impulsion de John Tukey qui met en avant le rôle de la visualisation en statistique puis d'Edward Tufte et enfin avec le développement du numérique.
La visualisation de données est notamment utilisée dans la statistique publique, dans les sciences, dans le journalisme et plus particulièrement dans le journalisme de données et plus généralement en science des données.
Histoire
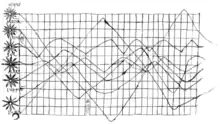
La visualisation des données remonte à la mise en liste et la mise en tableau, dont on trouve trace dès l'apparition de l'écriture (cf. Jack Goody, La raison graphique, 1979).
La création d'objets graphiques complexes apparait plus tardivement. Les premiers sont des cartes géographiques ou astronomiques[5] - [6] dont on pense que la première remonte au VIIe millénaire avant notre ère.
On trouve des frises chronologiques chez les premiers astronomes, au Xe siècle dans le Commentaire au songe de Scipion de Macrobe, par exemple.

Puis, au XVIIIe siècle, des auteurs comme Charles-René de Fourcroy proposent des illustrations abstraites tel le « Tableau poléométrique » (1782) qui permet la comparaison instantanée de la taille de villes européennes, ou August Friedrich Wilhelm Crome avec sa « Verhaeltniss Karte von den deutschen Bundesstaaten » (1785) qui permet la comparaison de la taille des pays. En 1786, William Playfair (1759-1823) publie un ouvrage intitulé The Commercial and Political Atlas qui fait date. Il y propose une série de graphiques de séries temporelles représentant l'évolution de données économiques concernant l'Angleterre et notamment l'évolution de sa balance commerciale au cours du XVIIIe siècle, ainsi que le premier diagramme en bâtons de l'histoire[7] - [8] - [9]. C'est aussi à William Playfair que l'on doit le premier graphique circulaire connu. Publié en 1801 dans The Statistical Breviary, le graphique représente la superficie, le montant des revenus et le montant des taxes de chaque pays[8].
En 1819 l'historien Jean Picot publie à Genève un volume intitulé Statistique de la Suisse ou État de ce pays et des vingt-deux cantons dont il se compose […]. Il contient sur un feuillet dépliant deux graphiques d'après les données de Johannes Fehr : « Étendue ou surface comparative des vingt-deux Cantons de la Suisse représentée par la longueur des lignes tracées à côté du nom de chaque canton » et « Population comparative des vingt-deux Cantons de la Suisse représentée par la longueur des lignes tracées à côté du nom de chaque canton ».
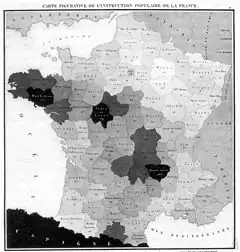

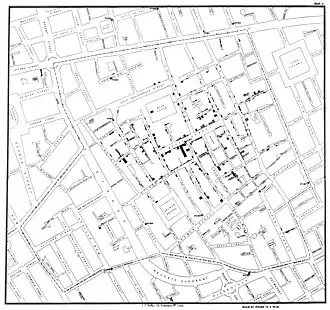
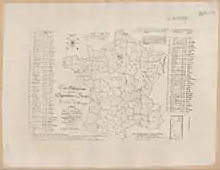
Dans les années 1820, on commence à représenter des données statistiques sur une carte. En 1826, Charles Dupin dessine une carte choroplèthe de l'instruction populaire en France, en coloriant les départements français en fonction de l'intensité de la variable représentée. Cette représentation visuelle rencontre un rapide succès et est aussitôt reprise par André-Michel Guerry et Adriano Balbi qui dessinent des cartes choroplèthes de l'instruction, du nombre de crimes contre les propriétés et du nombre de crimes contre les personnes puis par Guerry dans son Essai sur la statistique morale de la France publié en 1833[10]. Peu de temps après, Armand Joseph Frère de Montizon propose la première « cartes par points » (dot map), avec une représentation de la population française par département intitulée Carte Philosophique figurant la Population de la France[12]. En 1855, le médecin britannique John Snow établit une carte de points du choléra à Londres sur laquelle il représente la localisation des morts et la localisation des points d'eau dans la ville de Londres mettant ainsi en évidence le fait que l'épidémie se propage par l'eau[13]. En 1861, Charles Joseph Minard propose de représenter des données sur une carte à l'aide de diagrammes circulaires dont l'aire est proportionnelle à la quantité représentée (Exemple de la Carte figurative et approximative des quantités de viandes de boucherie envoyées sur pied par les départements et consommateurs)[14].

En 1857, Florence Nightingale publie son Diagramme des causes de mortalité au sein de l'armée en Orient. Le graphique montre que les soldats anglais engagés dans la guerre de Crimée meurent moins au combat face à l'ennemi qu'ils ne sont victimes des conditions sanitaires déplorables dans lesquelles ils vivent[14].
En 1889 Charles Booth combine approche ethnographique à grande échelle et visualisation sous forme cartographique, pour rendre compte des conditions de vie à Londres. Cette étude sociologique, une des plus importantes du genre, a mobilisé une équipe d'enquêteurs rémunérés par Booth afin de collecter des données au niveau de chaque parcelle cadastrale. La visualisation proposée par Booth détaille, par des couleurs, 7 "classes". La visualisation permet d'identifier des clusters, notamment pour la classe la plus basse que Booth dénomme « classe inférieure. Vicieux, semi-criminel »[15].
Au cours de la seconde moitié du XIXe siècle, on découvre plusieurs innovations importantes, comme les premières visualisations en trois dimensions de l'Italien Luigi Perozzo ou de l'Allemand Gustav Zeuner[14].
_modeled_on_actual_data_(Swedish_census%252C_1750-1875).jpg.webp)
Au Royaume-Uni, c'est Francis Galton qui fait une importante contribution à la visualisation de données en proposant des représentations graphiques de la corrélation entre deux variables (nuage de points) mais aussi des cartes météorologiques[16].
Au cours du premier XXe siècle, les statisticiens prêtent une moindre attention à la visualisation de données[17].
Dans les années 1960, John Tukey donne ses lettres de noblesse à la visualisation de données en statistiques, notamment avec son ouvrage Exploratory Data Analysis (1977)[18].
En 2005, Leland Wilkinson publie The Grammar of Graphics, un des ouvrages théoriques les plus importants sur la conception des graphiques statistiques. Wilkinson définit un graphique statistique comme une correspondance entre des données et des attributs esthétiques (couleur, forme, taille, etc) d'objets géométriques (points, lignes, barres, etc.)[19].
Structure d'une visualisation
Une visualisation est composée d'un élément visuel, d'une échelle, d'un système de coordonnées et d'un contexte[20].
Dans un nuage de points, on utilise la position des points dans l'espace comme élément visuel représentant les données[20]. Dans un diagramme en bâtons, c'est la longueur des barres qui est l'élément visuel correspondant aux données[21].
Le système de coordonnées peut être cartésien, polaire ou géographique[22].
L'échelle peut être linéaire ou logarithmique lorsqu'il s'agit d'une variable quantitative, catégorique lorsqu'il s'agit d'une variable catégorique ou temporelle lorsqu'il s'agit du temps[23].
Typologie en fonction des formes représentées
Diagramme en bâtons
Ce type de diagramme est aussi appelé diagramme à barres.
Pour un diagramme en bâtons vertical, on représente pour chaque modalité d'une variable discrète un rectangle dont la hauteur représente la valeur d'une variable continue et dont la largeur n'a pas d'interprétation statistique.
Pour un diagramme en bâtons horizontal, c'est la largeur du rectangle qui représente la valeur de la variable continue et la hauteur de ce rectangle qui n'a pas d'interprétation statistique[24].
Il est aussi courant de rencontrer des diagrammes en bâtons empilés (en anglais : stacked bar chart).
- Exemples de diagrammes en bâton
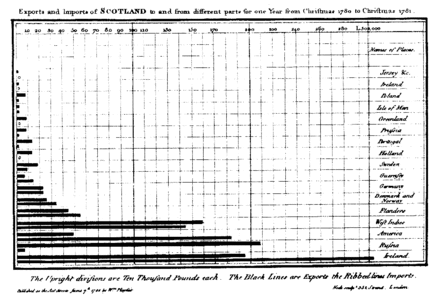 Les imports et les exports de l'Écosse entre noël 1780 et noël 1781. C'est le premier diagramme en bâtons de l'histoire. Il a été publié par William Playfair dans son ouvrage The Commercial and Political Atlas (1786).
Les imports et les exports de l'Écosse entre noël 1780 et noël 1781. C'est le premier diagramme en bâtons de l'histoire. Il a été publié par William Playfair dans son ouvrage The Commercial and Political Atlas (1786).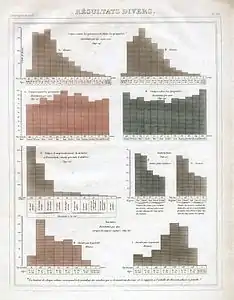 Diagrammes en bâtons dans l'Essai sur la statistique morale de la France d'André-Michel Guerry, Planche VII, 1833
Diagrammes en bâtons dans l'Essai sur la statistique morale de la France d'André-Michel Guerry, Planche VII, 1833
Diagramme branche-et-feuille
Le diagramme branche-et-feuille livre une représentation semi-graphique des données quantitatives, semblable à un histogramme.
Diagramme circulaire
Le diagramme circulaire peut être un graphique à secteurs[25] — dit camembert — ou un graphique en anneau[25] (donut chart en anglais).
Le diagramme circulaire ou camembert permet de représenter des proportions. C'est l'angle de chaque secteur qui représente la part de chaque catégorie dans un tout[26].
Le graphique en anneau(x) (donut chart en anglais) est un camembert troué au milieu. Il permet de représenter plusieurs séries de données en anneaux concentriques, une série par anneau[25].
Lorsque le graphique ne compte qu'un seul anneau, la longueur de l'arc de cercle correspondant à chaque catégorie est proportionnelle à l'angle et représente encore la part de chaque catégorie dans le tout représenté[27].
« Le graphique en anneau est une bonne représentation des données du tableau. Comme pour le graphique en secteurs, il nécessite la transformation préalable des données en proportions. On peut toutefois faire figurer sur les segments de l'anneau les valeurs en milliers. Ceci étant, s'il n'y a qu'un seul anneau, autant choisir un graphique en secteurs. »
— Centre national de documentation pédagogique[28]
- Exemple de diagramme circulaire
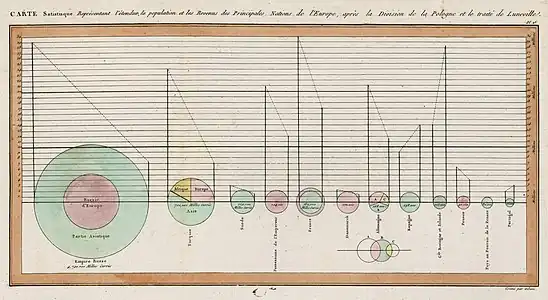 Diagrammes circulaires publiés par William Playfair dans The Statistical Breviary (1801). Les cercles représentent la superficie de chaque pays. Les lignes à gauche de chaque cercle représentent la population (en millions d'habitants) et les lignes à droite représentent le total des taxes collectées (en millions de livres sterling). La ligne pointillée met en relation la ligne des revenus et la ligne des taxes. Sa pente n'a pas d'interprétation mais le signe de la pente en a une. Le graphique montre qu'en Grande-Bretagne, le total des taxes comparé à la population est plus élevé que dans les autres pays[29].
Diagrammes circulaires publiés par William Playfair dans The Statistical Breviary (1801). Les cercles représentent la superficie de chaque pays. Les lignes à gauche de chaque cercle représentent la population (en millions d'habitants) et les lignes à droite représentent le total des taxes collectées (en millions de livres sterling). La ligne pointillée met en relation la ligne des revenus et la ligne des taxes. Sa pente n'a pas d'interprétation mais le signe de la pente en a une. Le graphique montre qu'en Grande-Bretagne, le total des taxes comparé à la population est plus élevé que dans les autres pays[29].
Nuage de points
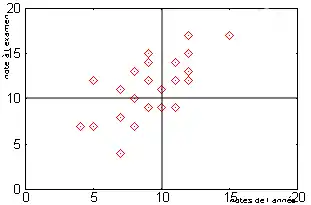
Le nuage de points est couramment utilisé pour représenter la relation entre deux variables. Dans un nuage de points, ce sont les coordonnées de chaque point sur l'axe des abscisses et l'axe des ordonnées qui représentent les valeurs de chacune des variables[30]. Il permet de mettre en évidence une corrélation entre deux variables[31].
Ligne
Une ligne ou line plot est un nuage de points dans lequel les points ont été reliés entre eux (avec une interpolation qui peut être linéaire, cubique...)[32].
Diagramme à bulles
On peut aussi représenter graphiquement des données quantitatives grâce à des bulles dans lequel la surface des bulles est proportionnelle à la grandeur représentée[33].
Carte thermique (heatmap)

Une carte thermique (heatmap, carte de chaleur) est une matrice dont les cellules sont colorées en fonction de la valeur de la variable représentée[35].
Boîte à moustaches
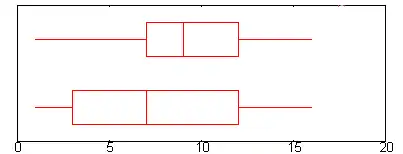
Le diagramme en boîte à moustaches résume seulement quelques caractéristiques de position du caractère étudié (médiane, quartiles, min/max ou déciles). Il est utilisé principalement pour comparer un même caractère dans deux populations de tailles différentes.
Il s'agit de tracer un rectangle allant du premier quartile au troisième quartile et coupé par la médiane. On ajoute parfois des segments aux extrémités menant jusqu'aux valeurs min/max ou jusqu'au premier et neuvième décile. On parle alors de diagramme en boîte à moustaches ou à pattes.
Mini-graphes (sparklines)
Les mini-graphes, mini-courbes et mini-indicateurs[36] sont des graphiques de petite taille (environ une ligne de hauteur), qui peuvent être insérés dans une ligne de texte. Ils sont popularisés par Edward Tufte, qui les définit comme des « graphiques intenses en données, de design simple, et ayant la taille d’un mot ». Alors que le graphique typique est conçu de manière à montrer le plus de données possible et qu'il est placé hors-texte, les mini-graphes sont concis, mémorisables visuellement, et placés à l’endroit le plus approprié. Leur mise à disposition dans les tableurs de suite logicielle connue les a rendu populaires.
| Sparklines
Marché américain des actions (7 février 2006) | ||
|---|---|---|
| Jour | Indice | Valeur |
| Dow Jones | −32.82 (−0,30 %) | |
| S&P 500 | −8.10 (−0,64 %) | |
| Nasdaq | −13.97 (−0,62 %) | |
Typologie selon le type de données représentées
Visualisation de données temporelles
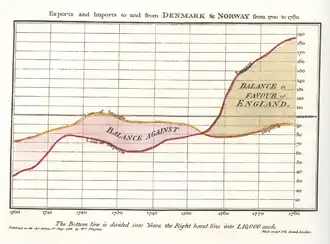
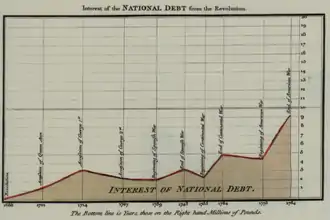
Le graphique de série temporelle représente l'évolution d'une variable en fonction du temps. C'est la représentation graphique la plus utilisée et son interprétation est généralement très intuitive.
Si la série temporelle est discrète, il est courant d'utiliser un simple diagramme en bâtons pour la représenter. Par exemple, les données annuelles ou mensuelles sont souvent représentées par des diagrammes en bâtons. En revanche, si les données sont continues, il est plus courant de les représenter par une courbe (line plot) ou un graphique d'aire (area chart), comme l'avait fait William Playfair dans son Commercial and Political Atlas (voir ici et ici)[37].
Visualisation de données géolocalisées
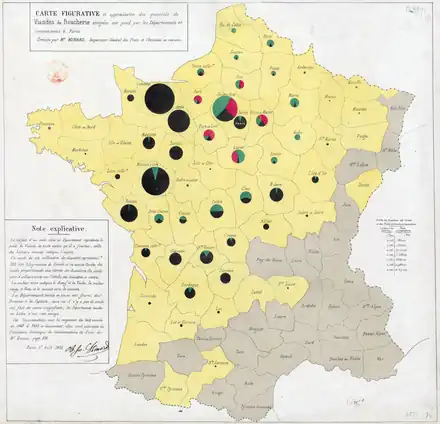
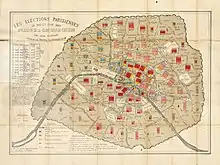
Une carte statistique permet de représenter la valeur d'une variable statistique dans chacune des unités géographiques d'une entité globale. La carte statistique a l'avantage de pouvoir à la fois révéler une analyse globale tout en permettant à chacun d'aller repérer des détails pour chaque unité géographique. En revanche, elle a le défaut de donner à chaque unité géographique une importance proportionnelle à sa superficie alors que dans de nombreuses situations il serait préférable que l'importance que l'on donne à chaque unité géographique soit relative à une autre variable, comme sa population par exemple[38] - [note 1].
Si les cartes géographiques ont été inventées il y a plus de 5 000 ans, les cartes statistiques sont apparues au XVIIe siècle. En 1686, Edmond Halley représente une carte du monde avec des symboles permettant de donner l'origine et surtout l'intensité des vents. Plus tard, au XIXe siècle, John Snow représente une carte de Londres en localisant le nombre de morts dus au choléra lors de l'épidémie de septembre 1854 et les points d'accès à l'eau dans la ville. Sa carte permet de comprendre que le choléra se transmet par l'eau[39].
Visualisation de la relation entre plusieurs variables
Pour représenter la relation entre deux variables, il est courant d'utiliser un nuage de points[31].
Lorsqu'il y a plus de deux variables, il existe de nombreuses solutions. La solution la plus simple consiste à représenter une matrice de nuages de points[40]. On peut aussi utiliser un graphique de bulles dans lequel, comme dans un nuage de points, les coordonnées des bulles représentent les valeurs de deux variables et dans lequel la surface des bulles représente une troisième variable[33].
Iconographie des corrélations
Lorsqu’il a de nombreuses variables, l’iconographie des corrélations remplace la matrice de corrélation par une image unique : les corrélations « remarquables » sont soulignées par un trait plein (corrélation positive) ou pointillé (corrélation négative).
Une forte corrélation n’est pas « remarquable » si elle n’est pas directe, mais causée par l’effet d’une tierce variable. Inversement de faibles corrélations peuvent être « remarquables ». Par exemple, si une variable Y dépend de plusieurs variables indépendantes, les corrélations de Y avec chacune d’entre elles sont faibles et pourtant « remarquables ».
Visualisation d'une distribution statistique
Dans le cas discret, il est courant d'utiliser un diagramme à barres où la hauteur de chaque rectangle représente les effectifs ou les fréquences associées à chaque modalité.
Visualisation d'une arborescence
Lorsque les données ont une structure hiérarchique, elles peuvent être représentées sous la forme d'un dendrogramme, d'une treemap ou encore d'un sunburst[41].
Carte à cases (treemap)
La carte à cases est une représentation visuelle inventée par Ben Shneiderman en 1990 pour représenter l'occupation de l'espace sur son disque dur. Dans cette représentation, c'est la surface de chaque rectangle qui représente la part de chaque élément dans le tout[42]. Par la suite, cette représentation a été utilisée pour d'autres usages. Par exemple, Martin Wattenberg l'a utilisée pour représenter une « carte du marché » par secteur d'activité dans laquelle la surface de chaque rectangle est proportionnelle à la capitalisation boursière des entreprises du secteur[43]. Marcos Westamp a conçu une carte à cases de l'information dans laquelle la taille des rectangles est une fonction du nombre d'articles consacrés au sujet dans la presse[44] - [45]. Matthew Bloch, Shan Carter et Amanda Cox, ont utilisé une carte à cases pour visualiser la part de chaque type de bien dans la consommation d'un ménage américain et un code couleur pour visualiser l'inflation[46] - [47].
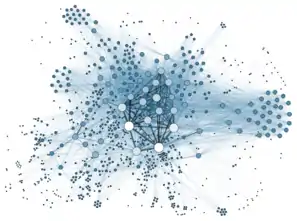
Visualisation de réseaux
Filippo Menczer (Université d'Indiana) est le premier à mettre au jour l'activité d'un bot sur Twitter en 2010 par le biais d'une visualisation de réseaux[48]. L'analyse de réseaux est aujourd'hui utilisé pour visualiser la formation des bulles de filtres.
Visualisation de flux
Le diagramme de flux est un type de représentation spécifique pour visualiser des flux.
Représentation des effectifs cumulés
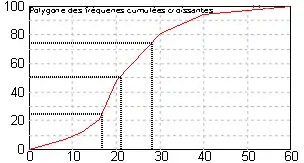
Pour les variables continues, on peut tracer le polygone des effectifs (ou fréquences) cumulés. Le principe du tracé est expliqué dans l'article statistiques élémentaires continues. Ce polygone, permet de lire très rapidement l'effectif d'un intervalle de la forme et, par différence, l'effectif de tout intervalle. Elle permet aussi de lire très rapidement les quartiles et les déciles. Cette représentation préfigure le tracé de la fonction de répartition en probabilité.
On voit apparaître parfois un polygone des effectifs cumulés pour des variables discrètes. En toute rigueur, il faudrait tracer un diagramme en escalier.
Bibliographie
- (en) William Playfair, The Commercial and Political Atlas : Representing, by Means of Stained Copper-Plate Charts, the Progress of the Commerce, Revenues, Expenditure and Debts of England during the Whole of the Eighteenth Century,
- (en) William Playfair, Statistical Breviary : Shewing, on a Principle Entirely New, the Resources of Every State and Kingdom in Europe, Londres, Wallis, , 1re éd.
- André-Michel Guerry, Essai sur la statistique morale de la France, Crochard,
- (en) Howard G. Funkhouser (en), Historical Development of the Graphical Representation of Statistical Data, Saint Catherine Press,
- Jacques Bertin, Sémiologie graphique : Les diagrammes, les réseaux, les cartes, Paris, Presses de l'EHESS,
- (en) John Tukey, Exploratory Data Analysis, Addison-Wesley Publishing Company,
- (en) Edward Tufte, The Visual Display of Quantitative Information, Graphics Press USA, , 2e éd. (1re éd. 1983), 190 p.
- (en) Stephen Fienberg, « Graphical methods in statistics », The American Statistician, vol. 33, no 4, , p. 165-178
- (en) William Cleveland, Visualizing Data, At&T Bell Laboratories, , 360 p.
- G. Palsky, Des chiffres et des cartes : naissance et développement de la cartographie quantitative française au XIXe siècle, Comité des travaux historiques et scientifiques-CTHS,
- (en) Leland Wilkinson, The Grammar of Graphics, Springer, coll. « Statistics and Computing », , 2e éd., 691 p. (ISBN 978-0-387-24544-7, lire en ligne)
- (en) Forrest W. Young, Pedro M. Valero-Mora et Michael Friendly, Visual Statistics : Seeing Data with Dynamic Interactive Graphics, , 400 p. (ISBN 978-0-471-68160-1)
- (en) Chun-Houh Chen (dir.), Wolfgang Hardle (dir.), Antony Unwin (dir.) et al., Handbook of Data Visualization, Springer-Verlag, coll. « Springer Handbooks of Computational Statistics », , 936 p. (ISBN 978-3-540-33036-3)
- (en) Nathan Yau (en), Visualize This : The FlowingData Guide to Design, Visualization, and Statistics, Indianapolis, Ind., John Wiley & Sons, , 384 p. (ISBN 978-0-470-94488-2)
- Bernard Lebelle, Convaincre avec des graphiques efficaces, Edition d'Organisation,
- (en) Alberto Cairo (en), The Functional Art : An introduction to information graphics and visualization, New Riders, coll. « Voices That Matter », , 363 p. (ISBN 978-0-321-83473-7)
- (en) Nathan Yau, Data Points : Visualization That Means Something, John Wiley & Sons, , 336 p. (ISBN 978-1-118-46219-5, lire en ligne)
- Jean-Marie Lagnel, Manuel de datavisualisation, Éditions Dunod, , 2e éd.
- (en) Michael Friendly et Howard Wainer, A History of Data Visualization and Graphic Communication, Harvard University Press, , 288 p. (ISBN 9780674975231 et 0674975235)
Vidéographie
- (en) Geoff McGhee, Journalism in the Age of Data, voir en ligne
- (en) David McCandless, La beauté de la visualisation des données, voir en ligne
Expositions
- 2018 : 1,2,3 data, Fondation EDF à Paris[50]
- 2020 : Data Visualization and the Modern Imagination, exposition en ligne à la bibliothèque de l'université Stanford[51]
Notes et références
- Cet article est partiellement ou en totalité issu de l'article intitulé « Représentation graphique de données » (voir la liste des auteurs).
Notes
- Edward Tufte parle de « data maps », littéralement « cartes de données »
Références
- Victorin Chevallier, « Notice nécrologique sur M. Minard, inspecteur général des ponts et chaussées, en retraite », Annales des ponts et chaussées : Mémoires et documents, Paris, Dunod, vol. II de la 5e série, 2e sem. 1871, p. 1–22
- « Biographie de Charles Joseph Minard »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le ) sur 19e.org, site consacré à l'histoire du XIXe siècle.
- Charles Joseph Minard: Mapping Napoleon's March, 1861 by John Corbett, Center for Spatially Integrated Social Science.
- (en) Michael Friendly, « A Brief History of Data Visualization », dans Handbook of Data Visualization, (DOI 10.1007/978-3-540-33037-0_2), p. 19.
- (en) Michael Friendly, « Milestones in the history of thematic cartography, statistical graphics, and data visualization »,
- « Milestones: Section 2. Pre-1600 », sur euclid.psych.yorku.ca (consulté le )
- Tufte 2001, p. 9.
- Friendly 2008, p. 9-10.
- Tufte 2001, p. 33.
- Friendly 2008, p. 39.
- Adriano Balbi et André-Michel Guerry, Statistique comparée de l'état de l'instruction et du nombre des crimes dans les divers arrondissements des académies et des cours royales de France, Paris, Jules Renouard,
- Jean-Paul Bord (dir.) et Pierre-Robert Baduel (dir.), Les cartes de la connaissance, Khartala, , p. 593
- Friendly 2008, p. 27.
- Friendly 2008, p. 30.
- « Cette étude de marché a 120 ans et combine Big Data et qualitatif », sur Conseils en marketing, (consulté le )
- Friendly 2008, p. 32.
- Friendly 2008, p. 37.
- Tufte 2001, p. 53.
- (en) Hadley Wickham, ggplot2 : Elegant Graphics for Data Analysis, Springer Verlag, coll. « Use R », (DOI 10.1007/978-0-387-98141-3)
- Yau 2013, p. 93.
- Yau 2013, p. 96.
- Yau 2013, p. 104.
- Yau 2013, p. 109.
- Yau 2011, p. 94.
- « Le graphique en anneaux », sur ebsi.umontreal.ca (consulté le ).
- Yau 2011, p. 137.
- Yau 2011, p. 142.
- Bruno Déchamps, « Groupes socioprofessionnels (GSP) - Répartition », sur statapprendre.education.fr/ (consulté le ).
- Tufte 2001, p. 44.
- Yau 2011, p. 112.
- Yau 2011, p. 180-181.
- Yau 2011, p. 118.
- Yau 2011, p. 192-193.
- Toussaint Loua, Atlas statistique de la population de Paris. Paris: J. Dejey. 1873
- Yau 2011, p. 229.
- « Comment utiliser les Sparklines », sur Management et Performance, piloter.org, (consulté le )
- Yau 2011, p. 93.
- Tufte 2001, p. 16-20.
- Tufte 2001, p. 20-24.
- Yau 2011, p. 188-189.
- (en) Isabel Meirelles, Design for Information, Rockport Publishers, , p. 18
- Yau 2011, p. 157.
- Meirelles 2013, p. 31.
- Meirelles 2013, p. 39.
- « Newmap », sur newsmap.jp (consulté le )
- (en) Matthew Bloch, Shan Carter et Amanda Cox, « All of Inflation’s Little Parts », The New York Times, (lire en ligne)
- Meirelles 2013, p. 44.
- « 4 raisons qui expliquent comment les médias sociaux nous manipulent », sur Conseils en marketing, (consulté le )
- Martin Grandjean, « La connaissance est un réseau », Les Cahiers du Numérique, vol. 10, no 3, , p. 37-54 (lire en ligne, consulté le )
- (en) « Exhibition – David Bihanic », sur davidbihanic.com (consulté le ).
- (en) « Data Visualization and the Modern Imagination », sur Spotlight at Stanford (consulté le ).
Voir aussi
Articles connexes
- Représentation graphique d'une fonction mathématique
- Graphe

- Système d'information géographique
- Représentation par le graphisme et l'image
- Cartographie
- Cartographie d'information
- Flèche du temps
- Journalisme de données
- Datactivisme
- Visualisation d'informations
- Infographie
- Sémiologie graphique
- Science des données
- Tableau (statistique)
- Figures de Chernoff
- Représentation graphique
- Visualisation scientifique
- Journalisme de données
- Cynthia Brewer et ColorBrewer
Liens externes
- Ressource relative à la santé :
- (en) Michael Friendly (en) et Daniel Denis, « Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization », sur DataVis.ca
.svg.png.webp)
![[x_{1},x]](https://img.franco.wiki/i/dc134a8877859c2d88bfbfa68e4a0b1362aaa779.svg)