Unité structurale de la Terre
Les unités structurales de la Terre sont les couches de matières qui la composent.
Les principales unités structurales de la Terre sont la croûte, le manteau et le noyau. Chaque couche a ses caractéristiques particulières.
Hypothèses simplificatrices
Hypothèse de sphéricité
Le but essentiel de la géophysique interne est de dégager l'existence et d'étudier les propriétés des divers milieux qui composent l'intérieur de la Terre, et de décrire les méthodes mises en œuvre pour arriver à une connaissance assez précise de la distribution, en fonction de la profondeur, de la densité (c'est-à-dire de la masse volumique) des roches qui constituent le matériau terrestre. Il est clair que cette densité fournit des indications, malheureusement ambiguës, sur la composition chimique et minéralogique des roches en question. Nous avons en vue ici un modèle moyen de la Terre, et nous ferons donc différentes hypothèses simplificatrices en indiquant, le cas échéant, dans quelles circonstances l'une ou l'autre de ces hypothèses cesse d'être valable.
Nous supposons ainsi que la mécanique des milieux continus peut s'appliquer à travers l'approximation des milieux continus. Cette hypothèse implique que les propriétés du matériau se décrivent au moyen de fonctions continues, ou du moins continues par morceaux. En particulier, isolons par la pensée un élément de matière, de volume δV suffisamment petit pour être considéré mathématiquement comme élément différentiel, mais assez grand pour contenir de nombreux atomes ou molécules, et ainsi obéir aux lois de la physique macroscopique. La masse de cet élément de matière est δm et le centre de l'élément se trouve au point P. En vertu de l'hypothèse de continuité, on peut alors définir la densité au point P par
Cette fonction sera elle-même continue par morceaux à l'intérieur de la Terre.
Nous admettons que les propriétés physiques ne dépendent que de la profondeur z, et non des coordonnées géographiques. En d'autres termes, nous cherchons à construire un modèle de Terre possédant une symétrie sphérique. Cette hypothèse implique en particulier que toutes les surfaces d'égale densité (isopycniques), d'égale pression (isobares) et d'égale température (isothermes) sont confondues avec les surfaces d'égale pesanteur (équipotentielles), c'est-à-dire avec les surfaces de niveau.
Les images renvoyées par les sondes spatiales montrent en effet que la Terre, vue d'une distance suffisante, est une boule sphérique presque parfaite. Réduite à l'échelle d'un globe de 30 centimètres de diamètre, la rugosité de la surface topographique et l'asphéricité produite par la rotation, donnent lieu à des écarts par rapport à la forme sphérique parfaite inférieurs à 0,4 millimètre. Ainsi, un modèle sphérique constitue sans nul doute une bonne première approximation, qui pourra éventuellement servir de base pour construire des modèles tridimensionnels plus réalistes.
Cependant, le fait que la Terre tourne sur elle-même engendre un potentiel axifuge[1] qui a pour effet de produire un renflement à l'équateur et un aplatissement aux pôles. La figure d'équilibre ainsi produite dépend faiblement de la constitution interne du globe, mais ne s'écarte que très peu d'un ellipsoïde de révolution autour de l'axe polaire. En désignant par a le demi-grand axe, par c le demi-petit axe de cet ellipsoïde, et par R le rayon équivolumétrique (a2c)1/3, nous avons en chiffres ronds : a ≅ 6 378 km, c ≅ 6 356 km et R ≅ 6 371 km. On en déduit un aplatissement géométrique
de l'ordre de 1/300. La valeur précise de cet aplatissement fournit des renseignements sur la constitution interne de la Terre. La forme des surfaces de niveau théoriques, résultant de l'action simultanée de l'attraction gravifique et de la force axifuge, peut être déduite de la théorie des figures d'équilibre due à Clairaut, Laplace et Lyapounoff.
Hypothèse d'équilibre hydrostatique
Une autre hypothèse, rejoignant dans une certaine mesure celle de symétrie sphérique, stipule que l'état de tension qui règne à l'intérieur de la Terre est très voisin de celui qui y règnerait si toutes les roches étaient fondues. En d'autres termes, pour construire un profil de densité, on suppose que les contraintes se réduisent à une simple pression, par nature isotrope, dont la valeur s'obtient au moyen de l'équation d'équilibre hydrostatique
,
où P est cette pression, z la profondeur, ρ la densité, et g l'accélération gravifique. Connaissant la densité au centre, c'est-à-dire en z=R,
et à la surface, c'est-à-dire en z = 0, l'accélération gravifique à une profondeur quelconque est fournie par l'expression :
,
où G = 6,674 2 × 10−11 m3 s−2 kg−1 est la constante de gravitation de Newton. L'établissement de l'équation d'équilibre hydrostatique est très simple. Pour ce faire, considérons un cylindre vertical de section droite S s'étendant de la surface extérieure z=0 jusqu'au centre z=R. À l'intérieur de cette colonne de matériau, considérons un petit volume dont le centre est situé en P à la profondeur z, dont la face supérieure se trouve en z–½∆z et la face inférieure en z+½∆z. Pour que ce petit volume de matière ne se mette pas en mouvement, c'est-à-dire pour qu'il y ait équilibre statique, son poids ρg S ∆z doit être contrebalancé par la force due à la différence des pressions ∆P agissant sur les faces supérieure et inférieure, soit S ∆P. L'équation annoncée plus haut, à savoir dP = ρg dz, en découle en faisant tendre les surfaces supérieure et inférieure l'une vers l'autre à la profondeur z.
L'hypothèse de l'équilibre hydrostatique se justifie en rappelant que lorsqu'on soumet un solide à des forces extérieures engendrant des contraintes de cisaillement dont les valeurs dépassent les forces de cohésion internes du matériau, ce dernier cesse de résister à tout effort qui tend à le faire changer de forme, et selon sa nature et l'environnement dans lequel il est plongé, il se casse ou subit un phénomène de fluage. Ce seuil de résistance est, pour les roches non fissurées courantes, de l'ordre d'un kilobar (1 kb = 108 Pa). On se fait une idée plus précise de ce que cette contrainte représente en notant qu'elle correspond à un poids de dix kilogrammes-force distribué sur une section plane d'un millimètre carré. Il s'ensuit que les différences |σ2 – σ1|, |σ3 – σ2|, |σ1 – σ3| des tensions principales caractérisant l'état de tension du matériau en un point, ne peuvent pas dépasser des valeurs de l'ordre d'un kilobar.
D'autre part, la contrainte moyenne σ = ⅓ (σ1 + σ2 + σ3) représente, au signe près[2], la pression moyenne ou octaédrale 〈P〉 = –σ dont la valeur n'est pas limitée par le seuil de résistance de la roche à la profondeur z, mais croît en valeur absolue avec le poids de la colonne des roches situées au-dessus de cette profondeur. L'état hydrostatique étant caractérisé par les relations σ1 = σ2 = σ3, la pression octaédrale se confond pour un tel état avec la pression hydrostatique P, encore appelée pression lithostatique s'il s'agit de roches. Par conséquent, l'hypothèse d'un équilibre hydrostatique correspondra d'autant mieux à la réalité que σ sera grand par rapport à la plus grande des valeurs
, pour
Il est clair que nous pouvons utiliser l'équation d'équilibre hydrostatique pour estimer l'ordre de grandeur de σ à différentes profondeurs et utiliser, pour ce faire, des valeurs constantes pour la densité et la gravité, pourvu que ces dernières représentent des estimations réalistes pour la Terre. En prenant ainsi ρ = 3 300 kg/m3 et g = 10 m/s2, on trouve P = 10 kb à z = 30 km, P = 100 kb à z = 300 km, et P = 1 Mb à z = 3 000 km. Ces valeurs montrent que les conditions réelles à l'intérieur de la Terre (sauf dans les couches les plus externes) ne peuvent pas s'écarter très fort de l'équilibre hydrostatique. La détermination du champ de pesanteur de la Terre au moyen de l'observation des orbites de satellites artificiels a effectivement montré que sans être une figure d'équilibre parfaite, la forme de la Terre ne s'écarte que légèrement d'une telle figure[3].
Hypothèse d'homogénéité locale et d'isotropie
Une autre simplification des modèles résulte du fait que les outils employés pour arriver à une connaissance quantitative des propriétés physiques de la Terre possèdent nécessairement un pouvoir de résolution limité tant dans l'espace que dans le temps. En effet, toute mesure constitue une moyenne de la propriété étudiée dans un certain volume pendant un certain intervalle de temps. Or, la plupart de nos connaissances quantitatives sur la structure interne de la Terre sont basées sur des méthodes sismiques utilisant comme moyen d'investigation des ondes élastiques dont les longueurs d'onde Λ sont comprises en gros entre un kilomètre et plusieurs milliers de kilomètres. La résolution spatiale obtenue dans la détermination géophysique des propriétés des roches profondes est donc de l'ordre de Λ3, c'est-à-dire au mieux 1 km3. Par contre, les roches auxquelles on a directement accès, essentiellement les roches de surface, peuvent être étudiées par des méthodes de laboratoire qui permettent d'en acquérir une connaissance à l'échelle de 1 µm3 au moyen du microscope ou de la microsonde, et même à l'échelle de 10−12 µm3 au moyen du diffractomètre à rayons X. Il est important de garder à l'esprit la différence entre les échelles considérées par le géophysicien d'une part, le pétrographe et le minéralogiste d'autre part, si l'on ne veut pas commettre parfois de grossières erreurs dans l'interprétation pétrologique des données fournies par la géophysique interne.
Le fait de considérer des moyennes sur des volumes de roches ayant des dimensions généralement bien supérieures à un kilomètre cube nous permet, la plupart du temps, de faire deux hypothèses simplificatrices supplémentaires sans lesquelles nous ne serions sans doute pas arrivés aux connaissances que nous possédons actuellement sur la structure interne de la Terre. Il s'agit des hypothèses d'élasticité isotrope et d'homogénéité locale, essentielles dans la formulation de la sismologie classique.
Les roches solides, qui constituent la majorité du matériau terrestre, sont constituées d'assemblages de grains de minéraux divers ayant des dimensions linéaires en général micrométriques à millimétriques, mais pouvant parfois atteindre le centimètre et davantage. Ces grains tiennent ensemble grâce à des ciments formés de grains beaucoup plus petits dont la nature chimique est souvent la même que celle des grains dont ils assurent la cohérence. Les minéraux eux-mêmes sont faits d'assemblages de cristaux, de microcristaux ou de verres. Un cristal est caractérisé par des propriétés de symétrie bien spécifiques qui font que certains de ses attributs physiques dépendent de la manière dont il est orienté. Ainsi faut-il déterminer en tout 21 paramètres distincts pour arriver à décrire correctement les propriétés élastiques d'un cristal du système triclinique, et pouvoir étudier la propagation des ondes élastiques (phonons) dans un cristal pareil. Lorsqu'on augmente le nombre d'éléments de symétrie, le nombre de paramètres élastiques indépendants diminue. Ainsi, pour le système monoclinique, ce nombre n'est plus que de 13, pour passer à 9 dans le système orthorhombique, à 7 ou 6, selon la classe cristalline envisagée, dans les systèmes quadratique (tétragonal) et trigonal, à 5 dans le système hexagonal, et à 3 dans le système cubique.
Un matériau parfaitement isotrope, comme c'est le cas de la plupart des verres, est caractérisé par seulement deux paramètres élastiques distincts. À l'intérieur de la Terre, les cristaux dans les assemblages minéraux et rocheux ne sont généralement pas orientés selon une direction préférentielle, mais plutôt de manière aléatoire. Il en résulte que l'effet élastique global du volume de roches échantillonné par le passage d'ondes sismiques est isotrope en très bonne approximation, sauf cas d'espèce. Ces cas d'espèce se rencontrent notamment dans des régions du globe où un métamorphisme important a donné lieu à une schistosité des roches à grande échelle, et dans des régions où des courants de matière ont pu orienter ou réorienter une partie des axes cristallins dans une direction privilégiée. On pense aussi actuellement que le matériau (essentiellement du fer) composant le noyau interne de la Terre, à savoir la région qui s'étend du centre à environ 1 220 km de rayon, est légèrement anisotrope. Le comportement élastique anisotrope dans ces régions fait le sujet de nombreuses études sismologiques spécialisées, et fournit des indications très importantes concernant divers processus tectoniques ou autres qui s'y passent ou s'y sont passés. Néanmoins, à l'échelle du globe tout entier, il s'agit d'un effet plutôt marginal qu'il convient de négliger en première approximation dans la construction d'un modèle sphérique pouvant servir de référence. En effet, l'anisotropie à l'intérieur de la Terre se chiffre tout au plus à quelques pourcents par rapport à une valeur de référence obtenue en supposant le matériau isotrope (alors que l'anisotropie dans les monocristaux peut se chiffrer en dizaines de pourcents et davantage).
D'autre part, s'il est relativement facile de montrer, par des études sismologiques appropriées, que les vitesses des ondes sismiques varient avec la direction de propagation et que, par conséquent, le matériau est anisotrope, il est presqu'impossible en pratique de déterminer la valeur des paramètres élastiques, voire seulement le nombre exact des paramètres en cause. Pour faire la théorie de la propagation des ondes sismiques dans un milieu anisotrope, on suppose d'habitude qu'il s'agit d'aléotropie (= isotropie transverse). Il existe alors un plan dans lequel toutes les directions sont équivalentes — le plus souvent le plan horizontal par suite de la stratification naturelle — les propriétés n'étant pas les mêmes dans la direction de l'axe vertical. On montre que ce dernier type de symétrie revient en fait à celui du système cristallin hexagonal, et que par conséquent il existe cinq paramètres élastiques distincts pour l'isotropie transverse. Si la notion d'isotropie concerne l'invariance d'une propriété lors d'une rotation quelconque, une autre notion fondamentale, celle d'homogénéité, concerne l'invariance d'une propriété lors d'une translation quelconque. Nous avons vu qu'une roche typique, considérée à une échelle suffisamment petite, se présente le plus souvent comme un assemblage inhomogène. Cependant, en raison du pouvoir de résolution limité des ondes sismiques, on ne peut mesurer que des valeurs moyennes qui font apparaître le milieu comme plus homogène qu'il n'est en réalité. En fait, la pression résultant du propre poids du matériau terrestre comprime celui-ci au fur et à mesure que la profondeur augmente. Il s'ensuit que même si la Terre était composée d'un matériau homogène d'un point de vue chimique et minéralogique, ce qui est loin d'être le cas, les propriétés physiques ne pourraient pas être uniformes. Toutefois, on admet que les hauteurs d'échelle pour les variations des propriétés moyennes sont grandes par rapport aux longueurs d'onde des ondes sismiques ordinaires. On a pu vérifier a posteriori cette hypothèse essentielle de la sismologie classique. Sauf cas de transitions brusques, on admet donc qu'il y a homogénéité locale.
Paramètres élastiques et vitesses des ondes de volume
Module de Young et coefficient de Poisson
D'un point de vue mécanique, la description complète d'un modèle sphérique élastiquement isotrope et localement homogène se fait au moyen de trois variables qui sont des fonctions de la profondeur, à savoir la densité ρ et deux paramètres élastiques distincts. Au lieu de la profondeur z, on considère souvent la distance au centre r = R – z. Au lieu de paramètres élastiques, on peut aussi utiliser les vitesses de propagation des ondes volumiques en fonction de la profondeur. Les ingénieurs et les physiciens utilisent, le plus souvent, le module d'élasticité de Young E et le coefficient de Poisson ν comme paramètres élastiques indépendants. Lorsqu'on applique à un fil cylindrique de diamètre ϕ, de section droite S = ¼ π ϕ2 et de longueur ℓ une force F, le fil s'allongera pour atteindre une longueur ℓ′ tout en réduisant son diamètre à ϕ′. On trouve expérimentalement que lorsque la force ne dépasse pas un certain seuil, appelé la limite d'élasticité, l'allongement relatif (ℓ′ – ℓ)/ℓ est proportionnel à F et inversement proportionnel à S, la constante de proportionnalité étant 1/E. D'autre part, le coefficient de Poisson est fourni par le rapport de la variation relative du diamètre (ϕ′ – ϕ)/ϕ à l'allongement relatif (ℓ′ – ℓ)/ℓ, c'est-à-dire :
.
Module de compression
En géophysique interne, on emploie plutôt deux autres paramètres élastiques, le coefficient d'incompressibilité κ et le coefficient de cisaillement μ.
Le coefficient d'incompressibilité, encore appelé module de compression (en anglais : bulk modulus), se définit comme suit : Considérons un volume de matière V et comprimons-le jusqu'au volume V+∆V à l'aide d'un incrément de pression ∆P. Le coefficient d'incompressibilité est alors fourni par le rapport négatif de la variation de pression à la variation relative du volume, soit
et représente donc une mesure de la résistance opposée par le matériau à un changement de volume. Le signe négatif est mis conventionnellement parce que les matériaux se contractent sous l'effet d'une augmentation de pression et se dilatent sous l'effet d'une diminution de pression. La quantité κ est donc essentiellement positive. L'expérience précédente peut s'effectuer sous diverses conditions thermodynamiques, qu'il convient de spécifier. Ainsi, on peut plonger l'échantillon dans un thermostat et le comprimer de manière suffisamment lente pour que sa température ne varie pas. Il s'agit alors d'une transformation isotherme, ce qu'on indique en ajoutant un indice approprié au symbole κ. Ce dernier se notera alors κT. On peut aussi procéder à une compression suffisamment rapide pour que l'échantillon n'échange qu'une quantité négligeable de chaleur avec le milieu environnant, auquel cas il s'agit d'une expérience isentropique (adiabatique si la transformation est en plus réversible). Ce dernier cas est réalisé en bonne approximation lorsque des ondes élastiques produites lors d'un séisme compriment ou dilatent les roches sur leur passage. Le module de compression correspondant est noté κS. Remarquons que le volume initial V de l'échantillon considéré peut être le volume spécifique ρ−1 et que pour cerner des propriétés suffisamment ponctuelles du matériau, au sens de la mécanique des milieux continus, il y a lieu de considérer des éléments différentiels suffisamment petits, de sorte que le module de compression en un point est en général défini, pour des conditions adiabatiques, par :
Le module de compression, tout comme le module de Young, possède les dimensions d'une force par unité de surface et s'exprime donc en unités M L−1 T−2. Les valeurs pour les roches terrestres en sont de l'ordre de 1011 Pa, ou encore 1 Mb.
Module de rigidité
D'autre part, le coefficient de cisaillement, qu'on appelle aussi module de rigidité ou module de torsion (en anglais : shear modulus), se définit à partir d'expériences qui mettent en cause non pas un changement de volume, mais un changement de forme correspondant à un cisaillement, une torsion, une rotation différentielle, etc. Sur base de considérations thermodynamiques générales, on peut montrer qu'il n'y a pas lieu de distinguer entre le coefficient de cisaillement adiabatique μS et le coefficient de cisaillement isotherme μT, autrement dit μ = μS = μT. En outre, il est un fait d'expérience de tous les jours que les liquides et les gaz n'opposent pas de résistance appréciable lorsqu'on essaie de leur imprimer une forme quelconque, par exemple en versant de l'eau dans un vase. Nous caractériserons donc l'état fluide par le fait que μ = 0. Pour les corps simples tels que le fer, le cuivre, l'étain, le plomb, etc., il existe une loi empirique établie par Sutherland vers la fin du XIXe siècle, qui stipule que lorsqu'on approche le point de fusion d'un tel matériau, le module de rigidité tend vers zéro selon une loi quadratique, soit
,
où Tf est la température absolue de fusion et μ0 la rigidité du matériau au zéro absolu.
Vitesses des ondes de volume
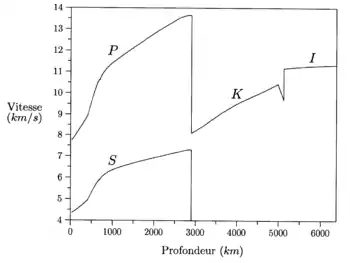
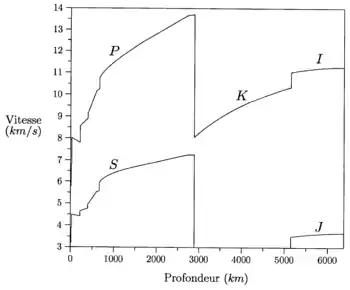
En réalité, les valeurs numériques des coefficients élastiques à l'intérieur de la Terre, de même d'ailleurs que celles de la densité, ne sont connues que par des considérations indirectes. Par contre, il est possible de déterminer par des méthodes relativement simples les vitesses de propagation des ondes élastiques émises aux foyers des tremblements de terre et se transmettant de proche en proche à travers l'intérieur de la Terre. En acceptant la validité des hypothèses simplificatrices énoncées plus haut, il est possible de montrer qu'il existe deux types d' ondes de volume : des ondes longitudinales, pour lesquelles les particules matérielles mises en mouvement par ces ondes vibrent autour de leur position d'équilibre dans la direction de propagation de l'onde elle-même, et des ondes transversales, pour lesquelles le mouvement des particules matérielles s'effectue perpendiculairement à la direction de propagation.
Les ondes longitudinales sont caractérisées par une vitesse de phase
,
où il est sous-entendu que κ désigne le module de compression adiabatique noté κS plus haut. D'autre part, la vitesse de phase des ondes transversales est donnée par :
.
Or, il est un fait d'expérience que la plupart des corps diminuent de volume lorsqu'on les soumet à des forces compressives, de sorte que κ > 0. De même, nous constatons qu'en général μ ≥ 0. Dès lors, on a α > β. Il s'ensuit que les ondes longitudinales se transmettent plus vite à travers la Terre que les ondes transversales. Les deux sortes d'ondes sont émises en même temps au foyer, mais les ondes longitudinales prennent de plus en plus d'avance sur les ondes transversales au fur et à mesure que la distance au foyer augmente. Après un tremblement de terre, les ondes longitudinales sont donc les premières à être enregistrées, et c'est pourquoi les sismologues les appellent ondes P, abréviation de Primae undae (Premières ondes). Les ondes transversales sont enregistrées en second lieu et sont désignées pour cette raison par ondes S, abréviation de Secundae undae (Secondes ondes). Dans un matériau gazeux ou liquide qui n'oppose aucune résistance à des forces de cisaillement, il n'existe pas d'ondes S (puisque le coefficient de rigidité y est nul), et les ondes P correspondent à des ondes sonores liées à des variations de pression dont la vitesse de propagation est :
Le travail essentiel de la sismologie classique consistait, jusque vers le milieu des années 1960, à déterminer avec le plus de détails possibles les distributions de α et β en fonction de la profondeur, à partir de vitesses apparentes de propagation en surface. La solution classique était celle obtenue par Harold Jeffreys et Keith Bullen, datant pour l'essentiel des années 1930. Une solution plus récente est celle retenue par Adam Dziewonski et Don Anderson pour le modèle terrestre PREM (Preliminary Reference Earth Model), qui date de 1981.
Paramètre sismologique
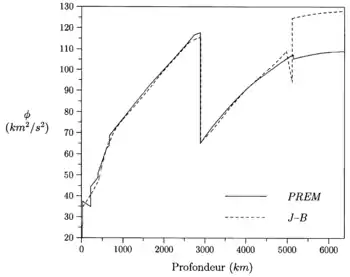
À partir des courbes de vitesses des ondes P et S on obtient le paramètre sismologique Φ, rapport du module de compression à la densité, c'est-à-dire :
Ce dernier joue un rôle essentiel dans la détermination de la distribution de la densité à l'intérieur de la Terre. En fait, dans la plus grande partie de la Terre, les valeurs récentes de Φ ne sont pas considérablement changées par rapport aux valeurs anciennes utilisées par Harold Jeffreys et Keith Bullen. Bien sûr, dans le détail, il y a eu des progrès significatifs. Ainsi, on a pu mettre en évidence une structure assez complexe des couches s'étendant de la surface extérieure jusqu'à environ 700 kilomètres de profondeur, région qu'on appelle communément le manteau supérieur. En outre, on a pu établir que les couches les plus centrales, s'étendant du centre jusqu'à un rayon d'environ 1220 kilomètres, que l'on appelle le noyau interne ou encore la graine, transmettent les ondes transversales et se comportent donc comme un matériau solide, alors que les travaux classiques de Jeffreys et Bullen supposaient que la graine était liquide et ne transmettait pas les ondes transversales, à l'instar du noyau externe situé entre 2 900 et 5 200 kilomètres de profondeur.
Principales subdivisions de l'intérieur de la Terre

Croûte terrestre et discontinuité de Mohorovičić
On vient de citer, sur base de la distribution des vitesses des ondes P et S, quelques unités structurales remarquables à l'intérieur de la Terre, telles la graine et le manteau supérieur. Afin de se familiariser avec la terminologie utilisée en géophysique interne pour pouvoir comprendre des articles plus techniques, il convient d'introduire l'ensemble de ces unités et d'en préciser les caractéristiques essentielles, mais sans aborder ici les méthodes par lesquelles on a pu les mettre en évidence. En s'enfonçant vers l'intérieur, à partir de la surface solide extérieure de la Terre, on rencontre trois régions principales qui sont la croûte, le manteau et le noyau.
La croûte terrestre, appelée « écorce terrestre » avant le début du XXe, constitue la région la plus externe. Elle est limitée à sa base par une surface de discontinuité de première espèce[4] d'extension quasi-globale, la « surface de Mohorovičić ». L'épaisseur de la croûte, autrement dit la profondeur à laquelle se trouve la surface de Mohorovičić, est variable d'un endroit à l'autre et implique donc que la croûte constitue une grande unité géophysique pour laquelle l'idée d'une symétrie sphérique est dénuée de sens. En moyenne, sous le fond des océans, l'épaisseur de la croûte avoisine 6 à 7 kilomètres, ce qui place la surface de Mohorovičić en moyenne entre 10 et 12 kilomètres de profondeur à partir de la surface libre, définie comme la frontière entre le globe terrestre proprement dit et l'atmosphère. Par contre, sous les continents, la surface de Mohorovičić s'enfouit bien plus profondément dans la Terre, puisqu'on la rencontre en moyenne vers 35 kilomètres de profondeur.
Dans certaines régions continentales, en bordure d'un océan, la croûte s'amincit jusqu'à 20 kilomètres. Par contre, dans plusieurs régions montagneuses, elle s'épaissit jusqu'à plus de 60 kilomètres. La croûte continentale se distingue de la croûte océanique, non seulement par sa plus grande épaisseur, mais aussi par sa composition chimique et minéralogique. Pour l'essentiel, la croûte océanique est constituée de basaltes assez denses comparés aux matériaux formant la croûte continentale. Cette dernière est traditionnellement subdivisée en (1) croûte supérieure, composée de roches parmi lesquelles le granite semble prédominer et à laquelle on associe souvent une densité moyenne d'environ 2,7 g/cm3, et en (2) croûte inférieure, composée de basaltes dont la composition moyenne ne coïncide pas avec les basaltes océaniques. On leur attribue souvent une densité moyenne d'environ 2,9 g/cm3.
La croûte continentale forme un ensemble fort hétérogène, expression des très nombreux phénomènes géologiques et géodynamiques qui l'ont façonnée et qui continuent à la façonner. On ne peut donc pas fixer avec précision la frontière entre croûte continentale supérieure (upper continental crust) et croûte continentale inférieure (lower continental crust). Là où la frontière est suffisamment marquée pour être mise en évidence par des méthodes sismiques, on parle de « surface de Conrad ». D'autre part, au sommet de la croûte aussi bien continentale qu'océanique, on trouve en de nombreux endroits des couches de sédiments et de roches sédimentaires dont la densité est généralement comprise entre 1,5 et 2,5 g/cm3, et dont l'épaisseur cumulée est éminemment variable, allant de l'absence complète de sédiments à plusieurs kilomètres de roches sédimentaires. La croûte terrestre et l'ensemble de l'hydrosphère (océans, mers, lacs, cours d'eau, réserves d'eau souterraine) ne représentent qu'environ 0,8 % du volume total et seulement légèrement plus de 0,4 % de la masse totale de la Terre. À l'échelle du globe tout entier, on ne tient donc généralement pas compte de l'épaisseur variable et de la grande complexité structurale de la croûte, et on la remplace par une ou plusieurs couches sphériques reflétant seulement grossièrement ses propriétés moyennes. Cependant, il faut remarquer que c'est des couches supérieures de la croûte que nous sommes tributaires pour notre approvisionnement en minerais utiles et en hydrocarbures. Avant l'avènement de la théorie des plaques lithosphériques, vers le milieu des années 1960, c'était surtout l'étude de la croûte qui constituait l'essentiel des activités scientifiques des géologues. D'autre part, des méthodes géophysiques particulières sont utilisées pour l'exploration de la croûte.
Manteau terrestre et CMB
Directement sous la surface de discontinuité de Mohorovičić commence le manteau terrestre, qui s'étend jusqu'à une profondeur moyenne légèrement inférieure à 2 900 km. Le manteau, à lui seul, représente environ 82,7 % du volume total et environ 67 % de la masse totale de la Terre. On le subdivise traditionnellement en manteau supérieur et manteau inférieur. Actuellement, dans le modèle PREM, on considère que le manteau supérieur (upper mantle) se compose d'une région comprise entre les profondeurs de 24,4 et 80 km, désignée par LID (layer at intermediate depth, couche à profondeur intermédiaire), d'une région s'étendant de 80 à 220 km de profondeur et caractérisée par une diminution des vitesses des ondes sismiques P et S avec la profondeur, d'où son appellation couche à moindre vitesse [expression plus correcte que l'expression anglaise low velocity zone (LVZ) ou low velocity layer (LVL)], et d'une région de transition (transition zone), subdivisée elle-même en trois couches distinctes : de 220 à 400 km, de 400 à 600 km, de 600 à 670 km, caractérisées par des gradients de vitesses plus importants que dans les autres régions. Le manteau inférieur (lower mantle) est lui-même subdivisé dans le modèle PREM en trois couches : de 670 à 771 km, de 771 à 2 441 km, de 2 441 à 2 891 km. La couche la plus basse (appelée « région D″ ») se caractérise par des gradients de vitesses très faibles.
Le manteau inférieur est séparé à sa base, à 2 891 km de profondeur, par une surface de discontinuité majeure de première espèce qui le sépare de la région située en dessous, à savoir le noyau terrestre. Cette surface est parfois appelée surface de Gutenberg (ou surface de Wiechert-Gutenberg), mais une appellation plus courante est CMB, abréviation de (en) core-mantle boundary. En franglais, on la nomme aussi interface noyau-manteau.
Noyau terrestre et ICB
Dans le modèle PREM, le noyau terrestre se subdivise en deux régions, le noyau externe (outer core), liquide car caractérisé par l'absence d'ondes S, s'étendant de 2891 à 5 149,5 km de profondeur, et le noyau interne ou graine (inner core), solide à l'instar du manteau et de la croûte, s'étendant de la surface de Lehmann ou encore ICB (pour inner core boundary ; en franglais, interface graine-noyau) à 5 149,5 km de profondeur jusqu'au centre à 6 371 km de profondeur. Au total, le noyau représente environ 16,5 % du volume et un peu moins du tiers de la masse de la Terre. Notons que le rayon de la graine, approximativement 1 221 km, vaut environ 70 % du rayon de la Lune (1 738 km).
Le noyau est la région dans laquelle la partie principale du champ géomagnétique est engendrée par un effet de dynamo autoexcitée et, pour cela, mérite une étude particulière (voir Dynamo terrestre). D'autre part, la formation du noyau pose un ensemble de questions géophysiques, géochimiques et cosmochimiques très intéressantes. On considère, en effet, que le noyau est pour l'essentiel composé de fer et de nickel, contrairement au manteau et à la croûte qui sont faits surtout de silicates nettement moins denses. La formation du noyau a dû libérer une formidable quantité d'énergie gravifique dont il convient de ne pas sous-estimer l'influence sur l'évolution géodynamique de la Terre. Le noyau terrestre renferme la réponse à de nombreuses questions que les géophysiciens se posent, et constitue actuellement un domaine d'investigation privilégié. En particulier, si le noyau dans son ensemble s'est probablement formé très vite après la formation de la Terre elle-même, il y a environ 4,5 milliards d'années, on pense que la graine est toujours en train de se former au détriment du noyau liquide et de pourvoir à l'énergie nécessaire pour maintenir en action la dynamo produisant le champ géomagnétique.
| Région | Sous-région | Épaisseur (km) |
Caractérisation |
|---|---|---|---|
| Océan mondial | 3,0 | 1 couche liquide | |
| Croûte | 21,4 | 2 couches solides | |
| croûte supérieure | 12,0 | type granitique | |
| croûte inférieure | 9,4 | type basaltique | |
| Manteau | 2 866,6 | 8 couches solides | |
| LID | 55,6 | solide aléotrope | |
| LVZ | 140,0 | solide anisotrope | |
| zone de transition | 450,0 | 3 couches isotropes | |
| manteau inférieur | 2 221,0 | 3 couches isotropes | |
| Noyau | 3 480,0 | 2 couches | |
| noyau externe | 2 258,5 | liquide | |
| graine | 1 221,5 | solide |

Le tableau ci-dessus fournit une brève caractérisation du modèle PREM basée sur des données fournies par la sismologie. Il faut remarquer que la nomenclature utilisée en géodynamique ne coïncide pas avec la nomenclature fournie ci-dessus. La figure ci-contre indique la correspondance entre les diverses régions sismologiques et géodynamiques. On remarquera que parmi les propriétés physiques ce ne sont pas les vitesses de propagation des ondes sismiques qui contrôlent les phénomènes géodynamiques, mais surtout la densité et la résistance mécanique des roches composant les diverses couches. Ainsi, en géodynamique, on divise la Terre en trois grandes structures : la lithosphère, l'asthénosphère et la mésosphère.
La lithosphère comprend la croûte et le LID et se subdivise en lithosphère continentale et lithosphère océanique selon qu'elle comprend une croûte de type continental ou de type océanique. Elle oppose dans l'ensemble une grande résistance aux déformations et se comporte, du point de vue mécanique, comme un matériau cassant. C'est dans la lithosphère que se produisent la grande majorité des tremblements de terre. On considère que la lithosphère est morcelée en un petit nombre de plaques (en anglais : lithospheric plates) dont les mouvements relatifs déterminent les processus tectoniques que nous observons à la surface de la Terre. Cette théorie des plaques lithosphériques, qui a vu le jour vers le milieu des années 1960, a permis d'unifier de très nombreux concepts géophysiques et géologiques. Elle a provoqué une véritable révolution dans les disciplines s'occupant de l'étude de la Terre, rendant désuets les traités de tectonique publiés avant 1965.
En dessous de la lithosphère, à une profondeur variable selon qu'il s'agit de lithosphère continentale (environ 120 km en moyenne) ou océanique (environ 60 km en moyenne), commence une région caractérisée par une diminution très accusée de la résistance mécanique, d'où son appellation d'asthénosphère (littéralement : sphère faible). Son épaisseur est, en moyenne, 160 km sous les océans et 100 km sous les continents. On la délimite sismiquement par les frontières de la zone à moindre vitesse. La raison physique de l'existence d'une asthénosphère tient au fait que dans cette zone les effets dus à l'augmentation de la température avec la profondeur l'emportent sur les effets d'augmentation de pression avec la profondeur, amenant la température réelle au voisinage de la température de fusion de certaines roches abondantes à ces profondeurs. Nous assistons donc dans cette zone à des fusions partielles qui ont pour résultat de diminuer de manière significative le module de cisaillement effectif, créant ainsi une relative faiblesse mécanique du matériau en même temps qu'une diminution appréciable de la vitesse des ondes S et P.
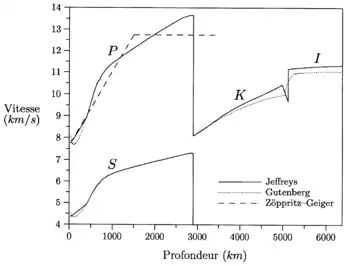
En dessous de l'asthénosphère, dans la mésosphère (c'est-à-dire sphère du milieu), les effets de pression l'emportent sur les effets de température et éloignent de nouveau la courbe de la température de fusion de la courbe de la température réelle, rendant le reste du manteau solide mais plus ductile que la lithosphère. La solution classique de Jeffreys et Bullen pour les vitesses des ondes de volume ne montrait pas de zone à moindre vitesse, mais qu'une telle zone fut retenue dans la solution proposée par Beno Gutenberg, dont l'aspect général restait toutefois très proche de la solution de Jeffreys et Bullen, sauf en ce qui concerne la présence d'une zone à moindre vitesse dans le manteau supérieur et l'interprétation fort différente d'une étroite zone de transition entre le noyau externe et le noyau interne. Pendant près d'un quart de siècle, la présence ou non de l'asthénosphère fut un sujet assez controversé, car la qualité des observations sismologiques ne permettait de trancher, à l'époque, ni dans un sens ni dans l'autre. Toutefois, l'observation d'une atténuation plus accusée des ondes de volume vers 100 km de profondeur plaidait en faveur de l'existence d'une zone de relative faiblesse, et donc de plus grande dissipation de l'énergie élastique. Ce ne sont pourtant pas les ondes de volume, mais les ondes de surface et les oscillations libres qui ont permis d'établir, vers 1960, la présence d'une asthénosphère de manière indiscutable.
Le tableau ci-dessous fournit quelques informations supplémentaires sur les principales régions de la Terre. On remarquera que les caractéristiques mentionnées ici ne coïncident pas toujours parfaitement avec celles du modèle PREM, et reflètent assez bien les incertitudes qui restent encore attachées à notre connaissance des propriétés moyennes de la Terre. L'ensemble manteau plus noyau représente à lui seul environ 99,6 % de la masse totale de la Terre. Il en résulte que malgré l'importance majeure que possède la croûte pour l'activité humaine, une théorie de l'intérieur de la Terre est nécessairement avant tout une théorie du manteau et du noyau. En outre, la croûte est le fruit d'une histoire compliquée qui semble être particulière à la Terre et ne pas s'être passée de la même manière sur d'autres planètes du système solaire. Pour cette raison, l'étude de la croûte n'intéresse la géophysique interne que dans la mesure où elle est susceptible de fournir des renseignements sur le manteau sous-jacent. Ce point de vue est à l'opposé de celui de la géologie, pour laquelle la croûte représente le principal sujet d'étude.
| Région | Rayon inférieur (km) |
Rayon supérieur (km) |
Densité (g/cm3) |
Masse (kg) |
Masse (%) |
|---|---|---|---|---|---|
| Atmosphère | 6 371 | — | — | 5,2 × 1018 | 10−6 |
| Hydrosphère | 6 369 ± 2 | 6 371 | 1,0 | 1,2 × 1021 | 0,0002 |
| Croûte | 6 350 ± 2 | 6 369 ± 2 | 2,8 ± 0,2 | 2,4 × 1022 | 0,004 |
| Manteau | 3 485 ± 13 | 6 350 ± 2 | 4,5 ± 0,1 | 4,1 × 1024 | 0,672 |
| Noyau | 1 217 ± 35 | 3 485 ± 13 | 10,9 ± 0,5 | 1,8 × 1024 | 0,306 |
| Graine | 0 | 1 217 ± 35 | 12,3 ± 1,2 | 1,1 × 1023 | 0,018 |
Notes et références
- Dans les ouvrages en français, il est de plus en plus courant de remplacer les vocables de force ou de potentiel centrifuge par les vocables plus corrects de force ou de potentiel axifuge.
- En physique et en géophysique, il est d'usage de compter positivement les contraintes normales qui tendent à étirer les corps, c'est-à-dire les tractions, et négativement celles qui tendent à les comprimer, c'est-à-dire les pressions. En mécanique des sols, on utilise en général une convention de signe contraire.
- L'hypothèse d'un équilibre hydrostatique global est nettement moins justifiée dans le cas de corps planétaires solides beaucoup plus petits que la Terre. Dans le cas de la Lune, par exemple, la pression centrale est seulement d'environ cinquante kilobars, pression atteinte dans la Terre vers cent kilomètres de profondeur.
- On appelle « surface de discontinuité de première espèce » relative à une propriété physique quelconque représentée par une fonction f(P), l'ensemble des points supposés former une surface dans l'espace physique à trois dimensions sur laquelle la fonction f(P) est discontinue. Par contre, sur une « surface de discontinuité de seconde espèce », la fonction f(P) elle-même reste continue, mais son gradient est discontinu.
Voir aussi
Articles connexes
Bibliographie
- M. Cara (1989). Géophysique, Dunod-Bordas « Géosciences », Paris. (ISBN 2-04-012340-7).
- J. Dubois & M. Diament (1997). Géophysique, Masson, Paris. (ISBN 2-225-83033-9).
- B.F. Howell (1969). Introduction à la géophysique, Masson, Paris. [Manuel de référence sur la géophysique interne avant l'avènement de la théorie des plaques tectoniques. Reste intéressant à condition de consulter aussi des textes récents, par exemple le livre en anglais de C.M.R. Fowler (voir ci-dessous).]
- P. Mechler (1982). Les méthodes de la géophysique, Dunod-Bordas « Dunod Université », Paris. (ISBN 2-04-010414-3).
- Jean Paul Poirier, Les Profondeurs de la terre, Masson, coll. « Cahiers des sciences de l'univers », , 2e éd., 140 p. (ISBN 978-2-225-85223-7)
En langue anglaise
- D.L. Anderson (1989). Theory of the Earth, Blackwell Scientific Publications, Oxford. (ISBN 0-86542-123-4). Theory of the Earth
- K.E. Bullen (1975). The Earth's Density, Chapman & Hall, London. (ISBN 0-412-10860-7).
- C.M.R. Fowler (1990). The Solid Earth (An Introduction to Global Geophysics), Cambridge University Press, Cambridge. (ISBN 0-521-38590-3).
- B. Gutenberg, editor (1951). Internal Constitution of the Earth, Dover Publications, New York. [Ce volume, bien que très ancien, contient encore beaucoup d'informations valables et permet de se faire une idée de la façon de dégager lentement les grandes unités structurales de la Terre, dans la première moitié du XXe siècle.]
- H. Jeffreys (1970). The Earth — Its Origin, History and Physical Constitution (Fifth Edition), Cambridge University Press, Cambridge. (ISBN 0-521-07278-6). [Avant-dernière édition de la bible de haut niveau écrite pour les géophysiciens internes par l'un des géophysiciens les plus connus du XXe siècle, même s'il ne s'est jamais rallié à la théorie des plaques lithosphériques).]
- P.J. Smith (1973). Topics in Geophysics, The Open University Press, Milton Keynes, U.K. (ISBN 0-335-02350-9).