Treillis (ensemble ordonné)
En mathématiques, un treillis[1] (en anglais : lattice) est une des structures algébriques utilisées en algèbre générale. C'est un ensemble partiellement ordonné dans lequel chaque paire d'éléments admet une borne supérieure et une borne inférieure. Un treillis peut être vu comme le treillis de Galois d'une relation binaire.
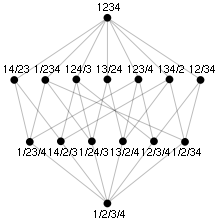
Il existe en réalité deux définitions équivalentes du treillis, une concernant la relation d'ordre citée précédemment, l'autre algébrique.
Exemples et contre-exemples préliminaires
Tout ensemble muni d'une relation d'ordre total est un treillis. Par exemple, tout ensemble de réels muni de l'ordre usuel.
Parmi les ensembles munis d'une relation d'ordre partiel, des exemples simples de treillis sont issus des relations d'ordre « est inclus dans » et « divise ».
- L'ensemble des parties d'un ensemble muni de l'inclusion forme un treillis où la borne supérieure est l'union et la borne inférieure l'intersection.
- Si une partie d'un treillis est stable par borne supérieure et borne inférieure, elle forme un treillis (pour l'ordre restreint). C'est ainsi que l'ensemble des ouverts d'un espace topologique (toujours muni de l'inclusion) et un filtre sur un ensemble forment des treillis.
- Cette condition de stabilité n'est pas nécessaire :
- l'ensemble des intervalles fermés de ℝ (y compris l'ensemble vide) est un treillis dont la borne inférieure est l'intersection et dont la borne supérieure n'est pas toujours l'union : ainsi la borne supérieure des intervalles [1, 3] et [4, 5] est l'intervalle [1, 5] ;
- l'ensemble des relations d'équivalence sur un ensemble donné est un treillis (ordonné par la finesse entre relations binaires) dont la borne inférieure est l'intersection (sur les graphes) mais la borne supérieure est la relation d'équivalence engendrée par l'union.
- L'ensemble des entiers naturels muni de la relation « divise » forme un treillis, où la borne supérieure est le PPCM et la borne inférieure est le PGCD.
- Pour tout entier n ≥ 3, l'ensemble des entiers de 1 à n, muni de la relation d'ordre « divise », n'est pas un treillis car la paire {n, n – 1} n'a pas de borne supérieure ni même de majorant (car tout multiple de n et n – 1 est multiple de n(n – 1), qui est > n).
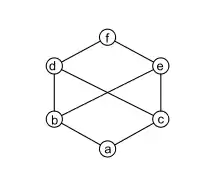
- Il ne suffit pas que chaque paire possède des majorants et des minorants pour obtenir un treillis. Ainsi, dans la relation décrite par le diagramme de Hasse ci-contre, la paire {b, c} admet trois majorants d, e et f, mais pas de borne supérieure car {d, e, f} ne possède pas de plus petit élément.
Définition algébrique
Un treillis est un ensemble E muni de deux lois internes habituellement notées ⋁ et ⋀ vérifiant :
- les deux lois sont commutatives et associatives ;
- pour tous a et b de E : (loi d'absorption).
La loi d'absorption entraîne l'idempotence de tout élément a de E pour les deux lois[2] :
- .
À partir d'une telle structure on peut définir sur E une relation d'ordre, ici notée ≤, de la manière suivante :
- .
On peut montrer que cette relation est bien une relation d'ordre (éventuellement partielle). La propriété d'associativité assure la transitivité. La propriété d'idempotence assure la réflexivité. La commutativité assure l'antisymétrie. Grâce aux deux propriétés d'absorption, on peut aussi montrer que
- .
On peut alors vérifier que
- ,
ce qui assure que est bien un treillis au sens des ordres.
Définition par relation d'ordre
Un treillis est un ensemble E muni d'une relation d'ordre vérifiant :
- pour tous éléments a et b de E, il existe une borne supérieure et une borne inférieure à l'ensemble {a, b}.
Pour munir E d'une structure de treillis algébrique, on remarque que la borne supérieure et la borne inférieure définissent alors deux lois internes :
- ;
- .
Les propriétés de treillis algébrique pour ces deux lois découlent assez directement de la définition.
On définit donc indifféremment les treillis de façon algébrique ou par une relation d'ordre.
Glossaire des treillis
Un ensemble ordonné dans lequel chaque couple d'éléments possède une borne supérieure (ou une borne inférieure) est un demi-treillis.
Un morphisme de demi-treillis de (L, ∨L) vers (M, ∨M) est une application f : L → M telle que pour tous a, b ∈ L, f(a∨Lb) = f(a) ∨M f(b). On dit que c'est un plongement (de demi-treillis) si f est de plus injective. Les définitions d'un morphisme et d'un plongement de treillis vont alors de soi.Exemple : le treillis des partitions d'un ensemble X — isomorphe au treillis des relations d'équivalence sur X — se plonge dans le treillis des sous-groupes du groupe symétrique S(X), en associant à chaque partition π le sous-groupe ∏A∈πS(A).Tout morphisme (resp. tout plongement) de treillis (ou même de demi-treillis) est un morphisme (resp. plongement) d'ensembles ordonnés mais les réciproques sont fausses, et même : tout treillis se plonge dans le treillis des relations d'équivalence sur un certain ensemble[3], qui peut d'ailleurs être choisi fini si le treillis l'est[4].
Un treillis est dit distributif (en) si la loi ⋁ est distributive par rapport à la loi ⋀, ou encore (ce qui dans un treillis est équivalent[5]) si la loi ⋀ est distributive par rapport à la loi ⋁.
Un treillis est dit borné s'il possède un maximum et un minimum. Ainsi l'ensemble des entiers naturels muni de la relation d'ordre ≤ n'est pas borné mais le même ensemble muni de la relation d'ordre « divise » est un treillis borné dont le minimum est 1 et le maximum 0.
Un treillis borné est dit complémenté si chacun de ses éléments x possède un complément y vérifiant x ⋀ y = 0 et x ⋁ y = 1, où 0 désigne l'élément minimum du treillis, et 1 l'élément maximum.
Un treillis distributif borné et complémenté s'appelle aussi une algèbre de Boole.
Un treillis E est dit complet si toute partie de E possède une borne supérieure, ou encore (ce qui est équivalent, voir plus bas) si toute partie de E possède une borne inférieure.
Dans un treillis E possédant un minimum que l'on note 0, les atomes sont les éléments minimaux de E \ {0}. Par exemple dans le treillis de l'ensemble des parties d'un ensemble, les atomes sont les singletons. Certains treillis possédant un minimum peuvent ne pas posséder d'atomes. C'est par exemple le cas de ℝ+, ainsi que de l'ensemble des ouverts réguliers (ouverts égaux à l'intérieur de leur adhérence) d'un espace topologique muni de l'inclusion.
Un idéal du treillis E est une partie non vide I qui est stable par l'opération ⋁ et qui est telle que si x ∈ E et y ∈ I, alors x ⋀ y ∈ I.
Étant donné une partie A d'un ensemble X, l'ensemble des parties de A est un idéal du treillis de l'ensemble des parties de X.
Treillis complet
Dans un treillis, toute partie finie de E possède une borne supérieure et une borne inférieure, mais ce n'est pas toujours le cas pour des parties infinies, même s'il est borné : l'ensemble des rationnels compris entre 0 et 2 est un treillis borné mais il n'est pas complet car l'ensemble des rationnels de cet ensemble dont le carré est inférieur à 2 n'a pas de borne supérieure.
Garrett Birkhoff a introduit le sens suivant de l'épithète « complet » : un ensemble ordonné est dit complet si toute partie admet une borne supérieure (y compris l'ensemble vide, ce qui impose que E ait un minimum). Ceci est équivalent[6] à ce que toute partie possède une borne inférieure (y compris l'ensemble vide, ce qui impose que E ait un maximum).
On dit aussi que E est un espace complètement réticulé. En informatique théorique, le sigle anglais CPO, bien que sa traduction littérale soit « ordre partiel complet », a un sens différent. Pour éviter toute confusion avec une autre notion d'espace complet[7], celle au sens des espaces métriques ou plus généralement des espaces uniformes, Bourbaki avait proposé le terme achevé, qui ne s'est pas imposé. Ainsi, ℝ (qui est complet pour la distance usuelle) n'est pas achevé mais ℝ = ℝ ⋃ {–∞, +∞} l'est, d'où son nom de droite réelle achevée. ℝ est en fait le complété (en) (au sens de Dedekind-MacNeille (en)) de ℝ, c'est-à-dire le plus petit treillis complet contenant ℝ.
Autres exemples.
- Tout segment est un treillis complet.
- L'ensemble des parties d'un ensemble est un treillis complet pour l'inclusion.
- Pour toute partie G d'un treillis complet, le sous-treillis des majorants de G est complet (et de même pour celui des minorants).
- En théorie de l'intégration, si f et g sont deux fonctions boréliennes sur ℝ, intégrables au sens de Lebesgue et vérifiant f < g, l'ensemble des fonctions boréliennes h comprises entre f et g est un treillis non complet qui devient complet si l'on identifie deux fonctions égales presque partout (attention ! la borne supérieure d'une famille de fonctions boréliennes peut être non mesurable ; lorsqu'on quotiente modulo l'égalité presque partout, on regarde ce qu'on appelle une borne essentielle supérieure, laquelle, en revenant aux fonctions, majore presque partout chaque élément de la famille).
Théorème de Knaster-Tarski : toute application croissante d'un treillis complet dans lui-même possède un point fixe.
Dualité
Si est un treillis, alors son treillis dual est .
Principe de dualité : Si un théorème T est vrai pour tous les treillis alors le théorème dual de T, obtenu en remplaçant toutes les occurrences de par (et réciproquement) et toutes les occurrences de par (et réciproquement) est un théorème vrai pour tous les treillis.
Notes et références
- N. Bourbaki, Éléments de mathématique : Théorie des ensembles [détail des éditions], p. ER.28, aperçu sur Google Livres, parle d'« ensemble réticulé, ou réseau ordonné (ou lattis) ».
- En effet, , et de même en intervertissant les deux lois.
- (en) Philip M. Whitman (en), « Lattices, equivalence relations, and subgroups », Bull. Amer. Math. Soc., vol. 52, , p. 507-522 (lire en ligne).
- (en) Pavel Pudlák et Jiří Tůma, « Every finite lattice can be embedded in a finite partition lattice », Algebra Universalis, vol. 10, , p. 74-95 (lire en ligne).
- En effet, si par exemple ⋁ est distributive par rapport à ⋀ alors
- Voir par exemple .
- Voir aussi les pages d'homonymie Complétude
 et Complet
et Complet  .
.
Voir aussi
Articles connexes
Bibliographie
- Ressources disponibles en ligne :
- Garrett Birkhoff, « Théorie et applications des treillis », Annales de l'IHP, vol. 11, no 5, , p. 227-240 (lire en ligne)
- Garrett Birkhoff, « Groupes réticulés », Annales de l'IHP, vol. 11, no 5, , p. 241-250 (lire en ligne)
- (en) Stanley N. Burris et H. P. Sankappanavar, A Course in Universal Algebra, Springer Verlag, 1981 (ISBN 978-3-540-90578-3)
- (en) Peter Jipsen et Henry Rose, Varieties of Lattices, Springer Lecture Notes in Mathematics 1533, 1992 (ISBN 978-0-387-56314-5)
- Ouvrages de référence :
- (en) Thomas Donnellan, Lattice Theory, Pergamon Press, 1968
- (en) G. Grätzer, Lattice Theory: First concepts and distributive lattices, W. H. Freeman, 1971
- (en) B. A. Davey et H. A. Priestley, Introduction to Lattices and Order, Cambridge University Press, 2002
- (en) Garrett Birkhoff, Lattice Theory, AMS Colloquium Publications, vol. 25, 3e éd., 1967















![{\displaystyle (a\land c)\lor (b\land c)=[a\lor (b\land c)]\land [c\lor (b\land c)]=(a\lor b)\land (a\lor c)\land c=(a\lor b)\land c}](https://img.franco.wiki/i/b0d581ac60098e46cd889e1da7e44c0fb2739e7f.svg)