Tests de l'énergie et de la quantité de mouvement relativistes
Les tests de l'énergie et de la quantité de mouvement relativistes visent à confirmer les expressions relativistes de l'énergie, de la quantité de mouvement et de la masse. Selon la relativité restreinte, certaines propriétés de particules élémentairess massives qui atteignent des vitesses proches de la vitesse de la lumière dévient de façon significative des prédictions de la mécanique newtonienne. Par exemple, aucune particule massive ne peut atteindre la vitesse de la lumière.
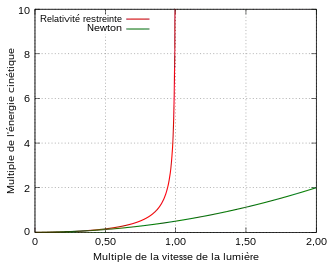
Au XXIe siècle, ces expressions relativistes pour des particules voyageant à une vitesse proche de la lumière sont régulièrement confirmées dans des laboratoires universitaires. Elles servent à la conception et à la mise au point d'accélérateurs de particules.
Aperçu

En mécanique newtonienne, l'énergie cinétique et la quantité de mouvement sont calculées à l'aide de
La relativité restreinte postule que la vitesse de la lumière dans le vide est constante et ultime, peu importe le référentiel inertiel. Pour cette raison, la relation relativiste énergie–quantité de mouvement est donnée par :
- ,
où l'énergie relativiste , l'énergie cinétique et la quantité de mouvement d'une particule massive sont données par :
- ,
où .
Donc, l'énergie et la quantité de mouvement relativistes augmentent de façon notable avec la vitesse d'une particule massive, qui ne peut excéder la vitesse de la lumière.
Par ailleurs, si la vitesse est nulle, alors et . Cette énergie au repos est donc :
- ,
Premières expériences
Les premières expériences pouvant déterminer si de telles relations sont vraies ont été conduites par Walter Kaufmann, Alfred Bucherer et Carl Neumann entre 1901 et 1915. Elles ont principalement portées sur la déflexion de rayons bêta soumis à un champ magnétique dans le but de déterminer le rapport masse sur charge de l'électron. En effet, les scientifiques savaient que la charge électrique est indépendante de la vitesse de cette particule ; toute variation pourrait alors être attribuée à une modification de la quantité de mouvement ou à la masse (qui était connue à cette époque comme la masse électromagnétique (en) transverse , équivalente à la masse relativiste mentionnée plus haut). Ces tests servent à valider l'énergie et la quantité de mouvement relativistes, puisque la relation suivante s'applique :
Les expérimentateurs ont observé des électrons se déplaçant à une vitesse entre 0,25c et 0,75c. Ils ont établi que leur quantité de mouvement augmentait en accord avec les prédictions de la relativité restreinte, ce qui a été considéré comme une confirmation de la validité de la théorie. La précision atteinte ne pouvait cependant pas éliminer d'autre théories, telle celle proposée par Max Abraham[1] - [2].
En 1915, Arnold Sommerfeld détermine la structure fine du spectre de l'hydrogène en utilisant les formules relativistes de l'énergie et de la quantité de mouvement (dans le contexte de la théorie Bohr–Sommerfeld). Par la suite, Karl Glitscher (en) remplace les formules relativistes par celles d'Abraham, ce qui invalide sa théorie[3].
Des mesures de plus en plus précises
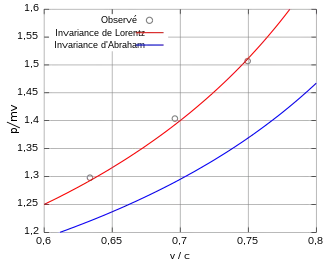
En 1940, Rogers et al. font défléchir des électrons en s'inspirant des expériences de Kaufmann–Bucherer–Neumann, dont ils ont amélioré plusieurs aspects. Ils ont mesuré la vitesse et le rapport masse à la charge électrique de particules bêta pour des vitesses allant jusqu'à 0,75c. La précision atteinte permet de confirmer les prédictions de la relativité restreinte à une erreur de moins de 1 %[4]. Cette précision permet d'éliminer des théories en compétition avec la relativité restreinte.
Une mesure plus précise de la déflexion d'électrons a été réalisée par Meyer et al. en 1963. Ils ont observé des électrons se déplaçant à une vitesse comprise entre 0,987c et 0,9c, électrons défléchis dans un champ magnétique statique homogène où p a été mesuré et dans un champ électrique statique cylindrique où a été mesuré. Ils ont confirmé les prédictions de la relativité restreinte avec une erreur inférieure à ∼0,000 37[5].
Également, Grove et Fox ont obtenu en 1953 des protons se déplaçant à ∼0,7c. Ils ont déterminé la fréquence angulaire et le champ magnétique, ce qui leur a permis de calculer le rapport charge à la masse (et donc la quantité de mouvement) du proton. Ils ont validé l'expression relativiste de ce rapport à une précision de ∼0,000 6[6].
Néanmoins, Zrelov et al. (1958) ont critiqué le manque d'information de l'expérience de Grove et Fox, mettant l'emphase sur la difficulté d'effectuer de telles mesures à cause du mouvement complexe des protons. Ils ont donc conduit une expérience plus élaborée où des protons se déplaçant à une vitesse moyenne de 0,8112c ont été observés. La quantité de mouvement a été calculée avec un fil de Litz et la vitesse a été évaluée grâce au rayonnement Tcherenkov. Ils ont confirmé les prédictions de la relativité restreinte à une précision inférieure à ∼0,004 1[7].
Expérience de Bertozzi
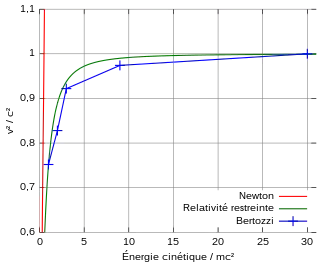
Depuis les années 1930, la relativité restreinte est nécessaire pour concevoir des accélérateurs de particules. Même si la théorie a été confirmée par les expériences citées plus haut, c'était de façon indirecte puisque les expérimentateurs devaient tenir compte de plusieurs facteurs : courbes de déflexion, vitesse des particules et quantités de mouvement.
William Bertozzi, en 1962 et en 1964, mène une série d'expériences visant à déterminer les effets relativistes de façon directe. Il emploie un accélérateur d'électrons du MIT qui effectue cinq jets d'électrons d'énergies différentes entre 0,5 et 15 MeV. Chaque jet est créé à l'aide d'un générateur de Van de Graaff : les électrons voyagent sur 8,4 m jusqu'à ce qu'ils frappent un disque en aluminium. Le temps de vol de chaque jet est mesuré – la vitesse atteinte est en proche accord avec les prédictions de la relativité restreinte. Néanmoins, l'énergie cinétique est déterminée indirectement à l'aide de l'énergie dégagée par les champs d'accélération. Bertozzi mesure alors l'élévation de température causée par les collisions des électrons contre le disque. Il obtient des énergies cinétiques qui sont en accord à 10 % près des prédictions relativistes[8] - [9].
Expériences en milieu universitaire
À cause de leur simplicité relative, que ce soit les calculs ou le matériel nécessaire, plusieurs expériences ont été réalisées en milieu universitaire. La masse, la vitesse, la quantité de mouvement et l'énergie d'électrons ont été mesurées de différentes façons dans le cadre de ces expériences, qui ont toutes confirmées les prédictions de la relativité restreinte[10]. Ont été utilisés des particules bêtas, la diffusion Compton (où les électrons présentent de fortes caractéristiques relativistes) et l'annihilation électron-positron.
Accélérateurs de particules
Dans les accélérateurs de particules de hautes énergies modernes, les prédictions de la relativité restreinte sont régulièrement confirmées, tout en étant nécessaires pour la conception et l'évaluation théorique des expériences, particulièrement aux limites ultra-relativistes[22] - [note 1]. Par exemple, la dilatation du temps est nécessaire pour expliquer le temps de désintégration d'une particule. Le théorème d'addition des vitesses relativistes (en) explique la distribution du rayonnement synchrotron. À propos de la relation relativiste énergie—quantité de mouvement, une série d'expériences de haute précision visant à mesurer la vitesse et le relation énergie—quantité de mouvement a été conduite : les énergies atteintes ont été plus élevées que dans les expériences précédemment mentionnées[24].
Vitesses
Alväger et al. (1964) au Proton Synchrotron du CERN ont mesuré les temps de vol dans le but de valider la formule de la quantité de mouvement newtonienne de la lumière selon la théorie de l'émission. Dans cette expérience, des rayons gamma ont été produits à partir de la désintégration de Pions de 6 GeV qui voyageaient à 0,99975c. Si la quantité de mouvement newtonienne avait été valide, ces rayons auraient dû se déplacer à des vitesses supraluminiques. Les vitesses ont toujours été inférieure à la vitesse de la lumière[25].
Des expériences portant sur les temps de vol ont été faites dans le but de mesurer les différences entre les vitesses d'électrons et de la lumière au Centre de l'accélérateur linéaire de Stanford (SLAC). Par exemple, Brown et al. (1973) n'ont trouvé aucune différence significative entre le temps de vol d'électrons d'une énergie de 11 GeV et celui de la lumière visible, calculant une différence maximale de vitesses de [26]. Une autre expérience au SLAC menée par Guiragossián et al. (1974) a accéléré des électrons jusqu'à des énergies comprises entre 15 et 20,5 GeV. Utilisant un séparateur de fréquences radios pour mesurer les différences des temps de vol et donc les différences de vitesses entre ces électrons et des rayons gamma de 15 GeV sur une trajectoire de 1 015 m, ils n'ont découvert aucune différence significative, donnant une différence maximale de [27].
Énergie et calorimétrie
L'intrusion de particules dans les détecteurs de particules est une conséquence de l'annihilation électron-positron, de la diffusion Compton, du rayonnement de Tcherenkov, etc. Ensemble, ils provoquent la création de nouvelles particules (photons, électrons, neutrinos, etc.). Les énergies de ces pluies de particules correspondent aux énergies cinétiques relativistes et aux énergies de repos des particules qui leur ont donné naissance. Elles peuvent être mesurées par des calorimètres conçus à cet effet, que ce soit de façon électrique, optique, thermique ou acoustique[28].
Dans le but d'établir l'énergie cinétique relativiste, des mesures thermiques ont été réalisées par Bertozzi dans les années 1960 tel que mentionné plus haut. Des mesures au SLAC ont été faites plus tard, en 1982, où l'énergie thermique d'électrons de 20 GeV a été mesurée. Doté d'instruments pertinents, un bloc d'aluminium refroidi à l'eau a servi comme calorimètre. Les résultats obtenus concordent avec les prédictions de la relativité restreinte, à une précision de 30 %[29]. Néanmoins, les expérimentateurs ont fait allusion à une expérience antérieure où des mesures calorimétriques avec des électrons à 10 GeV ont été faites en 1969. L'usage d'un bloc de cuivre a permis d'atteindre une précision de 1 %[30].
Dans les calorimètres modernes, qu'ils soient électromagnétiques ou hadroniques, les énergies des pluies de particules sont régulièrement mesurées en observant l'ionisation qu'elles ont causées. Également, des excitations peuvent être mesurées par des détecteurs à scintillation. Peu importe la méthode, la mesure est toujours proportionnelle à l'énergie de la particule qui a donné naissance à la pluie de particules[28].
Annihilations et créations de paires
L'énergie et la quantité de mouvement relativistes peuvent aussi être mesurées en étudiant des processus physiques, telles l'annihilation et la création de paires[31]. Par exemple, les énergies au repos des électrons et des positrons sont identiques, soit 0,51 MeV. Quand un photon interagit avec un noyau atomique, des paires électron-positron peuvent être créées si l'énergie du photon égale l'énergie de seuil, qui est dans ce cas . Si l'énergie du photon est plus élevée, l'énergie excédentaire est convertie en énergie cinétique consommée par les particules créées. Le processus inverse, l'annihilation électron-positron, est observé pour de faibles énergies. Des photons sont créés ; ils ont la même énergie que la paire électron-positron qui leur a donnée naissance. Il s'agit d'exemples directs de (équivalence masse-énergie).
Les scientifiques ont documenté plusieurs exemples de conversions d'énergie cinétique relativiste en énergie au repos (donc, une partie de l'énergie cinétique a été convertie en masse). En 1974, le SLAC a accéléré des électrons et des positrons à de très grandes vitesses de façon que leur énergie relativiste (c'est-à-dire la somme de leur énergie au repos et de leur énergie cinétique) soit d'environ 1 500 MeV chacun. Lorsque des électrons accélérés ont percuté des positrons accélérés, leur collision a créé des particules de plus grandes énergie, notamment des mésons J/ψ d'une énergie au repos d'environ 3 000 MeV[32]. Des expériences avec des énergies encore plus élevées ont été réalisées au Grand collisionneur électron-positron en 1989 : des électrons et des positrons ont été chacun accélérés à des énergies pouvant atteindre 45 GeV, dans le but de produire des bosons W et Z d'énergies au repos se situant entre 80 et 91 GeV. Plus tard, les niveaux d'énergie ont atteint 200 GeV, dans le but de générer des paires de bosons W[33]. Les énergies de ces bosons peuvent aussi être mesurée à l'aide d'annihilations protons-antiprotons. L'énergie combinée de ces deux particules est d'environ 0,938 GeV. Le Super Proton Synchrotron a accéléré ces particules à de très grandes vitesses, leur impulsant une énergie d'environ 270 GeV chacun. Lors de collisions, l'énergie disponible était donc d'environ 540 GeV. En conséquence, les quarks et les antiquarks ont pu accumuler suffisamment d'énergie et de quantité de mouvement pour s'annihiler en bosons W et Z[34].
Plusieurs autres expériences engageant des énergies encore plus élevées ont été menées, qui ont toutes confirmées les prédictions de la relativité restreinte avec une faible marge d'erreur. Par exemple, le Tevatron a pu atteindre 1 TeV, le Relativistic Heavy Ion Collider peut atteindre 200 GeV. Plus récemment, le Large Hadron Collider a pu atteindre 7 TeV, à la recherche du boson de Higgs.
Notes et références
(en) Cet article est partiellement ou en totalité issu de la page de Wikipédia en anglais intitulée « Tests of relativistic energy and momentum » (voir la liste des auteurs).
Notes
- Ces limites sont atteintes lorsque dans . C'est également le cas lorsque dans [23].
Références
- (en) Zahn, C. T. et Spees, A. A., « A Critical Analysis of the Classical Experiments on the Variation of Electron Mass », Physical Review, vol. 53, no 7, , p. 511–521 (DOI 10.1103/PhysRev.53.511, Bibcode 1938PhRv...53..511Z)
- (en) P. S. Faragó et L. Jánossy, « Review of the experimental evidence for the law of variation of the electron mass with velocity », Il Nuovo Cimento, vol. 5, no 6, , p. 379–383 (DOI 10.1007/BF02856033, Bibcode 1957NCim....5.1411F, S2CID 121179531)
- (en) Glitscher, Karl, « Spektroskopischer Vergleich zwischen den Theorien des starren und des deformierbaren Elektrons », Annalen der Physik, vol. 357, no 6, , p. 608–630 (DOI 10.1002/andp.19173570603, Bibcode 1917AnP...357..608G, hdl 2027/uc1.b2637473, lire en ligne)
- (en) Marguerite M. Rogers, A. W. McReynolds et F. T. Rogers, « A Determination of the Masses and Velocities of Three Radium B Beta-Particles: The Relativistic Mass of the Electron », Physical Review, vol. 57, no 5, , p. 379–383 (DOI 10.1103/PhysRev.57.379, Bibcode 1940PhRv...57..379R, hdl 1911/18426)
- (en) V. Meyer, W. Reichart et H. H. Staub, « Experimentelle Untersuchung der Massen-Impulsrelation des Elektrons », Helvetica Physica Acta, vol. 36, , p. 981–992 (DOI 10.5169/seals-113412)
- (en) D. J. Grove et J. C. Fox, « e/m for 385-MeV protons (UA7) », Physical Review, vol. 90, no 2, , p. 378 (DOI 10.1103/PhysRev.90.333, Bibcode 1953PhRv...90..333.)
- (en) V. P. Zrelov, A. A. Tiapkin et P. S. Farago, « Measurement of the mass of 600 MeV protons », Soviet Physics JETP, vol. 7, no 3, , p. 384–387
- (en) William Bertozzi, « Speed and Kinetic Energy of Relativistic Electrons », American Journal of Physics, vol. 32, no 7, , p. 551-555 (DOI 10.1119/1.1970770, Bibcode 1964AmJPh..32..551B)
- (en) William Bertozzi, « The Ultimate Speed - An Exploration with High Energy Electrons » [vidéo],
- (en) Robert E. Marvel et Michael F. Vineyard, « Relativistic Electron Experiment for the Undergraduate Laboratory »,
- (en) M. Lund et U. I. Uggerhøj, « Experimental special relativity with a meter stick and a clock », American Journal of Physics, vol. 77, no 8, , p. 757–761 (DOI 10.1119/1.3049532, Bibcode 2009AmJPh..77..757L)
- (en) John W. Luetzelschwab, « Apparatus to measure relativistic mass increase », American Journal of Physics, vol. 71, no 8, , p. 878–884 (DOI 10.1119/1.1561457, Bibcode 2003AmJPh..71..878L)
- (en) Jack G. Couch et Terry K. Dorries, « Measuring relativistic electrons in the undergraduate laboratory », American Journal of Physics, vol. 50, no 10, , p. 917–921 (DOI 10.1119/1.12973, Bibcode 1982AmJPh..50..917C)
- (en) Kenneth N. Geller et Richard Kollarits, « Experiment to Measure the Increase in Electron Mass with Velocity », American Journal of Physics, vol. 40, no 8, , p. 1125–1130 (DOI 10.1119/1.1986771, Bibcode 1972AmJPh..40.1125G)
- (en) Sherwood Parker, « Relativity in an Undergraduate Laboratory-Measuring the Relativistic Mass Increase », American Journal of Physics, vol. 40, no 2, , p. 241–244 (DOI 10.1119/1.1986498, Bibcode 1972AmJPh..40..241P)
- (en) A. A. Bartlett et Malcolm Correll, « An Undergraduate Laboratory Apparatus for Measuring e/m as a Function of Velocity. I », American Journal of Physics, vol. 33, no 4, , p. 327–339 (DOI 10.1119/1.1971493, Bibcode 1965AmJPh..33..327B)
- (en) P. L. Jolivette et N. Rouze, « Compton scattering, the electron mass, and relativity: A laboratory experiment », American Journal of Physics, vol. 62, no 3, , p. 266–271 (DOI 10.1119/1.17611, Bibcode 1994AmJPh..62..266J)
- (en) Matthiam J. H. Hoffman, « The Compton effect as an experimental approach toward relativistic mass », American Journal of Physics, vol. 57, no 9, , p. 822–825 (DOI 10.1119/1.15902, Bibcode 1989AmJPh..57..822H)
- (en) P. A. Egelstaff, J. A. Jackman, P. J. Schultz, B. G. Nickel et I. K. MacKenzie, « Experiments in special relativity using Compton scattering of gamma rays », American Journal of Physics, vol. 49, no 1, , p. 43–47 (DOI 10.1119/1.12659, Bibcode 1981AmJPh..49...43E)
- (en) J. Higbie, « Undergraduate Relativity Experiment », American Journal of Physics, vol. 42, no 8, , p. 642–644 (DOI 10.1119/1.1987800, Bibcode 1974AmJPh..42..642H)
- (en) Jerzy Dryzek, Douglas Singleton, Suzuki, Takenori et Yu, Runsheng, « An undergraduate experiment to test relativistic kinematics using in flight positron annihilation », American Journal of Physics, vol. 74, no 1, , p. 49–53 (DOI 10.1119/1.2142624, Bibcode 2006AmJPh..74...49D)
- (en) Tomas Plettner, Robert L. Byer et Siemann, Robert H., « The impact of Einstein's theory of special relativity on particle accelerators », Journal of Physics B, vol. 38, no 9, , S741–S752 (DOI 10.1088/0953-4075/38/9/020, Bibcode 2005JPhB...38S.741P)
- (en) M. E. Dieckmann, « Particle simulation of an ultrarelativistic two-stream instability », Phys. Rev. Lett., vol. 94, no 15, , p. 155001 (PMID 15904153, DOI 10.1103/PhysRevLett.94.155001, Bibcode 2005PhRvL..94o5001D)
- (en) Yuan Zhong Zhang, Special Relativity and Its Experimental Foundations, World Scientific, (ISBN 978-981-02-2749-4, lire en ligne
 )
) - (en) T. Alväger, F. J. M. Farley, J. Kjellman et L. Wallin, « Test of the second postulate of special relativity in the GeV region », Physics Letters, vol. 12, no 3, , p. 260-262 (DOI 10.1016/0031-9163(64)91095-9, Bibcode 1964PhL....12..260A)
- (en) B. C. Brown, G. E. Masek, T. Maung, E. S. Miller, H. Ruderman et W. Vernon, « Experimental Comparison of the Velocities of eV (Visible) and GeV Electromagnetic Radiation », Physical Review Letters, vol. 30, no 16, , p. 763-766 (DOI 10.1103/PhysRevLett.30.763, Bibcode 1973PhRvL..30..763B)
- (en) Z. G. T. Guiragossián, G. B. Rothbart, M. R. Yearian, R. A. Gearhart et J. J. Murray, « Relative Velocity Measurements of Electrons and Gamma Rays at 15 GeV », Physical Review Letters, vol. 34, no 6, , p. 335-338 (DOI 10.1103/PhysRevLett.34.335, Bibcode 1975PhRvL..34..335G)
- (en) Christian W. Fabjan, et Fabiola Gianotti,, « Calorimetry for particle physics », Reviews of Modern Physics, vol. 75, no 4, , p. 1243-1286 (DOI 10.1103/RevModPhys.75.1243, Bibcode 2003RvMP...75.1243F, lire en ligne [PDF])
- (en) Dieter R. Walz, H. Pierre Noyes et Ricardo L. Carezani, « Calorimetric test of special relativity », Physical Review A, vol. 29, no 4, , p. 2110–2113 (DOI 10.1103/PhysRevA.29.2110, Bibcode 1984PhRvA..29.2110W)
- (en) G. E. Fischer et Y. Murata, « A beam monitor system for high-intensity photon beams in the multi-GeV range », Nuclear Instruments and Methods, vol. 78, no 1, , p. 25-39 (DOI 10.1016/0029-554X(70)90425-8, Bibcode 1970NucIM..78...25F)
- (en) Edwin F. Taylor et John Archibald Wheeler, Spacetime Physics: Introduction to Special Relativity, New York, W. H. Freeman, (ISBN 0-7167-2327-1, lire en ligne
 )
) - (en) Burton Richter, « From the Psi to Charm – The Experiments of 1975 and 1976 », Nobel lecture 1976,
- (en) LEP collaborations, « Electroweak parameters of the Z0 resonance and the standard model », Physics Letters B, vol. 276, no 12, , p. 247–253 (DOI 10.1016/0370-2693(92)90572-L, Bibcode 1992PhLB..276..247., hdl 2066/124399)
- (en) Carlo Rubbia, « Experimental Observation of the Intermediate Vector Bosons W+, W- and Z0 », Nobel lecture 1984,
Liens externes
- (en) Liste de tests de la relativité restreinte sur Physics FAQ























