Temps de réverbération
En acoustique architecturale, on appelle réverbération la prolongation d'un son après l'interruption de la source sonore, du fait des multiples réflexions sur les parois d'un local. Le temps de réverbération d'un local est le temps nécessaire pour que la pression acoustique diminue à un millième de sa valeur initiale. Ce rapport de pression correspond à une diminution de niveau de 60 décibels.
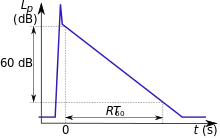
Le temps de réverbération, noté T60, T ou bien TR ou RT (pour Reverberation Time, en anglais), est la caractéristique la plus citée pour les salles où l'on se préoccupe d'acoustique.
Les normes d'évaluation acoustique précisent qu'on peut donner le temps de réverbération d'une salle par bande de fréquence, soit d'une octave, soit d'un tiers d'octave, ou bien globalement pour toutes les fréquences audibles.
Mesure
L'acousticien Wallace Sabine a entrepris peu avant 1900 les premières études sur la réverbération, avec des mesures dans des salles existantes et l'établissement d'un modèle basé sur les lois de propagation du son. Ne disposant d'aucun instrument de mesure du niveau sonore, Sabine effectuait ses évaluations avec un chronomètre déclenché à la fin du son d'excitation et arrêté par lui-même quand la réverbération devenait inaudible. Quand, cinquante ans plus tard, les instruments ont été disponibles, on a recherché une définition plus rigoureuse qui donne des résultats proches, et on a normalisé une décroissance au millième de la pression acoustique.
Avec des instruments électroniques, on se rend compte que la réverbération n'est pas uniforme. Elle se compose, après l'interruption du son direct, d'une phase de premières réflexions où le niveau sonore est désordonné, pour finir par une décroissance exponentielle de la pression acoustique, dont la pente en décibels par seconde est linéaire. Les premières réflexions dépendent de la position du point d'excitation, de celle du point de mesure, et typiquement varient à chaque mesure[1]. La partie régulière de la décroissance, correspondant à un champ sonore parfaitement diffus, dépend moins des positions d'excitation et de mesure. Le rapport entre les deux parties dépend d'une caractéristique des parois appelée diffusion. Plus les parois sont diffusantes, plus la puissance sonore réfléchie s'éparpille dans toutes les directions, et plus rapidement on arrive à une décroissance régulière du niveau sonore.
La mesure du temps de réverbération peut se faire au moyen d'une source sonore excitatrice ou d'une impulsion sonore (ex. : pistolet d'alarme).
Un son d'excitation doit, avant d'être interrompu, persister suffisamment longtemps pour que le niveau sonore arrive en régime stable, soit une durée approximativement égale au temps de réverbération[2]. Ce niveau peut servir de référence, et le temps nécessaire pour que le son décroisse de 60 dB est le temps de réverbération.
Avec une impulsion sonore, on ne peut pas mesurer le niveau d'excitation. Pendant la phase des premières réflexions, il fluctue, et il faut attendre la décroissance régulière pour en déterminer la pente en décibels par seconde. On convertit ensuite en secondes pour 60 dB, même si la partie mesurable de cette décroissance est largement moindre. Alternativement, on peut appliquer la méthode de Schroeder (en), en intégrant un enregistrement de la décroissance à l'envers, en partant de la fin. On obtient une courbe plus régulière, qui permet de détecter la présence d'un taux de décroissance variable, qui témoigne de problèmes de résonance acoustique[3].
Les trois méthodes donnent rarement le même résultat, mais la différence dépasse rarement un rapport de un à un et demi.
Les normes ISO 3382-1:2009 pour les salles de spectacles et ISO 3382-2:2008 pour les salles ordinaires régissent la mesure du temps de réverbération.
Modélisation
Le temps de réverbération dépend[4] :
- de la forme de la salle ;
- du volume de la salle ;
- du coefficient d'absorption acoustique du matériau des parois, qui dépend en général de la fréquence[5] ;
- de la vitesse du son.
Formules de Sabine et de Eyring
Sabine a établi en 1898 la relation fondamentale entre le volume d'une salle, les propriétés d'absorption acoustique des surfaces de ses parois et le temps de réverbération. Il construisit un modèle théorique où chaque élément de paroi est doté d'un coefficient d'absorption exprimant la part de l'énergie sonore absorbée par le matériau[4] et où le champ sonore est idéalement diffus, c'est-à-dire que la probabilité des ondes sonores soient la même dans toutes les directions. Dans ces conditions, utilisant un modèle d'acoustique géométrique statistique, il calcula le libre parcours moyen entre deux réflexions, et de là, avec la vitesse du son en paramètre, il montra que le temps de réverbération T pour la salle entière est proportionnel à son volume V et inversement proportionnel à l'aire d'absorption équivalente A (k est une constante de proportionnalité).
- où k≈ 0,163
avec :
- où α est le coefficient d'absorption et m l'amortissement du milieu (par exemple l'air).
Le calcul avec la formule de Sabine consiste à diviser les parois en i éléments de surface Si. Il faut, pour chaque élément, trouver les caractéristiques d'absorption (αi) du matériau, soit dans des répertoires, soit en procédant à des essais. On calcule ensuite la moyenne des coefficients pondérée par la surface, de préférence bande de fréquence par bande de fréquence.
La formule de Sabine est valable tant que α est sensiblement inférieur à 1. Avec le même modèle théorique, pour des valeurs de α plus grandes qu'environ 0,3, la formule de Eyring fournit de meilleurs résultats[6]. Celle-ci, précisée dans les années 1920 et utilisée lors la conception acoustique de bâtiments durant leur phase de construction, est valable pour n'importe quel α :
- .
Pour de faibles valeurs de α, l'approximation ramène à l'équation de Sabine.
Ces calculs d'acoustique architecturale sont fondés sur un modèle de salle dont toutes les dimensions sont du même ordre de grandeur. L'intensité acoustique diminue proportionnellement au carré de la distance à la source, et chaque réflexion absorbe une partie de l'énergie. Les équations intègrent les distances et le nombre de réflexions pour toutes les ondes sonores. L'acoustique des couloirs et tunnels ne peut utiliser ces formules.
Plus le volume de la salle est grand et plus les matériaux composant la salle sont réfléchissants, plus le temps de réverbération sera long.
Dans les deux formules, la constante de proportionnalité k a pour valeur :
- .
Le terme d'amortissement peut être négligé surtout dans le cas de petites salles.
Ces modèles fondés sur l'hypothèse d'un champ diffus supposent une salle grande par rapport aux longueurs d'onde en jeu. Schroeder a défini une fréquence au-dessus de laquelle une salle peut présenter un champ suffisamment diffus[7] :
- où T est le temps de réverbération et V le volume.
Cette formule permet de déterminer le volume minimal pour que le champ puisse être suffisamment diffus à une fréquence donnée, avec le champ de réverbération en paramètre.
La fréquence fondamentale correspondant à la note do de la deuxième octave est légèrement supérieure à 130 Hz. Le volume minimal d'une salle dont le temps de réverbération serait de 1,4 s pour que les réverbérations de cette note puissent constituer un champ diffus sont, d'après la formule de Schroeder :
- .
Modèle itératif
Les modèles de Sabine et celui de Eyring aboutissent à la conclusion que le temps de réverbération est uniforme dans un même local, et que l'emplacement des surfaces absorbantes, diffusantes et réfléchissantes n'a pas d'influence. L'expérience montre, au contraire, que la mesure du temps de réverbération varie quelque peu selon l'emplacement de la source et du microphone de mesure, et selon la méthode de mesure[8]. C'est que ce modèle implique que les parois soient idéalement diffusantes[9], ce qui n'est pas le cas en général. Les divergences, cependant, n'affectent pas l'ordre de grandeur du temps de réverbération.
La possibilité ouverte à partir des années 1960 d'explorer pas à pas, sur ordinateur, des modèles géométriques de salles a montré que le modèle de Sabine et de Eyring peut diverger assez considérablement de la réalité. On suit l'évolution de rayons sonores lancés dans une direction au hasard. Ces calculs ont confirmé un fait d'expérience, qui contredisait le modèle : la position des éléments de paroi réfléchissants, absorbants et diffusants influe sur le temps de réverbération, et non seulement leur surface globale. La différence de temps de réverbération peut atteindre 60 % selon le placement de certains éléments[10].
Ces modèles impliquent un travail de codification des données de la salle considérablement plus important que pour ceux de Sabine et de Eyring, qui constituent toujours une première approximation.
Temps de réverbération optimal
Le temps de réverbération optimal dépend du volume de la salle et de l'usage qui doit en être fait[11]. La musique demande un temps de réverbération plus long. Les acteurs, conférenciers et musiciens sur scène ont besoin d'une réverbération minimale ; mais la réverbération augmente aussi le niveau sonore provenant de sources indésirables (machines, sonorisation, conversations).
Formule de Stephen et Bate
Pour des salles de proportions identiques, et dont les parois sont constituées de matériaux de même absorption moyenne, des études statistiques réalisées par Stephen et Bate (1950) ont montré que le temps de réverbération optimal de quatre types de salles occupées est proportionnel à la racine cubique du volume V[12] :
- où a est une constante qui vaut 4 pour le langage parlé, 4,5 pour l'opéra, 5 pour les orchestres et 6 pour les chœurs.
Ordres de grandeur, valeurs typiques et anecdotes
Le T typique d'un studio d'enregistrement est de 0,3 s[4].
Les ordres de grandeur de temps de réverbération sont de 0,5 s pour une pièce meublée, de 2 à 4 s pour une pièce vide, de 8 à 12 s pour un grand hall[13].
Pour un hall ou un quai de gare, la valeur est entre 1,5 et 3 s[11].
Le T d'une salle de conférence de 500 m3 peut être réglé à 1 s[13].
Le T de la salle principale de l'Opéra Bastille (volume 21 000 m3) vaut 1,7 s à vide et 1,5 s occupée. En effet, l'aire d'absorption équivalente d'une personne assise vaut par exemple 0,50 m2 à 1 000 Hz (et 0,20 m2 à 125 Hz)[14].
Dans une nef de cathédrale, T peut atteindre une dizaine de secondes.
Dans les grandes chambres réverbérantes, les T peuvent être de l'ordre de 30 à 40 s[13].
Anecdotes :
- une cage d'escalier en béton (matériau très rigide et réfléchissant) présente un T élevé et peu de parois parallèles, donnant peu de résonances modales ; ses propriétés acoustiques se rapprochent ainsi de celles d'une chambre réverbérante. Un ingénieur du son peut parfois exploiter cette « chambre de réverbération » improvisée[15] ;
- en 2014, Trevor Cox (en) fait inscrire au Livre Guinness des records la valeur de 112 s, mesurée à 125 Hz dans une galerie souterraine de stockage d'hydrocarbure désaffectée de 210 m de long construite en Écosse[16].
Applications
Bureaux paysagers
La maîtrise acoustique dans un bureau paysager est essentielle. Il est reconnu qu’un temps de réverbération de moins de 0,5 s convient pour un open space (0,5 s est le temps préconisé dans la norme suédoise SS 02 52 68. La norme française NF S 31-080 considère des temps de réverbérations différents selon les types d'espaces et les niveaux de performances attendus. Lorsque le volume du local est supérieur à 250 mètres cubes il est conseillé d'utiliser le critère de décroissance sonore spatiale). Un temps de réverbération modéré assure une bonne intelligibilité de la parole, ce qui assure le confort d’écoute.
Dans un open space, on ne peut pas empêcher quelqu’un de parler, mais on peut empêcher que le son de sa voix ne porte à plus de 10 m : c’est le rôle des éléments de correction acoustique (plafonds, panneaux muraux, claustras, …).
Salle d'écoute domestique
Dans une salle de séjour destinée à l’écoute de musique Hi-Fi, le temps de réverbération ne doit pas excéder quelques dixièmes de seconde[14]. Dans le cas contraire, la salle est trop réverbérante et elle nécessite un traitement acoustique. Par exemple, la mise en place de panneaux muraux rigides composés de matériaux absorbants (laine minérale de verre ou de roche, mousse synthétique à structure ouverte, fibres de bois compressées, etc.) diminue la réverbération du local. Le son réfléchi est atténué, ce qui permet une écoute neutre et précise.
Voir aussi
Articles connexes
Liens externes
- Norme ISO 3382-1:2009 : Acoustique — Mesurage des paramètres acoustiques des salles — Partie 1 : Salles de spectacles
- Norme ISO 3382-2:2008 : Acoustique — Mesurage des paramètres acoustiques des salles — Partie 2 : Durée de réverbération des salles ordinaires
- Norme ISO 11654:1997 : Acoustique — Absorbants pour l'utilisation dans les bâtiments — Évaluation de l'absorption acoustique
- Norme NF S 31-080 : Acoustique — Bureaux et espaces associés
Bibliographie
- Éric Vivié et Michel Cassan, « Acoustique Architecturale », dans Denis Mercier (direction), Le Livre des Techniques du Son, t. 1 - Notions fondamentales, Paris, Eyrolles, , 1re éd. (présentation en ligne)
- Antonio Fischetti, Initiation à l'acoustique, Paris, Belin, .
- Mario Rossi, Audio, Lausanne, Presses polytechniques et universitaires romandes, , 1re éd., p. 207-237, chap. 3, Acoustique statistique, §4 Acoustique statistique.
Notes et références
- (en) Manfred R. Schroeder, « A new method of Measuring Reverberation Time », J. Acoust. Soc. Am., vol. 37, no 409, .
- Fischetti 2001, p. 108.
- Schroeder 1965.
- (en) R.C. Jaiswal, Audio-Video Engineering, Bombay, Nirali Prakashan, , 3e éd. (ISBN 978-81-906396-7-5, lire en ligne), p. 6.7-6.8
- En absorption acoustique, le spectre d'absorption (typiquement de 125 à 4 000 Hz) d'un matériau permet d'évaluer son efficacité ; il existe 5 classes d'absorption, de « A » (la plus grande absorption acoustique) à « E ».
- (en) Carl F. Eyring, « Reverberation time in “dead” rooms », J. Acoust. Soc. Am., vol. 1, no 2A, , p. 217-241 ; Rossi 2007, p. 211
- Rossi 2007, p. 213.
- J.P. R. Flenner, J.P. Guilhot et C. Legros, « Dispersion des mesures de la durée de réverbération d'un local », Acta Acustica, vol. 50, no 3, , p. 201-208 résumé en ligne.
- (en) H. Kutruff, Room Acoustics, Londres, Spon Press, , apud Rossi 2007, p. 211
- (en) Manfred R. Schroeder et D. Hackman, « Iterative Calculation of Reverberation Time », Acta Acustica, vol. 45, no 4, , p. 269-273 résumé en ligne.
- Ricardo Atienza et Suzel Balez, Acoustique des salles, (lire en ligne), p. 26.
- (en) David A. Bies et Colin H. Hansen, Engineering Noise Control : Theory and Practice, CRC Press, , 4e éd., 748 p. (ISBN 978-0-203-87240-6 et 0-203-87240-1, lire en ligne), p. 345
- Claude Lesueur, Acoustique, chap. 4 : Champ acoustique dans les cavités : approche modale, par champ diffus et acoustique géométrique, 1997 (polycopié).
- Jean-Pierre Morand, « Traitement acoustique - Acoustique et écoute domestique », Revue du son et du home cinéma, no 252, , p. 96-100
- (en) Glenn D. White et Gary J. Louie, The Audio Dictionary, Seattle, University of Washington Press, , 3e éd., 504 p. (ISBN 0-295-98498-8, lire en ligne), p. 331
- (en) Université de Salford, « News - Salford professor discovers world’s longest echo », sur staff.salford.ac.uk, (consulté le ).








![{\displaystyle T_{\mathrm {opt} }=a[0,0118\ V^{\frac {1}{3}}+0,1070]}](https://img.franco.wiki/i/a3d62f6a94f52c381ae21c46ddd7ee6da82de29f.svg)